Интегральные представления решений уравнений Максвелла в виде спектра поверхностных электромагнитных волн

Большое число публикаций, посвященных изучению поверхностных электромагнитных волн (ПЭВ), обусловлено перспективами их эффективного применения в оптических системах и приборах. Оптическая обработка информации в наномасштабе является одним из основных направлений, где использование ПЭВ является особенно перспективным [1-3]. Решение задачи дифракции ПЭВ на микро- и нанобъектах, расположенных непосредственно на поверхности распространения, является ключевой задачей для применения ПЭВ в приложениях нанофотоники.

В работах [4-8] рассмотрены дифракционные структуры, предназначенные для преобразования и фокусировки ПЭВ. Результаты работ [4-8] указывают на существование явной аналогии между распространением и дифракцией ПЭВ и распространением и дифракцией света. В работе [9] рассматривается дифракция, возникающая при распространении ПЭВ по двум металлическим полосам в область сплошной металлической пленки (рис.1).

Рис.1. Схема эксперимента по дифракции ПЭВ на двух «щелях»

Указанный эксперимент является аналогом знаменитого эксперимента Юнга по изучению дифракции света на двух щелях. В [9] отмечено большое сходство между дифракционной картиной света на двух щелях и соответствующей интерференционной картиной ПЭВ. На основе наблюдаемого сходства авторами [9] записаны интегральные представления электромагнитного поля на поверхности распространения через угловой спектр ПЭВ. В [10] указанные представления использованы для расчета линзы ПЭВ и моделирования распространения ПЭВ.

Приведенные в [9,10] интегральные выражения по форме совпадают с представлением решения скалярной задачи дифракции через угловой спектр плоских волн [11, 12]. В работе [7] использован аналог интегрального представления Френеля-Кирхгофа для описания распространения ПЭВ.

В данной статье приведен строгий вывод интегрального представления электромагнитного поля на поверхности распространения через угловой спектр ПЭВ. Показано, что использованные в [7, 9, 10] соотношения являются приближенными. В статье получены уточненные аналоги интеграла Кирхгофа для моделирования дифракции и распространения ПЭВ.

Рассмотрим получение ПЭВ из решения уравнений Максвелла для двух полубесконечных сред с границей раздела при y = 0. При этом среды 1, 2 соответствуют областям y < 0 и y > 0 соответственно. В качестве оси распространения ПЭВ выберем ось Oz .

Получим предварительно общие выражения для компонент электромагнитного поля в средах 1, 2. Индекс номера среды в компоненты поля введем позднее, при наложении граничных условий на границе раздела сред. Поскольку свойства среды не зависят от x , то электрическое и магнитное поля в средах 1, 2 имеют вид

E ( x , y , z ) = E ( y , z )exp( ik 0 a x ), H ( x , y , z ) = H ( y , z ) exp( ik o a x ),

где k0 = 2п / X , X - длина волны. Подставляя (1) в уравнения Максвелла для монохроматического поля rot H = -ik08E, rot E = ik0H,

где s - диэлектрическая проницаемость, представим компоненты поля в средах 1, 2 через x -компоненты в виде

E y

E z

H y

H z

-1 ( 5 H 5 E ) —7 г I — + a — I, ik 0 ( e-a ² ) ( 5z 5 y J

1    ( 5H ri -aI ik0 (e-a2)( 5y5

1    ( 5E5

: 7-----ri e —--a —- |, ik0 (e-a2)( 5z      5y J

-1 ( 5 E 5 H ) : ,  1 e —- +a —- |. ik 0 ( e-a ² ) ( 5y 5 z J

Функции E_x , H_x в (3) удовлетворяют двумерным уравнениям Гельмгольца

5 ² E   5 2 E    _{г г}

,2 ⁺ _? 2 ^{+ k} o ^{( e-a} ) ^E - = 0,

5 y5

^H- +'⁵-H^L + k o(£-a ²) H_x = 0.

5 y5

Решения уравнений (4) для компонент H _x , E _x в средах 1, 2 имеют вид

HX' ( y , ^z ) = h ■ exp ( ^ik o P ^z ) exp ( ^k 0 Y 1 y ) , H^ ( y , ^z ) = h 2 ■ exp ( ^ik o P ^z ) exp ( ^{- k} 0 Y 2 y ) , E ™ ( y , ^z ) = e ■ exp ( ^ik o P ^z ) exp ( ^k 0 Y 1 y ) , Х ( y , ^z ) = e 2 ■ exp ( ^ik 0 P ^z ) exp ( ^{- k} 0 Y 2 y ) ,

где y 2 =- ^ s i -a ² ) + ₽ ², (6)

h i , e i , i = 1,2 - произвольные постоянные, а индекс i означает номер среды. Представления (5) соответствуют ПЭВ, поскольку имеют затухающий вид в направлении перпендикулярном границе.

Запишем условия равенства тангенциальных компонент электрического и магнитного поля на границе раздела сред при y = 0

H? ( 0, z ) = H - ¹ ( 0, z ) , E ( 0, z ) = Д) ( 0, z ) , E z ²’ ( 0, z ) = E^¹ ( 0, z ) , H^ ( 0, z ) = H z^ ( 0, z ) ,

где вид компонент E z‘ ) , H z‘ ) , i = 1,2 определен в (3).

Согласно (7), получим

h 1 = h ₂, e , = e ₂,

h ₁

Y 1           Y2      . „     ^-a i P       ^a i P

21 ⁺lo _„21 ⁺ e ¹      __г,2\ ⁺ /       2\

( e 1     ex   )    1 e 2     ex   )            ( e 1     ex   )    ( e 2     ex   )

h ₁

^-a i P        ^a i P              ^e 1 Y 1          ^e 2 Y 2

21      _„21 ⁺ e ¹     _„21      _„21

1 e 1     cx  ) 1 e 2     cx  )            1 e 1     cx   ) ( e 2     cx   )

Из (8) получим дисперсионное уравнение для определения константы распространения p

I Y 1 + Y 2 II ^e 1 Y 1 ₊ ^e 2 Y 2 l® 1 ® 2 Д ® 1 ® 2

-a ² p ² И - XI = 0, l® 1 ® 2 J

где

to i = e i - a = P - y i , i = 1,2.

Несложно показать, что решение (9) сводится к решению биквадратного уравнения относительно р ²

Р ² ( a ² ) = ( p 0 -a ² )

R 2^ ee e0

e 1 +£ 2

Уравнения (8) - (10) позволяют получить для функций H _x , E _x на границе раздела y = 0 интегральные представления, аналогичные представлению поля через угловой спектр плоских волн и интегралу Кирхгофа, которые широко используются в скалярной теории дифракции [11,12]. Действительно, запишем общее решение при y = 0 в виде суперпозиции ПЭВ

^H x ( x , ^z ) =

= j I ( a ) exp ( ik ₀ a x ) exp Ц ik ₀ P ( a ) z J d a ,

где функция в ( a ) имеет вид (9)-(10) или определяется из (10). Уравнение для E x ( x , z ) имеет точно такой же вид и в дальнейшем рассматриваться не будет. Уравнение (11) является аналогом представления поля через угловой спектр [11].Отметим, что выбранный базис не является полным и (11) является решением только в классе ПЭВ. При этом функция I ( a ) определяется через значения поля при z = 0 в виде

I ( a ) = 2^ j H-^ ( x , 0 ) exp ( - ik ₀ a x ) d x .      (12)

Подставляя (12) в (11), получим поле в виде

H x ( x , z ) = j I ( a ) exp ( ik ₀ a x ) x

X exp I iz^k Spp - k 02 a ² I d a ,

где k spp = k 0 P 0 - волновое число ПЭВ при а = 0.

Уравнение (13) полностью идентично интегральному представлению поля через угловой спектр плоских волн, используемому в скалярной теории дифракции [11. 12]. Уравнения (12), (13) позволяют записать аналог интеграла Кирхгофа для ПЭВ в виде

| x | <  R и равно нулю при | x | >  R . Разлагая H _x ( x , 0 ) в ряд Фурье, представим поле в виде

^H x ( ^x , ^z ) = exp ( ik spp z ) exp

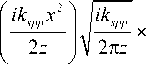
Hx (x, z) = j Hx (u, 0) G (x -u, z)du ,          (14)

где

G ( x , z ) = 2 j exp ( ik ₀a x ) exp ( ik ₀в ( а ) z ] d а (15)

Интегрируя, получаем, что ядро интегрального оператора (15) может быть представлено в виде

G (x, z) =

1 Г+”                /72       2

= — I exP (i (x П + Jkspp-П z))d n = 2nJ-”

x R ^ c n sinc n

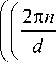
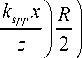
где c n - коэффициенты Фурье, sinc ( x ) = sin ( x ) / x .

Условие

ik z spp           1

2 _X x          ¹

[ k spp^ x ^{2 +} z ² ] ,

где n = k ₀а , , H 1 ( x ) - функция Ханкеля первого рода, первого порядка [14]. Заменяя функцию Хан-келя асимптотическим выражением при больших значениях аргумента [14], получим

G (x, z)

ik spp

\ 2 n g ² 7 x ² + z²

X

X , z    exp I ik_SDD ^x ² + z²

7x277 7 spp

Уравнения (14), (15) и (16), (17) являются прямыми аналогами интеграла Кирхгофа в двумерном случае. Разлагая корень в (17), получим ядро интегрального преобразования для аналога параксиального приближения Френеля

G (x, z)

I Ik spp

V 2n>jx ² + z²

X

^X / ,z , exp ( ik spp z ) exp V x + z

( ik x ² ) spp

2 z

.

Из (18) несложно получить аналог параксиального приближения Фраунгофера

H x ( ^x , ^z ) = exp ( ik spp z ) exp

( ik  x ² )

spp

2 z

X

d u .

Рассмотрим пример. Пусть входное поле

H_x ( x , 0 ) является периодическим с периодом d при

, . X n ■'k™ tg (an ) =   = -spp-,                         (21)

zd kspp = 2n / kspp определяет направления порядков дифракции.

Заключение

Полученные интегральные представления электромагнитного поля на границе раздела двух сред через угловой спектр ПЭВ объясняют использованные ранее представления и показывают их точный характер. Приведены аналоги интеграла Кирхгофа для описания дифракции поверхностных электромагнитных волн.

Работа выполнена при поддержке «Фонда содействия отечественной науке», фонда «Фундаментальные исследования и высшее образование» (RUXO-014-SA-06) и грантов РФФИ № 07-07-97601-р_офи, 07-01-96602-р_поволжье_а, 07-07-91580-АСП_а, 08-07-99005-р_офи, гранта Президента РФ № НШ-3086.2008.9.