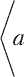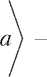Дистанционное зондирование Земли (ДЗЗ) автоматическими космическими аппаратами (КА) является активно развивающимся направлением. Получаемые таким образом изображения широко востребованы для ряда прикладных задач. Важной особенностью таких изображений является их привязка к географической системе координат, позволяющая установить, какой именно участок земной поверхности был снят. Одной из ключевых задач первичной обработки «сырой» информации, поступающей непосредственно с КА, является вычисление параметров этой привязки. Данные о геопривязке, как и сами изображения, необходимы конечным пользователям в виде, понимаемом геоинформационными системами — программами общего назначения, умеющими обрабатывать данные ДЗЗ.

Параметры геопривязки могут быть представлены в виде строгих (физических) и обобщённых моделей. Строгая модель наиболее точно описывает реальное движение КА по орбите во время съёмки, основываясь на данных о навигации, ориентации КА и на информации о его оптической системе. На этапе первичной обработки используется именно строгая модель, однако такую модель не всегда возможно интегрировать в геоинформаци-онные системы и передать конечному потребителю. Поэтому в индустрии нашли применение обобщённые модели, являющиеся унифицированными аппроксимациями строгих моделей.

Одной из основных обобщённых моделей геопривязки, широко используемой в индустрии, является модель рациональных функций ( rational function model — RFM ) [1]. Большинство современных геоинформационных систем умеют работать с этой моделью, что позволяет их пользователям рассматривать данные от различных аппаратов ДЗЗ в унифицированном «обезличенном» виде. Модель рациональных функций основывается на установлении соотношения между географическими координатами и координатами изображения (строка, столбец) в виде отношения полиномов третьей степени. Коэффициенты полиномов составляют параметры модели, для них принято обозначение RPC — rational polynomial coefficients .

Современные космические системы ДЗЗ характеризуются значительными объёмами целевой информации, формируемой космическими аппаратами. Это обусловлено развитием как оптических систем, позволяющих получать изображения земной поверхности в высоком пространственном разрешении (доли метра), так и радиотехнических средств, позволяющих полученные объёмы «сбросить» на наземные станции за непродолжительные, как правило, сеансы связи. Отсюда проистекает ряд требований к обработке целевых данных вообще и к алгоритму расчёта коэффициентов RPC в частности:

• •    автоматическая работа — алгоритм должен работать полностью без участия человека; в частности, это означает адаптируемость «на лету» к различным режимам съёмки;

• •    скорость — алгоритм должен работать как можно быстрее с целью минимизации времени получения изображения, готового для использования конечным пользователем;

• •    точность — алгоритм должен достигать хорошей точности аппроксимации, так как для многих прикладных задач важен каждый метр.

В настоящий момент в литературе описан ряд алгоритмов расчёта RPC , бóльшая часть которых основывается на решении линейной системы уравнений, полученной по конечному набору точек [2]. Хотя получаемые этими методами результаты хороши, развитие космической техники постоянно требует лучших алгоритмов. В настоящей работе предлагается альтернативный метод расчёта коэффициентов — интегральный.

В данной статье сначала вводятся необходимые обозначения и проводится общая математическая постановка задачи аппроксимации произвольной функции трёх аргументов рациональной функцией. Затем вкратце рассматривается дискретно-линейный метод и некоторые проблемы, возникающие при его применении. После этого излагается предлагаемый интегральный метод, который затем иллюстрируется на данных КА ДЗЗ EgyptSat-A .

Обозначения и постановка задачи

Через Rn будем обозначать евклидово пространство n-мерных вещественных векторов-столбцов с естественным скалярным произведением:

〈 a , b 〉 = a ₁ b ₁ + a ₂ b ₂ + … + a_nb_n .

Пусть x = [x1, x2, x3]T ∈ R3 (здесь и далее через верхний индекс «T» обозначается транспонирование). Мономом степени m от трёх переменных будем называть выражение xk1 xk2 xk3, где k1, k2, k3 — неотрицательные целые числа, причём k1 + k2 + k3 = m. Через h1(x), h2(x), …, h20(x) обозначим все мономы степени не выше третьей от трёх переменных, занумерованные в произвольном порядке. Введём вектор-функцию h(x) = [h1(x), h2(x), …, h20(x)]T, принимающую значения в R20. Обозначим p(x, a) = 〈h(x), a〉, где x ∈ R3 и a ∈ R20. Таким образом, p(x, a) — это полином третьей степени от x, порождённый вектором коэффициентов a.

Теперь можно рассмотреть общий вид задачи аппроксимации заданной функции рациональной функцией: по заданной гладкой функции f(x), определённой в области Ω ∈ R3, найти такие векторы a ∈ R20, b ∈ R20, что функция p (x, a )

P ( x, b )

в том или ином смысле приближает f ( x ) в области Ω.

Это задача параметрической аппроксимации, т. е. задача нахождения конечного набора коэффициентов, обеспечивающего наилучшее приближение заданной функции в известном семействе функций. Модель RPC однозначно задаёт семейство функций, в котором ищется приближение.

Для задачи геопривязки необходимо аппроксимировать две функции (отображающие географические координаты в строку и столбец соответственно), т. е. решить эту задачу дважды.

Дискретно-линейный метод

В задачах обработки данных ДЗЗ одним из самых распространённых методов построения аппроксимации рациональной функцией является свед алгебраических уравнений. Этот метод исходит из выбора конечного числа точек x1, x2, …, xm, значение f в которых известно, и рассмотрения отклонения аппроксимации в каждой из них. Поскольку так ошибка получается нелинейно зависящей от искомых параметров, то осуществляется переход к линейному отклонению p(xk, a) – f(xk)p(xk, b). После этого искомые коэффициенты определяются как решение следующей задачи:

E [ P ( X k , a ) — f ( X k ) P ( X k , b )]2 ^ min.

k = i a b

Эта задача представляет собой вариант хорошо известного метода наименьших квадратов. Для гарантии невырожденности матрицы коэффициентов, как правило, полагают коэффициент при константном мономе в знаменателе равным единице (тем самым также понижая размерность задачи). Проблемы такого подхода происходят из линеаризации ошибки, т. е. отбрасывания требования отсутствия у p ( x , b ) нулей в Ω [отличных от нулей p ( x , a )]. Полученные решения могут быть такими, что p ( x , b ) будет довольно близко к нулю. Это приводит к наличию видимых артефактов при применении этих коэффициентов для ортотрансформации изображения. Существуют различные методы для нивелирования этого эффекта, например применение метода роя частиц [3, 4] и регуляризация в норме l ₁ [5]. Эти методы, однако, оказываются на практике весьма вычислительно ёмкими.

Далее по тексту все интегралы берутся по Ω.

Для получения численного решения этой задачи можно использовать следующий итерационный алгоритм:

• 1)    выбрать некоторое начальное приближение b ₀ ;

• 2)    на k -м шаге, начиная с k = 1:

• а )    по ранее найденному b_{k –1} найти решение задачи

a_k = argmin J ( a , b_{k –1} );                     (1)

a

• b )    по ранее найденному a_k найти решение задачи

b_k = arg _b min J ( a_k , b );                       (2)

• с )    если не выполнен критерий останова, то перейти на следующую итерацию (шаг 2 , а ).

В качестве критерия останова можно брать обычные критерии, например достижение определённого значения невязки или исчерпание количества итераций.

Таким образом, итерация состоит из двух шагов: нахождения числителя по ранее найденному знаменателю и нахождения знаменателя по най-

Интегральный метод

Предлагаемый в настоящей статье интегральный метод исходит из рассмотрения приближаемой функции как элемента пространства L ²(Ω, R ) функций, интегрируемых по Лебегу вместе со своим квадратом [6]. Искомые параметры a , b предлагается искать как решение задачи минимизации отклонения рациональной функции от искомой по квадрату нормы пространства L ²(Ω, R ) (среднеквадратичного отклонения):

денному на первом шаге числителю.

Отметим ключевое отличие этого подхода от дискретно-линейного. В дискретнолинейном подходе дискретизация по аргументу проводилась до постановки задачи минимизации функционала ошибок; в интегральном же подходе дискретизация проводится после постановки задачи минимизации, и решение, как мы сейчас увидим, можно в определённом объёме проводить в непрерывном виде.

Рассмотрим каждый из шагов итерации отдельно.

Первый шаг. Корректность этого шага можно обосновать аналитически с помощью нижеследующей теоремы. Более того, для a_k можно предъявить явную формулу.

Теорема . Пусть вектор b и область Ω таковы, что всюду в области Ω p ( x , b ) ≠ 0 и функции h ₁ ( x ), h ₂ ( x ), …, h ₂₀ ( x ) линейно независимы в Ω. Тогда существует единственное решение задачи (1):

J ( a , b ) =

I

Q

P ( X, a a )

P ( X, b )

– f ( x )

a k

dx → min . a, b

I —:—,--- h~H ( x ) dx

p ( x, b_{k – 1} )²

\                           7

I

^{h ( x ) f ( x )} dx, p ( x, b_{k – 1} )

где H ( x ) = h ( x ) h ( x )^T.

Доказательство . Покажем, что минимизируемый функционал можно записать в следующем виде:

J ( a , b ) = 〈 a , M ( b ) a 〉 + 〈 a , c ( b ) 〉 + w .     (3)

Раскрыв скобки под интегралом, получим:

_u      f В ^{a ,} h ⁽ x ^ 9^ ^a ’ h ⁽ x^ f ⁽ x ) ₊

J ^{( a} ’ b ) = J          ^{- 2}--- ГТ— ⁺ f ⁽ x )² dx

p ( x, b )²           p ( x, b )

Рассмотрим квадрат скалярного произведения из числителя в первом слагаемом:

20               ₂       20

= 〈 a , h ( x ) h ( x )^T a 〉 = 〈 a , H ( x ) a 〉 .

Значит, функционал можно записать следующим образом:

J ( a , b ) =

f 1

J ~Т~шН( x ) dx

^ p ( x, b )²

- 2 [a , J ^h(xf) d\ + J f ( x )² dx.

\    p ( x, b )    /

Отсюда видно, что при фиксированном b функционал можно записать в виде выражения (3), где

M ⁽ b ) = J        H ⁽ x ) dx ;

p ( x, b)²

-2 J

c =

^h ( ^{x)f ( x} ) , dx ;

p ( X, b )

w = ∫ f ( x )² dx .

Заметим, что при этом матрица M(b) квадратичной формы является матрицей Грама функций h !( x)   h2( x)       h 2g( x)

,,…,   , p (x, b) p (x, b)     p (x, b)

линейная независимость которых следует из линейной независимости h_k ( x ) и того факта, что множитель p ( x , b )

нигде не обращается в ноль. Следовательно, эта матрица будет положительно определённой, и, значит, минимум функционала по a при фиксированном b J ( ⋅ , b ) будет достигаться на векторе

^– ₂ M ( b )^–1 c ( b ) [7], что при подстановке для нашего случая и даёт требуемый результат.

Второй шаг. Задача (2), к сожалению, не поддаётся непосредственному анализу, как задача (1). Для её решения придётся использовать численные методы (например, метод градиентного спуска [7]). Для их использования может оказаться полезной возможность указать градиент функционала по b в явном виде:

\ n P(x, a) л/ Op (x, a vb J(a, b ) = - 2 J - f(x) h (x) dx.

p ( x, b ) J p ( x, b )

Применение к задаче геопривязки

Как правило, параметры рациональной модели рассчитываются на этапе первичной обработки для каждого полученного изображения в съёмке. Рассмотрим вопрос применения описанного метода для изображения размером N × M пикселов; через I обозначим множество всех возможных позиций пиксела.

Как уже было отмечено, задача геопривязки моделью рациональных функций подразумевает нахождение параметров двух функций: преобразующей из географических координат в строку изображения, f_r , и преобразующей в столбец, f_c ; для краткости, обозначим ϕ( x ) = [ f_r ( x ), f_c ( x )]^T.

Функция ϕ( x ) неизвестна. Однако, поскольку расчёт параметров выполняется при известных данных положения и ориентации аппарата, известна обратная к ней функция ϕ^–1, которая переводит значения координат изображения в географические. Известна она, разумеется, приближённо и численно на основе телеметрических данных аппарата.

Таким образом, для применения метода нам необходимо:

• 1)    определить множество Ω;

• 2)    получить в Ω вспомогательную аппроксимацию ϕ( x );

  3) применить интегральный метод для нахождения аппроксимаций f_r , f_c — для этого придётся численно брать все необходимые интегралы.

  Граница трёхмерной области Ω естественно задаётся как отображение в географические координаты границы экстента изображения. Иными словами, пусть E = {ϕ^–1( p )} _{p ∈ д I} . Тогда положим

  
  

  Ω =

  
  

  min x ₁ , max x ₁ x g E    x g E

  
  

  ×

  
  

  min x ₂ , max x ₂ x g E    x g E

  
  

  ×

  
  

  min x ₃ , max x ₃ x g E    x g E

  
  

  Таким образом, Ω является параллелепипедом. Непосредственно проверяется линейная независимость мономов в Ω, необходимая для корректности первого шага итерации.

  Можно предложить два подхода для аппроксимации функции ϕ( x ), непосредственно влияющих на дальнейшее численное интегрирование.

  Первый подход заключается в выборе на изображении некоторой сетки с множеством индексов U ⊆ I , тогда можно получить сетку в географических координатах

  
  

  X = {ϕ^–1( p )} p ∈ U .

  
  

  Таким образом, можно считать ϕ известной на X и далее двигаться через интерполяцию. Основной трудностью при таком подходе является нерегулярность полученной сетки X , на ней будет затруднительно проводить численное интегрирование.

  Второй подход состоит в разбиении Ω вдоль одной из географических координат с последующей аппроксимацией среза ϕ( x ) на каждом из получившихся «слоёв». На роль координаты разбиения (из числа географических координат) естественно подходит высота. На каждом из слоёв мы получаем функцию двух аргументов, для численной аппроксимации которых есть зарекомендовавшие себя на практике методы, например тонкостенные сплайны [8].

  Главным преимуществом второго подхода является возможность посчитать функцию на регулярной сетке, т. е. возможность применить простые методы интегрирования. Более того, для обеих задач (для f_r и для f_c ) функции h ( x ) и H ( x ) будут одинаковыми, т. е. можно заранее посчитать их на одной сетке.

  
  

  Результаты применения

  Предлагаемый метод был применён в системе первичной обработки данных КА ДЗЗ EgyptSat-A , разработанного РКК «Энергия».

  В системе обработки в качестве географических координат используются геодезические координаты (долгота, широта, высота) земного эллипсоида WGS84 . При работе со снимками протяжённостью порядка 10–15 км такую систему координат допустимо считать прямоугольной.

  Для аппроксимации целевой функции был выбран второй подход, основывающийся на использовании дополнительных численных приближений тонкостенными сплайнами на четырёх высотных слоях. Для решения задачи (2) использовался метод градиентного спуска.

  В качестве критерия останова алгоритма было выбрано достижение порогового изменения значения функционала [т. е. останов наступал, как только разница J ( a_{k +1} , b_{k +1} ) – J ( a_k , b_k ) становилась меньше заданной]. Алгоритм достигает останова в среднем за две-три итерации, для вычисления знаменателя (шаг 2, b ) требуется порядка трёх-четырёх итераций метода градиентного спуска. Оценка алгоритма осуществлялась по ошибкам точности привязки относительно строгой модели (невязке). В качестве эталонного был взят другой алгоритм, основанный на методе роя частиц. Всего было обработано около 200 реальных снимков с различными условиями съёмки. Снимки были разбиты на четыре группы, исходя из условий съёмки.

  Сравниваемые алгоритмы показали сопоставимую точность привязки относительно строгой модели. Разница ошибок привязки между двумя алгоритмами в среднем не превышает 1 пиксел по изображению (значения представлены в таблице), за счёт чего при использовании в дальнейшей обработке (например, ортотрансформировании) оба метода дают результаты, отличающиеся субпиксельно.

  Как отмечалось ранее, алгоритмы нахождения коэффициентов могут давать решения, применение которых приводит к заметным артефактам, обусловленным близостью к нулю знаменателя рациональной функции. Оба рассматриваемых метода демонстрируют отсутствие подобных эффектов.

  
  

Сравнение невязок алгоритмов относительно строгой модели в пикселах фокальной плоскости

Набор данных	Интегральный метод	Дискретно-линейный метод
Отклонение от надира менее 10 ° , перепад рельефа менее 300 м	1,000	0,8767
Отклонение от надира менее 10 ° , перепад рельефа более 500 м	1,560	0,9834
Отклонение от надира более 15 ° , перепад рельефа менее 300 м	1,739	0,9255
Отклонение от надира более 15 ° , перепад рельефа более 500 м	1,192	0,8206

Предлагаемый алгоритм значительно превосходит эталонный по времени расчёта. На сценах из всех четырёх наборов данных среднее время вычисления коэффициентов модели эталонным алгоритмом составляло 3 мин, а для интегрального алгоритма — 2,5 с. Это можно объяснить тем, что метод роя частиц для достижения требуемой точности использует значительное количество частиц, начальное распределение которых не зависит от условий задачи, многие частицы оказываются далекими от оптимума, однако вычисления для них продолжаются. Предлагаемый алгоритм осуществляет поиск из одной стартовой позиции.

Заключение

Предлагаемый в статье интегральный метод расчёта коэффициентов модели рациональных функций показал себя пригодным для использования в первичной обработке реальных данных от КА ДЗЗ EgyptSat-A . Продемонстрированные им показатели точности и скорости расчёта позволяют сделать вывод о возможности применения метода в высоконагруженных системах обработки информации ДЗЗ. Заложенная в общей формулировке метода алгоритмическая гибкость позволяет адаптировать его к особенностям различных КА ДЗЗ.

В качестве дальнейшей работы представляет интерес изучение границ точности предложенного итерационного алгоритма, а также изучение влияния траекторных свойств съёмки на точность аппроксимации. Отдельным интересным моментом для дальнейшей работы является изучение численной устойчивости алгоритма для выяснения границ его применимости.