Интегрирование бигармонического уравнения по неявной схеме

Краевые задачи для бигармонического уравнения возникают в теории упругости при моделировании изгибов тонких пластин [1–2], а также в гидродинамике при моделировании свободно-конвективных течений [3–5].

Наиболее известное решение неоднородного бигармонического уравнения, так называемого уравнения Софи Жермен, получены Анри Навье в виде двойного тригонометрического ряда. Однако оно справедливо лишь для пластинок, шарнирно опертых по контуру. Ряды в этом решении сходятся медленно. Более общее решение предложил Морис Леви, но и им не исчерпываются все постановки граничных условий.

В связи с отсутствием аналитических решений широкое развитие получили численные методы интегрирования краевых задач для бигар-монического уравнения. Наряду с классическими [6–7] используются и современные методы, такие как метод конечного множества точек [8–9].

Построение конечно-разностной схемы

Рассмотрим краевую задачу для неоднородного бигармонического уравнения с граничными условиям и первого и второго рода в квадратной области D = [0;1] х [0;1] .

д⁴Ф ( X , Y )   ₂ д⁴Ф ( X , Y )   д⁴Ф ( X , Y )

дX4       дX 2д Y2

Ф(0, Y ) = Ф(1, Y ) = Ф( X, 0) = Ф( X, 1) = 0,

• дФ(0, Y) = дФ(1, Y) = дФ( X ,0) = дФ( X ,1) = Q (3 ) ∂X      ∂X      ∂Y∂

Выбор разбиения осуществлен таким образом, чтобы в него попадали точки границы области и центр области.

Для построения конечно-разностного аналога частных производных д ⁴ Ф ( X , Y )/ д X ⁴ и д ⁴ Ф ( X , Y )/ д Y ⁴ используем центрально-разностный оператор 2-го порядка примененный дважды по соответствующей переменной:

Конечно-разностный аналог смешанной производной д 4Ф дX 2д Yг

144(A X )²(A Y )² Й^{Ф 1 + 2,} j ^{+ 2  16 Ф} - ^{+ + +}

^{30 Ф} i + 2, j  1^{6 Ф} 2    ^+Ф i + 2, j — 2 ) ^{- 16} ( ^Ф„   1^{6 Ф} i + 1, j + 1 ⁺

+30Ф i + 1, , - 16Ф i + 1, _/ - 1 +Ф i + 1, j — 2 ) + 30 ( Ф i , j + 2 — 16Ф, _{у +} 1 +    ⁽⁶⁾

+30Ф  - 16Ф  . + Ф ,)-16(ф .   -16Ф ,  , + i,j              i,j-1         i,j-2 )          \ i-1,,+2             i-1,,-2

д4Ф . Фi+2,j - 4Фi+1,, + 6Фi, - 4Фi-1,j +Фi-2,j(4)

дX4 i,,( д4Ф  _ Фi,j+2 - 4Фi,, + 1 + 6Фi,, - 4Фi,,-1 +Фi,-2

д Y⁴ i,j                      ( A Y ) ⁴

+30Ф^ 1, , - 16Ф i - 1, , - 1 +Ф i -_{k /} - 2 ) + ( Ф i - 2, j + 2 - 16Ф i - 2„ , + 1 +

+30Ф ‘ - 2„ , -16Ф k - 2, j - 1 +Ф k - 2, j - 2 ) ]

Подставив в уравнение (1) аппроксимации производных (4)–(6), получим разностное уравнение

^Ф . + 2,j ^{- 4 Ф} i + 1, , ^{+ 6 Ф}у" ^{4 Ф} i - 1, , ^+Ф i - 2,j , ^Ф i,j + 2 ^{- 4 Ф} y+ 1 ^{+ 6 Ф}у^{- 4 Ф}y- 1 ^+Фy- 2

( A X )⁴                                   ( A Y )⁴

+ 72(AX) 2(^)2 [ ( Ф' + 2, , + 2 - ^{16 Ф} ' + 2, У + 1 + ^{30 Ф} • + 2, j - 1⁶ Ф- + 2, , - 1 + ^Ф , +_У- 2 H⁶( ^Ф _г +у+ 2 - ^{16 Ф} . + 1,j + 1 + ^{30 Ф} i + 1, j - ^{16 Ф} _г +у- 1 + ^Ф _г +у- 2 ) +    ⁽⁷⁾

+ 30 ( Ф, , + 2 - 16 Ф, , .+ 1 + 30 Ф i , j - 16 Ф, j - 1 +Ф, j - 2 ) - 16 ( ф„ - 16 Ф _; - 1, j - 2 + 30 Ф k - 1j - 16 Ф k - 1, j - 1 +Ф k - 1, j - 2 ) +

+ ( Ф k - 2,j + 2 - 16 Ф k.y + 1 + 30 Ф ^

Граничные условия (2) накладываемые на искомую функцию приобретут вид

^Ф 0, j = ^Ф n,j = ^ф ,0 = ^ф п = ⁰, i = ⁰, n^,j = ⁰, n (8)

Граничные условия накладываемые на частные производные первого порядка получим, используя разностные операторы для левой и правой границ дФ _ -3Ф, ,0 + 4Ф,,1 -Ф, ,2

дX i ,0

ЭФ ЗФ -4Ф , +Ф , i,n            i,n-1

дX i,n2

i = 1,..., n - 1   (9)

i = 1,..., n -1    (10)

Для верхней и нижней границ будем

• ^{- 16 Ф} k - 2, j - 1 ^+Ф k - 2, j - 2 ) ] = ^{- 1}

Тогда уравнение (7) примет вид

Вь Ф = - 1 h

Чтобы определить погрешность аппроксимации образуем разность z = u - v , где u -решение задачи (7), (8), (13), (14), а v – решение задачи (1)-(3). Подставляя u = z + v в уравнение, получим для z задачу

Bu = В (z + v) = Bz + Bv = -1, Bz = -£B во внутренних узлах сетки и для z выполнены граничные условия (8), (13), (14), где ^ = B^v + 1 -погрешность аппроксимации задачи (1)–(3) схемой (7), (8), (13), (14). Так как A2v+1 = 0, то иметь соответственно дФ _ -3Ф0,2+ 4Ф1„, -Ф2, дY 0,j          2AX        ’ дФ _ 3Ф„,j - 4Ф „1В +Ф„2,j. дY „,j          2AX j = 1,...,n -1 (11)

j = 1,..., n - 1 (12)

Заменим в уравнении (3) производные их конечно-разностными аналогами (9) – (12). Тогда, учитывая уравнение (8), граничные условия на производные примут вид

Фи = 1 ф .2 , ф i.„ - 1 = 1 ф i.„ - 2 , i = 1,..., n - 1 ⁽¹³⁾

• ^Ф 1,, = ^ ^Ф 2, j ^{, Ф} n - 1, j = ^{1 Ф} n - 2, j ^, j = l^,...^, n - ^{1   (14)}

В итоге непрерывная краевая задача (1) – (3) свелась к конечно-разностной схеме (7), (8), (13), (14).

Вычисление погрешности аппроксимации

На равномерной сетке A X = A Y = h обозначим

• = Bv + 1 - A ² v - 1 = Bv - A ² v . B

Вычислим погрешность аппроксимации почленно, используя разложение по формуле Тейлора с остаточным членом в форме Лагранжа, в окрестности i , j -того узла:

д ⁴ v     д ⁴ v ( X , Y )

д X⁴ i , j     д X⁴

h ² д⁶ v _r,z.

= T X^{[h (} i ^{+ n} ) jh ^],

0 <  n < 1,

д4 v    д4 v (X, Y)_ д Y4 i, j      д Y4

= hr Xv [ ih , h ( j + ° ")],  0< CT <1,

6 ду д4 v       д4 v (X, Y) = дX2дY2 i,j   дX2дY2 ”

B

h

д ⁴ Ф „  д ⁴ Ф     д ⁴ Ф

---Т + 2---7---- +---- дX4 i,j    дX2д Y2 i,j  д Y4

17 h ⁴ J d ⁸ V                d ⁸ v

"756" 1 aF ^{[( i + n h ,} hj ^{] +} aF ^{[ ih , h (} j ^{+ 7 )]}

—

34 h⁴

^J  d ⁸ v

1 — i — [ ( i + n ) h , h ( j + 7 ) ] + [a X ⁷ d Y

+ —7— [(i + n) h, h (j + 7) ]f — d Y7 dX

167 h ⁴ J d ⁸ v

--1 — г —7 [ ( ¹ + n ) h , h ( j + 7 ) ] +

270 lax6ayг d V1

+1 (i + n) h, h (j + 7) If — d Y6 dX2

34h4 Ja

--1 —;—г I ( i + n ) h , h ( j + 7 ), к т I +

5^V3

a ⁸ v

+ ~—T~—: d Y ⁵ d X

[ ( i + n ) h , h ( j + ст ), k T ] f +

85 h⁴    d ⁸ v

54 d X ⁴d Y⁴

[ ( i ⁺ n ) h , h ⁽ j + 7 ) ] ,0 <  n <  1,0 <  7 <  1.

Обозначим

M_x = max

• ¹     ( X , Y ) g D

d ⁶ v ( X , Y ) dX⁶

M, = max

• ²     ( X , Y )e d

a ⁶ v ( x , y ) d Y⁶

M, = min_

• ³     ( X ,Y )e D

d m ⁺ n v ( X , Y ) d X^m d Y n

, m , n = 1,3,5,7, m + n = 8;

M 4

= max_

( X , Y )e D

d ^{m +} n v ( X , Y ) d X^m d Yⁿ

, m , n = 2,4,6,8, m + n = 8.

Поскольку бигармонический оператор симметричен M^ = M ₂. Обозначим M_x = M_x /3 , M₂ = (5398/945) M ₄ — (1088/189) M ₃, тогда

| ^ | < M_xh ² + M₂h ⁴. (15)

Таким образом, разностный оператор аппроксимирует бигармонический со 2 порядком.

Граничное условие (2) на искомую функцию с учетом (8) аппроксимируется точно. Погрешность аппроксимации граничного условия (3) уравнениями (13) и (14) оценим используя разложение по формуле Тейлора с остаточным членом в форме Лагранжа, в окрестности i , j -того узла:

av  —av aXi,j  ax

2,2 d ³ V

= 3 h aF^[ h ⁽ i ⁺ n ), jh ]’

0 <  n < 1 .

Обозначим

M = max_

( X , Y ) e D

d³ v ( X , Y ) d X³

тогда | ^ | < Mh ² .

Итак, граничное условие (2) аппроксимируется также со вторым порядком, поэтому конечно-разностная схема (7), (8), (13), (14) аппроксимирует краевую задачу (1)–(3) со вторым порядком точности.

Анализ решений

Решение задачи (7), (8), (13), (14) вычислено с помощью системы компьютерной алгебры Maple для равномерной сетки с шагом h = 1/120. На рисунке 1 показан график решения, а на рисунке 2 его профиль в сечениях плоскостями X = 0.5 и Y = 0.5 . На рисунке 3 показаны профили решения в сечениях плоскостью Y = X и Y =1 — X. По графикам видно, что решение симметрично относительно центральной точки (0.5; 0.5), в кото рой достигается минимум равный —1.22 • 10—3.

В таблице 1 показана зависимость минимума функции от числа значимых цифр в расчете, т.е. фактически от погрешности округления. Расчет выполнен для сетки размерностью 81 х 81 точек. В столбце относительная разница минимумов функции показано насколько процентов результат отличается от предыдущего.

Здесь же приведено время расчета и егоот-носительное изменение. По таблице видно, что при увеличении числа значащих цифр с 14 до 16 время расчета увеличивается на 166% а точность всего на 3 * 10 ^{— 6} %. Эти данные говорят о том, что дальнейшее уменьшение погрешности округления приведет к значительному увеличению времени расчета при неизменном результате. Таким образом, 14 значащих цифр - оптимальным значение.

В таблице 2 отражена зависимость минимального значения функции от величины шага сетки и относительная разница минимумов функции. Здесь же приведено время расчета и его относительное изменение.Расчет выполнен с 14 значащими цифрами. Уменьшение относительной разницы минимумов функции по экспоненциальному закону свидетельствует о быстрой сходимости конечно-разностной схемы.

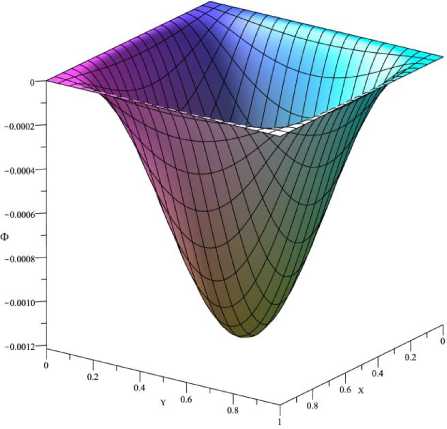
Рисунок 1. График решения

Figure 1. Solution graph

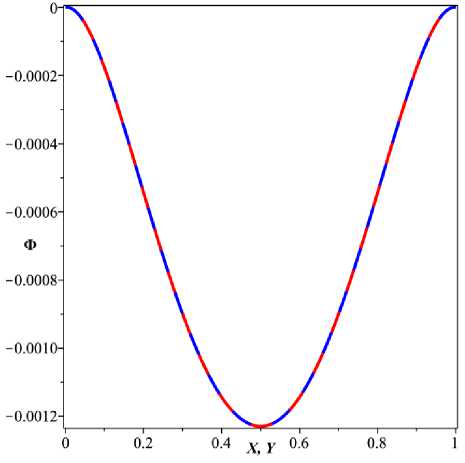
Рисунок 2. Профиль решения в сечении X — 0.5

Figure 2. Solution profile in section X — 0.5

Уменьшение относительного приращения времени расчета позволяет сделать расчеты более точными. Однако уменьшение шага сетки потребует увеличения значащих цифр, поэтому значение шага 1/120 является оптимальным

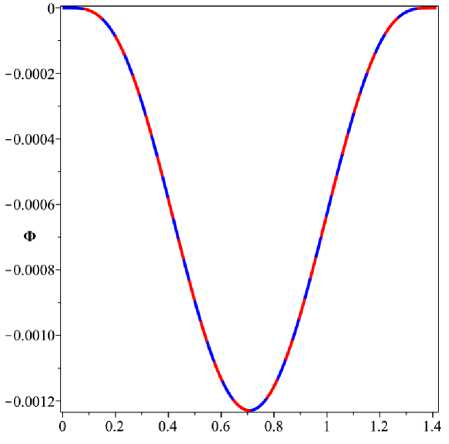
Рисунок 3. Профили решения в сечениях y — х (красный) и y — 1 — х (синий)

Figure 3. Solution profile in section y — х (red) and y — 1 — х (blue)

Полученный результат согласуется с численным решением данной задачи по явной схеме [10] и приближенно-аналитическим решением [11]. Значение функции в центральной точке для которых равны — 1.05 - 10 - ³ и — 1.25 - 10 ^{— 3} соответственно.

Таблица 1.

Погрешность округления

Table 1.

Rounding error

Число значащих цифр Number of significant digits	Минимум функции The minimum of a function	Относительная разница минимумов функции, % The minimum of the relative difference in the minimum of a function, %	Время расчета Calculation time	Относительная разница времени расчета, % Relative time difference calculation, %
8	-0.0012409828		333.687
10	-0.001202252713	-3.12	324.56	-2.74
12	-0.00120187713348	-0.03	326.96	0.74
14	-0.0012018733801815	-0.0003	332.969	1.84
16	-0.001201873342732467	-3 - 10 - 6	888.996	166.99

Таблица 2.

Скорость сходимости

Table 2.

Rate of convergence

Шаг сетки Grid spacing	Минимум функции The minimum of a function	Относительная разница минимумов функции, % The minimum of the relative difference in the minimum of a function, %	Время расчета Calculation time	Относительная разница времени расчета, % Relative time difference calculation, %
1/20	-0.0010105920924147		1.357
1/40	-0.0011381686297206	12.62393987	14.165	943.8467208
1/60	-0.0011806597334856	3.733287131	86.44	510.2364984
1/80	-0.0012018733801815	1.796762133	332.969	285.2024527
1/100	-0.0012145881472324	1.057912357	1090.431	227.4872436
1/120	-0.0012230583683455	0.6973739223	3259.407	198.9099723

Заключение

С помощью неявной конечно-разностной схемы получено решение неоднородного бигармонического уравнения. Путем разложения функции в ряд Тейлора вычислена погрешность аппроксимации бигармонического оператора разностным аналогом и погрешность аппроксимации граничных условий. Проведен анализ скорости сходимости схемы. Преимущества использования данной неявной схемы по сравнению с явной заключаются в ее абсолютной