Интегрирование по Риману многозначных отображений

Проблему интегрирования многозначных отображений F : T ^ 2 E исследовали многие ученые, начиная со второй половины двадцатого века. В случае, когда пространство E является конечномерным евклидовым пространством R ”, основное признание получило понятие интеграла. Аумана. (R.J. Aumann) [1] как совокупности значений от всех интегрируемых по Лебегу ветвей многозначного отображения. Такой подход был обоснован рядом хороших свойств этого интеграла, в первую очередь тем, что его значение является выпуклым и компактным множеством в R ”. Имеется целый ряд работ, развивающих и обобщающих результаты Аумана, (см., например, [2-6]), в том числе для случая, когда пространство E является банаховым (см., например, [7,8]).

В данной работе автор развивает свои результаты [9-12], основанные па. другом подходе к определению интеграла, от многозначного отображения с компактными значениями, опирающийся на. частичную линейность совокупности подмножеств из банахова, пространства, получаемую использованием понятия суммы множеств по Минковскому. Такой подход позволяет развивать классическое понятие интеграла. Римана, па. случай многозначного отображения. В работе обобщаются результаты, полученные автором ранее для случая многозначных отображений с компактными значениями из R ”, на случай отображений с компактными значениями из равномерно гладких банаховых пространств. Показано, в частности, что в таких банаховых пространствах интеграл Римана, па. отрезке, определяемый как предел римановых сумм от ограниченного невыпуклозначного отображения, является выпуклым компактом. До-

"Работа выполнена при поддержке РФФИ, инновационной России».

казаны необходимые и достаточные условия интегрируемости невыпуклозначного миогозиачиого отображения со значениями в сепарабельном равномерно гладком банаховом пространстве.

• II.    Определения и вспомогательные результаты

Через 2 E обозначаем множество всех подмножеств из банахова пространства E, через K ( E ) — множество всех непустых компактов из банахова пространства E, через co K ( E ) — совокупность всех выпуклых подмножеств из K ( E ). Если задан компакт X е K ( E ), то ^герез K ( X ) обозначаем совокупность всех непустых компактов из E, которые содержатся в X.

Алгебраической суммой (иначе называемой суммой Минковского) непустых множеств A и B из банахова пространства E называется множество A + B = {x| x е E. x = a + b. a е A. b е B}. Произведением множества A C E, A = 0, на число X е R¹ называется множество XA = {x е El x = = Xa. a е A}. Полунормой множества A е E называется число ||A[ = sup {||a||| a е A}.

В пространстве K ( E ) можно определить расстояние между двумя компактами A, B е K ( E ), которое задается метрикой Хаусдорфа:

h ( A,B ) = inf {г > 0 | A C B + Br (0) ,

B C A + Br (0) }, (2 . 1)

где Br ( a ) = {x е E | |x — a| < г} — открытый шар радиуса, г >  0 с пентрозi в точке a е E.

Пусть в банаховом пространстве E задано замкнутое множество A. Пусть E* — пространство, сопряженное к пространству E.

грант 10-01-00139а и ФЦП «Научные и научно-педагогические кадры

Опорной функцией множества A называется скалярная функция s ( p,A ) аргумента p е E*, определяемая равенством

1) Тогда множество D = liminf Dk, если оно не k→∞ пусто, будет выпуклым замкнутым множеством из E.

s ( p, A ) = sup {hp, xi | x е A},       (2.2)

где hp, xi — значение линейного функционала. p в точке x.

Пусть {Ak}p=1 — последовательность замкнутых множеств из банахова пространства E, содержащихся в некотором ограниченном подмножестве пространства E. Совокупность всех точек x е E, для каждой из которых найдется последовательность {xk}p=1. xk е Ak. така.я. что x = = lim xk, называется нижним пределом последо-k→∞ вателъности {Ak}k=1 и обозначается liminf Ak.

k→∞

Модулем гладкости банахова пространства E называется функция %: [0 , + го ) ^ [0 , + го ) вида

% ^{( Т} ) = |

^x + У

x-y

— 1 | x,y е E,

HxH = ¹ , kyk = ^т|.

(2 . 3)

В силу определения модуль гладкости % ( • ) является выпуклой возрастающей функцией, причем % ( т ) 6 т при всех т >  0.

Банахово пространство E называется равномерно гладким, если его модуль гладкости является о -малым от т при т ^ +0. т. е. lim % ^{( т )} = 0. т ^ +о ^т

Примерами равномерно гладких банаховых пространств являются гильбертовы пространства, пространства Лебега L_p [ a, b ] при p >  1 и другие (о равномерно гладких пространствах см, например, [13]).

В силу монотонности модуля гладкости пространства E для функции % ( • ) из (2.3) существует ее обратная функция %^- 1( • ), причем в случае, когда пространство E является равномерно гладким, очевидно, справедливы выражения

2) Если последовательность {Dk} сходится в метрике Хаусдорфа, то и последовательность {Dk} также сходится, причем к тому же пределу. □ Доказательство. Из условия следуют включения Dk С X V k е N 11 D С X. а также то. что рассматриваемые множества Ap, как подмножества X, ограничены в совокупности по полунорме, т. е. существует число а <  + го такое, что ||Ap| | 6 а при любых k,p.

1. Множества Dp и непустое (по условию) множество D = liminf Dk очевидно являются замкну-k→∞ тыми множествами. Покажем выпуклость множества D, т. е. покажем, что для всякой пары точек x. у из D и всякого числа. А е [0, 1] точка. z = Ax + (1 —A)у также принадлежит множеству D. По определению нижнего предела, для выбранных точек x, у е D существуют последовательности точек {xp}p=1. {yp}£LV xp е Dp. yp е Dp такие, что x = lim xp и у = lim yp. В свою очередь, для k→∞        k→∞ каждого числа k е N найдутся точки xp, е Ap., yp е Ap пРи p е (1, k) такие, что справедливы равенства xp = k (xp + + xp), yp = k (y1 + + yp).

Построим последовательность точек {z_k}k =₁, zp е Dp вида zp = ¹ ( zp + + zp ), где точки zp е е Ap в паре со вспомогательными точками Sp е E

будем вычислять по формулам: Sk ¹ = 0 ,

p zp =

J xp , если Sp

I yp , если Sp

- 1

- 1

+ y_k^p

+ y_k^p

-x

-x

p

'k

p

'k

>

sp = sp- ¹ + ( Axp + (1 — A ) yp —

сp^{- 1} , _тp _ ,,p

Sp + xp  yp p-1    p p°

Sp + xp   yp ■ zp)  V p е (1, k).

lim _^т = 0 , т ^ +о % 1( т )

lim т ^ +0

%- 1( т ) = 0 .

(2.4)

При этом при выборе zp = xp получаем равенство Sp = Sp ¹ + (1 — A )( yp — xp ). из которого очевидно следует оценка.

ISpk 6 max {|Sp^{- 1} k, |Sp^{- 1} + yp — xp||},

Для обоснования основных результатов нам потребуется следующая теорема, об усреднении множеств, являющаяся обобщением аналогичной теоремы из [11], полученной для гильбертовых пространств. Данное обобщение получено мною совместно с Г.М. Ивановым и представлено к печати в И-

Теорема 2Л (об усреднении). Пусть в равномерно гладком банаховом пространстве E

а при выборе zp = yp получаем равенство Sp = = Sp ¹ + A ( xp — yp ), из которого следует оценка

ISpk 6 max {|Sp^{- 1} k, kSp^{- 1} + xp — yp|}.

В итоге получаем общую оценку kSpk 6 max{kSp-1 k, min{kSp-1 + yp — xpk, kSp-1 + xp — ypk}}. (2.5)

задано выпуклое ограниченное замкнутое множество X. Пусть Ap, г де k е N, p е (1, k), — двухпараметрическое счётное семейство (невыпуклых) замкнутых подмножеств множества X. Опреде-kk лим множества Dk = 1 52 Ap и Dk = 1 52 coAp p=1               p=1

при k е N.

По определению модуля гладкости % ( • ) (см. (2.3)) в случае, когда Sp 1 =0, справедливо неравенство

Sp- ¹ + yp — xp kSp^{- 1} k kSp^{- 1} k

+

Sp- ¹ + xp — yp kSp^{- 1} k i s - ¹ k

6 2(1+ % (^y H ¹ ))• kS k

откуда (и учитывая, что Цур) — Xk k 6 2 а ) получаем

min-^

ST1 + yk — Xk kSkp-1k    kSkp-1k

Sk kSkp-1k

+

x

p

k

p yk

_{kS k}p- 1 _k

6 1 + %    —    . (2 . 6)

_{kS k}p- 1 _k

В итоге из выражений (2.5) и (2.6) получаем, что для любых p 6 (2 , к ), при которых S^ 1 = 0, справедливы неравенства.

^{ks a6 ks r 1 i} (¹⁺ %(s- ii)) .    ^,2-⁷'

Кроме того, для любого p 6 (2 , к ):

iSi 6 iSp^{- 1} i +2 а.           (2.8)

Определим числовую последовательность a^ = — 2^{1 4} npii всех к 6 N. г,те %- ¹ ( • ) — об-

% ч к )

ратная функция к модулю гладкости. В силу (2.4) получаем, что lim ak = + го,    lim Д = 0.     (2.9)

→ + ∞          → + ∞ k

Поэтому найдется номер к 0 такой, что a_k >  2 а при всех к >  к о, т. е., в частности, получаем оценку

iS ^ i 6 2 а < ak V к >  к о .       (2.10)

Для всякого к >  к о докажем оценку HS^ i 6 6 2 ea_k. Ес ли iS i 6 a_k, то требуемое неравенство очевидно верно. Пусть iS i > a_k. Тогда согласно (2.10) существует номер m > 1, m < к, такой, что справедливы неравенства iS^i > ak при всех p = к- к — 1..... m + 1. и о iSri 6 a_k. Поэтому в силу неравенств (2.6), (2.7) и определения

ak получаем

S" 6 ^iSk- ^{1 i} (^{1 +} % (^ ) )⁶

^{6 iSk- 1 i} (¹⁺ % (2 a )) = ₂

= iSk^{- 1} i (1 + 1 ) 6 iSk^{- 2} i (1 +1) 2 6 ...

k-m- 1

6 iSr ⁺¹ i     -}      6

k-m- 1            k-m- 1

^{6 ( iSri + 2 а} ) (^{1 +} д < ² ak (^{1 +} к) < ² ake.

сюда и из очевидного неравенства h(Dk ,D) = = h(CoDk, CoD) 6 h(Dk,D) получаем. что D = = lim Dk. Теорема доказана.                ■ k→+∞

Пусть T,Y — произвольные множества. Многозначным отображением F множества T во множество Y называется такое соответствие, когда каждой точке t 6 T сопоставляется некоторое (возможно пустое) подмножество F ( t ) С Y, называемое значением отображения F в точке t. Такое многозначное отображение будем записывать в вило F: T ^ 2 Y.

Если значения многозначного отображения F, т. е. множества F ( t ) при всех t 6 T замкнуты, компактны или выпуклы и компактны в E, то будем записывать соответственно в виде F: T ^ F ( E ), F: T ^ K ( E ) 1i F: T ^ co K ( E ).

Отображение F: T ^ K ( E ) называется компактно ограниченным, если существует выпуклый компакт X С E такой, что F ( t ) 6 K ( X ) V t 6 T.

Отображение F: T ^ K ( E ) называется непрерывным в точке t ₀ 6 T е метрике Хаусдорфа, если для любого числа е >  0 существует окрестность U ( t о) то^inn t о такая, чтс) для всех t 6 U ( t о) справедливо неравенство h ( F ( t ) , F ( t _о)) < е.

Теорема 2.2. Пусть T — топологическое пространство, X — выпуклый компакт из равномерно гладкого банахова пространства E, и число Y < + го. Тогда, для лтобого числа, е > 0 найдется число v = v(е,Х) > 0 такое, что для любого конечного набора точек {^i}ie/ С T, для любого конечного набора положительных чисел {А^}^е/, таких. что ^2 Ai = 1 и max {Ai | i 6 I} < v. а также i∈I для любых многозначных отображений G : T ^ ^ co K (X) и F: T ^ K (X). удовлетворятотттих оценке

h ( G ( t ) , co F ( t )) Vt 6 T, (2.11)

справедливо неравенство

h (X G ( ^i ) Ai, X F ( ^i ) Ai) + e. □ (2 . 12) i ∈ I              i ∈ I

Согласно полученной оценке для любого к > к0 имеем iAxk + (1 — A)yk — zki = 1 iSki < 2e^ ,

откуда, и из (2.9) следует, что построенная последовательность {z_k}k =₁, z_k 6 D_k, сходится к точке z = Ах + (1 — А ) у- то есть z 6 D. Выпуклость множества. D доказана.

2. По построению получаем равенство D_k = = co D_k. По доказанному выше множество D = = lim Dk является выпуклым множеством. От- k→ + ∞

Доказательство. Из условия теоремы следует, что для любого конечного набора, положительных чисел {Ai}ie/, таких, что 52 Ai = 1, и лю-i∈I бого конечного набора точек {ф}щ/ С T и любой пары многозначных отображений G, F, удовлетворяющих условиям теоремы (неравенству (2.11)), справедливы включения

X F ( ^i ) Ai С X G ( ^i ) Ai + B y (0); i ∈ I               i ∈ I

X G ( ^i ) Ai С X co F ( ^i ) Ai + B y (0) . i ∈ I               i ∈ I

Допустим, что неравенство (2.12) не верно. Тогда, учитывая первое включение в (2.13), получаем, что найдутся: 1) число е _о >  0, а также для каждого к 6 N, 2) пара многозначных отображений

(2.13)

Gk, Fk, удовлетворяющих оценке (2.11), 3) конечный набор номеров Ik = { 1 , 2 ,..., m_k} С N, точек {ek }iei _k С Tn положите.тьных чисел {Xk }iei_k- удовлетворяющих условиям 52 Xk = 1 и max {Xk | i ∈ I k

| i Е Ik} < к- для которьIX при всех k Е N справедливы выражения

Qk С Dk + (Y + ео)B 1(0), mk                 mk где Qk = ^Gk(ek)Xk, Dk = ^Fk(ek)Xk. (2.14) i=1                    i=1

Так как по условию отображения Gk, Fk ограничены на. T. а именно: Gk ( t ) С X и Fk ( t ) С X при всех t Е T. то и все множества. Qk i1 Dk. г,де к Е N. ограничены, точнее Q_k С Х и D_k С X. В силу свойства компактности подпространства K ( X ), состоящего из компактов, содержащихся в заданном компакте X. из последователыюстей {Q_k }k =1 ii {D_k}k =₁ можно выделить сходящиеся в метрике Хаусдорфа подпоследовательности. Без ограничения общности полагаем, что последовательности {Qk}_k =₁ ¹¹ {Dk}_k =₁ сходятся в K ( X ) к некоторым компактам Q Е co K ( X ) i i d Е K ( X ) соответственно. Поэтому из (2.14) в пределе получаем, что

Q С D + B y (0) .            (2. Li)

С другой стороны, из второго включения в (2.13) получаем, что Qk С co Dk + B_Y (0). Учитывая к тому же то, что последовательность { co Dk}k + сходится к co D в K ( X ), в пределе получаем включение

Q С co D + BY (0). (2.16) Выражения (2.15) и (2.16) возможны лишь в случае, когда D = coD. Покажем, что это не так, откуда, допущение о несправедливости нера- веиства (2.12) будет опровергнуто. Перегруппируем слагаемые в каждом Dk в (2.14) так, чтобы получить новый вид: Dk = этого полагаем

A k ⁺ ^ ⁺ A k . Для

Ak = к • X Fk ( ek ) Xk У p Е (1 ,к ) , i = Г p - 1 + 1

где натуральные числа r о = 0 < r 1 < r ₂ < • • • <

< rk = mk таковы, что справедливы неравенства Г р                Г р + 1                           _________

P Xk 6 p <  P Xk при лтобом p Е (1 , к — 1). Так i =1        ^k    i =1

как по построению max {Xk | i Е I_k} < 1, то такие числа r_p, г де p Е (1 , к — 1), существуют, причём справедлива оценка Ap С X. Осталось применить теорему 2.1 об усреднении, из которой следует, что D = co D. Теорема доказана.

Следствие 2.1. Пусть T — топологическое пространство, X — выпуклый компакт из равномерно гладкого банахова пространства E. Тогда для любого числа, е > 0 найдете я число v = = v(е, X) > 0 такое, что для любого многозначного отображения F: T ^ K (X), любого конечного набора точек {ei }iei С T и для любого конечного набора положительных чисел {Xi}iei, таких, что 52 Xi = 1 и max {Xi | i Е I} < v, справедливо i∈I неравенство h ( X(co F (ei)) Xi, X F (ei) Xi) <е. □ (2.17) i∈I                   i∈I

• III.    Интеграл Римана на отрезке для отображений в K (E)

Всюду считаем, что E — равномерно гладкое банахово пространство. Так как в метрическом пространстве K ( E ) были введены операции сложения и умножения на. действительное число, то мы вправе ввести интеграл Римана, на. отрезке для отображений F : [ a, b ] ^ K ( E ), как и для функций, через предел конечных сумм вида. (см. [15-17]):

m

X F ( ei )A ti, где ei Е [ ti— 1 ,ti ] , A ti = ti — ti- 1 , i =i                                                   (3.1)

a = 1 ₀ < 1 1 < • • • < t_m = b.

Однако пространство K ( E ) не является линейным и нормированным. Это не позволяет воспользоваться формально теорией интегрирования по Риману функций со значениями в банаховом пространстве, хотя общую схему рассуждений [18] в какой-то мере можно сохранить (ср. [5,9]).

Для построения интеграла. Римана, на. отрезке, как обычно, потребуется ввести понятие разбиения отрезка.

Римановым разбиением (или просто: разбиением) отрезка [ a, b ] называется конечная совокупность интервалов ш ([ a,b ]) = {T 1 ,T2,... ,Т_тш} , где Ti ⁽ ti- 1 , ti )- II a t о < t 1 < • • • < Рп_ш b - Причем точки ti, i Е (0 ,m ), будем называть точками разбиения ш ([ a, b ]). Диаметра,и разбиения ш ([ a, b ]) называется величина |ш ([ a, b ]) | == max {|Ti| | i Е Е (1 , т_ш ) } . где |Ti| = ti — ti- 1.

Определение 3.1. Отображение F: [ a,b ] ^ ^ K ( E ) называется ступенчатым, если существует такое риманово разбиение ш ([ a,b ]) отрезка [ a,b ]. что на. каждогi из интервалов Ti Е ш ([ a,b ]) отображение F постоянно.

Указанное в определении 3.1 ступенчатого отображения разбиение ш ([ a,b ]) называется допустимым для ступенчатого отображения F.

Будем различать ступенчатые отображения не только по их значениям, по и ио выбору допустимого разбиения.

Определение 3.2. Пара ( ш ([ a,b ]) ,F ), где F: [ a, b ] ^ K ( E ) — ступенчатое отображение, а ш ([ a, b ]) — допустимое для этого отображения разбиение отрезка [ a, b ], называется ступенчатой парой.

Определение 3.3. Прединтегралом Римана ступенчатой пары ( ш ([ a,b ]) ,F ), г де F: [ a,b ] ^

^ K ( E ), называется множество

j ( w ([ a,b ]) ,F ) [ a,b ]

mω dt = £f(^)iTil,  ^ e Ti, (3.2)

i =1

где w ([ a, b ]) = {T 1 , T 2 ,..., Tm ^ }.

Легко увидеть, что при отсутствии выпуклости значений F ( t ) для одного и того же ступенчатого отображения F, выбирая различные допустимые разбиения в формуле (3.2), можем получить разные значения сумм.

В свою очередь, если ступенчатое отображение F принимает лишь выпуклые значения, то формула. (3.2) дает один и тот же результат при любом выборе допустимых разбиений. В частности, для ступенчатого отображения F : [ a, b ] ^ ^ K ( E ) можно корректно определить интеграл от выпуклозначного ступенчатого отображения co F по формуле

Определение 3.4. Отображение F: [ a, b ] ^ ^ K ( E ) называется интегрируемым но Риману на [ a,b ], если оно компактно ограничено, т. е. существует компакт X e co K ( E ) такой, что F ( t ) e e K ( X )    Vt e [ a, b ]. 11 для любого e >  0

существует такая ступенчатая пара ( w ([ a, b ]) , G ), где |w ([ a,b ]) | < e. а отображение G: [ a,b ] ^ ^ K ( X ) таково, что справедливо неравенство ∗

J h (co F, co G ) dt 6 e.

[ a,b ]

Определение 3.4 эквивалентно существо

/

[ a,b ]

mω co Fdt = 2 co F (^) ITil, i =1

ξi ∈ Ti ,

(3.3)

ванию последовательности ступенчатых пар { ( wk ([ a, b ]) ,Fk ) }. г,де F^ [ a, b ] ^ K ( X ). к e e N, для которых последовательности диаметров {|wk ([ a, b ]) |} и верхних интегралов ∗

{ J h (co F, co Fk ) dt} сходятся к нулю при к ^ ж. [ a,b ]

Такая последовательность пар { ( wk ([ a, b ]) ,F_k ) }k =₁ называется аппроксимирующей последовательностью ступенчатых пар для интеграла. Римана, на. отрезке [ a, b ] отображения F.

где w ([ a, b ]) = {T 1 , T 2 ,..., Tm ^ } — любое допустимое разбиение отображения F.

В силу данной формулы (3.3) интеграл от выпуклой оболочки ступенчатого отображения как конечная сумма, выпуклых компактов есть выпуклый компакт в E, и для ступенчатых отображений F,G: [ a, b ] ^ K ( E ), очевидно, справедливы равенства. ( a e R¹):

Лемма 3.1. Пусть X e co K ( E ). Компактно ограниченное отображение F: [ a, b ] ^ K ( X ) интегрируемо по Риману тогда, и только тогда, когда.

для всякого числа e >  0 существует ступенча

j a (co F )

[ a,b ]

dt = a

j

[ a,b ]

co F dt,

(3.4)

тая пара. ( w ([ a, b ]) , G ). где отображеиие G; [ a, b ] ^ ^ K ( X )■ и ступенчатая (функция А : [ a, b ] ^ R₊ такие, что справедливы оценки |w ([ a, b ]) | < e, h (co F, co G ) 6 А 11 R Adt 6 e.                  □

[ a,b ]

Теорема 3.1. Пусть F: [ a,b ] ^ K ( E ) — интегрируемое по Риману отображение и { ( wk ([ a,b ]) ,F_k ) }k =1 — его аппроксимирующая по

У (co F + co G ) dt

[ a,b ]

/

[ a,b ]

co F dt +

j

[ a,b ]

co G dt.

Из формулы (3.3) для ступенчатого отображения F; [ a, b ] ^ K ( E ), очевидно, следует равенство опорных функций

s ( Р, У co Fdt )= У s ( p,F ) dt Vp e R n. (3.6) [ a,b ]                    [ a,b ]

Если рассматривать ступенчатую функцию f; [ a, b ] ^ E, то определение интеграла Римана для неё очевидным образом получается из формулы (3.3), если многозначное отображение таково, что каждое его значение состоит из одной ТОЧКИ ^{F (} ^i ) = ^{{f (} ^i ) ^}.

Следуя [18], получаем, что для вещественной ограниченной функции f > 0 на отрезке [a, b] верх-∗ ним интегралом Римана J fdt этой функции f [a,b] называется число

∗

У f dt = inf

[ a,b ]

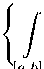
^ R¹

— ступенчатая, g

> f .

следовательность ступенчатых пар. Тогда, в прост

ранстве K ( E ) существует предел последователь

ности предиптегралов

R ( wk ([ a,b ]) ,Fk ) dt ” .

[ a,b ]                             ^{k =1}

являющийся выпуклым компактом, и этот предел

не зависит от выбора, аппроксимирующей последо-

ва.телыюсти ступенчатых пар.

¤

Доказательство. При любых m, k e N для ступенчатых отображений co F_m и co Fk выберем общее допустимое разбиение отрезка [ a, b ], и в силу соотношения (3.3), получаем

h

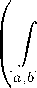
co F_m dt,

co F_k dt

[ a,b ]

I h (co Fm, co Fk ) dt

[ a,b ]

∗∗

6 j h (co F, co Fm ) dt + j

[ a,b ]                                    [ a,b ]

h (co F, co Fk ) dt.

Отсюда следует, что при т и к , стремящихся к бес

конечности,

величина, h     co Fm dt, J co Fkdt

[ a,b ]                 [ a,b ]

стремится к нулю.

тельпость интегралов

Следовательно,

{ R co Fkdt\ ^k [ a,b ]

∞ k=1

последова-фундамен

между собой (т. е. справедливо равенство)

тальна. и, в силу полноты метрического прост

ранства K ( E ), эта последовательность имеет предел в co K ( E ).

/

[ a,b ]

F dt =

[ a,b ]

co F dt.

□ (3 . 7)

Отметим, что все отображения Fk компактно ограничены в совокупности. В силу (3.2), (3.3) по

лучаем равенства.

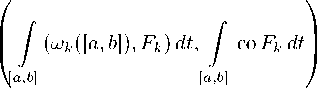
m ω_k           m ω_k

(3.6)

X Fk (£) Xk, X co Fk ( ^k ) Xk] i =1             i =1              /

Доказательство очевидно в силу доказательства теоремы, причем если { ( w_k ([ a, b ]) , F_k ) }k =₁ есть некоторая аппроксимирующая последовательность ступенчатых пар для F, то { ( w_k ([ a, b ]) , co F_k ) }k =₁ будет аппроксимирующей последовательностью ступенчатых пар для co F и, как показано в теореме, пределы последовательностей интегралов от них совпадают.

Следствие 3.2. Пусть отображение F: [ a,b ] ^ K ( E ) является ступенчатым. Тогда справедливо равенство

. | T ^k | ^r^ ^xk = b-a ■

Поэтому и по следствию 2.1 для любого числа. е > 0 найдете я число v = v (е) > 0 такое, что для всех номеров к. для кс>торых |wk ([a, b]) | < (b — a) v. величина (3.6) не превосходит числа (b — a)е. Так как по условию lim |wk([a,b])| = 0. то последо-k—>+се вательпость значений (3.6) стремится к пулю.

Это означает, что предел последовательности ∞ прединтегралов ( J (wk ([a, b]) ,Fk) dt> сущест-[a,b]                         k=1

вует и равен пределу последовательности интегра-

/

[ a,b ]

F dt = Xco F ( ^ ) iTil, ^ G Ti i =1

(3.8)

где w ([ a, b ]) = {T 1 ,T 2 ,... ,Тт _ш } — любое допустимое разбиение отображения F. □

Теорема 3.2. Пусть а G R¹, a F,G: [ a, b ] ^ ^ K ( E ) — два интегрируемых по Риману отображения, тогда aF и F + G также интегрируемы по Риману и для них справедливы формулы

лов J co Fk dt

[ a,b ]

Рассмотрим

∞

, t. e. k =1

выпуклому компакту.

/

[ a,b ]

aF dt = а

/

[ a,b ]

Две

F последовательности

{ ( Wk ([ a,b ]) ,Fk ) } -1

и

Тогда, последовательность

аппроксимирующие ступенчатых пар { ( wk ([ a,b ]) ,Gk ) } -1. nap ( w 1([ a,b ]) ,F 1).

j ( F + G ) dt

[ a,b ]

/

[ a,b ]

F dt,

F dt +

Gdt.

(3.9)

¤

[ a,b ]

( w 1 ([ a,b ]) ,G i). ( w 2([ a,b ]) ,F 2). ( w 2([ a,b ]) ,G 2). ■■

( Wk ([ a, b ]) , Fk ). wk ([ a,b ]) , Gk ) очевидно, также будет аппроксимирующей. Поэтому последовательность J ( w 1([ a,b ]) ,F 1) dt. J ( w 1 ([ a,b ]) ,G 1) dt.

[ a,b ]

R ( w 2([ a,b ]) ,F 2) dt. [ a,b ]

[ a,b ]

J ( w 2 ([ a,b ]) ,G 2) dt. [ a,b ]

•    •    •

должна, иметь предел. Это и означает,

что

∞

последовательности

I ^{R ( w}k ^{([ a,b ]) ,G}k ) ^dt [ a,b ]

R ( Wk ([ a,b ]) ,Fk ) dt [ a,b ] ∞

k =1

дел. Теорема доказана.

имеют одни общий пре- k=1

Доказательство. Равенство для aF в (3.9) очевидно. Пусть теперь { ( w_k ([ a, b ]) , F_k ) }k =₁ и { ( wk ([ a, b ]) ,G_k ) }е =₁ — аппроксимирующие последовательности ступенчатых пар для отображений F и G соответственно. В силу неравенства h (co( F + G ). co( F_k + G_k )) 6 h (co F, co F_k ) + + h (co G, co Gk ) получаем, что последовательность ступенчатых пар { ( wk ([ a, b ]) ,Fk + Gk ) }k =1, где разбиение w_k ([ a, b ]) содержит все точки разбиений wk ([ a, b ]) и wk ([ a, b ]), будет аппроксимирующей для отображения F + G. Из правого равенства в (3.7), взятого для отображений Fk и Gk, и в силу непрерывности операции алгебраической суммы Мин

Определение 3.5. Значение предела, указанного в теореме 3.1, называется интегралом Римана интегрируемого отображения F: [ a, b ] ^ b

^ K ( E ) и обозначасчся через JF ( t ) dt. J F dt. a                 [ a,b ]

или ( R ) R F dt.

[ a,b ]

Следствие 3.1. Пусть отображение F: [ a, b ] ^ K ( E ) интегрируемо по Риману, тогда и отображение co F: [ a,b ] ^ K ( E ) интегрируемо no Риману, причем интегралы Римана, от них равны

ковского в пределе получаем нижнее равенство в (3.9) для отображений F и G.

Следствие 3.3. Пусть выбраны числа a, b, c G G R¹. npiгаем a < b < c. Отображение F; [ a, c ] ^ ^ K ( E ) интегрируемо по Риману на [ a, c ] тогда, ii только тогда, когда, оно интегрируемо по Риману как на [ a,b ], так и на [ b, c ]. При этом справедливо равенство

/

[ a,c ]

F dt =

F dt +

F dt.

□ (3 . 10)

[ a,b ]

[ b,c ]

Доказательство. Для произвольного множества A определим характеристическую функ-

цию этого множества, по формуле

1 , если t е A.

0 , если t е A-

XA ⁽ t ) = |

Пусть отображение F интегрируемо по Риману на. отрезках [a, b] и [b, c]. тогда, на. отрезке [a,c] интегрируемы отображения F • х[a,b] и F • х(b,c], причем из равенства F = F • х[a,b] + F • X(b,c] и теоремы 3.2 следует интегрируемость по Риману отображения F на от резке [ a, c ] и равенство (3.10). Обратно, пусть F интегрируемо по Риману на отрезке [a,c] и пусть {Fk }k=1 — его аппроксимирующая последовательность и по-∗ следовательность J h(co F, co Fk) dt стремится к [a,c]

нулю при к ^ ж. Тогда очевидно существуют и стремятся к нулю последовательности интегралов ∗∗

J h (co F, co Fk ) dt и J h (co F, co Fk ) dt. т. с. oto- [ a,b ]                                       [ b,c ]

бражение F интегрируемо по Риману на отрезках [ a, b ] и [ b, c ].

Теорема 3.3. Пусть отображения F и G: [ a,b ] ^ K ( E ) интегрируемы по Риману. Тогда интегрируема по Риману функция h (co F, co G ): [ a, b ] ^ R+ и справедливо неравенство

Следствие 3.4. Пусть F: [ a,b ] ^ K ( E ) интегрируемо по Риману. Тогда, справедливо неравенство | | R F dtk 6 R kF|| dt.                   □

[ a,b ]                [ a,b ]

Доказательство следует из (3.11) и определения полунормы ограниченного множества, положив при этом, что G ( t ) = { 0 } при всех t е [ a, b ].

Теорема 3.4. Пусть отображение F: [ a,b ] ^ ^ K ( E ) интегрируемо по Риману. Тогда при любом p е E* опорная функция s ( p,F ): [ a, b ] ^ R¹ также интегрируема, по Риману и справедливо равенство

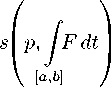
= У s ( p,F ) dt Vp е E*. □ (3 . 12) [ a,b ]

h

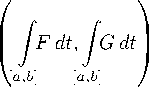
Ih (co F, co G ) dt. □ (3 . 11)

[ a,b ]

Доказательство. Пусть {Fk }k =₁ и {Gk}k =i — аппроксимирующие последовательности отображений F и G соответственно. Тогда последовательности { co Fk }k =₁ и { co G_k }k =₁ являются аппроксимирующими для отображений co F и co G соответственно. Из этого и из неравенства |h (co F, co G ) — — h (co Fk, co Gk ) | 6 h (co F, co Fk ) + h (co G, co Gk )

следует стремление к нулю

∗ тслыюсти < J |h(co F, co G) [a,b]

при к ^ ж.

Таким

вателыюсть ступенчатых gk ( t ) = h (co Fk ( t ) , co Gk ( t )). мирующей для функции f ( t )

числовой последова-— h (co Fk, co Gk) | dt j образом, последо-фуикций gk.   где является аппрокси-= h(coF(t), co G(t)).

Доказательство аналогично доказательству теоремы 3.3. Пусть {Fk}k=1 — произвольная аппроксимирующая последовательность для F и вектор p е E* зафиксирован. В силу свойств хаусдорфовой метрики (см., например, [19]) справедливо неравенство |s(p, F) — s(p,Fk) | 6 6 kpkh(co F, co Fk), откуда числовая последо-∗ вателыюсть J |s(p,F) — s(p,Fk) | dt стремится [a,b]

к пулю при к ^ ж. Следовательно, последовательность функций {s ( p,F_k ) }k =1 является аппроксимирующей для функции s ( p, F ), т. е. функция t ^ s ( p, F ( t )) интегрируема по Риману и справедливо равенство J s ( p, F ) dt = [ a,b ]

= lim J s ( p,F_k ) dt. В силу непрерывности опор- k→∞

[ a,b ]

пой функции как функции множества, а. также в силу равенства. (3.5) для каждого отображения co Fk, получаем в пределе равенство (3.5) для отображения F , откуда в силу равенства (3.7) получаем (3.12).

Следствие 3.5. Пусть отображения F и G: [ a, b ] ^ K ( E ) интегрируемы по Риману и удовлетворяют условию: F ( t ) С G ( t ) при всех t е [ a,b ]. Тогда, справедливо включение

j

[ a,b ]

F dt ⊂

[ a,b ]

Gdt.

¤

Поэтому эта функция f интегрируема по Риману и lim J h (co F_k, co G_k ) dt = J h (co F, co G ) dt. ^k ” [ a,b ]                                     [ a,b ]

Кроме того, по аналогии с доказательством тео

Доказательство. Из условия следует, что для любого p е E* справедливы неравенства s ( p, F ( t )) 6 s ( p,G ( t )) при всех t е [ a, b ].

что по свойствам интегрируемых функций вле

ремы 3.1 на. общем допустимом для ступенчатых отображений co F_k и co G_k разбиении получаем

чёт неравенство для интегралов J s ( p, F ) dt 6 [ a,b ]

неравенство

6 j s ( p, G ) dt. По теореме 3.4 получаем нера-[ a,b ]

Г h I co

[ a,b ]

Fk dt. /со Gk d t) 6/ h ⁽c° Fk, . Gk ) dt. [ a,b ]                     [ a,b ]

веиство s p, J F dt [ a,b ]

6 s p, J G dt . Отсюда. [ a,b ]

в силу произвольности p е E*, выпуклости ин

Переходя к пределу по к ^ ж, в силу равенства. (3.7) получаем неравенство (3.11).

тегралов Римана, (теорема. 3.1) и свойств опорных функций (см, например, [19]) получаем искомое

включение для многозначных интегралов.

Покажем наконец, что в равномерно гладком банаховом пространстве E интеграл Римана может быть представлен как предел интегральных сумм Римана. (3.1).

Лемма 3.2. Пусть число у < + го, множества X Е coK(E). Q Е coK(X) и отобу>ажеиие F: [а, в] ^ K(X) ( где а < в) таковы, что h(Q, co F(t)) 6 y Vt Е [а, в]• (3.13)

Тогда для любого числа е >  0 найдется число П = п ( е ) >  0 такое, что для любого разбиения ш ([ а, в ]) = {t о- 1 1 tm „ } отреузка [ а, в ] с диаметром |ш ([ а, в ]) | = max {ti — ti- 1 | i Е (1 , т_ш ) } 6 п и при любом выборе точек ei Е [ а, в ], i Е (1 ,т_ш ), справедливо неравенство

Покажем, что 5 = min { 8 ^ j ^ ^ ^ , п ( е 1) } обладает необходимым свойством, дающим (3.15). В самом деле, пусть ш ([ a,b ]) = {t 0. 1 1..... t_m} — произвольное разбиение отрезка [ a, b ], причем max {ti — — ti- 1 | i Е (1 ,m ) } 6 5. Пусть выбраны произвольные точки ^i Е [ ti- 1 , ti ]. Через ш* ([ a, b ]) == {t 0, t 1, .... tk} обозначим такое j Разбиение отрезка [ a, b ]. которое получится объединением всех точек разбиений ш ⁰([ a,b ]) 11 ш ([ a,b ]). Тогда точки {^*}j _₁ определим из равенства ^* = ^i, г де i Е (1 , m ) такое, что [ ti- 1 , ti ] D [ t*- 1 , t* ]. Обозначим Д t* = t* — — t*- 1 и Д ti = ti — ti- 1. Оценим искомое расстояние (3.15) следующим образом:

mω h ( Q, ill (F(^) Д

^— ti- 1

β-α

6 y + е. □ (3 • 14)

m

/ F dt, X F(^i)Дti i=1

a,b ]

Доказательство. Данная лемма, является простым следствием теоремы 2.2, в которой следует выбрать T = [ а, в ]; G ( t ) = . t - t

= Q ; Xi = в - _а • По указанной в теореме 2.2 функции v ( е ) выб)>ать п ( е ) 6 v ( е )( в — а ).

Теорема 3.5. Пусть отображение F : [ a, b ] ^ ^ K ( E ) интегрируемо по Риману. Тогда для любого числа, е >  0 можно на.йти число 5 = 5 ( е ) > >  0, обладающее следующим свойством: для любого разбиения ш ([ a, b ]) = {t ₀, t 1, ... , tm ^ } отрезка [ a, b ]. диаметр которого и с превосходит числа. 5. и при любом выборе точек ei Е [ ti- 1 , ti ] справедливо

6 h

Fdt,

G dt ^I +

[ a,b ]

[ a,b ]

+ h I I co Gdt, XX F ( e* )Д t* I + у a,b ]            j =1

km

X f (e* )Д-*,^f (ei )Д ti j=1           i=1

(3 • 17)

неравенство

m

/ F dt, 'X F ( ei )Д ti I 6 е.

i =1

a,b ]                            /

□ (3 • 15)

По теореме 3.3 получаем

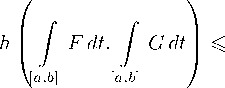
Доказательство. Пусть в силу компактной ограниченности F множество X Е co K ( E ) таково, что F; [ a,b ] ^ K ( X ). Зафпкац>уем число е >  0. По лемме 3.1 существуют ступенчатые отображение G : [ a,b ] ^ K ( X ) и фу1пения X : [ a, b ] ^ R+ такие, что h (co F, co G ) 6 X ii J Xdt 6 |. Обозна-[ a,b ]

ним через y ₀ = a < y 1 < • • • < y_N = b точки разбиения ш ⁰([ a, b ]), являющегося общим допустимым для ступенчатых отображения G и функции X.

j h (co F, co G ) dt

[ a,b ]

[ a,b ]

λ dt 6

ε

4 •

Суммируя неравенства (3.16) no s , получаем

Обозначим Д ys = ys — ys- 1. а чсрез Gs i1 Xs —

соответствующие значения co G ( t ) и X ( t ) при t Е

Е ( y_s- 1 , ys ), s Е (1 , N ). Так как справедливо не

I / co Gdt, X( F ( e* )Д t* )l 6

[ a,b ]             ^{j =1}

⁶ XX (4( b — a ) ^{+ Xs} ) ^Д y^s = 4 ⁺ / ^{Xdt 6} 2 • ^{s =}                                             [ a,b ]

равенство h ( Gs, co F ( t )) 6 Xs щ hi t Е ( ys- 1 , ys ).

то по лемме 3.2 для числа е 1 =

ε

4( b — a )

найдётся

число п ( е 1) >  0 такое, что для всякого разбие

ния отрезка [ y_s- 1 ,y_s ] с диаметром, не превосходящим числа, п ( е 1)- и при любом выборе точек ^j Е Е ( y_s- 1 ,y_s ) справедливы неравенства

h ( Gs Д ys, XX F ( ^j )Д ts ) 6

j =1

⁶ (4( 6 ^ ^{+ Xs} ) ^Д ys

Vs Е (1 ,N ) •

(3 . 16)

m

Множество ^2 F ( ei )Д ti отличается от множества i =1

k

F ( e* )Д t* лишь по тезi слагаемым i. для кото- j =1

рых интервалы ( ti- 1 , ti ) содержат точки из разбиения ш ⁰([ a,b ]). Для любе)го номера, s Е (0 , N ) обозначим через j ( s ) такой ном ер от 0 до к, при котором ys = t* ( s )■ г,де ys ^{Е ш 0([ a,b ])}. t* ( s ) ^{Е ш}* ^{([ a,b ])}. Пусть S* := {s Е (1 , N ) | y_s Е ш ([ a,b ]) } . Для любого номера, s Е S* найдёте я номер i ( s ) Е (1 ,m ) такой, что ^Д ti ( s ) = ^Д t* ( s )^+Д t* ( s )+1 ^{11 e}i ( s ) = ^e* ( s ) =

= js)+1. Учитывая это, для третьего слагаемого в (3.17) получаем оценку km

Е F ( j )A t^F ( ^ )A ti I 6

j =1             i =1          /

6 X h ( F ( j. ))^A j. ) + F ( j. )Ж^А t*. )+i ■ s ∈ S ^∗

ε

F ( ^ ( _s ))A ti ( _s >) 6 2 N5kXk 6 4 . Теорема, доказана.

• IV.    Необходимые и достаточные условия интегрируемости по Риману

В этом параграфе полагаем, что E — сепарабельное банахово пространство, у которого E* также является сепарабельным пространством.

Теорема 4.1. Для того чтобы компактно ограниченное отображение F : [ a, b ] ^ K ( E ) было интегрируемо по Риману, необходимо, чтобы отображение co F было непрерывно почти всюду на [ a,b ].                                                           □

Доказательство. Пусть F интегрируемо по Риману на [ a,b ], тогда по теореме 3.4 при всяком p е E* функция t ^ s ( p, F ( t )) интегрируема по Риману. По известному (см., например, [18]) условию интегрируемости по Риману функций из того, что для каждого p е E*, ||pk = 1, функция t ^ ^ s ( p, F ( t )) интегрируема, на. [ a, b ] по Риману, следует, что опа. непрерывна, почти всюду. В свою очередь в сепарабельных пространствах это означает, что отображение co F непрерывно почти всюду на [ a,b ]. Теорема доказана.

Для доказательства, достаточных условий интегрируемости по Риману определим два. понятия колебаний отображения F: R¹ ^ K ( E ) на множестве A С R¹ и в точке t е R¹ по следующим формулам:

О( F ; A ) = sup {h ( F ( t 1) , F ( t 2)) | t 1 ,t 2 е A} ; (4.1)

О _F ( t ) = inf { 0( F ; ( c, d )) | c, d е R¹ , c

(4-2) Очевидно, что отображение F : R¹ ^ K ( E ) непрерывно в точке t о е R¹ тогда и только тогда, когда О F ( ‘ 0) = 0.

Для любого 5 >  0 также определим на отрезке T = [ a, b ] множество

Is ( F ) = {t е T | О f ( t ) >  5}.        (4.3)

Легко показать, что множество Is ( F ) замкнуто.

где Оi = 0(co F, [ ti- 1 ,ti ]) (см. (4.1)).               □

Доказательство. Пусть выполнены условия леммы и ше ([a, b]) — указанное там разбиение от резка. Определим ступенчатые отображение G: (a, b] ^ co K(E) и фуггкцию А: (a, b] ^ R1. так, что G(t) = coF(ti) 11 А(t) = Оi при всех t е (ti- 1 ,ti]. i е (1, k). Очеви,дно. что h(G(t), co F(t)) 6 А(t) при k t е (a,b]. Кроме того, f Adt = 52 (‘i - ti- 1)0i 6 [ a,b ]           i=1

6 е . В силу леммы 3.1 получаем, что отображение F интегрируемо по Риману.

Теорема 4.2. Пусть компактно ограниченное отображение F: [ a,b ] ^ K ( E ) таково, что отображение co F непрерывно п<зчти всюду на. [ a,b ]. Тогда F интегрируемо по Риману на. [ a,b ].     □

Доказательство. Пусть е >    0,

M = sup {kF (t) k | t е [ a,b ]} 6 ||X||. О * = 0(co F, [ a,b ]) (cm. (4.1) ). Очевидно, что О * 6 2 M < + го. Пусть I* — множество точек разрыва отображения co F 11 а [a, b]. Согласно условию теоремы мера Лебега множества I* равна нулю. Это значит, что для любого п > 0 множество I* можно покрыть не более чем счётной системой от крытых интервалов с суммарной длиной меньше П- Выбираем п таким, чтобы О * п 6 ^- Выберем

ε

2( b — a )

число 5 =

и рассмотрим множество точек

Is(F) (см. (4.3)), колебание в которых не менее, чем данное 5. Так как Is (F) С I*. то множество Is(F) также покрывается этой системой интервалов. В силу компактности множества Is (F)

выберем из указанной системы интервалов ко нечную совокупность интервалов, покрывающих Is(F), причём сумма их длин и подавно меньше П- Построим разбиение ш([a,b]) = {t0. 11.....tk} отрезка [a, b] такое, чтобы прежде всего в него входили все концы выделенного конечного множества интервалов, покрывающих Is (F). Кроме того, потребуем, чтобы оставшаяся вне этих интервалов часть отрезка [a, b] была разбита точками из ш([a,b]) на. столь мелкие части [ti- 1, ti]. чтобы колебание отображения co F на каждом из них не превышало 5. Для построенного разбиения k

ш ([ a,b ]) рассмотрим сумму вила. 52 ( ‘i - ti- 1)О i. i =1

где О i = О(co F, [ ti- 1 , ti ]). Разобьём эту сумму на две группы слагаемых X = Х1 + Х₂, где к первой из них отнесены индексы i е (1 , k ), для которых отрезки [ ti- 1 , ti ] ие содержит интервалы из конечного покрытия для Is ( F ), ко второму — остальные. Оценим каждое слагаемое:

^X1⁽ ‘i - ‘i- 1^)О i ^{6 5 ( b — a} ) ⁶ ^ , X2( ti — ti- 1)о i 6 о * п 6 е.

В силу леммы 4.1 это означает интегрируемость F на. [ a, b ].

• V.    Заключение

В данной статье мы разобрали лишь простейший случай интеграла. Римана, от многозначного отображения на. отрезке. Указанные результаты перенесены автором и па. случай интеграла. Римана, от многозначного отображения, заданного на. компактном топологическом пространстве с мерой, со значениями в пространстве компактов из равномерно гладкого банахова, пространства. Показано, что в случае, когда, мера, заданная па. компакте, является непрерывной (неатомарной), то результаты получаются аналогичные случаю отрезка. Если же мера, не является непрерывной, то интеграл Римана, не обязан быть выпуклым компактом и условия интегрируемости по Риману многозначного отображения принимают другой вид. Эти и другие результаты будут описаны в моей книге «Многозначный анализ и дифференциальные включения», которую я планирую опубликовать в 2012 году.