Интегрирование в элементарных функциях двунаправленного уравнения распространения импульсов в оптических волокнах для степенной нелинейности

Поле оптического импульса, распространяющегося в одномодовом волоконном световоде, поддерживающем состояние линейной поляризации, имеет вид [1]

E ⁽ r , t ) = e x F ⁽ x , y ) A ⁽ z , t )exp { i ( ^р o z -to o t ) } ,       (1)

где F ( x , y ) - обычно гауссовская функция вида exp{-( x ² + y ²)/ w ²} с характерным размером моды w , A( z , t ) - комплексная огибающая импульса, to o - несущая частота, в _o = to_on ( to _o )/ c - центральное волновое число. Для огибающей оптического импульса выведено [2] уравнение

/дА о дА^   1 д2А р, д2А i — + В. — +---— —- +

I д z    ¹ д t J 2 р _o дz ² 2 д t ²                    (₂)

+АР(|А|2) А = 0, названное расширенным уравнением распространения, которое существенно отличается от традиционного, называемого основным уравнением распространения [1], наличием второй производной по координате. Здесь р| = 1/vg - величина, обратная групповой скорости, р2 - дисперсия групповой скорости, Ар (| А |2) - нелинейная поправка к постоянной распространения моды в линейном приближении. В области прозрачности волновода Ар является вещественной функцией.

В [3] показано, что для солитоноподобных решений вида

А(z, t) = R(z,t)exp{iqz} ,(3)

где R - действительная функция, а q - произвольный параметр, функция R определяется двумя квадратурами:

11 -Рор2v2 Г_______________dR=

V   2р о       (q + q 2/2р o) R2 - B (R2) + C1(4)

= z ^- z o ^- vt ,

R ²

B (R2) = Г Ар(I)dI,(5)

где (-z0) и C - произвольные постоянные, а v = Vg (1+q / ро).(6)

Отметим, что при q / р ₀ = -1 квадратуры (4) и (5) определяют стоячую волну.

Таким образом, формулы (3), (4), (5) определяют трёхпараметрическое семейство решений уравнения (2). Если требуется найти локализованные решения, то постоянную C ₁ следует положить равной нулю. Действительно, если потребовать, чтобы функция R и её первые производные на бесконечности обращались в ноль, то по правилам дифференцирования неявных функций из (4) следует обращение произвольной постоянной в ноль.

Целью настоящей работы является нахождение локализованных решений уравнения (2) в элементарных функциях для степенного типа нелинейного отклика Ар ( R ²) среды на внешнее гармоническое возмущение.

Основной формализм

Если обозначить для краткости p = q (1 + q /2 р о ),                                  (7)

то формулу (4) можно переписать в виде

I /   d R     ₂ =^,

^J R 71 - B ( R²)/ pR²

где ^ = A h ² p ^{р 0} 2 ⁽ z ^- z o ^- vt ) . ⁽⁹⁾ X ^{1 -р} o ^р 2 ^V

Формула (8) в неявном виде определяет функцию R ( ^ ). Если интеграл в левой части (8) вычисляется в элементарных функциях и полученное выражение обратимо, то R = R ( ^ ) выражается в элементарных функциях. Если же после интегрирования получаем необратимое (трансцендентное) уравнение, то имеем обратную функцию ^ = ^ ( R ). В теории дифференциальных уравнений решения, записанные в виде прямой или обратной функции, равноправны. Если же интеграл в левой части (8) не выражается в элементарных функциях, то имеем ^ , выраженное в специальных функциях.

Если интенсивность вводимого излучения I = R ² невелика, то можно воспользоваться разложением функции нелинейного отклика Ав ( I) в степенной ряд [1]

Ар ( I ) =П 1 1 + П 2 1 ² +П з 1 ³ +•••                  (10)

и ограничиться первым отличным от нуля членом. Нелинейность вида Ав = n11 называется керровской. Если же функция Ав (I), рассматриваемая на всей чи- словой оси, имеет в нуле экстремум, то разложение в степенной ряд начинается со второй степени интенсивности. Нелинейность вида Δβ = η2I 2 называется некерровской. И тот и другой типы нелинейности являются степенными функциями с целым показателем, и интеграл в (8) для этого случая вычисляется в явном виде. Более того, вычисляется интеграл для любой степенной зависимости I α.

Итак, положим ∆β ( I ) = η I ^α . Тогда по формуле (5) находим B ( R ²) = ( η /( α + 1)) R ^{2 α +2}. Подставляя это выражение в (8), получим

пренебрежимо мала по сравнению с β0, то из (7) и (15) находим

J

R 1-

η R _{2 α} ( α+ 1) p

=ξ.

Интеграл в левой части этого выражения вычисляется подстановкой u = 1/ R . В результате имеем

1 ^f 1 I ( a+ 1) p ^J

- Arch               = ξ .a (R aV n J

Обращая последнее уравнение, находим

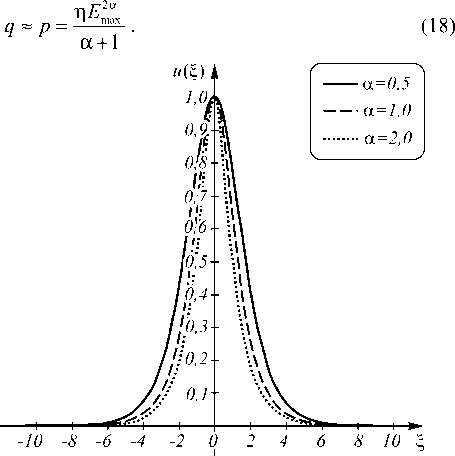
Рис. 1. Графики функции u = R / E _max для различных показателей степени α

R=

( α+ 1) p

η

ch ^{1/ α} ( αξ ) .

Перейдём от параметра p , который формулой (7) связан со свободным параметром q , к новому свободному параметру E max , для чего обозначим

(α+1)p η

к

E max ,

где E _max – пиковое значение напряжённости. Отсюда

p ₌ η E m ^{2 α} ax α + 1

и формула (13) принимает вид

R=Emax/ch1/α(αξ), где с учётом (9)

ξ=       2 ^{β o η E m2 α ax}     ( z - z - vt ) .

(1 - β o β 2 v ²)( α + 1)       ^o

Таким образом, формулы (16), (17), (3) и (1) в явном аналитическом виде решают задачу описания оптического поля в одномодовых волоконных световодах, поддерживающих состояние линейной поляризации. Примечательно, что это описание применимо в равной степени как к случаю керровской нелинейности, так и к случаю некерровской нелинейности.

Можно легко построить графики решений в относительных единицах для любых показателей степеней (рис. 1).

Для довершения полноты картины остаётся только выразить свободный параметр q через пиковое значение напряжённости E max .

Из (1) и (3) следует, что q является поправкой к центральному волновому числу β 0 . Если эта поправка

В противном случае следует решить квадратное уравнение, получающееся из (7) и (15):

qmax

+ q -

2βoα+

Его решение

q = βo

f-1 ±

= 0.

1+2nEmL J в o (a +1) J

в отличие от (18) может принимать как положительные, так и отрицательные значения.

Заключение

Таким образом, в явном аналитическом виде решена задача описания оптического поля в одномодовых волоконных световодах, поддерживающих состояние линейной поляризации, при произвольной степенной нелинейности. Как частный случай сюда входит широко применяемая [4– 6] модель с керровской нелинейностью.

Работа выполнена при государственной поддержке Министерства образования и науки РФ в рамках реализации мероприятий Программы повышения конкурентоспособности СГАУ среди ведущих мировых научно-образовательных центров на 2013–2020 годы.