Интегрированная модель мобильной роботизированной платформы

Научно-образовательный центр (НОЦ) «Инженерия будущего» – это межрегиональное объединение вузов 6 субъектов Российской Федерации (Самарской, Пензенской, Тамбовской, Ульяновской, Астраханской областей, Республики Мордовия), призванное объединить науку и реальный сектор экономики1. Целью НОЦ является достижение мирового лидерства в научно-технологическом развитии и подготовке кадров по направлениям деятельности центра.

Одним из таких направлений является агрокибернетика. Комитет «Умное агро» НОЦ разрабатывает цифровую мультиагентную систему. Система включает ряд сервисов для агропредприятий, разработчиков и производителей сельскохозяйственной техники.

В частности, сервис автономизации техники решает задачу беспилотного управления роботизированными транспортно-технологическими системами в контексте более общих задач, решаемых комитетом и направленных на повышение эффективности точного, почвозащитного и ресурсосберегающего земледелия. Среди основных задач такого типа следует указать следующие:

– панорамное гиперспектральное и 3D-сканирование объектов агроценоза;

– выполнение типовых технологических операций (химическая и механическая обработка растений, сбор и сортировка урожая фруктов и овощей с сопутствующим контролем качества на основе анализа гиперспектров и полученных вегетационных индексов);

– формирование виртуальных моделей для объектов агроценоза и ассоциативных двунаправленных связей между физическими (натурными) и виртуальными объектами;

– комбинированное траекторное управление мобильными системами с использованием современных методов навигации и позиционирования.

Для решения указанных задач необходима транспортно-технологическая автономная роботизированная платформа, отличающаяся маневренностью, высокой точностью управления и позиционирования.

Проект роботизированной платформы включает несущую систему, ходовую часть, систему торможения, управления, очувствления, а также робота-манипулятора и технологический блок. Проект реализуется в виде интегрированных CAx-моделей, предусматривающих анализ и оптимизацию проектных решений. При этом непременным требованием к проекту в целом является возможность глубокой интеграции всех программных, аппаратных модулей и CAx-моделей. CAx-модели формируются в базовой CAx-среде (SolidWorks) с использованием разработанного в рамках проекта программного обеспечения, расширяющего и дополняющего штатный функционал базовой системы в части задач синхронного управления мобильным роботом (физическим объектом) и его виртуальной CAx-моделью.

Таким образом, целью работы является построение киберфизической робототехнической системы как сервиса, обеспечивающего автономизацию сельскохозяйственной техники. При этом открытый программно-аппаратный интерфейс обеспечивает возможность интеграции платформы в базовую муль-тиагентную киберфизическую систему в качестве агента.

Обзор литературы

Задача автономизации техники является сложной, многодисциплинарной и решается, как правило, для множества разных, но взаимосвязанных объектов (агентов), имеющих единую систему управления. При этом одним из аспектов автономизации является ки-берфизическая интеграция данных единой цифровой платформы с объектами техники, которые рассматриваются как агенты этой базовой мультиагентной системы [1]. Этот факт предполагает взаимодействие не только агентов техники друг с другом, но еще и с агентами других типов (физических, химических, биологических) [2].

В одной из работ приведен всесторонний анализ структуры, технологий и инструментов, необходимых для реализации киберфизических систем в области интеллектуального агропредприятия в сравнении с аналогичными промышленными комплексами [2]. Общей особенностью этих систем является глубокая интеграция физических и виртуальных компонентов. При этом под виртуальными компонентами понимаются 3D- (CAx: CAD/ CAE), математические и программные модели, обладающие достаточной степенью адекватности физическим объектам [3].

Для построения мультиагентных робототехнических систем необходимо решить задачи траекторного управления, 612

Том 31, № 4. 2021

которые сводятся к выводу робота на заданную траекторию из произвольного положения и стабилизации движения по данной траектории.

Среди всего многообразия методов решения этих задач следует указать следующие основные методы: скольжение (sliding / слайдинг), обратный обход интегратора (back-stepping / бэкстеппинг), пропорционально-дифференциально-интегральное регулирование ПИД (proportional-differential-integral control PID) и линеаризация обратной связью (feedback linearization).

Скользящие методы обеспечивают сходимость за конечное время, но отличаются сингулярностью. Бэкстеп-пинг и ПИД-регулирование на практике не допускают аналитическую форму представления и сложны в реализации. Различные модификации этих методов направлены, как правило, на преодоление указанных недостатков [4]. Эту же цель преследуют многочисленные комбинированные методы, которые в последнее время явно превалируют в научной литературе. В работах обоснован комбинированный метод, который сочетает в себе пропорциональноинтегральное (ПИ / PI) управление со слайдингом [5], а также слайдинг с бэк-степпингом [6; 7].

Наше исследование затрагивает ту же проблему, что и ряд работ иностранных коллег [8–10]. При проведении экспериментов были использованы методы, описанные в других статьях [11; 12]. Особое место в исследованиях последнего времени занимает проблема формирования двунаправленных связей между реальным объектом (роботом или его натурной моделью) и его виртуальной моделью. Эта проблема хорошо описана в контексте управления мобильными роботами [13–15]. Также проведен всесторонний сравнительный анализ методов управления мобильными роботами [16].

Технологии и средства механизации сельского хозяйства

В данной работе для траекторного управления используется метод точной линеаризации замыкающей нелинейной обратной связью, делающей рассматриваемую систему линейной [17]. Метод является отечественной разработкой и отличается непрерывностью управления, задается аналитически, невосприимчив к вибрациям (чатте-рингу). При этом полученные стабилизирующие обратные связи обеспечивают экспоненциальное убывание заданной нормы отклонения от целевой траектории.

В пространстве «расстояние до траектории – ориентация» определены области притяжения для выхода на заданную траекторию с установленными показателями экспоненциальной устойчивости и получены управления для стабилизации по прямолинейному пути, по дуге окружности и составным траекториям, сформированным из отрезков прямых и дуг окружностей [17]. Аналогичная задача решена для целевой кривой, заданной параметрически с учетом динамики рулевого привода [18], в работе Л. Б. Рапопорта – для кривой, заданной явно аналитически [19], а в другом исследовании – для криволинейного пути с учетом неровностей поверхности движения [20]. Были рассмотрены варианты замены переменных для кинематической модели, приводящие к точной линеаризации уравнений движения. При этом отмечено, что ключевой проблемой для рассматриваемой задачи является определение расстояния от произвольной точки до целевой кривой [21]. Выполнен анализ результатов, полученных на основе законов управления, синтезированных с помощью разных канонических представлений [22].

Материалы и методы

В качестве базовой транспортной системы рассматривается самоходная база «Туман 1-М» индустриального партнера НОЦ «Пегас-Агро» (рис. 1), эксплуатационные параметры которой являются достаточными для размещения технологического оборудования, разрабатываемого в рамках проектов НОЦ «Умное агро», а также систем энергоснабжения2 [23].

В качестве модели шасси используется универсальная параметрическая CAD/CAE-модель (SolidWorks), разработанная авторами. Она легко адаптируется для разных проектных решений «Пегас-Агро» и предусматривает следующие виды компоновки: двухосевую и трехосевую, заднеприводную, переднеприводную и полноприводную. Модель оснащена одноосевым, двухосевым и дифференциальным управлением с учетом угла Аккермана [9; 24].

На рисунке 1 показаны варианты как двухосевой, так и трехосевой компоновки. Заметим, что для решения задачи траекторного управления существенное значение имеют лишь величины L (колесная база) и H (размер колеи), которые определяются так, как показано на рисунке 1.

В сформированную таким образом CAD/CAE-модель на несущие оси каждой из четырех подвесок установлено по два виртуальных мотора (рис. 1). Первый ( Motor_i j ) передает крутящий момент в вертикальной плоскости непосредственно на движитель и моделирует работу мотор-колеса. Второй мотор ( Drive_ij ) передает крутящий момент в горизонтальной плоскости и моделирует работу системы управления на базе шагового (серво) двигателя. Работу системы управления иллюстрирует видеоролик³.

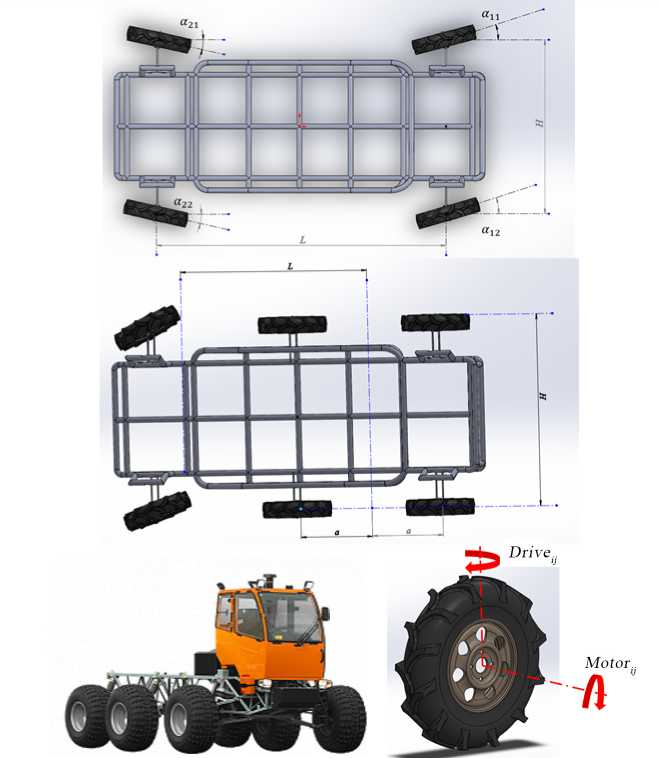
Р и с. 1. Самоходная база «Туман-1М» и модель компоновки для шасси робота

F i g. 1. Fog-1M self-propelled base and layout model for robot chassis

Motor_i j , Drive_i j установлены попарно на каждой подвеске и обеспечивают универсальность модели мобильного робота для наиболее общего случая его компоновки и управления ( i = 1, 2, j = 1, 2: индекс i соответствует номеру оси, индекс j – позициям «справа» и «слева» соответственно).

Управляющими параметрами являются угловые кинематические характеристики и углы поворота вокруг вертикальных осей для колес, отвечающих 614

за управление роботом. Таким образом задается угол Аккермана и моделируется функция механического дифференциала. При этом программный модуль допускает возможность адаптации к различным вариантам компоновки, а сама модель имеет иерархическую структуру, исключающую упругие и демпфирующие элементы на стадии решения задачи траекторного управления, что существенно снижает вычислительные затраты. Так, в случае

Технологии и средства механизации сельского хозяйства

классического варианта в качестве целевой точки рассматривается срединная точка задней оси с координатами x_c и y_c , ориентация робота задается углом θ между центральной осью платформы и осью x . Рассматривается движение робота без проскальзывания. Углы поворота передних колес α ₁ и α ₂ (рис. 1), отвечающие за ориентацию робота, определяются из соотношений:

tg ( « 1 ) =-

uL uH ‒ для внутренней

—

2 траектории,

mL tg (a2) - ——^ - для внешней 1 + -— траектории, где u – мгновенное значение кривизны траектории, описываемой целевой точкой [17]. Во всех других случаях компоновки актуальные параметры управления автоматически связываются с кривизной u.

Уравнения движения робота имеют следующий вид:

x c = vc cos9, yc - Vcsin9,

9 = vcu, где vc = ||Vc|| при движении вперед; vc = -||Vc|| при движении задним ходом; Vc – вектор мгновенной скорости целевой точки.

Результаты исследования

Ниже приведены результаты для моделирования траекторного управления для различных траекторий.

Случай движения по прямой

Для прямолинейной траектории, проходящей через начало отсчета под углом β к оси x необходимо выполнить преобразование координат:

^ - x c cos p + y c sin p ,

7 = y c cos p - x c sin p ,

/ - 9 - p.

Как показано в работе Л. Б. Рапопорта, управление вида

(          ^

21 + A2 z. -----------------321(1+ z32)2 J

где z ₂ = η , z ₃ = tg ψ , обеспечивает экспоненциальную скорость убывания z ₂ и z ₃ с показателем – λ [17].

На рисунке 2 показаны результаты численного эксперимента для некоторого произвольного начального положения робота и β = 10°, λ = 1, а видеоролик демонстрирует процесс стабилизации во времени⁴. При этом учитывались ограничения на углы поворота передних колес, то есть управление было задано в виде

(          ^

21 + A2 z^ u =" su ----------32- ,

1 ( 1 ⁺ z 32 ) 2 )

где su = [-u при u ≤ -u, u при |u| < u u при u ≥ u], где u – ограничение на кривизну траектории, связанное с ограничениями на поворот передних колес.

Р и с. 2. Результаты численного моделирования для вывода и стабилизации движения робота по прямолинейной траектории

F i g. 2. Results of numerical simulation to bring and to stabilize robot motion along straight path

Случай движения по дуге окружности

Дуга окружности задается центром x ₀, начальной точкой x_b , радиусом R и углом сектора. Обозначим также угол τ между осью x и радиусом-вектором X_c – X ₀ [17]. Тогда

демонстрируются для некоторого произвольного начального положения робота, параметры которого считываются с виртуальных сенсоров. Видеоролик демонстрирует процесс движения5.

П = ^(xc - x0 )2 + (Ус - У0 )2, £ = tR, / = 6 + т, Z1 = ^, z 2 = Л - R, z3 = tg^.

Аналогично (1), (2) управление может быть выбрано в виде

u - - 5

(J +    1 + z.

R ³

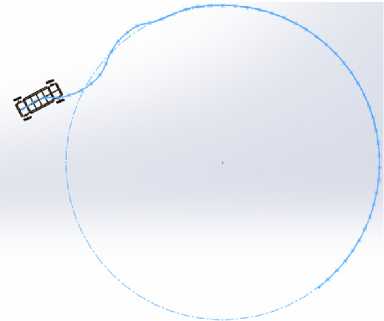
Р и с. 3. Результаты численного моделирования для вывода и стабилизации движения робота по окружности

F i g. 3. Results of numerical simulation to bring and to stabilize robot motion along arc path

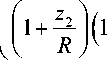
⁺ z 32 ) ²

V

где s _u определяется по-прежнему аналогично (2) [5].

На рисунке 3 показаны результаты численного эксперимента при λ = 1, X ₀ = (10, 20) м, заданном радиусе окружности R = 12 м. Результаты

Случай движения по сплайну

Введем следующие обозначения: C – текущая позиция робота; A – ближайшая к ней точка на целевой

траектории; O – мгновенный центр кривизны целевой траектории в точке A ; OA = R ( s ) = 1 / s ; k ( s ) – значение кривизны траектории в точке A ; τ – угол между касательной к траектории в точке A и осью x , и ψ = θ – τ [20].

В качестве фазовых переменных примем z ₁ – расстояние от целевой точки до целевой траектории CA , z ₂ = tg( ψ ), при этом управление формируется согласно результатам, представленным в работе А. В. Пестерева и Л. Б. Рапопорта [22]. Таким образом,

( ^ k ( s ) ° ( z )

u " Su [ ^( (1 - k (s) z1 )"(1 + z 2 )3/2 J, где z = (z1, z2)T, a функция сатуратор su, обусловленная ограничениями на ресурс управления, как и ранее, определена как

S u = { - u , u <- u , u , | u | <  u , u , u >- u I , где u – заданное ограничение, а линейная функция σ ( z ) задается в виде

о (z) = X2z1 + 2Xz2, X > 0.

В рассматриваемой постановке исходная задача траекторного управления в целом не разделяется для реального робота, его натурной и виртуальной моделей, за исключением лишь способов определения фазовых переменных z ₁ и z ₂.

Для виртуальной модели фазовые переменные могут быть определены следующими двумя способами:

• а)    на основе использования известных кинематических соотношений

и аналитических зависимостей для сплайнов и других траекторий, экспортированных с использованием API CAx-систем и их приложений6;

• б)    на основе непосредственного экспортирования значений переменных z ₁ и z ₂ из CAx-модели в процессе моделирования движения.

Вторая процедура возможна, если параметрические свойства модели должным образом сформированы, например так, как это показано на рисунке 4. Видеоролик наглядно демонстрирует эти свойства⁷. В этом случае в зависимости от положения робота изменяются z ₁ = || CA || и z ₂ = t ( ψ ) = tg( θ – τ ), но при этом сохраняются заданные параметрические взаимосвязи (принадлежности, касательности, перпендикулярности).

Проведенные нами численные эксперименты показали, что результаты, полученные способами «а» и «б» близки друг другу с высокой (не менее 1e-07) точностью. Способ «б» имеет особое значение в тех случаях, когда траекторию трудно задать аналитически.

Натурная реализация и моделирование

Для натурной модели платформы значения фазовых переменных определяются на основе анализа данных, поступающих от трех модулей очувствления роботизированной системы:

– модуль визуальной одометрии состоит из двух цифровых камер, определяющих смещение и поворот платформы в пространстве на основе данных с камер8 [25];

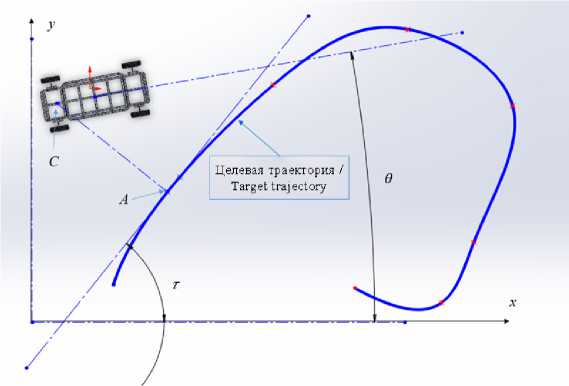
Р и с. 4. Параметрическая модель для траекторного управления по сплайну

F i g. 4. Results of numerical simulation to bring and to stabilize robot motion along spline path

– модуль инерциальной навигации состоит из гироскопа и акселерометра и позволяет определить линейные и угловые перемещения платформы в пространстве [26];

– модуль спутниковой навигации с приемником спутникового сигнала по типу GPS/GLONASS [27].

Программно-аппаратный модуль управления тестировался на натурной модели, собранной на платформе Arduino и fischertechnik [28–30]. Заметим при этом, что последующий перенос программного обеспечения с натурной модели на реальную платформу потребует лишь настроить интерфейс на конкретные физические сенсоры, обеспечивающие точное определение фазовых переменных.

На рисунке 5 показана натурная модель, обеспечивающая тестирование всех рассмотренных алгоритмов и включающая в себя основной привод движителей, рулевое управление (в варианте классической компоновки) и поворот видеокамеры. Видеоролик наглядно иллюстрирует работу натурной модели9. Траекторное управление рассчитывалось при этом сразу для всей траектории, то есть возможное проскальзывание, неровность поверхности движения и прочие возмущения не учитывались.

Программный модуль представляет собой многодокументное Windows-приложение архитектуры «документ-вид» (среда разработки MS VisualStudio C++/MFC/COM/vMicro(Arduino)/ APISolidWorks) и развивает опыт авторов в разработке приложений данного типа10 [31; 32]. В окне вида отображается масштабированная карта местности, полученная с геоинформационных систем или наземных станций управления и предназначенная для планирования траектории движения робота.

Р и с. 5. Натурная модель мобильного робота

F i g. 5. Physical model for mobile robot

Основная особенность программной реализации состоит в том, что управление как функция времени формируется и передается в качестве входных данных на виртуальные и физические устройства (моторы) в рамках одного программного модуля, сформированного одним проектом (projectsolution) MS VisualStudio C++.

Окно приложения показано на рисунке 6. Модальная диалоговая панель служит для постановки задачи, ввода исходных данных и компоновки шасси. Возможны два следующих режима работы программы:

• 1)    с использованием базовой CAx-системы в качестве COM-сервера и, соответственно, с использованием API этой системы (на рисунке 8 показан пример в варианте CAx SolidWorks );

• 2)    работа в автономном режиме.

В первом случае карта местности загружается в эскиз документа CAx, во втором случае – в окно вида приложения. Первый режим работы целесообразно использовать, если есть необходимость анализа проектного решения соответствующих статических, кинематических, динамических и прочих характеристик системы.

Траектория в обоих случаях формируется пользователем непосредственно в окне вида или документа (эскиза) с использованием стандартных средств графического редактирования.

Первый этап состоит в организации импорта-экспорта данных для CAx-модели робототехнической системы и тракторного управления. В качестве базовой CAx-среды используется SolidWorks, а решение задачи импорта-экспорта решается с использованием COM-интерфейсов и API SolidWorks.

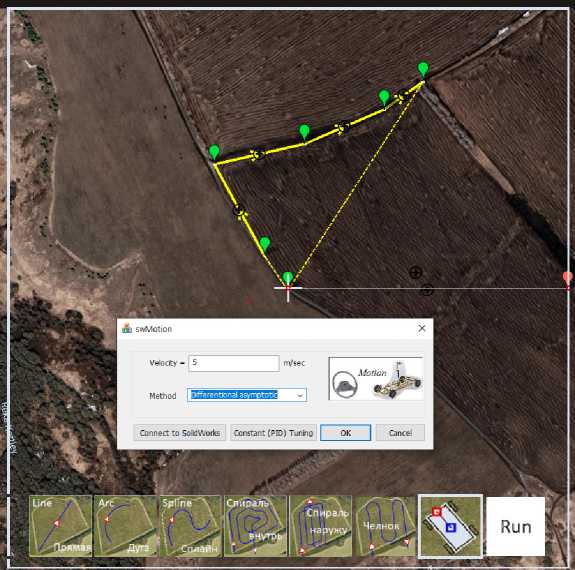
Р и с. 6. Окно приложения

F i g. 6. Application window

Наше приложение относится к типу Stand-Alone, которое подключается к текущему экземпляру COM-сервера sldworks.exe на локальном компьютере посредством использования smart-указателя CComPtr и вызова для него функции CoCreateInstance. Функция-обработчик кнопки Connect CAx реализует также определение указателя на текущий документ или открытие необходимого документа SolidWorks.

В контексте рассматриваемой задачи необходимо отметить два момента, которые требуют рассмотрения с точки зрения программной реализации: получение (импорт) данных из CAx-модели; определение (экспорт) данных для моделирования в CAx-среде.

На рисунке 7 показан фрагмент программного кода, реализующего доступ к фитчерам модели, в частности, к эскизу с именем Position и мотору в дереве моделирования с именем Drive11 (в наших обозначениях Driveij i = 1, j = 1), а также чтение (импорт) значения размера с именем Distance. В наших обозначениях этому параметру соответствует фазовая переменная z1 = ||CA|| (рис. 4).

Задача экспорта данных решается сразу в двух направлениях, то есть полученные управления экспортируются в качестве входных данных как для виртуальной модели (виртуальных шаговых моторов), так и аналогичных физических устройств натурной модели.

На рисунке 8 показан фрагмент кода для экспорта данных моделирования, причем на рисунке 8a в направлении CAx SolidWorks, в частности, doc->IFirstFeature( while (pFeature) // Цикл по фитчерам

{ pFeature->get_Name( if (Name == _T("Position"))// получение имени фитчера и проверка требу-

емого {

имени

VARIANT_BOOL ret;

pEnumDispDim = NULL;

pFeature->Select(TRUE, &ret); //выбор текущего фитчера pFeatureControl = pFeature;

pFeatureControl->EnumDisplayDimensions(&pEnumDispDim); // получение указателя на размеры модели

if {

(pEnumDispDim)

pEnumDispDim->Next(1, &pDisplayDimension, &NumberDim); while (NumberDim)// цикл по размерам

{

if //

pDisplayDimension->IGetDimension(&pDim);

pDim->get_FullName(&Name);// получение имени размера pDim->get_Value(&Value); // получение значения размера с именем Distance

(Name == _T("Distance@Position"))

Distance = Value;

}

} // if

{

}

}

определение других требуемых параметров аналогично pDisplayDimension = pDisplayDimensionNext;

pEnumDispDim->Next(1, &pDisplayDimension, &NumberDim);

(Name

== CComBSTR(_T("Drive11")))// Если имя фитчера Drive11

}

pSubFeature->GetDefinition(&pDisp);

pDisp->QueryInterface(&pFeatureMotorData_u1);

Р и с. 7. Доступ к фитчерам модели

F i g. 7. Accessing to model features

// Определение входных данных для мотора как фитчера моделирования doc->EditSketch(); // Режим редактирования эскиза

VARIANT spData_u1; // Определение объекта типа Variant

SafeDoubleArray my_u1(spData_u1); // Определение безопасного массива double CurrentTime = 0.0;

for (int k = 0; k <= NumberTimeLineStep; k++) //

Цикл по времени

{ my_u1[k] = CurrentTime;

my_u1[k + NumberTimeLineStep + 1] = u1[k];

// Упаковка сформированных данных в массив

CurrentTime += TimeLineStep; // Шаг по времени

} pFeatureMotorData_u1->put_SplineData(spData_u1);

a)

GStepper< STEPPER2WIRE> stepper(steps, step, dir); // steps – количество шагов на один оборот вала, step, dir ‒ порт ввода-вывода общего назначения k=0;

void loop()

if (millis() - tmr2 > time_step)

{

tmr2 = millis();

static float val;

if (millis() = = my_u1[k]*1000)

{ val = u1[k]; k++;

stepper.setTarget(val); // ставим новую позицию для шагового мотора

}

}

};

b)

Р и с. 8. Экспорт управления в виртуальную модель и натурный объект

F i g. 8. Export of control to virtual model and to physical object

Technologies and means of agricultural mechanization                                         621

выполняется определение исходных данных для Drive11, то есть массив my_u1 содержит данные табулирова- ния функции tg(«1) =

uL uH —

. На рисун-

ке 8b та же задача решается для определения входных данных для физических устройств, управляемых контроллером семейства Arduino с использованием библиотеки управления шаговыми двигателями Stepper11.

Обсуждение и заключение

Разработан программно-аппаратный модуль траекторного управления интегрированной виртуальной и натурной моделью для мобильной роботизированной платформы. Выполнено тестирование алгоритмов, обеспечивающих экспоненциальную устойчивость управления для траекторий различного вида: отрезка прямой, дуги окружности, сплайна (Безье).

При этом виртуальная CAD/CAE-модель позволяет исследовать состо- яние и поведение конструкции как многотельного объекта в различных режимах ее эксплуатации в терминах механики деформируемого твердого тела.

Программно-аппаратные модули имеют открытый интерфейс и могут быть легко интегрированы в кибер-физические системы управления и автономизации техники более общего вида. При этом полученное управление как функция времени передается в виде управляющего сигнала как на виртуальные, так и на физические устройства. Программно-аппаратное обеспечение и виртуальные модели платформы предусматривают различные варианты компоновки, могут быть адаптированы к требованиям потребителя и предоставлены ему как сервис.

В части использованных алгоритмов управления и их программной реализации отсутствуют существенные различия между управлением реальным объектом, его виртуальной и натурными моделями. В этом смысле проект готов к практической реализации и внедрению в практику точного земледелия.

В качестве перспектив проекта следует указать следующие:

• 1.    Аппаратная реализация управления самоходными базами «Пегас-Агро». Эта задача предусматривает совместную с «Пегас-Агро» разработку мехатронных систем, максимально адаптированных к конструктивным особенностям самоходных баз и технологической среде предприятия.

• 2.    Интеграция мобильной роботизированной платформы в мультиаген-тную систему в качестве агента.

При этом для решения каждой из этих двух задач программное обеспечение системы управления каких-либо существенных изменений не потребует.

Поступила 28.06.2021; одобрена после рецензирования 10.08.2021; принята к публикации 17.09.2021

Об авторах:

Все авторы прочитали и одобрили окончательный вариант рукописи.

Technologies and means of agricultural mechanization 625

Submitted 28.06.2021; approved after reviewing 10.08.2021; accepted for publication 17.09.2021

All authors have read and approved the final manuscript.