Интегрированная модель нефтяного месторождения, учитывающая эффект автоматического гидроразрыва пласта

Организация производства на нефтяном промысле является нетривиальной задачей, которая обусловлена спецификой разработки месторождений жидких углеводородов. Данный процесс представляет собой сложную структуру взаимосвязанных между собой во времени и пространстве подпроцессов, которые могут идти как последовательно, так и параллельно: проведение геологоразведочных работ на территории лицензионного участка, проектирование системы разработки месторождения, создание необходимой поверхностной инфраструктуры, в том числе бурение эксплуатационного фонда скважин, а также последующие управление и контроль за процессом разработки, ликвидация скважин. Кроме того, задача осложняется высокой степенью неопределенности параметров пласта и флюидов, точность оценки которых ограничена тем, что большинство применяющихся методов измерений дают лишь косвенную информацию с высокой долей погрешности, а количество таких исследований часто бывает недостаточным. Исходя из вышесказанного применение системного подхода является необходимым условием повышения качества планирования и реализации процесса добычи нефти и газа.

На текущий момент ключевым инструментом позволяющим наиболее полно описывать технологические процессы разработки на всех стадиях жизненного цикла месторождения является интегрированная модель (ИМ) производственной системы нефтегазового предприятия. Она представляет собой модель, состоящую из связанных между собою моделей-компонентов с едиными начальными и граничными условиями: модель пласта, модель скважины и модель поверхностной сети, которая включает в себя систему сбора и транспорта добываемой продукции, а также систему поддержания пластового давления (ППД), которая в большинстве случаев используется для реализации вторичного метода увеличения нефтеотдачи – заводнения. Заводнение – это «закачка в нефтяную залежь воды через специальные нагнетательные скважины для поддержания пластового давления, повышения извлечения нефти и темпа отбора нефти в соответствии с проектными документами» [1].

Одной из основных проблем, встречающихся при организации закачки воды в низкопроницаемый коллектор, является образование трещин автоматического гидроразрыва пласта (АГРП), способных расти как по вертикали, так и по горизонтали (см. рис. 1). Данное явление возникает при превышении забойным давлением давления разрыва породы и может приводить как положительным, так и негативным последствиям, снижающим качество процесса ППД и добываемой продукции. Необходимо отметить, что трещина АГРП отличается от, намеренно создаваемой для интенсификации притока к скважине, трещины ГРП наличием в последней расклинивающего агента (проппанта), предотвращающего ее смыкание. На текущий момент технология гидроразрыва пласта (ГРП) доминирует в качестве основного типа заканчивания добывающих и нагнетательных скважин.

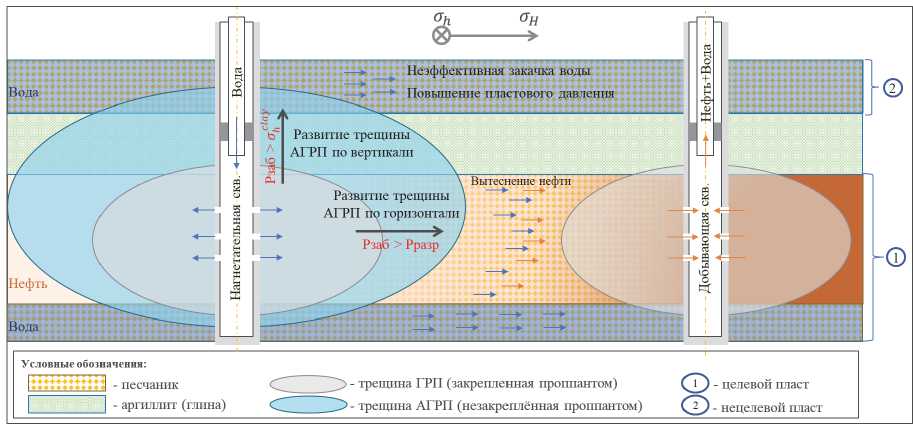
Рис. 1 – Схематическое изображение трещины АГРП

К негативным последствиям, вызванным явлением АГРП, относятся потери добычи нефти, обусловленные преждевременным обводнением добывающих скважин, расположенных по направлению максимального горизонтального напряжения, вдоль которого обычно распространяются техногенные трещины. Другим примером является нецелевая закачка агента вытеснения по трещинам АГРП в выше- и/или нижележащие горизонты, приводящая к аномально высоким пластовым давлениям (АВПД) в нехарактерных для этого интервалах, снижению эффективности закачки и как следствие увеличению непроизводительной доли операционных затрат (см. рис. 1). Увеличение капитальных вложений может происходить за счет потерь времени, вызванных необходимостью утяжеления бурового раствора из-за вскрытия пластов с АВПД в несвойственных для этого зонах. Игнорирование трещин АГРП при гидродинамическом моделировании может привести к ошибочной оценке остаточных извлекаемых запасов (ОИЗ), в результате чего новые скважины часто бурятся в уже обводнённые зоны, что снижает показатели их эффективности.

К положительному эффекту, выраженному в повышении коэффициента охвата вытеснением нефти водой, может привести образование магистральной трещины АГРП в ряду нагнетательных скважин, расположенному вдоль направления действия максимального горизонтального напряжения, а также, например, контроль длины трещины АГРП, рост которой не приводит к преждевременному обводнению соседней добывающей скважины.

Моделированием самопроизвольно развивающихся техногенных трещин ученые начали заниматься с конца XX века. Одной из первых работ по созданию численной модели была статья J. Hagoort [2]. В ней представлена связка однофазной модели пласта традиционного симулятора и аналитической модели трещины типа KGD [3]. В дальнейшем данная модель была усовершенствована в работе [4] в предположении плоских деформаций с учетом дополнительных напряжений, возникающих из-за изменения порового давления в пласте в течение длительной закачки жидкости.

В последнее время набирают популярность полностью связанные численные модели развития трещин АГРП на основе уравнений пороупругости [5] для описания взаимного влияния изменения порового давления на напряженно-деформированное состояние (НДС) породы [6, 7, 8]. В работах [6,9,10] приведены модели пласта для многофазной фильтрации, влияния которой рассматривалось еще в [11]. Отметим, что учёт данного эффекта позволяет прогнозировать преждевременный прорыв воды, что является важным для оптимизации процесса заводнения.

Модели, представленные в приведенных научных публикациях, не включают в себя уравнения, описывающие поведение объектов поверхностной инфраструктуры. Анализ литературных источников показал, что лишь в исследовании [12] зафиксировано применение интегрированной модели, учитывающей динамику развития трещин АГРП, для построения диаграмм Холла. При этом авторы не приводят математической постановки задачи, что не позволяет выявить возможные ограничения и оценить адекватность разработанной модели.

Целью данной работы является создание интегрированной модели нефтяного месторождения, учитывающей эффект автоматического гидравлического разрыва пласта, которая позволит повысить качество процессов проектирования и управления производственной системой месторождения углеводородов.

1.    МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

На текущий момент большинство реализаций интегрированных моделей сделаны на основе метода узлового анализа [13-15]. В основе подхода лежит концепция разбиения сложной системы с помощью так называемых узлов на взаимосвязанные, но относительно независимые компоненты, каждый из которых описывается собственным набором уравнений и параметров. Особенностью метода является то, что выходные параметры одного элемента автоматически становятся входными параметрами для следующего, что создает замкнутую расчетную схему.

Наиболее частым примером метода узлового анализа, приводимым в литературе, является поиск точки пересечения кривой притока из пласта (Inflow Performance Relationship) и кривой вертикального лифта скважины (Vertical Lift Performance) для определения дебита жидкости добывающей (см. рис. 2a) и приемистости нагнетательной скважины (см. рис. 2б) при заданных условиях.

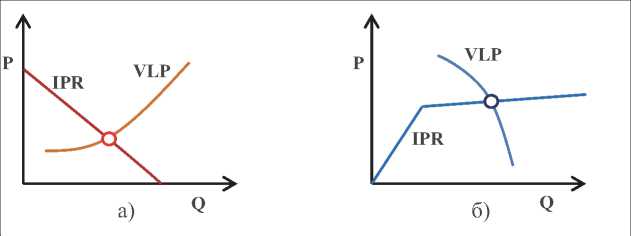
Рис. 2 – Схематическое изображение пересечения IPR и VLP кривых для добывающей (а) и нагнетательной скважины с АГРП (б)

Преимущество такого подхода заключается в возможности детального анализа каждого элемента системы при сохранении целостного представления о работе всего месторождения, что особенно важно при выявлении «узких мест» в системе добычи или оптимизации режимов работы поверхностного оборудования.

Второй подход реализации интегрированной модели месторождения подразумевает решение единой системы уравнений полностью неявным методом [16]. Преимущество данного способа по сравнению с методом узлового анализа состоит в сокращении времени расчета модели примерно в 10 раз [17].

Для реализации ИМ выбран второй подход, так как именно скорость расчета является критически важным моментом при решении и без того сложной и требовательной к вычислительной мощности задачи роста трещины АГРП. Разработанная ИМ включает в себя модель пласта и модель поверхностной сети.

Модель пласта представляет собой двухфазную (нефть и вода) гидрогеомеханическую двумерную модель, позволяющую моделировать развитие трещин АГРП (рост, смыкание). Отличительной особенностью данной модели от обычной гидродинамической является учет пороупругости, которая оказывает существенное влияние на динамику и момент инициации трещины АГРП. Пороупругая составляющая представляет собой зависимость деформации породы пласта от давления и потока флюидов в поровом пространстве породы пласта и наоборот.

В качестве расчетной области Ω рассматривается прямоугольный участок месторождения (см. рис. 3). Добывающие и нагнетательные скважины вскрывают один пласт высотой h(x) , где x = (x, y) – радиус-вектор. Коллектор представлен песчаником, который, в свою очередь, является пороупругой средой и содержит нефть и воду c динамическими вязкостями µ _o и µ _w соответственно. Горная порода характеризуется своей пористостью ϕ ( x ) , проницаемостью k( x ) , водонасыщенностью S _w , поровым давлением p , перемещением твердой фазы u (t , x ) , модулем Юнга E , коэффициентом Пуассона ν и коэффициентом Био α . Оси Ox и Oy и параллельны региональным максимальным σ _H и минимальным σ _h горизонтальным напряжениям соответственно.

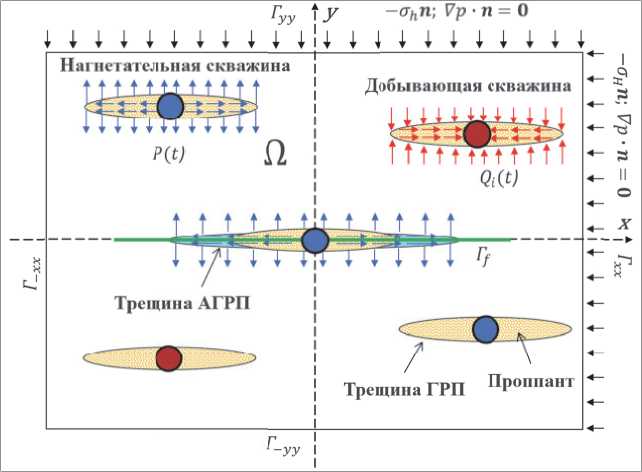
Рис. 3 - Постановка задачи роста трещины АГРП с учетом двухфазной фильтрации в пласте

Модель поверхностной сети представляет собой одномерную двухфазную гидравлическую модель, позволяющую описывать параметры течения смеси в системе наземных и подземных сооружений месторождения на основании входных данных, характеризующих состояние системы сбора и транспорта (ССиТ) добываемой продукции, системы ППД и скважины: длины, диаметры, абсолютные отметки частей трубопроводов, диаметры штуцеров, характеристики кустовых и дожимных насосных станций, связи объектов, инклинометрия, конструкция скважины (диаметры, глубины спусков обсадных колонн, насосно-компрессорных труб, пакеров и т.д.), характеристики погружного оборудования (электроприводной центробежный насос (ЭЦН)) и т.д. Скважина рассматривается как продолжение поверхностной сети, так как уравнения, описывающие течение многофазной смеси в трубопроводе и скважине, идентичны.

Схематичное представление примера производственной системы изображено на рисунке 4. Система сбора и транспорта углеводородов начинается с отверстий перфорации или порта ГРП скважины, она может состоять из самой добывающей скважины, имеющей погружное оборудование (например, электроцентробежный насос), штуцеров, автоматизированной групповой замерной установки (АГЗУ), дожимной насосной станции (ДНС), трубопроводов, связывающих перечисленные объекты сети. Система ППД может включать кустовую насосную станцию (КНС), блок гребенок (БГ), штуцер, нагнетательную скважину с перфорациями или портами ГРП, трубопроводы.

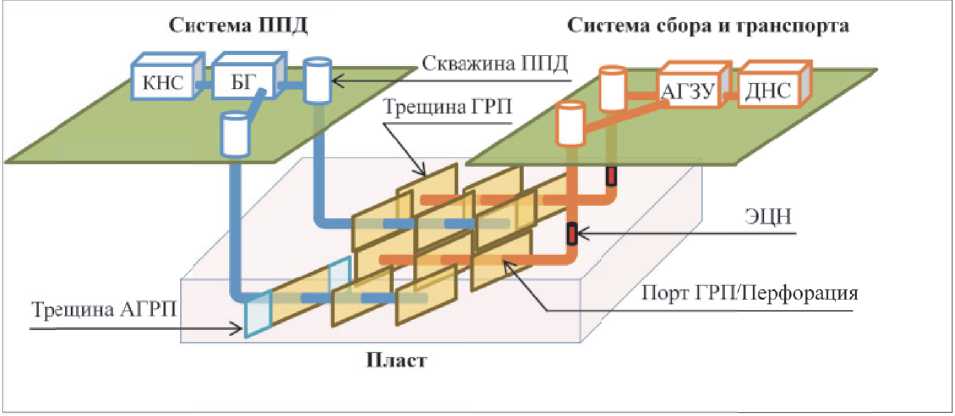
Рис. 4 - Схематичное представление производственной системы нефтяного месторождения

Далее приведем обобщенную единую систему основных уравнений для интегрированной модели «пласт - поверхностная сеть»:

' V ■ и —V ■ {Xdiv(u)I + G(Vu + Vu ^T ) — ар!) — О, ^d-^p + v- (—Pi^Vp'j — O,

c{n)\rf —

^гcont (w⁾)n,

V

^^wt^ + V x ■ (p^h) + v_u(x, t⁾h — Zj m^S^x — x j ), S w + S o — 1, dCS _iPi A⁾ д^ ; р ; ^т/р)

_dt⁺--- at---- ^{— — Z} j ^m ij 8⁽l ^— l j ),

Ар — F (p,S_w> ^m , params^

vE „ где с - тензор полных напряжений, X — ^i^vj(1"2V), G — 2(i+v — параметры Ламе, i — o,w - индекс,

указывающий на фильтрующуюся фазу (вода или нефть соответственно), j

–

индекс,

указывающий на номер порта ГРП перфорации, p_t - плотность фазы i , у — у₀^1 + с ^ {р — p ref )) -пористость горной породы, у₀ - начальная пористость пласта, c_v - сжимаемость пор, р ref -опорное давление, k_ri - относительная фазовая проницаемость флюида i , р у - давление в трещине, которое равно давлению в примыкающей горной породе на ее стенках р , a_cont — max(y_p(w f — w),0) - контактное напряжение, w — [u]\_r f - раскрытие трещины АГРП, q fi —

'wk p k p _r i I maxQ(w—w

Л ;

12м ;

^f) ’^ ^xP f — поток флюида по трещине, k_p , k_pri - абсолютная и относительная

фазовая проницаемость проппантной пачки соответственно, м у - ширина трещины ГРП, v_u — [Pi^^Vp'W - утечки жидкости i из трещины в пласт, 8 - одномерная дельта-функция Дирака, m^ - массовый расход фазы i , поступающий или добываемый из j порта ГРП/перфорации скважины, р - - плотность фильтрующейся фазы i при стандартных условиях, А - площадь поперечного сечения объекта поверхностной сети, т - массовый расход смеси, I - длина объекта поверхностной сети, F - функция, определяющая поведение объекта поверхностной сети, params - набор параметров, описывающих объект поверхностной сети (например, диаметр, длина и т.д.).

Первые два уравнения системы представляют собой уравнения пороупругости Био, а именно уравнение равновесия и уравнение переноса для каждой рассматриваемой фазы в горной породе. Следующие два уравнения задаются на границе Г у , определяющей потенциальную область распространения трещины АГРП и область существования закрепленной трещины ГРП. Первое из них - это баланс сил, действующих перпендикулярно границе Г у . Он представлен воздействием давления р на стенку трещины и контактными напряжениями a_cont [8], которые предотвращают взаимное проникновение берегов трещины АГРП и учитывают преднапряженное состояние, вызванное наличием закрепленной трещины ГРП шириной W f [18]. Критерием образования трещины АГРП (трещины отрыва, I мода деформации) является превышение давлением р у на закрепенной трещине ГРП расчетного значения давления инициации, полученного из первого соотношения системы. Следующее уравнение - описывает течение нефти и воды по трещинам ГРП и АГРП. Пятое соотношение представлено суммой насыщенностей двух фаз, которая равняется единице. Остальные уравнения описывают течение жидкости по поверхностной сети и скважине, а их вид зависит от конкретного реализованного объекта инфраструктуры: труба, штуцер, ЭЦН, КНС (источник), ДНС (сток), узел, перфорация скважины/порт ГРП. Шестое уравнение представляет собой закон сохранения массы для текущей жидкости i . Необходимо отметить, что первое слагаемое отвечает за нестационарность процесса течения флюида по трубам (линейный объект) и обращается в нуль для точечных объектов (например, ЭЦН, штуцер, узел). Седьмое соотношение написано в общем виде и отвечает за перепад давления на элементе поверхностной сети. Например, для узла перепад давления будет вовсе отсутствовать, а на штуцере равен ₂?™ _A) _Z , где CD - коэффициент, учитывающий несовершенства и необратимые потери, такие как трение и теплопередача, А - площадь поперечного сечения отверстия штуцера.

В рамках рассматриваемой модели были приняты следующие допущения:

• •    Давление в пласте в процессе разработки не снижается ниже давления насыщения нефти газом, поэтому фильтрующиеся жидкости можно считать слабосжимаемыми средами.

• •    Пренебрегаем влиянием капиллярных сил и силой тяжести.

• •    Процесс течения флюида является изотермическим.

• •    В модели поверхностной сети смесь будем считать однородной, поэтому скорости нефти и

• воды совпадают.

• •    В задаче роста трещины АГРП силами сцепления породы в виду их незначительного влияния можно пренебречь.

• •    Трещины АГРП растут прямолинейно вдоль максимального горизонтального напряжения. Плотности фильтрующихся жидкостей определяется следующим образом:

nst р№ = ыу                             (2)

B-ef

В-Р) — l+ci(p-p^efy                                                (3)

где pf^t,B _i - плотность фильтрующейся фазы i при стандартных условиях и изотермический коэффициент объемного расширения соответственно, c _i - сжимаемость флюида i , которая является постоянной величиной, В™ ? - объемный коэффициент фазы i при некотором опорном (референсном) давлении р^гер .

Плотность и вязкость смеси «вода-нефть» в поверхностной сети вычисляются по формулам:

Р P w ^S w + P o ^S o , ^р P w ^S W ^Т P o ^S O ‘

В модели пласта на внешних границах рассматриваемой области О задаются сжимающие напряжения и условие непротекания (см. рис. 3):

Г хх , ^р -хх -^ — ~^ н п, Г _уу ,Г -уу. а(п) — -a _h n, где Vi - скорость фильтрации фазы i .

Граничные условия на источнике (КНС) задаются

v _i -п = О, v _i - п — О,

в

виде насыщенности S _w = S _w (t) , давления

р — p(t) или массового расхода т = m(t) при соответствующем контроле. На стоке (ДНС) задаются аналогичные условия, однако водонасыщенность будет определяться входящим потоком.

Систему также необходимо дополнить начальными условиями.

Для модели пласта:

^\ t=0 ^{— a} 0 ^{, u} \ t=0 ^{— U} 0 ^{, p} \ t=0 ^{— p} 0 ^{, S} w \ t=0 ^{— S} WW ^, Ф ^{— ф} 0 - Для модели поверхностной сети:

^S w \ t=0 — ^S w , q\ t=0 ^{— 0} - Начальное давление p ₀ при t — 0 соответствует гидростатическому давлению в трубе.

2.    ЧИСЛЕННЫЙ АЛГОРИТМ

Численная реализация модели основана на методе конечных объемов, который обеспечивает консервативность дискретной схемы. Для линеаризации нелинейных уравнений применяется итерационный метод Ньютона - Рафсона.

J ^k X ^k+l —-R ^k +J ^k X ^k , (11) где к - номер итерации, J ^k - матрица Якоби, R ^k - невязка системы на предыдущей итерации к , X ^k+l - вектор неизвестных на давление, насыщенность, перемещения твердой фазы, массовый расход жидкости.

Дискретизация пласта выполняется с использованием квадратной неструктурированной сетки. Давление, водонасыщенность, перемещения определены в центре ячейки (см. рис. 5а).

Линейные объекты О поверхностной сети разобьем на N j контрольных объемов, как показано на рисунке 5б. Неизвестные системы уравнений давление р[ и водонасыщенность S _w,_i определены в центре отрезков, а массовый расход смеси m _i - на концах отрезков. За р ₀ , S _w0 и p _Nj+l , S _wN . _+l обозначим давление и водонасыщенность на концах объектов. Перфорация/порт ГРП, источник/сток не имеют длины, потому все неизвестные находятся в одной точке. Штуцер, насос представлены одной ячейкой, все искомые переменные заданы на концах отрезка.

Реализация поставленной задачи выполнена на языке C++ с помощью платформы INMOST с использованием автоматического дифференцирования [19].

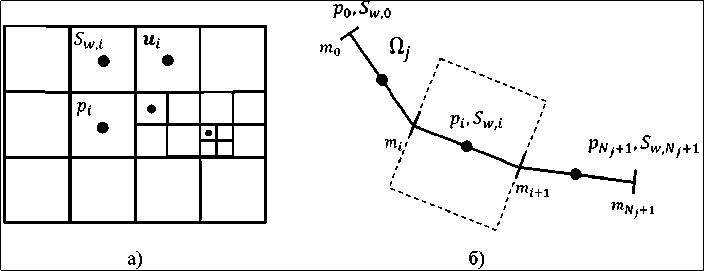
Рис. 5 – Дискретизация расчетной области а) пласта и б) линейного объекта поверхностной сети

3.    ВЕРИФИКАЦИЯ МОДЕЛИ

Для проверки корректности реализации модели была проведена ее верификация с помощью ПО «ТНавигатор» [16]. В качестве тестовой симуляции выбран комплексный сценарий, включающий все доступные объекты поверхностной сети. Далее приведем его подробное описание.

На рисунке 6 представлена расчетная схема решаемой задачи, на которой изображены расположение скважин относительно друг друга и рассматриваемого участка пласта, а также конфигурация объектов наземной инфраструктуры, состоящей из трубопроводов, источника, стока, штуцеров и узла.

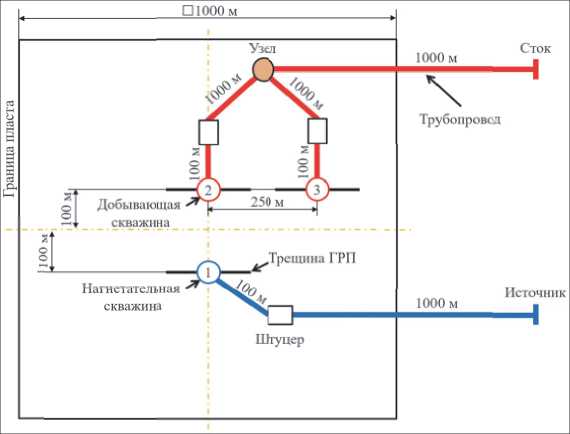
Рис. 6 – Схема расположения скважин для задачи верификации

Система сбора и транспорта добываемой продукции состоит из двух добывающих скважин с ГРП, соединенных между собой с помощью узла трубопроводов, штуцеров, позволяющих регулировать режимы работы каждой скважины отдельно, пяти трубопроводов, по которым происходит транспортировка жидкости к стоку. Система ППД состоит из нагнетательной скважины с ГРП, штуцера, двух трубопроводов и источника воды. Расчетная область имеет квадратную форму и представляет собой продуктивный пласт, насыщенный нефтью и водой. Все скважины являются вертикальными, их устья расположены на нулевой отметке относительно уровня моря. Верхние дыры перфораций находятся на глубине 2000 метров. Конструкции скважин идентичны за исключением наличия ЭЦН в добывающих.

На источнике и стоке на протяжении всего расчета заданы постоянные давления 150 и 100 бар соответственно. Диаметр штуцера на добывающих скважинах также не меняется и составляет 10 мм. Диаметр штуцера на нагнетательной скважине 01.08.2025 года уменьшается с 18 мм до 5 мм. Частота насоса на скважине №2 неизменна на протяжении всего периода расчета и равна 70 Гц. Частота насоса на скважине №3 меняется с 40 Гц до 42 Гц 01.06.2025 года.

На рисунке 7 приведены рассчитанные показатели работы скважин. Пунктирной линией изображены кривые, полученные в ПО «ТНавигатор», сплошной линией – с помощью разработанной интегрированной модели.

На нагнетательной скважине наблюдается постепенный рост приемистости при неизменном забойном давлении, который сменяется резким падением обеих кривых вследствие уменьшения диаметра штуцера: повышение местного сопротивления приводит к снижению величины репрессии на пласт, что, в свою очередь, сказывается на значениях расхода закачиваемой воды. В то же самое время данное изменение в виду относительно высокой проницаемости коллектора отражается на режимах работы обеих добывающих скважин: сокращение объемов закачки снижает эффективность поддержания пластового давления, что влечет за собой уменьшение дебитов жидкости соседних скважин. Резкий рост объемов добываемой продукции и одновременное снижение забойного давления 01.06.2025 года являются следствием увеличения частоты насоса на скважине №3.

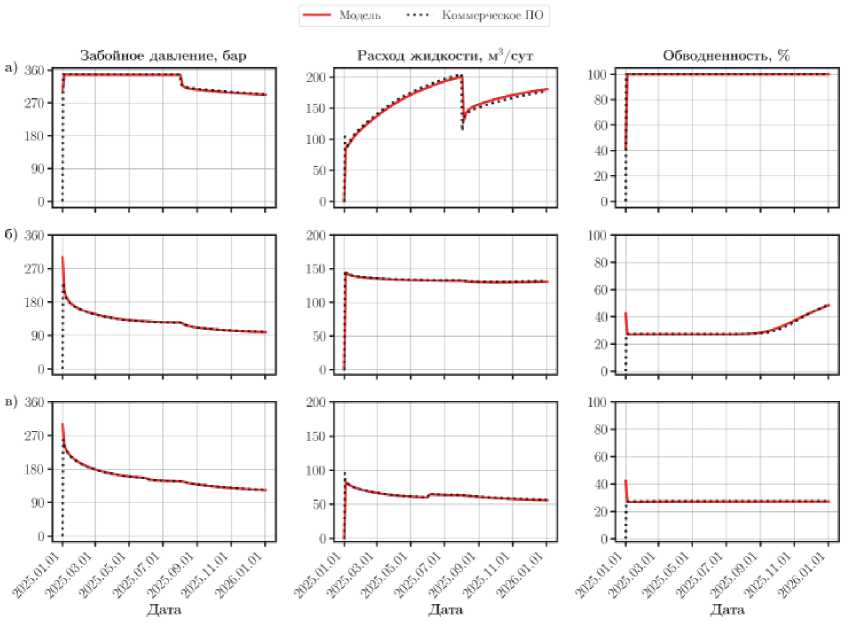
Рис. 7 – Показатели работы скважин а) №1, б) №2, в) №3 (верификация)

Таким образом, наблюдается хорошее совпадение результатов расчета с значениями эталонных кривых не только на качественном, но и на количественном уровне, что подтверждает успешную верификацию разработанной модели.

4.    РАСЧЕТЫ

Гидродинамические расчеты выполняются для задач проектирования системы разработки месторождения углеводородов [20] и оптимизации режимов работы действующего фонда скважин [21]. Очевидно, что игнорирование явления АГРП вследствие его существенного влияния на процесс поддержания пластового давления при заводнении может привести к принятию несовершенных или неправильных решений, которые в свою очередь могут привести к негативным последствиям, включая потерю добычи нефти.

Учет явления АГРП повышает адекватность используемых в нефтегазовой отрасли физико-математических моделей. Наглядный пример сопоставления модельных расчетов с учетом и без учета рассматриваемого явления представлен в работе [22]. В статье было проведено количественное сравнение модели роста трещины АГРП с традиционной моделью интерпретации гидродинамических исследований, используемой в ПО «Saphir», посредством фактических данных работы скважины. Анализ результатов показал, что показатели адекватности (MAE, RMSE, MAPE, WAPE) первой модели более чем в 2 раза выше по сравнению со значениями второй модели.

Далее для демонстрации возможностей и преимуществ созданной интегрированной модели рассмотрим два синтетических расчета.

Для первой симуляции за основу возьмем расчетную схему задачи верификации, сделав инверсию типов скважин и увеличив область (см. рис. 8). Зададим в качестве граничного условия контроль по расходу на источнике и в середине расчетного года увеличим диаметр штуцера на скважине №3 с 2мм до 10мм, а на скважине №2 оставим значение равное 2 мм.

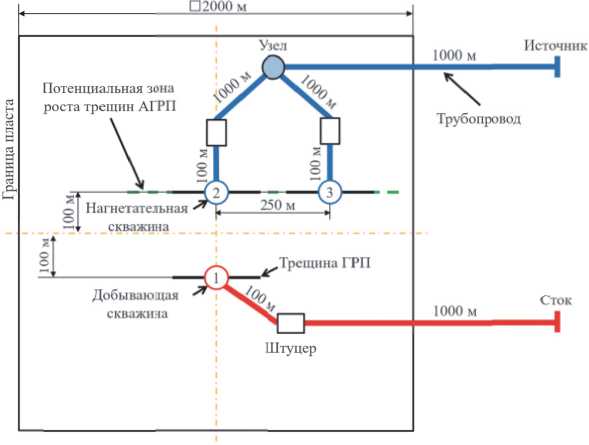
Рис. 8 – Схема расположения скважин (расчет №1)

На рисунке 9 представлены результаты первого синтетического расчета. Анализируя показатели работы скважин до момента смены режима работы скважины №3, можно сделать вывод о взаимовлиянии добывающей и нагнетательной скважин. Данное утверждение подтверждается тем, что на скважине №1 с течением времени происходит рост забойного давления с 17.5 до 18.7 МПа, при этом на скважине №2 значения забойного давления ниже по сравнению со скважиной №3, что указывает на более высокий коэффициент приемистости левой нагнетательной скважины, увеличение которого связано с наблюдаемой интерференцией скважин. В момент увеличения штуцера на скважине №3 забойное давление начинает превышать давление разрыва, что приводит к росту трещины АГРП. Образование и дальнейшее распространение трещины АГРП влечет за собой резкое увеличение коэффициента приемистости, которое связано с увеличением площади фильтрации флюида. Данный эффект приводит к перераспределению потоков в узле, соединяющем трубопроводы нагнетательных скважин. На скважине №2 резко падает забойное давление и расход, вследствие чего уменьшается влияние закачки воды на добывающую скважину.

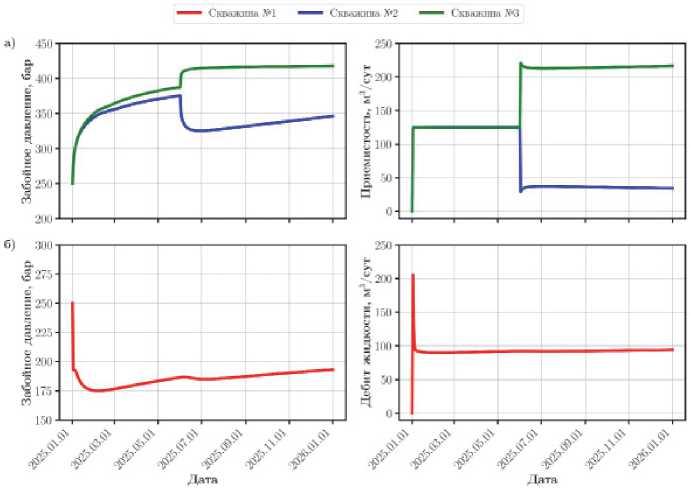
Рис. 9 – Показатели работы скважин а) №2 и №3, б) №1 (расчет №1)

Таким образом, по причине роста трещины АГРП произошло существенное перераспределение потоков воды в поверхностной сети, даже несмотря на то, что скважина №2 изначально имела коэффициент приемистости выше, чем у соседней скважины. Данный эффект невозможно промоделировать с помощью одной лишь модели пласта.

Во второй симуляции три скважины ППД находятся в одном ряду, расположенном вдоль потенциального роста трещин АГРП (см. рис. 10). Все скважины изначально работают на штуцере 2 мм, затем 01.06.2025 г. крайние скважины разжимают до 8 мм. На источнике задан контроль по давлению (210 бар).

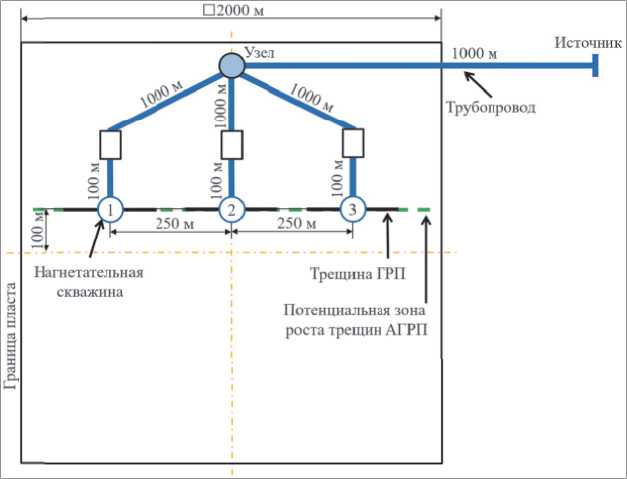
Рис. 10 – Схема расположения скважин (расчет №2)

На рисунке 11 приведены показатели работы трех нагнетательных скважин. До момента увеличения диаметров штуцеров скважины работали примерно с одними значениями забойного давления и объемного расхода за исключением последнего месяца. Видно, что кривая давления скважины №2 (синяя линия) с 05.2025 по 06.2026 находится немного выше остальных, это связано с влиянием соседних скважин посредством продуктивного пласта, куда ведется закачка флюида. В июне 2025 года происходит увеличение режимов работы на крайних скважинах при неизменном режиме работы центральной. Забойное давление на скважинах №1 и №3 достигает давления разрыва, что приводит к образованию трещин АГРП, которые практически сразу срастаются между собой в так называемую магистральную трещину АГРП, объединяющую все три скважины друг с другом высо-копроводящим каналом на уровне пласта. В момент роста трещин АГРП на крайних скважинах происходит увеличение объемного расхода воды до ~175 м3, в то время как на скважине №2 происходит уменьшение приемистости. Данный эффект «задавливания» центральной скважины, часто наблюдаемый на нефтяных месторождениях с продольной системой разработки, возникает вследствие образования магистральной трещины АГРП и не может быть корректно смоделирован без учета поверхностной инфраструктуры.

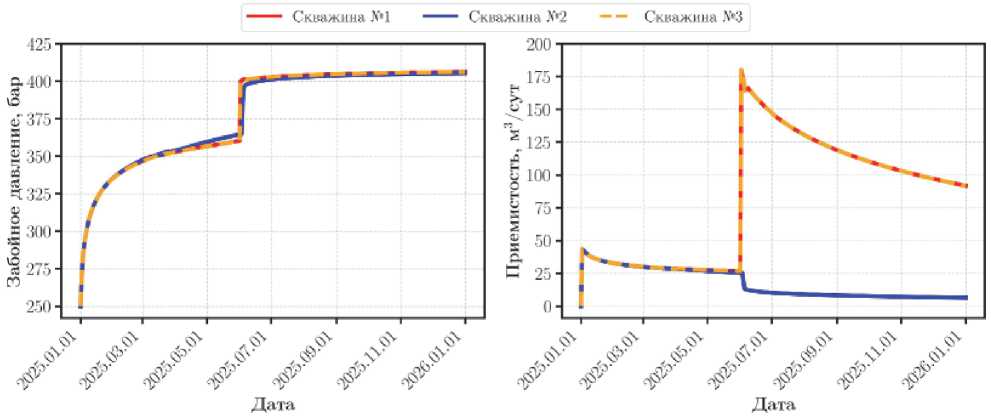
Рис. 11 – Показатели работы скважин (расчет №2)

Таким образом, все вышеперечисленное обуславливают необходимость учета роста трещин АГРП в моделях, применяемых для планирования и управления добычей нефти и газа, задачи которых наиболее полно можно решить с помощью интегрированной модели.

ЗАКЛЮЧЕНИЕ

В работе описана разработанная интегрированная модель нефтяного месторождения, которая отличается от существующих моделей пласта учетом объектов поверхностной сети и преднапря-женного состояния, вызванного трещиной ГРП, а от созданных ранее интегрированных моделей – учетом явления АГРП. Реализация выполнена с помощью неявной схемы интеграции подмоделей, которая обеспечивает ускорение расчетов в ~10 раз по сравнению с моделями, основанными на методе узлового анализа. Верификация модели выполнялась с помощью ПО «ТНавигатор». Результаты сравнения показали хорошее совпадение всех показателей работы моделируемых скважин.

Преимущества модели заключаются в моделировании производственной системы предприятия с учетом роста трещин АГРП, которые могут оказывать как положительное, так и отрицательное влияние на показатели качества разработки месторождений углеводородов. Возможности разработанной модели были продемонстрированы с помощью двух синтетических расчетов, результаты которых показали необходимость учета эффекта АГРП при проектировании и управлении системой заводнения нефтяного месторождения.

Внедрение интегрированной модели, учитывающей явление АГРП, позволит оптимизировать организацию производственных процессов, уменьшить потери и повысить общую управляемость системы. Это соответствует принципам современного менеджмента качества, где ключевыми критериями являются стабильность процессов, минимизация отклонений и эффективное управление рисками. Таким образом, предлагаемая модель не только способна решить технические задачи нефтедобычи, но и будет содействовать совершенствованию системы управления качеством на нефтегазовом предприятии благодаря учету влияния трещин АГРП на процесс добычи нефти и газа, обеспечивая сбалансированные решения по режимам работы скважин исходя из ограничений инфраструктуры.