Интегрированный электромеханический комплекс

Структура интегрированного электромеханического комплекса (ИЭМК), представляющего собой многофункциональный объект исследований (МФО), основывается на концепции интегрированных комплексов сетевых автоматизированных лабораторий [1] (рис. 1).

Рис. 1. Структура интегрированного электромеханического комплекса

ИЭМК объединяет совокупность технических, математических, программных и методических средств, обеспечивающих научные исследования объектов машиностроения. Базовые компоненты ИЭМК – модели: математические (ММ) и физические. Физические модели включают в себя установки с машинами постоянного тока (МПТ), асинхронными (АМ) и синхронными (СМ) машинами. Математические модели электромеханических систем строятся на базе теории обобщённого электромеханического преобразователя (ЭМП) в двухфазных системах координат: u, v, α, β, d, q, x, y. Математическое моделирование и экспериментальные исследования вентильных (ВП) и электромеханических преобразователей и систем на их основе – управляемых вентильноэлектромеханических систем (УВЭМС) проводится на основе универсальной установки объединяющей системы “Г – МПТ”, “Г – АМ”, “Г – СМ”. Базой математического моделирования являются разработанные математические модели УВЭМС и программы на их основе [25] с использованием специализированных пакетов Mathcad, Matlab.

ММ непосредственных преобразователей энергии (НПЭ) строятся на основе разработанной концепции [2], суть которой состоит в представлении механизма управления НПЭ как процесса дискретного управления начальной фазой единственного гармонического колебания. Выходное напряжение U ( ω 2 t ) каждой фазы НПЭ при этом рассматривается как единственное гармоническое колебание с дискретно управляемой начальной фазой. Дискретность изменения фазы Δ φ =2 π / m определяется эквивалентным количеством фаз входного напряжения m , участвующих в формировании каждой фазы выходного напряжения (количеством пульсов входного напряжения в периоде выходного). На основе предложенной концепции введено понятие вектора фазового состояния (фазосмещения) (ФС), определяющего положение вектора выходного напряжения НПЭ на n -фазном симметричном ЭМП

0 ( t ) = e^jH [ t N

.

Все возможные способы управления при этом задаются во времени t переключающей функцией амплитуды h i ¹ [ t ] и фазы h j ² [ t ], а процедура преобразования электрической энергии n- фазного НПЭ при раздельном управлении описывается моделью

U2 (ш21 ) = H [t ]• Ui (to1t)

h 1 [ 1 ] =

h , [ 1 ]    0      0

0       h 22 [ 1 ]    0

... 0

... 0

0       0       h pp [ 1 ] ... 0

в ф а зе А; ABC – отключены ПЭ в фазе В ; ABC – отключены ПЭ в фазе С ; ABC – отключены ПЭ в фазах А, В, С . Введён оператор поворота

- 1 при повороте на - 2п/3-

0      0    0

... h nn [ ¹ ] _ -

w = <  0 при нулевом повороте-

;

+ 1 при повороте на +2п/3.

U 1 ( ® 1 1 ) = U m

sin ( rn , 1 + h 1² [ 1 ] • Аф ) sin ( to , 1 + h 2² [ 1 ] • Аф )

sin ( to 1 1 + h g [ 1 ] • Аф )

sin ( to , 1 + h m [ 1 ] • Аф ) ^;

^U 1 ⁽ ® 2 ¹ )

^U 2 ⁽ ® 2 ¹ )

U 2 ( ® 2 1 ) =

На базе теории обобщённого ЭМП, предложенной концепции и модели НПЭ, разработан математический аппарат решения задач анализа, синтеза и моделирования управляемых ВЭМС с НПЭ. При представлении математических моделей ЭМП в двухфазной системе координат α,β напряжения, синтезируемые НПЭ, также должны быть приведены к общей системе координат.

При заданных значениях переменных x α, x β с учётом введённого оператора поворота w значения переменных x 1 , x ’ в новой системе координат могут быть вычислены так:

Up ( ®21)

x а

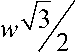
- 0.5

_^Un ( ® 2¹ ) .

^х в

.

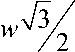
x e

Для НПЭ с однократной модуляцией (ОМ) переключающие функции в каждой фазе взаимосвязаны и равны:

H 2 [ 1 ] = H 2 [ 1 ] + mln H 2 [ 1 ] = H 2 [ 1 ] + 2 m/n

;                                                                                 .

Следовательно, задание всех управляющих воздействий в этих НПЭ возможно заданием закона изменения одной ПФ фазы. Выходное напряжение НПЭ представим в виде произведения ПФ амплитуды, m -мерного вектора гармонического колебания S ( ю , 1 ) = U_me^ ^ 1 ' и вектора ФС, т.е.

U (to21 ) = H1 [ 1 ] S (to,1)®(1)

При переключениях НПЭ имеет мгновенную несимметрию. Следовательно, его моделирование целесообразно проводить в трёхфазной системе координат, но это требует пересчёта значений переменных из трёхфазной системы координат в двухфазную и обратно. Для обобщённой записи такого перехода введены множители K A , K B B , K C , равные единице при совмещении соответствующей фазы A , B или C с осью α, и – нулю в противном случае. Введём матрицы перехода от трёхфазной системы координат к двухфазной и обратно

Р = = ¹ 23

K A       K B       K C

⁽ K C ^- K B ) ⁽ K A ^- K C ) ( K B ^- K A )

В случае трёхфазного выхода в соответствии с принятой концепцией НПЭ любой сложности, независимо от количества фаз m входного напряжения U ( ω 1 t ), принципов и способов управления, может быть задан минимальным количеством структур, соответствующих количеству возможных состояний тиристорного коммутатора : ABC–ПЭ во всех фазах ( А, В, С ) включены; ABC – отключены ПЭ

K A

C

K B

K B

K A

K C

K C

K B

K A

.

Для перехода из трёхфазной системы координат в двухфазную получим

x а

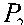
xb

xc

При обратном переходе значения переменных в трёхфазной системе координат x a , x b , x c находятся из системы уравнений

a

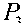
b

- 0.5

- 0.5

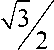
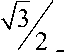
x а

Проведено обобщение и разработка ММ управляемых ВЭМС на базе машин постоянного тока, синхронных и асинхронных машин [2]. Задание переключающей функции h j ² [ t ] для НПЭ с ОМ определяется его характерной особенностью, состоящей в постоянстве шага переключения переключающих элементов НПЭ. Моделирование этих систем обеспечивается заданием цикла переключения n 1 и количества фаз входного напряжения, участвующих в формировании каждой фазы выходного напряжения. Мгновенное значение фазы входного гармонического колебания ω 1 t в момент коммутации изменяется на величину дискретности изменения начальной фазы Δ φ =2 π / m . На рис. 3-5 в качестве примера приведены результаты моделирования с использованием (1) – (9) системы “НПЭ – АМ” с ОМ.

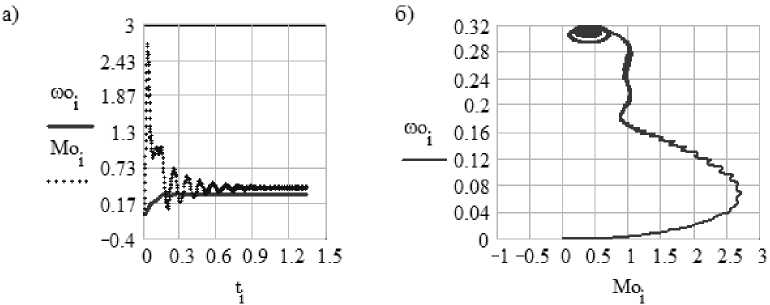
Рис. 3. Переходная характеристика момента и скорости (а), динамическая механическая характеристика (б) системы «НПЭ – АМ» при ОМ n 1=45 ( m =6) при f 2 =16,667 Гц, двигатель АО2 – 31 – 4

Взаимосвязь параметров НПЭ при заданных количествах шагов N на периоде T 1 входного m -фазного напряжения и n 1 в цикле переключения переключающей функции фазы h j ² [ t ] с дискретностью Δφ определяется формулами

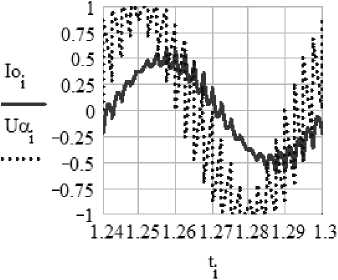
Рис. 4. Зависимости напряжения U α , тока I 0 , потокосцепления ψ α от времени n 1=45 ( m =6), f 2 =16,667 Гц, двигатель АО2 – 31 – 4

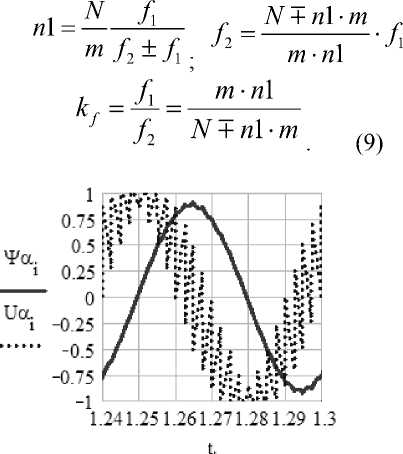
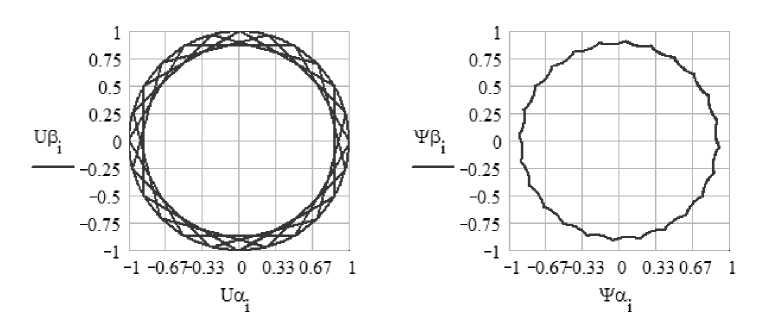
Рис. 5. Годографы напряжений U , и потокосцепления ψ α статора n 1=45 ( m =6), f 2 =16,667 Гц, двигатель АО2 – 31 – 4

Выводы: совокупность разработанных математических моделей, программных средств, экспериментальных установок, методического обеспечения по исследованию ЭМП, вентильных преобразователей и управляемых вентильно-электромеханических систем на их основе образует интегрированный электромеханический комплекс – элемент, обеспечивающий научные и учебные исследования УВЭМС.