Интегрируемые нестационарные модели в системах навигации
Автор: Богословский С.В.
Журнал: Научное приборостроение @nauchnoe-priborostroenie
Рубрика: Оригинальные статьи
Статья в выпуске: 4 т.14, 2004 года.
Бесплатный доступ
Рассматриваются нестационарные математические модели систем навигации и их элементов, допускающие решение задачи Коши в замкнутой форме. Применение интегрируемых нестационарных моделей позволяет расширить возможности аналитических методов исследования, хорошо разработанных для стационарных моделей. Аналитические методы позволяют установить тонкую структуру решения задачи Коши, условий устойчивости и законов управления для нестационарных систем.
Короткий адрес: https://sciup.org/14264360
IDR: 14264360 | УДК: 531.768(088.8)+538.65+621.316.73
Текст научной статьи Интегрируемые нестационарные модели в системах навигации
Аналитические методы исследования систем автоматического управления требуют глубокого осознания исследователем сущности процессов управления, позволяют повысить эффективность использования компьютера и рабочего времени, придать наглядность и убедительность получаемым результатам, правильно поставить задачу для полномасштабного численного исследования с использованием современного программного обеспечения и получить уверенность в полноте выполненного исследования. Трудности использования аналитических методов в настоящее время успешно преодолеваются повсеместным распространением вычислительной техники и использованием математического обеспечения для выведения громоздких формул. Возможности современной вычислительной техники позволяют в реальном времени выявлять свойства исследуемых систем, влияющие на выбор необходимого для исследования математического аппарата.
Задачи учета изменений во времени коэффициентов математической модели впервые возникли при решении следующих задач автоматизации управления динамическими объектами:
-
— разгон на участке старта до скорости движения на основном участке траектории;
-
— выведение в заданную точку с заранее заданными значениями параметров движения;
-
— сближение с неподвижной или подвижной посадочной платформой;
-
— мягкая посадка космических аппаратов;
-
— вертикальный взлет и посадка самолетов (летательных аппаратов, ЛА);
-
— управление строем самолетов;
-
— межсамолетная навигация;
-
— стыковка космических аппаратов;
— выведение динамических объектов на заданную траекторию.
Дальнейшее развитие науки и техники привело к внедрению нестационарных алгоритмов управления поездами на магнитной подвеске и решению задач аэромагнитного моделирования [1].
Для решения этих задач во второй половине XX века активно разрабатывались аналитические методы исследования динамики нестационарных систем [2, 3]. Наиболее известными из этих методов являются метод Заде—Солодовникова, метод Гринстеда и метод интегрируемых изображений. Метод Заде—Солодовникова представляет собой в достаточной мере универсальный алгоритм получения приближенных выражений в виде рядов для параметрических передаточных функций систем с полиномиальными коэффициентами. Метод Гринстеда позволяет заменять уравнения с переменными коэффициентами уравнениями с квази-фиксированными коэффициентами.
Метод интегрируемых изображений основан на решении дифференциальных уравнений в области изображений и получении на этой основе точного интегрального представления для параметрической передаточной функции. В настоящее время метод интегрируемых изображений использует аппарат построения точного решения систем линейных дифференциальных уравнений, приводимых в изображениях к обыкновенному дифференциальному уравнению Лапласа [4]. Перспективы развития метода связаны с получением в изображениях дифференциальных уравнений (около 1500 уравнений), интегрируемых в замкнутой форме [5].
Приведем краткий обзор уже внедренных в практику проектирования интегрируемых нестационарных моделей и областей их возможного применения в системах навигации. Классификация наиболее известных методов исследования линейных нестационарных систем дана в табл. 1.
В данной работе основное внимание уделяется применению и дальнейшему развитию метода интегрируемых изображений. Это направление отличается от других методов меньшей универсальностью,
Табл. 1. Классификация методов решения линейных нестационарных уравнений по их содержанию
|
Содержание метода Название метода |
Точное решение |
Последовательные приближения |
Разложения в ряды |
Понижение порядка |
Аппроксимация нестацио-нарностей |
|
Интегрируемых |
|||||
|
изображений |
+ |
+ |
+ |
+ |
— |
|
Гринстеда |
— |
— |
— |
— |
+ |
|
Заде—Солодов- |
|||||
|
никова |
— |
+ |
+ |
+ |
— |
Табл. 2. Классификация инновационных задач по содержанию методов решения задачи Коши
|
Содержание метода Инновационные задачи |
Точное решение в замкнутой форме |
Последовательные приближения |
Разложения в ряды |
Понижение порядка |
Глобальная линеаризация |
|
Разгон на участке старта |
— |
+ |
+ |
— |
+ |
|
Наведение ЛА с земли |
+ |
— |
+ |
+ |
— |
|
Самонаведение |
+ |
— |
+ |
+ |
— |
|
Сближение |
+ |
— |
+ |
+ |
— |
|
Мягкая посадка |
+ |
+ |
+ |
— |
+ |
|
Вертикальный взлет |
+ |
+ |
+ |
— |
+ |
|
Управление строем ЛА |
+ |
— |
+ |
+ |
— |
|
Межсамолетная навигация |
+ |
— |
+ |
— |
— |
|
Стыковка |
+ |
— |
+ |
+ |
— |
однако во многих случаях позволяет получать точное решение задачи Коши. Перспективность этого направления обеспечивается новыми возможностями, которые предоставляют машинные программы получения аналитических выводов, например программа Mathematica.
Классификация методов решения различных задач на основе рассматриваемого в работе подхода приведена в табл. 2.
В данной работе рассматривается получение решений для двух задач: нестационарного управления заходом на посадку ЛА и управления бесконтактным подвесом тела.
МОДЕЛЬ ЗАХОДА ЛА НА ПОСАДКУ
Основное внимание в работе уделено проблематике и подходам к решению задач анализа и синтеза применительно к системам нестационарного управления с известными аналитическими решениями задачи Коши в области изображений. В качестве примера применения модели с особой точкой рассмотрим систему нестационарного управления заходом на посадку летательного аппарата и нестационарного управления уклонением от препятствий. На этих этапах полета происходит значительное изменение параметров тра- ектории полета (высоты, курса и др.), конфигурации летательного аппарата (выпуск закрылков, щитков, интерцепторов и др.). При этом летчик должен наблюдать за показаниями большого количества приборов и на основе этих показаний принимать решения и управлять системами и подсистемами самолета.
Общеизвестна сходность этих задач с задачами управления эквидистантным движением микрозонда сканирующего туннельного микроскопа (СТМ) над изучаемой поверхностью в нанотехнологии.
Рассматриваемые в работе системы нестационарного управления с особой точкой существенно отличаются от стационарных систем автоматического управления наличием используемой для формирования сигнала управления нестационарной кинематической зависимости между углом места и текущей дальностью до особой точки траектории.
Системы нестационарного управления являются важной разновидностью нестационарных систем. Если понятие "нестационарные системы" охватывает все возможные варианты нестационарно-сти, такие например как учет влияния изменения скорости на аэродинамические характеристики динамического объекта, то в системах нестационарного управления учитывается только неста-ционарность, которая связана, например, с изменением дальности до глиссадного радиомаяка (ГРМ) в процессе формирования управляющего сигнала.
В уравнения управления входит и функция цели управления, определяющая движение по заданной траектории. Пусть, например, цель маневрирования к заданному положению в вертикальной плоскости соответствует схеме рис. 1.
На рис. 1 приняты следующие обозначения: ЛА, ГРМ — текущие положения самолета и посадочной платформы (совмещенной с ГРМ) соответ-
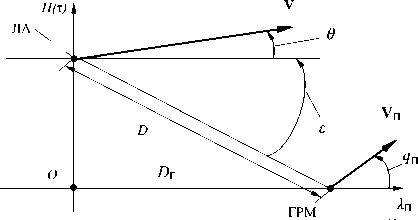
Рис. 1. Схема цели наведения в вертикальной плоскости ственно; D — текущее значение наклонной дальности до ГРМ; Dг — текущее значение горизонтальной дальности до ГРМ (по оси λП); V — вектор скорости ЛА; θ — угол между вектором скорости ЛА и горизонтом; Vп , qп — вектор скорости и угол между вектором скорости перемещения посадочной платформы с размещенным на ней ГРМ (для случая посадки на летающую платформу) и горизонтом; H — высота полета ЛА относи-H тельно посадочной платформы; ε = arctg — Dг угол визирования ГРМ в вертикальной плоскости (угол наклона линии ЛА—ГРМ, или угол места ГРМ).
Тогда функция цели управления может быть представлена в виде
Uц(D,ε,θ,qп)=0, где Uц(D,ε,θ, qп) — функция цели управления, параметры которой определяются кинематическими соотношениями:
dε
D = - V sin( θ - ε ) + V sin q ;
dt dD dt
- V cos( θ - ε ) + V п cos q п .
Для некоторых из методов маневрирования функция цели управления известна [2, 6]:
U ц( D , ε , θ , q п) = θ - ε — метод погони;
U ц( D , ε , θ , q п) = θ - ε + ϑ y — метод погони с упреждением;
U ц( D , ε , θ , q п) = θ - k ε — метод пропорциональной навигации;
U ц( D , ε , θ , q п) = ε - ε 0 — метод параллельного сближения.
В связи с развитием методов аналитического исследования нелинейных систем дифференциальных уравнений может быть предложен метод точечной линеаризации , который заключается в замене модели нелинейного элемента переменным точечным коэффициентом усиления . Точечный коэффициент усиления вычисляется в процессе решения задачи Коши на ЭВМ как отношение выходного и входного сигналов нелинейного элемента для заданного воздействия на входе нелинейной системы автоматического управления. Метод точечной линеаризации можно использовать при любой заданной форме отличных от нуля сигналов на входе нелинейной системы. Использование этого метода линеаризации позволяет решать каждую конкретную задачу Коши для нелинейной системы, каждый раз находя свои подходящие аппроксимации нелинейных зависимостей изменяющимися во времени коэффициентами.
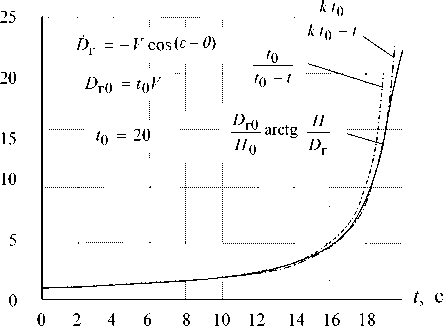
Рис. 2. Аппроксимация нелинейности нестационарным коэффициентом усиления
Точечный коэффициент усиления нелинейного элемента может быть вычислен для нескольких отличных от нуля типовых возмущающих воздействий на систему. В результате этого может быть получено некоторое множество реализаций зависимости точечного коэффициента усиления от параметров входного сигнала, вида нелинейной функции и параметров передаточных функций линейных звеньев.
УРАВНЕНИЯ МОДЕЛИ ЗАХОДА НА ПОСАДКУ
Для системы уравнений, характеризующей заход на посадку по линии визирования, в качестве возмущающего воздействия примем начальное значение высоты полета H 0 = 100 м. Исследуем отношение выходного сигнала к входному для кинематической нелинейности обратной связи:
H ε = arctg , Dг где ε — угол наклона линии визирования; H, Dг — высота полета и текущее значение горизонтальной дальности до ГРМ соответственно.
Высоту полета определим как первую координату решения системы уравнений шестого порядка при начальном условии H (0) = H 0 . Горизонтальную дальность определим по формуле
t
Dг = Dг0 -V∫cos [ε(ξ)-θ(ξ)]dξ, t0
где D г0 — начальное значение дальности до ЛА;
-
V , ε , θ — скорость ЛА, угол визирования ЛА и угол наклона вектора скорости соответственно.
На рис. 2 сплошной линией показано отношение выход/вход (точечный коэффициент усиления) нелинейной зависимости Z ( H, D ) =
DH
= г0 arctg , а пунктирной — его аппроксима-
H0 Dг ция нестационарной функцией времени 0
t 0 - t
.
Как следует из рис. 2, нестационарная аппроксимация точечного коэффициента усиления функ- t цией времени t0
-
t в рассмотренном примере с погрешностью до 10% аппроксимирует отноше-DH ние выход/вход г0 arctg для нелинейности
H0 Dг типа арктангенса на протяжении 90 % интервала времени функционирования системы. Очевидно, что можно добиться и большей точности, варьируя значение t0 пропорционально его номиналь- ному значению, указанному на рисунке.
Так, полагая для аппроксимации t 0 = k t 0н , где t 0н = 20 и k ≈ 1.015, можно уменьшить погрешность аппроксимации до 1 % на интервале [0, k t
-
19] секунд. Кривая 0 при k ≈ 1.015 показана
k t0 - t на рис. 2 штрихпунктирной линией. На интервале [0, 19] секунд эта кривая практически неотличима от точной нелинейной зависимости, изображенной на рис. 2 сплошной линией.
Таким образом, использование метода точечной линеаризации в рассмотренном примере системы уравнений шестого порядка позволяет привести нелинейную систему к линеаризованной системе с переменным коэффициентом, допускающим применение аналитических методов решения задачи Коши на 95 % длины интервала интегрирования.
В качестве идеальной системы маневрирования к заданному положению может рассматриваться безынерционная нестационарная динамическая система, структурная схема которой представлена на рис. 3.
Передаточная функция от выхода нестационарного звена до выхода по первой координате может α быть представлена в виде Wz1(p) = 1 (рис. 3, а), p где коэффициент α1 определяет метод маневрирования к заданному положению: при α1 = 1 получаем метод погони, который соответствует равенству угла θ наклона вектора скорости углу ε наклона линии визирования (θ = ε); при α1> 1 —
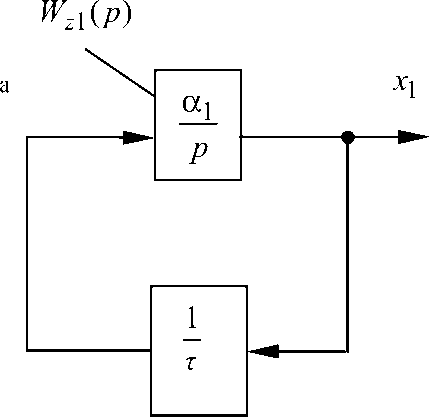
б
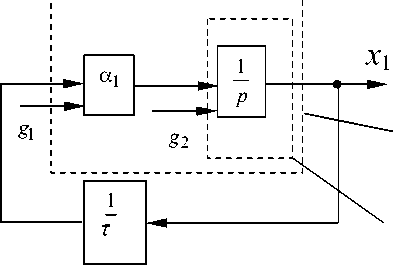
W 1 ( p )
W 2 ( p )
Рис. 3. Блочно-операторная структура идеальной динамической системы нестационарного управления: а — идеальная система без учета возмущений; б — схема учета возмущений метод пропорциональной навигации (0 = а1 е ); при а1 = 1 и g 1 = Sy — метод погони с упреждением.
Рассмотрим модель траектории идеального ЛА при учете возмущений в виде начального отклонения линейной координаты от заданной траектории (рис. 3, б).
Модель переходных процессов в идеальной системе без учета обнуления сигнала с выхода нестационарного звена
Предположим, что отсутствует обнуление начального значения сигнала на выходе нестацио нарного звена (в реальной системе это эквивалентно отсутствию обнуления сигнала на входе глиссадного радиоприемника).
Начальное значение первой координаты определяется ее отклонением от заданной траектории в начальный момент времени. Если заданная траектория — прямая линия, то изменение первой координаты в отклонениях от прямой линии можно представить в виде
τ x i( t) = П( t) - —x 1(0), (1)
t о где n(t) — отклонение первой координаты от требуемой прямой линии в переходном процессе; x 1 (0) — начальное отклонение первой координаты от заданной прямой линии; - = t -t0; t, t0 — текущее и полное время маневрирования соответственно. Тогда для переменной п начальные условия будут нулевыми. Это позволяет воспользоваться известным математическим аппаратом для решения задачи Коши [4]. В частности, для идеальной системы (рис. 3, а) получим:
а '
Х 1 ( t ) = X 1 (0)j( t -) Or. (2)
Формула (2) представляет собой модель поведения идеальной системы без обнуления сигнала с выхода нестационарного звена.
Графики переходных процессов в идеальной системе без обнуления начального значения сигнала с выхода нестационарного звена ( g 1 ( p ) ^ 0) при различных значениях а 1 , рассчитанные по формуле (2), представлены на рис. 4.
Из рис. 4 следует, что при а > 1 траектория захода на посадку без обнуления начального значения сигнала с выхода нестационарного звена располагается ниже желаемой прямолинейной траектории и существует опасность преждевременного приземления ЛА.
Модель переходных процессов в идеальной системе с обнулением сигнала с выхода нестационарного звена
Более предпочтительным по сравнению с предыдущим является закон управления, предполагающий заход на посадку по траектории, располагающейся выше заданной прямолинейной траектории. Это обеспечивается введением в закон управления обнуления начального отклонения сигнала с выхода нестационарного звена.
Выражение для переходного процесса с обнулением выходного сигнала нестационарного звена идеальной астатической системы маневрирования:
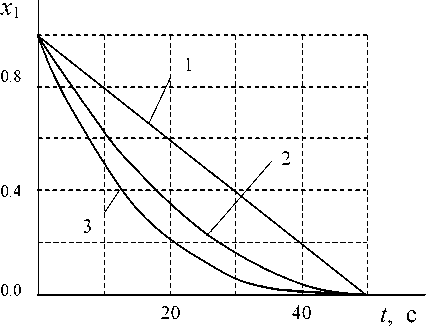
Рис. 4. Переходные процессы в идеальной системе без обнуления начального значения сигнала с выхода нестационарного звена: 1 — при а1 = 1; 2 — при а1 = 2 ; 3 — при а1 = 3
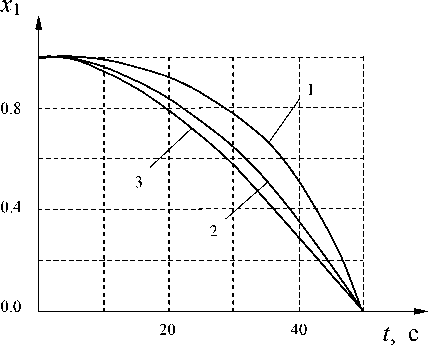
Рис. 5. Переходные процессы в идеальной системе с обнулением начального значения сигнала с выхода нестационарного звена: 1 — при а1 = 1; 2 — при а1 = 2 ; 3 — при а1 = 3
Как следует из рис. 5, при обнулении начального значения сигнала с выхода нестационарного звена траектории идеального ЛА располагаются выше желаемой прямолинейной траектории и тем ближе к ней, чем больше коэффициент а усиления прямой цепи.
МОДЕЛЬ БЕСКОНТАКТНОГО ТРАНСПОРТНОГО СРЕДСТВА
Системы бесконтактного подвешивания динамических объектов находят все большее применение в современных высокотехнологичных продуктах производства — от микромеханических гироскопов до высокоскоростных транспортных средств. Бесконтактные транспортные средства обычно моделируются уравнениями невысокого порядка, что обусловлено наличием непреодолимых проблем с получением аналитического решения для уравнений более высокого порядка, имеющих существенную нелинейность.
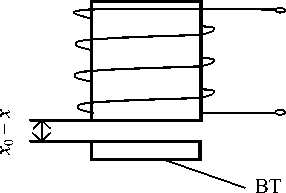
Функционально-структурные схемы электромагнитного и электростатического бесконтактных подвесов представлены на рис. 6, а и б соответственно [1].
На рис. 6 приняты следующие обозначения: ЭМ — электромагнит; I — сила тока; ВТ — взве- а
x . ( t ) = ' :0:' ; i + Л T x . (0).
1 - а 1 ( t о ) а 1 - а 1 t 0
б
В частности, при а 1 = 2
( x Д t) = x 1(0) 1
2 А t
.
I t0 ,
Графики переходных процессов с обнулением
и
5?
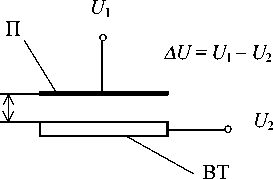
Рис. 6. Схемы бесконтактных подвесов: а — электромагнитный подвес; б — электростатический подвес
начального значения сигнала с выхода нестацио-
нарного звена при различных значениях а 1 , рассчитанные по формуле (3), представлены на рис. 5.
шенное тело; U 1 и U 2 — электрические потенциалы, подаваемые на пластину П конденсатора и на ВТ, соответственно; A U — разность потенциалов; ( x 0 - x ) — зазор между ЭМ (П) и ВТ.
В реальных системах бесконтактного подвешивания обобщенная координата может зависеть от многих переменных величин, каждая из которых моделируется своим многомерным дифференциальным уравнением. В этих случаях единственным методом сведения исходной нелинейной модели к интегрируемому виду является линеаризация. Один из известных методов линеаризации нелинейных моделей — замена аргумента нелинейной функции известной функцией времени и последующее определение коэффициентов линеаризации. Однако линеаризованная система оказывается нестационарной. Задача состоит в получении такой линеаризованной модели, которая допускает возможность аналитического решения задачи Коши.
Рассмотрим возможный метод приведения нелинейной математической модели бесконтактного подвеса к интегрируемому виду линейной нестационарной модели с особой точкой.
Известно, что сила взаимодействия взвешенного тела (ротора) и статора для одностепенных электромагнитных ( F M) и электростатических ( F Э) бесконтактных подвесов транспортных средств определяется соотношениями [7]
F М
ЦЦ 0 $ m w 2I 2 , 8( x 0 - x )2
2 ее 0 A c A U2
( x о - x ) 2 ’
где ц , ц 0 — относительная и абсолютная магнитные проницаемости соответственно; е , е 0 — относительная и абсолютная диэлектрические проницаемости соответственно; w — число витков электромагнита; S m , S c — площадь полюса электромагнита и эквивалентной обкладки конденсатора соответственно; I — сила тока в обмотке электромагнита; A U — разность потенциалов на взвешенном теле и на статоре; x 0 - x — величина зазора между взвешенным телом и электромагнитом (обкладкой конденсатора); x , x 0 — координата взвешенного тела в текущий и в начальный моменты времени соответственно.
Обобщая формулы (4) и (5), представим зависимость силы бесконтактного (электромагнитного или электростатического) взаимодействия взвешенного тела с силовым полем в виде
F = z aq ,2 = af i ( x ) q 2 , (6) ( x о - x )
где a — постоянный коэффициент, зависящий от конструкции бесконтактного подвеса; f , ( x ) =
=------- 2- ; q — обобщенное управляющее воз-
( x о — x )
действие (сила тока или разность потенциалов).
Для эффективного исследования системы управления необходимо построить математическую модель, учитывающую нелинейную зависимость (6) силы F от координат ( x и q) и позволяющую получить аналитическое решение.
Для решения этой задачи линеаризуем входящее в формулу (6) обобщенное управляющее воздействие q в окрестности его равновесного значения q 0
q 2 = q о 2 + k q q , (7)
а нелинейную функцию f1 (x) аппроксимируем дробно-линейной функцией f2 =
x 0 ( x 0 — k x x )
Коэффициенты линеаризации kq и kx подлежат определению, например, как отношение вы-ход/вход при известном входном воздействии. Коэффициенты линеаризации могут быть определены на этапе предварительной аппроксимации нелинейностей с использованием аналитического решения задачи Коши.
В качестве первого приближения к значению коэффициента kq можно принять коэффициент линеаризации нелинейности q 2 первыми двумя членами ряда Тейлора в окрестности равновесного значения kq = 2 q 0 .
В качестве первого приближения к значению коэффициента kx в формуле (8) можно принять значение kx = 1.38, обеспечивающее удовлетворительную аппроксимацию нелинейной функции f1 (х) дробно-линейной функцией f2 (х) на интервале возможных значений аргумента. Графики аппроксимации нелинейной функции f, (x) = x2
=------- 2" (пунктирная кривая) дробно-линейной
( x 0 — x )
функцией f 2 ( x ) =--- x 0--- (сплошные кривые)
( x 0 — k x x )
при kx = 1.38 и kx = 1.25 показаны на рис. 7.
Из рис. 7 следует, что аппроксимирующая дробно-линейная функция f2(x) при kx = 1.38 на большей части области возможных значений аргумента отличается от аппроксимируемой образуется к виду
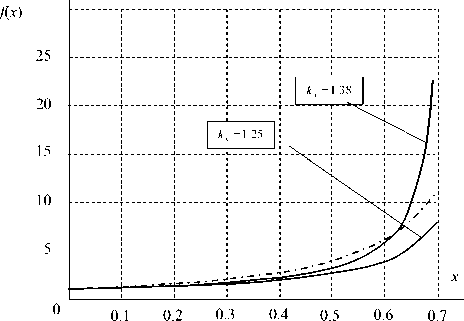
Рис. 7. Аппроксимация нелинейной функции дробно-линейной функцией
F =
a xO(x0 - kxx)
( q o 2 + k q q ).
Модель (9) содержит произведение линейной функции от q на величину, обратно пропорциональную (x0 – kxx). При линеаризации нелинейной модели (9) предположим, что координата х линейно зависит от времени x = vt, (10)
где ν — параметр, подлежащий определению из условия оптимальной аппроксимации переходных процессов. С учетом аппроксимации (10) модель (9) приобретает вид, допускающий получение интегрального представления решения задачи Коши:
a ( q 2 + k q q ) = kF o + kF 1 q x o ( k x vt - x o ) ( t - t o ) ( t - t o ) ,
нелинейной функции f 1 ( x ) не более чем на 20 %.
С учетом аппроксимаций (7) и (8) модель пре-
aq где kFo =- -----; kF 1
kxvx 0
akq
; t o = k vx k v x 0
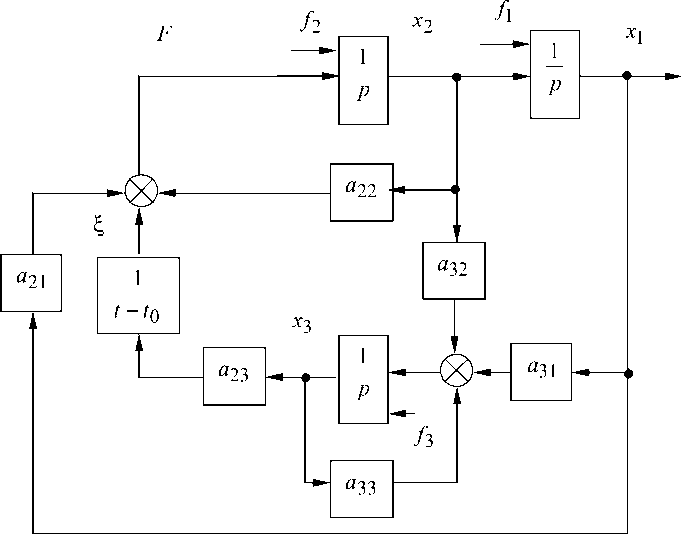
Рис. 8. Структурная схема нестационарной модели бесконтактного транспортного средства
Структурная схема нестационарной модели бесконтактного транспортного средства приведена на рис. 8. Модель (11) позволяет учесть нестацио-нарность силового поля и включает три неопределенных параметра: k F 0, k F 1 и t 0 , зависящих от трех неопределенных коэффициентов q 0 , ( k x v ) и kq . Конкретные типы моделей такого вида используются при моделировании переходных процессов в акселерометрах и гироскопах с магнитным [7] и электростатическим подвесами [8], в двигателях для высокоскоростных транспортных средств на магнитной подвеске.
В общем случае с учетом (11) линеаризованная модель бесконтактного подвеса транспортного средства с учетом нестационарности силового поля может быть представлена системой уравнений
лина—Бромвича
х ( р ) = [ x 1 ( р X
...
x = x 2 + f i l
x 2 = a 21 x 1 + a 22 x 2 + a 23 t
x 3
t 0
+ f 2 ;
x 3 = a 31 x 1 + a 32 x 2 + a 33 x 3 + f 3 ,
где f 1 , f 2 , f 3 — возмущающие воздействия, в том числе зависящие от начальных условий; x 1 , x 2 , x 3 — координаты вектора состояния системы, приведенные к нулевым начальным условиям; х 1 — координата линейного смещения взвешенного тела; x 2 — скорость линейного смещения; x 3 = q — отклонение от равновесного значения силы тока в электромагнитной катушке или разности потенциалов A U ; a ij — постоянные коэффициенты, i = 2,3; j = 1,2,3.
В такой постановке для решения системы уравнений (12) может быть использован метод, аналогичный методу решения обыкновенного дифференциального уравнения Лапласа с особой точкой [1]. Третье уравнение системы (12) составлено в предположении, что управляющее воздействие является взвешенной суммой всех трех обобщенных координат. Преобразуем второе уравнение, умножив его на т = t - t 0 и заменив координату x 2 в соответствии с первым уравнением системы (12):
x 1 = x 2 + f 1 ;
t ( x 1 — a 21 x 1 — a 22 ■ x 1 ) = a 23 x 3 + т ( f 2 — a 22 f [ ); (13)
x 3 = a 31 x 1 + a 32 x 1 + a 33 x 3 + f 3 — a 32 f 1 ,
Предположим, что требуется найти решение систем уравнений (12) и (13) при нулевых начальных условиях, т. е. эти системы уравнений составлены в отклонениях от равновесного положения. Тогда решение системы уравнений (13) будем искать в виде интеграла обращения Римана—Мел-
в c + i ^
X ( t ) = — |> X ( p )d p , 2 ra
, x n ( P )]T
где
c — i ^
— преобразование Лап-
ласа векторной функции X ( t ) = [ x 1 ( t ),
I ...
, x „ ( t )]T со-
стояния системы.
Относительно изображения координаты x 1 при нулевых начальных условиях может быть составлено дифференциальное уравнение
V
d V
— + t 0 [( P d P
= a 23 x 3 ( Р ) —
где
a 21
Pa 22 ) x 1 ( Р )] =
V
+ t 0 [ f 2 ( Р ) — a 22 f l ( Р )], d p
x 3 ( Р ) =
= ( pa 32 + a 31 ) x p )
Р — a 33
+ —1— [ f 3 ( p ) — a 32 f , ( p )].
Р — a 33
Представим это уравнение в более компактной форме:
d , .
— x 1 ( Р ) = d p
—
•
to + Wz i( P) + Q^
0 z Q ( p )
x 1 ( р ) — F^( р X (14)
где
W z 1 ( Р ) =
a 23 ( Pa 32 + a 31 )
( P — a 33 )( P 2 — a 21 — Pa 22 )
переда-
точная функция стационарной части системы от выхода нестационарного звена с координатой ^ до
входа этого звена;
Q ( Р ) = ( Р 2 — a 21 — pa 22)— характеристический
полином подсистемы с координатами x 1 , x 2 с исключенной нестационарной обратной связью;
F S 1 ( Р ) =
a 23 [ f 3 ( Р ) — a 32 f 1 ( Р )]
( Р — a 33 )( Р 2 — a 21 — Р • a 22 )
V
d
— + t 0 [ f 2 ( Р ) — a 22 f l ( Р )] ( Р — a 33 ) d p ) _______________
( Р — a 33 )( р2 — a 21 — р ■ a 22 )
— взве-
шенная сумма внешних воздействий, приведенная к входу, на который подается сигнал нестационарного звена.
При нулевом начальном условии общее реше-
ние совпадает с частным решением (с реакцией системы на возмущение ^( p )) и имеет вид [4]:
- c + i 1
х' p e " pTQ (p )WZ, (p) ф -1 (p) J e — ф( z )d z 1 Q(z) d p. Выражение, стоящее в квадратных скобках формулы (15), представляет собой параметрическую передаточную функцию линеаризованной нестационарной системы управления бесконтактным транспортным средством по воздействию с изображением F1 (p): Ti( p, т) = e- pTQ (p )WZ i( p) ф-1( p) x p x fez"-----ф(z)d z. 1 Q (z) Учитывая, что в магнитном подвесе отклонения ВТ от среднего значения, как правило, весьма небольшие по сравнению с величиной зазора, для больших значений 10 и т можно получить приближенное выражение для параметрической передаточной функции (16) Ti(p,т ) = WД p,т ) = = Q ( p )WZ i( p) - т - т + W 1(p) + Q (p ) , Q (p ) где Q(p) — характеристический полином стационарной части системы с исключенной нестационарной обратной связью; Wz 1 (p) — передаточная функция стационарной части системы от выхода нестационарного звена до входа этого звена. Например, для системы рис. 8 в соответствии с формулой (14) Q (p ) = (p2 -a 21 -pa 22); Wz 1( p ) = а23 ( pa32+ a31) . (p - азз)(p - а21 - pa22) Приближенное выражение (10) достаточно точно при т< 0.510, т. е. как раз в рабочей области значений т. В этой же области значений функция, обратная квадрату т, хорошо аппроксимируется функцией, обратной первой степени т (рис. 7), что подтверждает адекватность нелинейной и линеаризованной математических моделей. Движение транспортного средства в вертикальной плоскости в общем случае происходит под действием управляющего воздействия, демпфирующих и гравитационных сил. Состояние статического равновесия в бесконтактных подвесах в соответствии с теоремой Ирншоу является неустойчивым, поэтому система подвешивания работает в режиме установившихся колебаний с достаточно малой амплитудой. Работа системы происходит следующим образом. Управляющее воздействие F (рис. 8) приводит ВТ в движение во взвешенном состоянии. В момент времени t = t, соответствующий достижению координатой %1 заданного значения х*, параметры управляющего воздействия q0 и kq изменяются так, что система начинает движение в обратном направлении. После достижения первой координатой значения х1 = х0 восстанавливаются параметры управляющего воздействия, соответствующие движению ВТ в прямом направлении, и цикл повторяется. Таким образом, решение задачи Коши получено в замкнутой форме и сведено к вычислению интегралов типа (15). ЗАКЛЮЧЕНИЕ Применение теории интегрируемых изображений позволило получить аналитические зависимости для исследования различных динамических систем: аппроксимации переходных процессов в системе захода ЛА на посадку и параметрические передаточные функции для транспортного средства с магнитной подвеской. Модель бесконтактного подвеса может быть отнесена к классу моделей линейных нестационарных систем управления с особой точкой. Модель может быть использована для анализа и синтеза недифференциальных схем систем управления гироскопами на магнитном подвесе в навигационных системах и бесконтактными транспортными средствами. Аналогично могут быть исследованы и системы уравнений состояния достаточно высокого порядка, моделирующие движение динамических объектов в магнитном поле.
Список литературы Интегрируемые нестационарные модели в системах навигации
- Богословский С.В. Модель бесконтактного транспортного средства как системы с особой точкой//Научное приборостроение. 2003. т. 13, № 2. C. 54-61.
- Барабанов А.Т. Методы исследования систем с переменными коэффициентами//Методы исследования нелинейных систем автоматического управления/Под ред. Р.А. Нелепина. М.: Наука, 1975. 448 с.
- Пупков К.А., Егупов Н.Д., Коньков В.Г. Методы анализа, синтеза и оптимизации нестационарных систем автоматического управления/Под ред. Н.Д. Егупова. М.: МГТУ им. Н.Э. Баумана, 1999. 684 с.
- Богословский С.В., Богословский В.С. Динамика нестационарных систем с равномерно изменяющимися во времени коэффициентами//Научное приборостроение. 2002. т. 12, № 3. C. 56-67.
- Камке Э. Справочник по обыкновенным дифференциальным уравнениям (пер. с нем., 5-е изд.). М.: Наука, 1976. 576 с.
- Зубов В.И. Лекции по теории управления. М.: Наука, 1975. 496 с.
- Сапожников Г.А., Богословский С.В., Кизимов А.Т. Теория и практика измерительных электромагнитных подвесов. СПб.: СПб ГУАП, 2001. 384 с.
- Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения. М.: Наука, 1985. 231 с.


