Интегрирующий АЦП с компенсацией погрешности от краевых эффектов

В настоящее время самые высокоточные АЦП напряжения строятся на принципе промежуточного компенсационного интегрирующего преобразования напряжения в сигнал одного из видов импульсной модуляции - ШИМ, ЧИМ, ФИМ, ИРМ (импульсно-разностной мо- дуляции), КИМ (кодоимпульсной модуляции). Промежуточный сигнал суммируют в течение примыкающих циклов преобразования, длительность которых во много раз превышает период импульсной модуляции. Чем больше время преобразования, тем потенциально более высокая разрешающая способность может быть достигнута. Однако на этом пути есть серьезные ограничения, связанные с рядом методических и инструментальных погрешностей, из которых одной из основных является так называемая погрешность от краевых эффектов [1].

Рис. 1. Обобщенная структурная схема (а) и временные диаграммы работы (б) интегрирующих АЦП. ФВФ₀ – формирователь весовой функции g_o ( t ), П_o – перемножитель опорного напряжения U_o на функцию g_o ( t ), П _х - перемножитель преобразуемого напряжения U_x на функцию g_x ( t ), ФВФ _х – формирователь весовой функции g_x ( t ), И – интегратор, УС – устройство сравнения, ФПУ – формирователь порогового уровня, УУ – устройство управления, ЦИ – цифровой интегратор (счетчик импульсов), ГОЧ – генератор опорной (тактовой) частоты

Определение погрешности от краевых эффектов

Рассмотрим природу возникновения этой погрешности на примере обобщенной функциональной схемы интегрирующего АЦП (рис. 1а), в которой может быть реализован любой вид импульсной модуляции.

Процессы, происходящие в ИАЦП, поясняются временной диаграммой на рис.1б. Конкретный вид диаграммы зависит от вида импульсной модуляции, реализуемой в ИАЦП. В рассматриваемом случае реализуется фазоимпульсная модуляция. Формирователь порогового уровня изменяет полярность порогового напряжения (на диаграмме соответствующая осциллограмма обозначена как 8′) всякий раз, как выходное напряжение интегратора (на диаграмме оно обозначено как 6′) достигает порогового уровня. Однако это происходит не сразу после срабатывания устройства сравнения, а в момент прихода первого после срабатывания импульса тактовой частоты. Эти моменты времени отмечены на диаграмме вертикальными прямыми в виде точек. Весовая функция g_o ( t ) синхронно с изменением порогового уровня меняет знак своего значения (по модулю оно равно единице), в результате чего изменяется полярность опорного напряжения, поступающего на вход сумматора с выхода перемножителя П_о.

Уравнение преобразования ИАЦП может быть представлено в следующем виде:

1 t к                                   1 t к

— j g x ^{( t ) u} x ^(t)dt ■     |"g о ^{( t ) U} о dt =

τ о_{t н}                            τ о_{t н}

= I ( t к ) - I ( t н )

где u_x ( t ) – преобразуемое напряжение; U_o – опорное напряжение; τ_о – постоянная времени интегратора; g_x ( t ) и g_o ( t ) – весовые функции; t_н и t_к – моменты начала и конца интервала интегрирования (времени преобразования); I ( t_н ) и I( t_к ) – значения выходной величины интегратора в начале и конце времени преобразования ИАЦП.

Для простоты в рассматриваемом алгоритме весовая функция g_x ( t ) имеет постоянное значение, равное 1, в результате чего ИАЦП имеет амплитудно-частотную характеристику вида │ Sin ω ( t_к – t_н )/ ω ( t_к – t_н )│, где ω – частота входного воздействия [1]. Такая АЧХ имеет нули на частотах, кратных частоте 1/( t_к – t_н ), что обеспечивает подавление помех с частотами, равными и кратными этой частоте.

Наличие в правой части уравнения (1) разности I(tк) – I(tн) является источником погрешнос- ти, которую принято называть погрешностью от краевых эффектов. На выходе цифрового интегратора формируется результат преобразования, выражаемый следующим соотношением, получающимся путем разрешения уравнения (1) от-tк носительно выходной величины Jдо (t)dt: tн tк                                    tк fgo (t )dt = - — fgx (t )u x (t )dt +    I (tk) - tн               Uоtн                   Uо

τ

• - U^ I ( t H ),                   (2)

где (т _о /U o ) I(t _K ) - ( t _o /U o ) I(t _H ) - абсолютное значение погрешности от краевых эффектов.

Погрешность от краевых эффектов неизбежна при реализации любых известных алгоритмов интегрирующего развертывающего преобразования с промежуточным преобразованием в сигнал импульсной модуляции. Например, существуют алгоритмы преобразования напряжения в ШИМ сигнал [1], которые в статике обеспечивают значение ∆ I = 0, однако в динамике ∆ I ≠ 0.

Описание алгоритма и схемной реализации

Предлагаемое техническое решение направлено на исключение погрешности от краевых эффектов с использованием способа [2], обеспечивающего упрощение алгоритма и схемной реализации ИАЦП. Суть способа заключается в следующем. Идеальное уравнение преобразование ИАЦП имеет вид:

J g o ( t ) U o dt = 0 , t - T c

• ¹    f 1    ¹

gxuxdt--

RxC t-∫Tc x x     RoC где Rx и Ro – резистивные сопротивления, через которые на вход интегратора ИАЦП подаются соответственно входное ux и опорное Uo напряжения; C – емкость конденсатора, используемого в интеграторе; Tc – длительность полного цикла преобразования; gx – весовая функция преобразуемого напряжения, в простейшем случае (как у нас) gx = 1; go – весовая функция опорного напряжения (на интервалах, где опорное напряжение отключено, go = 0, в остальных случаях ее значение равно +1 или –1, в зависимости от полярности опорного напряжения в соответствующие моменты времени).

С учетом методической погрешности от краевых эффектов уравнение преобразования, очевидно, имеет вид:

1 г g u dt

RC ^xx x t - T _c

^^^^^^^е

1 ^t

— J g o ( t ) U o dt = A I , (3)

RoC t-Tc где ∆I – разность значений выходной величины интегратора в начале и в конце цикла преобразования.

Обозначим через Ux среднее за полный цикл значение входного напряжения. Тогда для результата преобразования из (3) получим j go (t^dlt = RoUxxTc + ^RoC AI .

t - T _c             ^R x ^U o      ^U o

Таким образом, для исключения погрешности от краевых эффектов для всех известных способов интегрирующего аналого-цифрового преобразования с промежуточным преобразованием в один из сигналов импульсной модуляции достаточно к результату преобразования прибавить поправку, выражаемую вторым слагаемым правой части формулы (4), со знаком, противоположным знаку разности ∆ I .

На рис. 2 а представлена функциональная схема интегрирующего АЦП, реализующего рассматриваемый способ компенсации погрешности от краевых эффектов. Схема отличается от обоб- щенной схемы ИАЦП (см. рис. 1а) тем, что в нее введены два дополнительных функциональных блока: АЦП – малоразрядный АЦП и БВП – блок ввода поправок.

Для обеспечения компенсации погрешности от краевых эффектов в конце каждого полного цикла преобразования по команде с устройства управления малоразрядный АЦП преобразует выходную величину интегратора в цифровой эквивалент. Полученный код передается в блок ввода поправки, где из текущего значения выходного кода АЦП вычитается предшествующее значение, разность кодов умножается на постоянный коэффициент и полученная таким образом поправка суммируется с основным результатом преобразования, полученным в предшествующем цикле преобразования. Заметим, что операцию умножения на постоянный коэффициент можно исключить соответствующим подбором коэффициента преобразования дополнительного АЦП. Важно также, что смещение нуля дополнительного АЦП практически не влияет на точность вычисления поправки, так как при вычислении поправки происходит вычитание двух последовательных выходных кодов дополнительного малоразрядного АЦП.

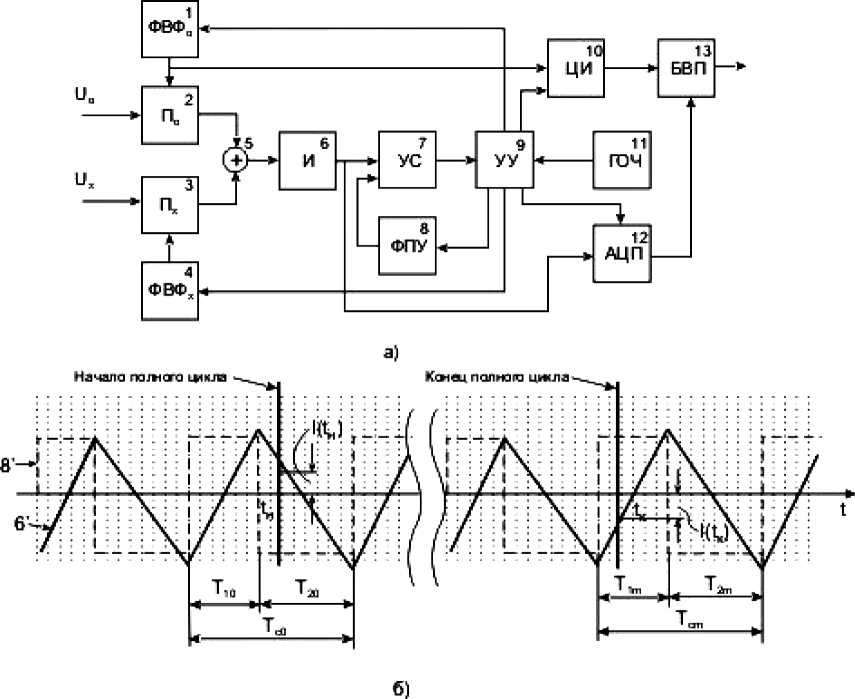
Рис. 2. Функциональная схема (а) и временные диаграммы работы (б) ИАЦП с компенсацией погрешности от краевых эффектов

Заключение

Приведенные в статье описание схемной реализации ИАЦП и алгоритма его работы позволяют обеспечить компенсацию одной из существенных составляющих методической погрешности интегрирующих преобразователей информации – погрешности от краевых эффектов.При этом по сравнению с аналогичными методами,реализуемыми,например,в ΣΔ -АЦП [3],достигается полная компенсация рассматриваемой составляющей погрешности преобразования более простыми техническими средствами.