Интеллектуальная робастная система управления одноколесным роботом-велосипедом на основе сквозных технологий мягких вычислений

INTELLIGENT ROBUST CONTROL SYSTEM OF ROBOTIC UNICYCLE BASED ON THE END-TO-END SOFT COMPUTING TECHNOLOGY

Ulyanov Sergey¹, Ulyanov Viktor ², Reshetnikov Andrey³, Tyatyushkina Olga⁴, Yamafuji Kazuo ⁵

1Doctor of Science in Physics and Mathematics, professor;

Dubna State University,

Institute of system analysis and management,

141980, Dubna, Moscow reg., Universitetskaya str., 19;

INESYS LLC (EFKO GROUP);

• ²    PhD in robotics;

INESYS LLC (EFKO GROUP);

115035, Moscow, Russia, Ovchinnikovskaya naberezhnaya 20, Bld 1, Business Centre “Central City Tower”;

NUST MISIS IYS Lab.;

119049, Moscow, Leninskiy prospekt 4;

• ³    PhD in informatics, associate professor;

Dubna State University, Institute of system analysis and management;

141980, Dubna, Moscow reg., Universitetskaya str., 19;

INESYS LLC (EFKO GROUP);

• ⁴    PhD, associate professor;

Dubna State University, Institute of system analysis and management;

141980, Dubna, Moscow reg., Universitetskaya str., 19;

• ⁵    PhD, professor;

University of Electro-Communications, Dept. of Mechanical and Control Eng.;

1-5-1 Chofu, Chofugaoka ,182 Tokyo, Japan;

Введение: Интеллектуальная мехатроника как базис исследования новых видов движения нелинейных механических систем и разработка современных методов и алгоритмов интеллектуального управления

Извлечение знания из новых видов движения основано на изучении «эталонных» (Benchmark) математических моделей. Движение одноколесного робота-велосипеда является одним из таких ви- дов движения (новая эталонная модель нелинейной механики [1-5]) , описанного как нелинейная, неголономная, глобальная неустойчивая динамическая система. Исследование таких динамических систем представляет огромный интерес в нелинейной механике (для разработки новых методов исследования нелинейных эффектов) и в современной теории управления (для разработки новых интеллектуальных алгоритмов управления).

Разработка алгоритма и системы управления в этом случае, для такого «эталона», как одноколесный велосипед, требует введения нового вида технологии вычислений - Интеллектуальные Вычисления. Физическая особенность одноколесного робота-велосипеда состоит в том, что управление реальным одноколесным велосипедом осуществляется опытным человеком-оператором. Это приводит к исследованию одноколесного велосипеда как биомеханической системы, включающей в себя новые подходы в системе управления, такие как интуиция, инстинкт и эмоции, присущие человеку-оператору и позволяет изучать возможность когнитивного управления за счет включения в контур управления «человеческого фактора». Управление движением одноколесным роботом-велосипедом основано на координации составляющих сложного движения (педалирование и движение туловища оператора). Изменение типа координации составляющих порождает новые типы движения (прямолинейное движения, слалом, танец, прыжки и т. д.).

Смежные работы . Предыдущие исследования, проведенные в области управления разными моделями системы одноколесного робота-велосипеда (см. таб. 1), рассматривали систему только с точки зрения механической модели с применением классических методов управления и/или упрощенного, смешанного нечеткого пропорционально - дифференциального регулятора (НПД) с эмпирическими таблицами нечетких решающих правил (ТНРП) [1-4]. Однако это стало алгоритмически неразрешимой проблемой для традиционных методов управления в задаче робастного устойчивого движения объекта и привело к появлению новых подходов для решения данной задачи.

Таблица 1. Другие модели одноколесного робота-велосипеда разных лет

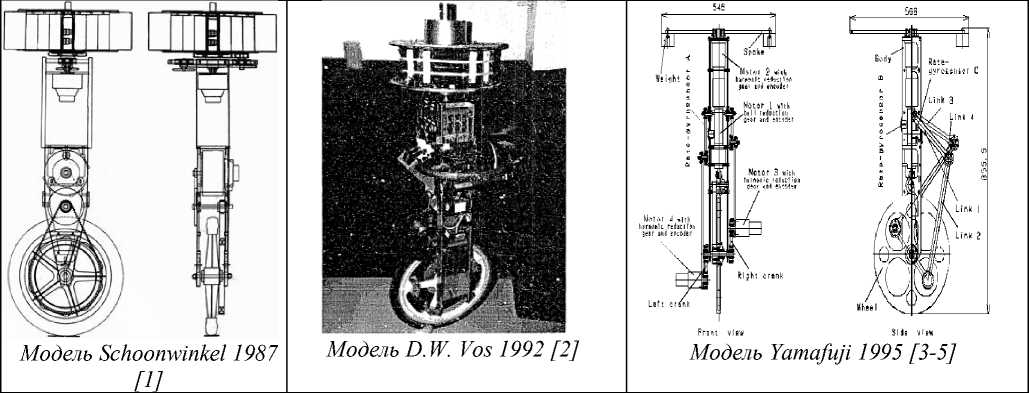
Модель Kim et all 2010

Модель Murata Seiko Girl 2011 [15]

Модель Eric Wieser

2018 [17]

Концепцией нашего исследования и разработки интеллектуальной системы управления одноколесным роботом-велосипедом стала структура, представленная на рис. 1.

Для решения задачи управления данным объектом была разработана и предложена киберфизиче-ская модель «Концептуальная Логическая Структура Распределенного Представления Знания (Информационные Уровни) в Искусственной Жизни Одноколесного Робота-Велосипеда» (рис. 1 а, б) как биомеханической модели движения и управления.

Основной задачей исследования является проблема изучения управления нелинейной биомеханической моделью одноколесного робота-велосипеда, а также создание и «обучение» системы управления посредством доступных методов и алгоритмов мягких вычислений.

Для оценки качества управления применялся новый физический принцип: минимум производства энтропии в движении системы и в системе управления [2-5, 7-13]. Физическая мера энтропии является функцией пригодности в генетическом алгоритме (ГА). Такой подход гарантирует глобальную устойчивость динамического объекта управления и обеспечивает робастность системы управления. На основе этого подхода была разработана “Самоорганизующаяся структура искусственной, интеллектуальной, робастной системы управления с новым физическим критерием качества управления” (см. ниже рис. 3) с новым видом интеллектуальной обратной связи, основанная на принципах интеллектуальных вычислении, а так же «Структура нечёткого моделирования интеллектуальной системы управления с алгоритмами мягких вычислений» (рис. 5).

В предыдущих исследованиях не была принята во внимание проблема внешних и внутренних воздействий на механическую систему и систему управления [1-4]. В результате это не дало глобальную динамическую устойчивость в управления объектом.

В данной работе представлена разработанная система моделирования и оптимизации интеллектуальной системы управления со стохастическим моделированием внешних/внутренних воздействий в механической системе и систем управления (неровности пола, механические колебания, уход нуля сенсоров и т. д.) с применением структуры формирующих фильтров [5].

Результаты моделирования и эксперимента подтверждают работоспособность системы управления моделью одноколесного робота-велосипеда.

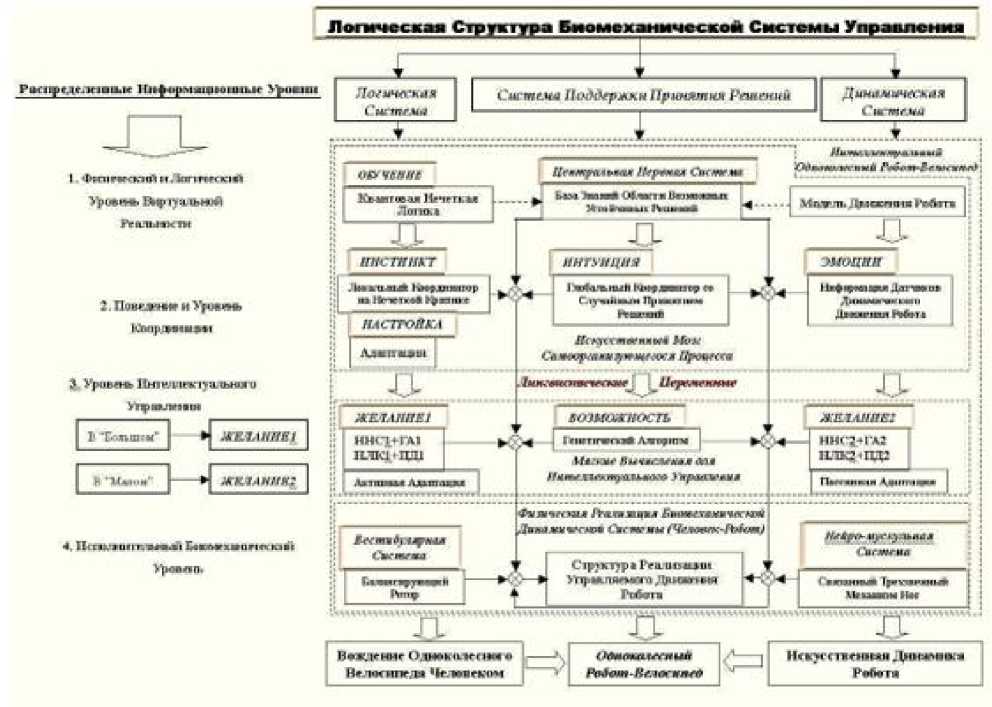
Рис. 1 (а). Концептуальная логическая структура распределенного представления знаний (информационные уровни) в искусственной жизни одноколесного робота-велосипеда

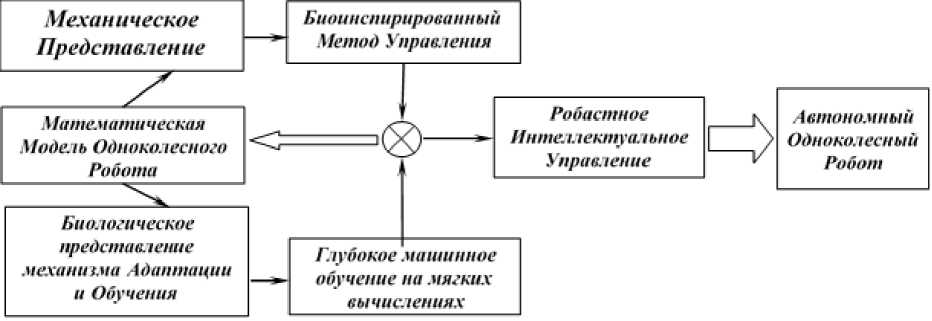
Рис. 1(б). Концепция исследования и разработки одноколесного робота-велосипеда

Постановка задачи и цель исследования: создание модели одноколесного робота-велосипеда с существенно нелинейными перекрестными связями между обобщенными координатами

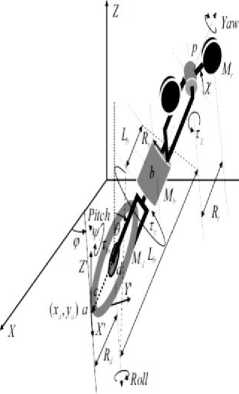
Как было сказано ранее, задачей данного исследования являлось создание интеллектуальной системы управления, неголономной, существенно нелинейной, а также глобально неустойчивой в пространстве и с большим количеством ограничений на связи, модели одноколесного робота-велосипеда. Для этого была создана новая математическая модель робота на основе “Реальной” системы координат одноколесного робота-велосипеда рис. 2.

Для этой модели мы определили следующие системы базисных и обобщенных координат, обобщенных скоростей, ускорений и сил:

Базисные Координаты - q j ( t) = [х0,у0,а,у, (3,6w,4^/,61,62,63,64,t] ; где j = 1,...,12 V( t) = 6w(t) + ^(const), ^(const) - начальная угловая позиция педалей, рис. 2. (звено 5,6). Здесь и далее индексы ( i , j ) обозначают порядковые номера элементов в соответствующих векторах, матрицах и в уравнениях системы.

Неголономные ограничения (в случае не проскальзывания колеса):

dx0(t)       d6w(t)            dy0(t)       d6w(t)

(1.1)

—Г— = ^Rw ' at ' ^{cos( a(t))} at = ^Rw ' at  ' ^{sm( a(t));}

ut            ^t                 ^t            ^t где Rw - радиус колеса, ^.^12 — скорость вращения колеса, a(t) - угол рыскания. Координаты х0, у0

исключаются подстановкой (1.1) в кинематическую часть Лагранжиана.

Обобщенные координаты - q j (t) = [а,у,Р, 6w, 61,62,63,64,]], j= 1,^,9.

Принятые обозначения на рис. 2: а - Угол рыскания; у - Угол раскачки ; в - Угол падения; C.M. -центр масс; L 1,^,6 - звенья 1-6; 0 w, 1, . ..,4 - углы поворотов звеньев; v - нач. угол педалирования.

Таким образом, при решении Лагранжиана с приведенными выше уравнениями неголономных ограничений и включением в него уравнений механических голономных ограничений и внешних сил стохастических воздействий, получаем следующее обобщенное выражение стохастического уравнения движения системы одноколесного робота-велосипеда с управлением:

'^((д)-^) =

= TTt + CTt(q,A) + fTz(t) - (BTtJ(q,q) - qj(t) + GTt(q) + DTt(q))

^t.n^q)- ^n =

= MctJ(q) - q^t) + Bcij(q,q') - qj (t) + GcTt(q) + DcTi(q) - TCTt - ^cTi(t)

(о).

(b)

(1.2)

где - i, j = 1,...,m ; q j (t) - вектор обобщенных ускорений; q j (t) - вектор обобщенных скоростей. В системе уравнений (1.2), уравнение ( a ) - динамическое уравнение движения со стохастическими воздействиями для целой модели одноколесного велосипеда, а уравнение (b) - описание множителей Лангранжиана Л_п , где n = 1,...,z. Матрицы, вектора и отдельные члены уравнений (1.2) подробно описаны в соответствующем разделе работы.

Стохастическое воздействие возникает в случае, если fc ; (t) и f ; (t) ф 0 описываются через решение дифференциального уравнения формирующего фильтра, как гауссовский (в нашем случае) случайный процесс, с автокорреляционной функцией вида R(t ^ ) = о]: - ехр( — а ^ - |т ^ |). Это воздействие включено в уравнение движения только для некоторых обобщенных координат, и моделирует возможные неровности пола, заедание в шатунно-кривошипном механизме, и погрешности углового измерения ускорения (ошибка дрейфа нуля гироскопических сенсоров).

При этих условиях мы получаем стохастическое уравнение движения с параметрическими воздействиями. Все это, дает возможность моделировать поведение динамической управляемой системы более реалистично и определять реальные параметры интеллектуального контроллера для получения ошибки и оценки устойчивости управления. Стохастическое моделирование случайных процессов через формирующие фильтры подробно описано в [5].

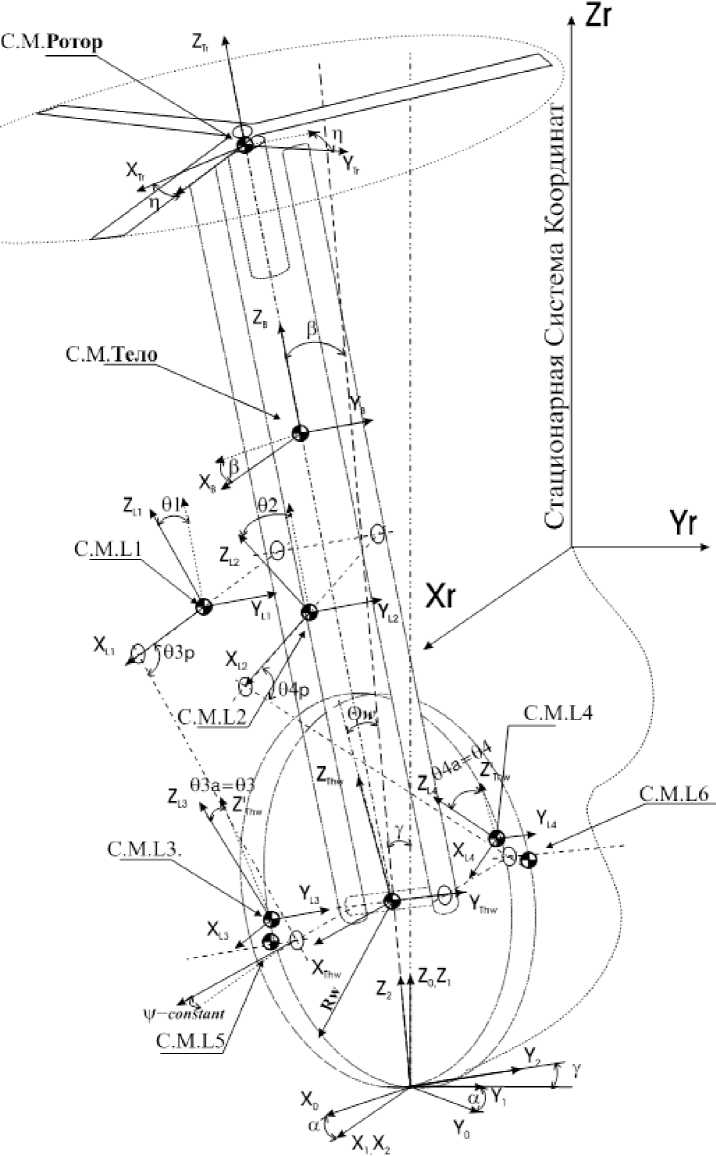
Рис. 2. Координатное описание модели одноколесного робота-велосипеда.

Оценка устойчивости динамической системы одноколесного робота-велосипеда

Для определения устойчивости мы используем теорему Сальвадори о равновесии механических систем с диссипативными силами вида Q i (q, q), с полной энергией динамической управляемой модели E(q,q), являющейся функцией Ляпунова V(q,q) = E(q,q) = T(q,q) + U(q); где T(q,q) есть кинетическая энергия системы, U (q) - потенциальная энергия системы. В соответствие с условиями теоремы Ляпунова, если функция V(q, q) удовлетворяет условиям :

• 1)    функция положительно определена относительно любых q, q и равна 0 при (q, q) = 0, то есть V(q,q) > ||d(q, q)|| и V(0,0) = 0, где а некоторая непрерывная, строго возрастающая функция, удовлетворяющая условию а (0,0) = 0;

• 2)    производная функции V(q, q) по времени t отрицательна, то есть V (q, q) < 0, то состояние системы изначально устойчиво [6].

Приведем также условия теоремы Сальвадори, определяющие устойчивость динамической системы. Допустим, что:

• 1)    U(q) имеет минимум в q = 0;

1a) U (q) не имеет минимум в q = 0;

• 2)    положение q = 0 является изолированным;

• 3)    абсолютное рассеивание (Qlq) < — |a(q)H, где а строго положительно определенная функция.

Тогда при выполнении условия 1) состояние равновесия (q, q) = 0 - устойчиво; в случае 2), при условии 1a), состояние равновесия (q,q) = 0 - неустойчиво.

Основываясь на обеих теоремах, мы в состоянии определить устойчивость системы одноколесного робота-велосипеда.

Уравнение потенциальной энергии системы одноколесного робота-велосипеда, для q j = (0,0,0,0, 61, 62, 63, 64, 0), имеет следующую форму:

^п(0)

= д •

[Sw^

М_п + М 3 • (2 • е1

— е2 • (sun( 61) + sin( 62))) + Az • М5

п                   п

• (cos( 63) + cos( 64)) + М₇ • е 6]

(1.3)

где 61,62, 63, 64 координаты, не равные 0 при углах y,P,6w = 0, есть механические голономные ограничения шатунно-кривошипного механизма; M i - массы частей одноколесного робота-велосипеда; el, e2, e6, Az - параметры частей робота. Из (1.3) следует, что U(0) имеет максимальное значение в положении равновесия. (1.3) удовлетворяет условию 1a) теоремы Сальвадори, что говорит о неустойчивости системы в положении равновесия. Это позволяет утверждение о глобально неустойчивости системы. Однако, как показано в [6], в том случае, когда U(0) имеет максимальное значение, возможно, что равновесие будет устойчиво вследствие приложения внешних гироскопических сил, что согласно нашему случаю, является управляемыми крутящими моментами.

Наше исследование показывает, что, возможно создать такую интеллектуальную систему управления, которая может стабилизировать динамическое движение глобально неустойчивой нелинейного объекта управления, что подтверждают результаты моделирования, представленные далее.

Методы решения задачи – Концептуальная Модель Управления Биомеханической Системой Одноколесного Робота-Велосипеда

Для обеспечения методов интеллектуальных вычислений, способных скоординировать составляющие сложного движения, необходимо применение качественно новых алгоритмов управления, способных оперировать с лингвистическими переменными [8]. Методы мягких вычислений полностью удовлетворяют этим требованиям, что и определяет их использование. Основываясь на физическом и интеллектуальном описании биомеханической модели, и используя методы мягких вычислений, мы представили следующую структуру моделирования системы интеллектуального управления.

Биомеханическая модель системы интеллектуального управления. Иерархический динамический процесс управления человеком одноколесным велосипедом может быть представлен следующими элементами:

• 1)    Динамическая система « человек-оператор - одноколесный велосипед» .

• 2)    Процесс принятия решений интеллектуальной системой управления с различными уровнями «умения вождения» .

• 3)    Логическое поведение координации человека (его туловища, рук и ног), основанное на механизмах интуиции, инстинкте и эмоциях.

• 4)    Распределенная информационная система для совместной координации подсистем в биомеханической модели [8].

В соответствии с этим представлением об интеллектуальном динамическом управлении, мы предлагаем концептуальную логическую структуру искусственной жизни одноколесного робота-велосипеда, как показано на рис. 1. Для описания искусственной жизни одноколесного робота-велосипеда мы используем методы качественной физики, описывающие внутреннее состояние виртуального мира робота, основанные на математической модели его движения.

Логическая структура биомеханической системы управления одноколесного велосипеда человеком включает четыре уровня:

• 1)    Распределенные информационные уровни с их подуровнями.

• 2)    Логическая система.

• 3)    Система поддержки принятия решений.

• 4)    Динамическая система.

Далее, мы подробно изложим основные положения данной структуры. Распределенные информационные уровни включают четыре подуровня:

• 1)    Физический и логический уровень виртуальной реальности;

• 2)    Поведение и уровень координации;

• 3)    Интеллектуальное управление с двумя подуровнями;

• 4)    Исполнительный биомеханический уровень.

Пересечения между горизонтальными линиями распределенных информационных уровней и вертикальными линиями логической системы, системы поддержки принятия решения, и динамической системы (движение одноколесного велосипеда и поведения человека, как биомеханическая модель управления) реализуют специфические для человека модели поездки на одноколесном велосипеде с различными уровнями умения использовать интеллектуальные средства управления. Рассмотрим здесь этот подход на примерах.

Пример 1: Физический и логический уровень виртуальной действительности . Пересечение первого горизонтального уровня (Физический и логический уровень виртуальной реальности) с первым вертикальным уровнем (Логическая система) дает в результате структуру процесса обучения человека управлению одноколесным велосипедом. Пересечение со вторым вертикальным уровнем (Система поддержки принятия решений) соответствует уровню центральной нервной системы, как биологической системе управления. Пересечение с третьим уровнем (Динамическая (механическая) система) представляет механическую модель движения одноколесного велосипеда, как динамической системы. Логическая сумма этих подуровней реализует физический уровень описания движения одноколесного велосипеда и физическую интерпретацию экспериментальных данных (попыток). Математической основой описания процесса обучения является квантовая нечёткая логика . Функции центральной нервной системы реализованы как область базы знаний (БЗ) возможных устойчивых решений. Но создать систему управления такого высокого интеллектуального уровня в настоящее время не представляется возможным.

Пример 2: Поведение и уровень координации . Эта структура включает механизмы инстинкта , интуиции и эмоции . Механизм инстинкта описан в логической структуре как локальный координатор с помощью нечётких правил и соответствует структуре управления с активной и пассивной адаптацией на основе нечёткой нейронной сети (ННС). Механизм интуиции представляется как глобальный координатор и реализован в процессе управления как процесс принятия решения на основе генетического алгоритма (ГА). Механизм эмоций описан на основании информации от датчиков движения и представлен в форме таблиц решающих правил с различным семантическим выражением лингвистического описания желательного динамического поведения движения (как примеры, «плавно», «быстро» и так далее). Таким образом, пересечения двух распределенных информационных уровней с логическими системами реализует блок искусственного мозга для процесса самоорганизации системы управления одноколёсным велосипедом.

Пример 3: Уровень Интеллектуального управления – интеллектуальная система управления с распределенным представлением знаний, включающая в себя понятия желания и возможности точно так же, как человек [9,10]. Для механизмов инстинкта и эмоции новые таблиц решающих правил определяются с помощью ННС. Механизм интуиции реализован на базе ГА и руководит действиями двух нечетких регуляторов. Таким образом, нечеткое моделирование, основанное на математических инструментальных средствах ГА и ННС, реализует алгоритм мягких вычислений в системе интеллектуального управления роботом.

Из качественного физического описания и математического моделирования движения мы получаем область возможных устойчивых решений, описанных, как это было показано в [3,4], странным аттрактором. Этот говорит о том, что человеческая система управления - высоко организованная, комплексная система и положение тела человека меняется стохастическим образом. Это полностью соответствует результатам, описанным в [11].

Пример 4: Исполнительный биомеханический уровень - физический процесс реализации системы одноколесного робота-велосипеда. В этом случае вестибулярная система, как логическая система управления, реализована балансирующим ротором (торс, плечевой пояс и руки), а нейро-мускульная система сформирована с помощью шатунно-кривошипного механизма ног.

Таким образом, динамический процесс управления человеком одноколесного велосипеда, с интеллектуально различными формами поведения, может быть описан как пересечение логических систем с распределенными информационными уровнями.

Структуризация интеллектуальной, робастной системы управления. Разработка робастного управления движением сложных динамических систем имеет два пути исследования: 1) изучение устойчивых процессов движения; и 2) изучение процессов неустойчивого движения сложных динамических систем.

Как было сказано выше, мы сконцентрировали наше внимание на изучении одноколесного робота-велосипеда, как динамического, глобально пространственно-неустойчивого управляемого объекта. Такой глобально пространственно-неустойчивый динамический объект требует нового интеллектуального робастного алгоритма управления, основанного на знании описания движения существенно нелинейной, неустойчивой динамической системы [3, 8]. Структура интеллектуального робастного алгоритма управления в концептуальной форме, для всего класса неустойчивых динамических объектов управления, была описана в [2-4, 8], здесь же мы применим ее в задаче управления одноколесным роботом-велосипедом.

Структура управления с новым видом интеллектуальной обратной связи, представлена на рис.3. Она основывается на классической схеме системы управления с линейной обратной связью П(И)Д, инструментарии интеллектуальных мягких вычислении (теория нечетких множеств, нечеткие нейронные сети (ННС), генетический алгоритмы (ГА)); нелинейной модели объекта управления; вычислении производства энтропии; стохастическом моделировании случайных внешних/внутренних воздействий.

В структуру мы используем следующие обозначения: f - функция пригодности ГА; S - энтропия системы; S c - энтропия контроллера (регулятора); S i - энтропия объекта управления (одноколесный робот-велосипед); e - ошибка управления; и * - оптимальный сигнал управления; m ( t ) - внеш-ние/внутренние воздействия; НР - нечеткий контроллер (регулятор); НЛСК - нечеткая логическая система классификации; СМКУ - система моделирования качества управления; K - оптимальные коэффициенты усиления регулятора (обучающий сигнал); ТНРП - таблица нечетких решающих правил; КУ - коэффициенты усиления регулятора (в случае 2-х ПД регуляторов K = ( k 1 , k 2 , k 3 , k 4 )).

Самоорганизация управления в данной системе, на первом этапе, обеспечивается путем оптимизации параметров управления П(И)Д контроллера посредством отбора наилучших решений генетическим алгоритмом, критерием отбора в котором служит наилучшая пригодность решения, вычисляемая с помощью функции пригодности. Для определения пригодности используется новая физическая мера качества управления - минимум производства энтропии . Данная мера является разностью между производством энтропии самим объектом управления и включенной в него системы управления. Это позволяет адаптировать параметры линейной системы управления к нелинейному объекту управления [7, 12].

Следующим этапом адаптации является обучение системы управления для обеспечения ее робастности. Данный этап основан на нечетком логическом классификаторе, который определяет нечеткие правила логических соотношений параметров линейного контроллера. Классификатором служит ННС, обучающим сигналом, для которой являются оптимизированные параметра управления полученные с выхода генетического алгоритма. Данный этап формирует таблицы нечетких решающих правил, адаптированных параметров управления котроллера низкого уровня П(И)Д.

В этом подходе, решения проблемы управления нелинейным объектом, критерием качества управления (управляемости) играет функция вычисление производства энтропии, которая, как было показано в [7, 12, 13], напрямую связана с функцией Ляпунова, т.е. динамической устойчивостью системы. Взаимосвязь этих функций в интеллектуальной системе управления обеспечивает ее робастность, как показано на рис.4. Далее, полученные таблицы решающих правил используются нечетким контроллером (НК) для управления параметрами линейного контроллера.

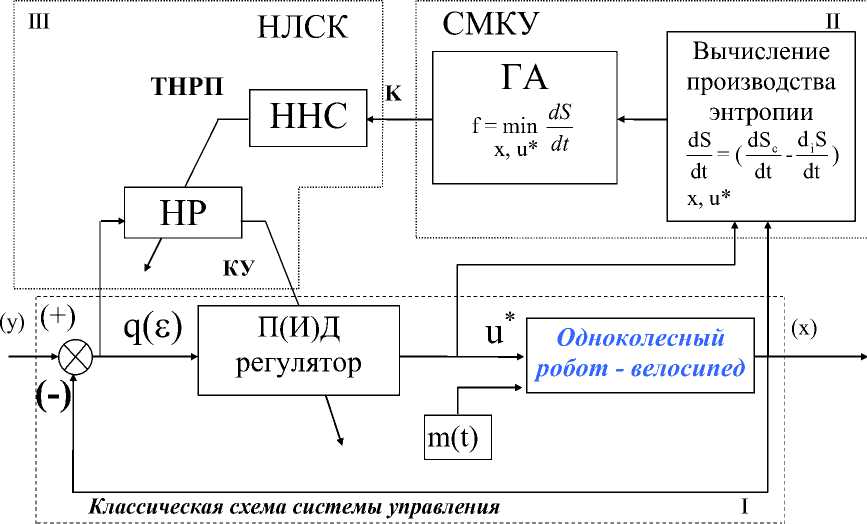
Рис. 3. Самоорганизующаяся Структура Искусственной, Интеллектуальной, Робастной Системы Управления с Новым Физическим Критерием Качества Управления

Устойчивость

Функция Ляпунова

Робастность

Интеллектуальная система управления

Управляемость

Минимум производства энтропии j

Рис. 4. Структура взаимосвязи Устойчивости, Робастности и Управляемости системы

Основываясь на структуре интеллектуального управления и взаимосвязи на рис. 4, была разработана Структура Нечёткого Моделирования Интеллектуальной Системы Управления, представленная на рис.5.

Моделирование разбито на два основных этапа: Н еавтономное и А втономное. На первом этапе происходит создание математической модели управляемого объекта и нахождение термодинамических уравнений его состояния для просчета энтропии. Далее уравнения нахождения энтропии формируют функцию принадлежности ГА. ГА в режиме компьютерного стохастического моделирования оптимизирует параметры П(И)Д контроллера. Следующим этапом является обучение системы управ- ления, на основе полученных от ГА оптимизированных параметров контроллера, и получение таблиц решающих правил (Базы знаний НК) с применением ННС.

В On-line режиме на основе полученных таблиц решающих правил нечетким контроллером осуществляется изменение параметров П(И)Д регулятора модели одноколесного робота-велосипеда, в реальном масштабе времени. Структура системы управления моделью робота описана далее.

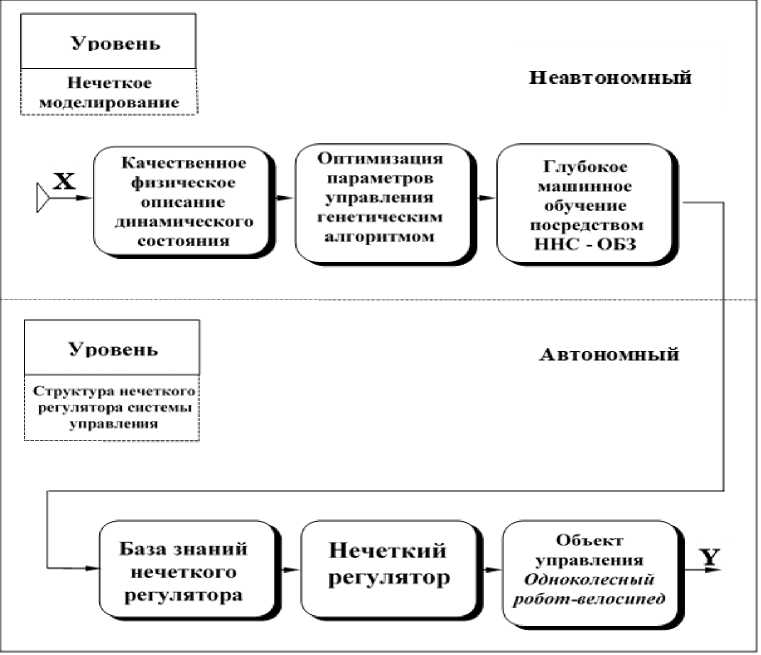
Рис. 5. Структура Нечёткого Моделирования Интеллектуальной Системы Управления

Математическое моделирование системы с применением методов мягких вычислений.

Основой моделирования является математическое описание движения объекта управления, представленное (1.2). Остановимся подробнее на описании уравнений (1.2).

Для математического моделирования движения одноколесного робота-велосипеда мы приняли следующие параметры модели (1.2), графически представленной на рис. 2:

ij = 1 ... 9; q j (t~) = [а, у, Р, 6w, 61, 62,63,64, q] - вектор обобщенных ускорений;

q j (t) = [а, у, Р, 6w, 61, 62,63, 64, Т] — вектор обобщенных скоростей; множители Лангранжа Л_п, где n = 1 ... 4.

В (1.2), (a), ME i,j (q) - 9 х 9 блок-матрица состоящая из множителей инерциальных ускорений М(q) , полученных из уравнений Лагранжа и множителей геометрических ускорений E(q) , полученных из уравнений механических ограничений шатунно-кривошипного механизма; BT ц (q, q) - 9 х 9 блок-матрица, состоящая из множителей кориолисовых и центробежных частей уравнения B(q, q) и T(q, q) , полученных из уравнений Лагранжа и уравнений шатунно-кривошипного механизма, соответственно;      G i (q)     —     9-мерный     вектор     гравитационных     множителей;

^i(q) = [0, G2(q), G3(q), G4(q),0,0,0,0,0]; Di(q,q) - 9-мерный вектор сил вязкого трения D^q) = [D1(q),D2(q),D3(q),D4(q),0,0,0,0,D9(q)]; Т; - 9-мерный вектор моментов вращения управляющих приводов: Т; = [0,0,0,0,0,0,0,0,7(^)3]; C;(q,Л) - 9-мерный вектор множителей Лагранжа с соответ- ствующими    коэффициентами    уравнений    голономных ограничений     C;(q, Л) =

[0,0, C (p) _i, C (9 _W ) ₂, 0,0,0,0,0]; f ; (t) - 9-мерный вектор случайных стохастических воздействий.

	- Mn(q)  ..     ..	■■      ■■      M 19 (q)-
ME;,^ =	..         ..         .. M4 i (^)  ..     .. 0     0  E53(q)	■■         ■■              ■■ ■ ■      ■■      M 49 (q) ■■  E5 8 (q)      0	;
" B i	..         ..         .. 0     0   E 83 (q) LM gi (q)   ..     .. i (q,q>)   ■■         ■■	■ ■          ■■               0 ■■   E83(q)      0 ■ ■      ■■      M99(q). ■ ■         ■■         B19(t	i ,q)
..           ..          .. B 4i (q,q)   ■ ■        ■ ■		■■          ■■                 ■■ ■■       ■■        B49(q, q^
BTiJ(q,q)=    0     0  r 53 (q,q) V     " „ 7 , 0    0     qq _B 9i (q,q')   ..        ..		■■   T 58 (_q,q)        0 ■ ■            ■■                   0 ■ ■   E8s (q,q)       0 ■ ■        ■■        B99(q,q).

В (1.2), ( b ), Mc i,j (q) - 9 х 9 матрица множителей инерционных ускорений M(q), полученных из уравнения Лагранжа; Bc , (q, q) - 9 х 9 матрица множителей кариолисовых и центробежных частей уравнения B(q, q) , полученные из уравнения Лагранжа; Gc(q) - 9-мерный вектор гравитационных Gc ; (q) = [0,0,0,0, G₅(q), G₆(q), G₇(q), G₈(q),0] множителей; Dc(q,q) - 9-мерный вектор сил вязкого трения DC i (q) = [0,0,0,0, D 5 (q), D₆(q), D₇(q), D₈(q),0]; tC ; - 9-мерный вектор моментов вращения tC ; = [0,0,0,0,0,0, t (9 ₃ ) ₁,t (94)2 , 0] управляющих приводов; fc ; (t) - 9-мерный вектор случайных стохастических воздействий; A i,n (q) - 9 х 4 матрица геометрических множителей, полученных из уравнений механических ограничений шатунно-кривошипного механизма, соответствующая уравнению движения через i-й индекс; Л_п - 4-мерный вектор множителей Лагранжа:

	1 0	■■       0		0            ■ ■	0     1
MCij(q) =	M gi (q) ■■	■■         ■■ ■■ M5 9 (q) ■■         ■■	;BC ij (q,q) =	■■           ■■ B5 i (q,q)  ■■ ■■           ■■	■■ B5 9 (q,q) ■■
	M 8i (q)	■■   M89(q)		B 81 (q,q^  ■■	B 89 (q,q)
	L   0	■■        0     .		L     0         ■■	0.
		0	000

	^ si (q)	^ 52(q)	0	0
A ;,n (q) =	0	0	^ es (q)	^ 64 (q)
	^ 7i (q)	^ 72(q)	0	0
	0	0	^ 83(q)	^ 84 (q)
	L    0	0	0	0.

У равнения управления крутящими моментами в системе одноколесного робота-велосипеда. В случае ПД контроллера для шатунно-кривошипного механизма, управляемые крутящие моменты представляются следующим образом:

Т ( _УЗ )1 = —^ 4)2 = -kp1(T) ■ P(t) - kd1(T) ■ P(t), (4.1)

а для механизма ротора:

т_№ з = kp2(T) ■ y(t) + kd2(T) ■ y(t).

(4.2)

В общей схеме моделирования ГА оптимизирует и генерирует параметры ПД контроллера kp1(T), kp2(T), kd1(T), kd2(T), выбирая их на основе результатов вычислений по функции пригодности, как это будет показано далее с дискретностью T = 0.05 сек. Время периодичности обновления определено из реальной схемы управления одноколесного робота-велосипеда.

Информационно-термодинамический критерий распределения качеств управления. Термодинамическое соотношение качества робастного интеллектуального управления, и критерий оптимизации, используемый в квантовом алгоритме (КА) самоорганизации баз знаний (БЗ) [1], приведено в табл. 2.

Табл. 2. Термодинамический критерий распределения качества робастного управления

В табл. 2 введены следующие обозначения: V - функция Ляпунова; S oy , S p — производство энтропии в ОУ и регуляторе, соответственно; V =-У ^_1 q² + - S²; S = S oy — S p ; q j = ф(q j ,u, t) -уравнение движения ОУ; q ^ - обобщенная координата; и - искомое управление.

В табл. 2 уравнение распределения качеств управления динамической системы связывает в аналитической форме на основе понятия энтропии феноменологической термодинамики такие качественные понятия теории управления как устойчивость , управляемость и робастность . В результате необходимое распределение между уровнями устойчивости, управляемости и робастностью, позволяет достигать цели управления в нештатных ситуациях с минимальным расходом полезного ресурса за счет применения в качестве функции пригодности в генетическом алгоритме критерия минимума производства обобщенной энтропии. Термодинамическое определение S и информационной H энтропии связаны соотношением фон Неймана в виде: S = кН = —к ^ р ; Inp j , где к« 1.38 X 10^-23 Дж /К и является постоянной Больцмана. В результате (после подстановки данного соотношения) получим уравнение, которое связывает также устойчивость, управляемость и робастность, но уже на основе информационной энтропии Шеннона, позволяющее определять управление для гарантированного достижения цели управления в нештатных ситуациях уже с требованием минимального количества информации о внешней среде и о состоянии ОУ.

Следовательно, данные соотношения составляют систему уравнений, определяющее управление, которое гарантирует достижение цели управления в нештатных ситуациях с минимальным расходом полезного ресурса и минимально требуемой исходной информации [1-4].

Информационно-термодинамическое распределение мер качества управления. Допустим, что объект управления описывается в общем виде уравнением q ^ = ^(q, t, S(t),u), где обобщенная координата q j описывает движение объекта управления, и представляет управление и S(t) = S_O y (t) — S p (t) представляет обобщенную энтропию системы как разность между производством энтропии объектом управления S_O y (t) и производством энтропии S p (t) регулятором. Рассмотрим уравнение следующего вида:

=Z r=i q i -^(q,t,S(t),u) + (S oy —S p )-(S oy —S p )<0.        (4.3)

^

устойчивость          управляемость                  робастность

Уравнение (4.3) связывает в аналитической форме такие качественные понятия теории управления как устойчивость V (функция Ляпунова), управляемость и робастность на основе понятия энтропии феноменологической термодинамики [1-6].

Такой подход позволяет, как отмечалось ранее, найти необходимое распределение между уровнями устойчивости, управляемости и робастностью, позволяющее достигать цели управления в нештатных ситуациях с минимальным расходом полезного ресурса за счет применения в качестве функции пригодности в генетическом алгоритме минимум производства обобщенной энтропии, входящей в правую часть (4.3).

Рассмотрим теперь (4.3) с учетом связи термодинамической энтропии с информационной энтропией Шеннона. Термодинамическое определение S и информационной H энтропий связаны соотношением фон Неймана^1,2 в виде: 5 = кН = -k^P i Inp i , где к « 1.38 X 10^-23дж/К и является постоянной Больцмана. Подставим в уравнение (4.3) вместо 5(t) информационную энтропию Шеннона - H . В результате получим:

^ =^?=1Qi-v(q,t,k(Hоу -Нр),и) + к(Ноу -Нр)*(НОу -Нр)<0. (4.4) ХУ устойчивость управляемость робастность

Таким образом, уравнение (4.4) связывает также устойчивость, управляемость и робастность, но уже на основе информационной энтропии Шеннона, позволяющее также определять управление для гарантированного достижения цели управления в нештатных ситуациях с требованием минимального количества информации о внешней среде и о состоянии объекта управления. Следовательно (4.3) и (4.4) составляют систему уравнений, решение которой определяет управление, гарантирующее достижение цели управления в нештатных ситуациях с минимальным расходом полезного ресурса и минимально требуемой исходной информации.

Информационно-термодинамический анализ когнитивной интеллектуальной системы управления

Обобщением уравнений (4.3) и (4.4) является следующая система уравнений:

dy dt стойчивость

d7 dt устойчивость

^ i=1 ^q i * ^{ф (q},^t, ^k ( ⁵оу

-

⁽⁵Тр + ⁵Кр⁾ ), ^м ) ⁺

управляемость

⁺ ( ⁵оу ^{- (5}Тр ⁺ ^ Кр )) * ( ⁵оу ^{- (5}Тр + ^ Кр )) < 0,

(5.1)

робастность

= Е ”=1 ^q i * ^{ф (q,t,k (Н} оу ^{- (Н} Тр + ^Н Кр )) ^,и) + (^Н оу ^{- (Н} Тр + ^Н Кр )) * (^Н оу ^{- (Н} Тр + ^Н Кр )) < ⁰,     ^(5.2)

управляемость

робастность

где ( ⁵Тр ^{+ 5}Кр ) и (Н Тр + Н Кр ) означают суммарные термодинамические и информационные энтропии технического и когнитивного регуляторов соответственно.

Из уравнения (5.1) следует, что робастность интеллектуальной системы управления возможно повысить за счет производства энтропии когнитивного регулятора, который уменьшает потери полезного ресурса, а уравнение (5.2) показывает, что негэнтропия когнитивного регулятора снижает требования к минимуму исходной информации для достижения робастности. При этом информация, основанная на знаниях в БЗ когнитивного регулятора, позволяет получить дополнительный ресурс для полезной работы, что эквивалентно появлению целенаправленного действия на объект управления для гарантированного достижения цели управления.

Одной из ключевых задач современной робототехнике является развитие технологий когнитивного взаимодействия робототехнических систем, позволяющие решать задачи интеллектуального иерархического управления за счет перераспределения знаний и функций управления, например, традиционно между лидером и подчиненным (“master – slave” system). Современные подходы к решению данной задачи основываются на теории многоагентных систем, теории роевого искусственного интеллекта и мн. др. [1-8].

В многоагентной системе существует, согласно [9-12], новый синергетический информационный эффект самоорганизации баз знаний и формирования дополнительного информационного ресурса, возникающий при обмене информацией и знаниями между активными агентами (swarm synergetic information effect). Извлечение дополнительного ресурса в виде скрытой в классических состояниях квантовой информации осуществляется на основе квантового нечеткого вывода, который, в свою очередь, является новым квантовым поисковым алгоритмом и частным случаем квантового алгоритма самоорганизации.

За счет синергетического эффекта создается дополнительный информационный ресурс и многоагентная система способна решать сложные динамические задачи по выполнению совместной работы. Поставленная задача может не выполняться каждым элементом (агентом) системы в отдельности в разнообразных средах без внешнего управления, контроля или координации, но обмен знаниями и информацией позволяет совершать совместную полезную работу для достижения поставленной цели управления в условиях неопределенности исходной информации и ограничений на расход полезного ресурса [10]. В частности, известно, что для систем управления с обратной связью, количество извлекаемой полезной работы W удовлетворяет неравенству W_max( t) = к J Т_т i _nI dt ' <  кТ I _с, где к - постоянная Больцмана, T_min(_t) интерпретируется как наименьшая достижимая температура системой во времени t при управлении с обратной связью, предполагая Т_т ^ _л(0) = Т, и 1_с определяет количество информации Шеннона (перенос энтропии), извлекаемое системой из процесса измерения [13,14].

Физически синергетический эффект означает самоорганизацию знаний и создание дополнительного количества информации, которая позволяет совершить многоагентной системе максимально полезную работу с минимумом потери полезного ресурса и при минимуме требуемой исходной информации, без разрушения нижнего исполнительного уровня системы управления [11,12,14]. Совместно с информационно-термодинамическим законом интеллектуального управления (оптимальное распределение качеств управления «устойчивость – управляемость – робастность») проектируется интеллектуальная система управления (ИСУ) многоагентными системами, гарантирующая достижение цели управления в условиях неопределенности исходной информации и ограниченного полезного ресурса [10-12,14].

Рассмотрим подробнее данные утверждения на основе анализа взаимоотношений между количеством информации и извлекаемой на ее основе полезной работы и свободной энергии.

Как отмечалось выше, если наблюдателю в виде демона Максвелла доступны микроскопические степени свободы, то второй закон термодинамики может быть нарушен. Сцилард показал из анализа модели демона Максвелла, что из термодинамического цикла извлекается работа в виде кТ In 2. Более того³, было показано, что извлекаемая работа W^ из системы определяется количеством информации (или квантово-классической взаимной информацией) I, которая измеряет знания о системе при измерении. Одновременно подобное соотношение в виде нижней границы существует для полной стоимости W_c ^ _st измерения и стирания информации W_e ^. _t < -ДР⁵ + кТ1 и W_c ^ _st >  кТ1, где ДР⁵ определяет свободную энергию системы. Тогда нетрудно заметить, скорость извлекаемой работы W_ext ограничена величиной W_ext< кТ1, т. е. ограничена скоростью извлекаемой информации⁴.

Предложена модель КА самоорганизации ИСУ, базирующаяся на принципах минимума информационной энтропии (в «интеллектуальном» состоянии сигналов управления) и обобщенной термодинамической мере производства энтропии (в системе «объект управления + регулятор»). Основным результатом применения процесса самоорганизации является приобретение необходимого уровня робастности и свойства гибкости (адаптивности) воспроизводимой структуры. Отмечено, что свой- ство робастности (по своей физической природе) выступает составной частью самоорганизации, а требуемый уровень робастности ИСУ достигается за счет выполнения отмеченного выше принципа минимума производства обобщенной энтропии. Принцип минимума производства энтропии в ОУ и системе управления [7] служит физическим принципом оптимального функционирования с минимальным расходом полезной работы и лежит в основе разработки робастной ИСУ. Данное утверждение базируется на том, что для общего случая управления динамическими объектами оптимальное решение конечной вариационной проблемы определения максимума полезной работы W эквивалентно, согласно [8], решению конечной вариационной проблемы нахождения минимума производства энтропии S. Таким образом, исследование условия максимума функционала max(W) (где - обоб-qi,n щенные координаты ОУ и сигнал управления соответственно) эквивалентно, согласно [7, 9], исследованию ассоциированной проблемы минимума производства энтропии, т.е. mln(S). Следовательно, в

Q l ,^

разработанной модели КА используемый принцип минимума информационной энтропии гарантирует необходимое условие самоорганизации – минимум требуемой исходной информации в сигналах обучения; термодинамический критерий минимума новой меры обобщенного производства энтропии обеспечивает достаточное условие самоорганизации – робастность процессов управления с минимальным расходом полезного ресурса.

Более значимым является факт, что усредненная величина произведенной работы силами диссипации ^^S⁸ = S_KL(P_F^P_B), т. е. работа сил диссипации определяется дивергенцией Кульбака-Лейблера для вероятностных распределений P_F,P_B • Отметим, что левая часть данного соотношения представляет физически тепловую энергию, а правая часть определяет чисто информацию о системе.

Информационная энтропия является мерой количества информации о системе и расхождения Кульбака – Лейблера, а также определения количества информации Фишера.

Аналогичная зависимость существует между работой, произведенной силами диссипации, и расхождением Реньи [30].

Таким образом, подставляя в (5.1) и (5.2) приведенные соотношения между информацией и извлекаемой свободной энергии и работы получаем отмеченный выше вывод, что робастность интеллектуальной системы управления возможно повысить за счет производства энтропии когнитивного регулятора, который уменьшает потери полезного ресурса объекта управления, а негэнтропия когнитивного регулятора снижает требования к минимуму исходной информации для достижения робастности. Поэтому извлекаемая информация, основанная на знаниях в БЗ когнитивного регулятора, позволяет получить дополнительный ресурс для полезной работы, что эквивалентно появлению целенаправленного действия на объект управления для гарантированного достижения цели управления.

Общая структура математического моделирования. Структура Нечёткого Моделирования Интеллектуальной Системы Управления, представленная на рис.5, как это сказано ранее, разбито на два основных этапа: автономный и неавтономный .

В неавтономном режиме происходит создание математической модели управляемого объекта, нахождение термодинамических уравнений его состояния для просчета энтропии, формирующие функцию пригодности ГА, стохастическое математическое моделирование с ГА оптимизирующего параметры П(И)Д контроллера.

ГА случайным образом выбирает оптимальные значения параметров управления ПД контроллера в области всех возможных решений, используя в качестве критерия пригодности решения (функции пригодности) минимум производства энтропии в самой интеллектуальной системе управления и в динамическом поведении сложной нелинейной модели. Функция пригодности ГА представлена как:

Eval = mln( (Sp - Sc)(_^ — dS^)), 4 4             dt     dt y, dsp

(5.3)

dsc

где – скорость производства энтропии системы управления; – скорость производства энтропии динамической управляемой модели одноколесного робота-велосипеда, со следующим условием: ^d S- >  ^7- . Подробно определение вычисления энтропии представлено в [7].

Термодинамическое уравнение движения. Уравнения вычисления производства энтропии для интеллектуальной системы управления и динамического поведения управляемой модели получены из теоретического подхода, представленного в [7], и для одноколесного робота-велосипеда имеют следующий вид:

■as y dt ds^c

. dt -

Mi=/(q) 0

■4

^ i=y (q, q) • q^T(t) + D^T(q)

tT

^] • ^{q T (t)} .

(5.4)

Здесь i, j = 1 ... 9; M i=j (q) - 9 x 9 диагональная матрица множителей инерционных ускорений M(q), полученных из решения уравнения Лагранжа; B i=j (q, q) - 9 x 9 диагональная матрица множителей Кориолисовых и центробежных частей уравнения, полученных из решения уравнения Лагранжа; D(q)        -        9-мерный        вектор        множителей        сил         D ^ (q) =

[D₁(q),D 2 (q),D 3 (q),D 4 (q),D 5 (q-),D₆(q),D 7 (q),D₈(q),D 9 (q-)] вязкого трения; T d — 9-мерный вектор диссипативных частей уравнений управления моментами вращения: kd i • [^,У’], T d = [0,Т з ,Т 1,2 ,0,0,0,0,0,0].

Следуя схеме рис. 5, следующим этапом является обучение системы управления на основе полученных от ГА оптимизированных параметров контроллера и получение таблиц решающих правил (Базы знаний НК) с применением ННС.

В автономном режиме на основе полученных таблиц решающих правил нечетким контроллером осуществляется изменение параметров П(И)Д регулятора модели одноколесного робота-велосипеда, в реальном масштабе времени.

Результаты математического моделирования и эксперимента

Структура нечеткого моделирования на схеме 1 в системе MathLab/Simulink состоит из следующих блоков:

• 1.    Блок основных уравнений;

• 2.    Блок произвольного возбуждения;

• 3.    Блоки коэффициентов уравнения;

• 4.    Блоки вычисления множителей Лагранжа;

• 5.    Блок интеллектуальной системы управления, основанной на ГА или ННС.

Во всех случаях, для моделирования использовались реальные параметры модели одноколесного робота-велосипеда рис. 6, а также соответствующие стохастические воздействия: от пола на угол вращения и в шатунно-кривошипном механизме (см. рис. 7).

Для ускорения процессов моделирования был применён метод исключения алгебраических петель, подробно описанный в патенте [18]. Данный метод позволил ускорить процесс компьютерного моделирования, а именно, время интегрирования примерно в 190!! раз, при изменении результата интегрирования менее чем на 1%, как это представлено на рис. 8 и рис. 9.

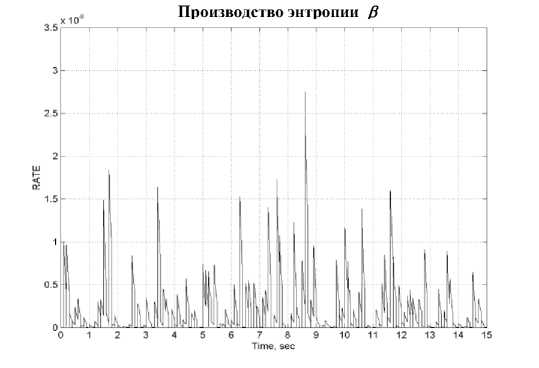
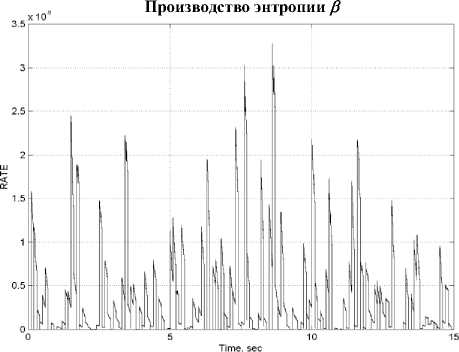
Обсуждение результатов моделирования. На рис. 10 показано сравнение трех типов подходов к управлению:

• a)    С классическим ПД контроллером и фиксированными коэффициентами усиления - временное изменение механического и термодинамического поведения системы;

• b)    С ГА-ПД контроллером и функцией пригодности – минимум производства энтропии;

• c)    С нечетким ПД контроллером и найденными для него таблицами решающих правил, полученными после процесса обучения на ННС.

Структура такого вида наиболее применима из-за ее гибкости, и мы имеем возможность изменять только необходимые блоки - управления, основных уравнений, случайных воздействий и т.д., без изменения структуры в целом.

Из результатов моделирования очевидно, что: 1) использование подхода, описанного выше, с применением минимума производства энтропии, как функции пригодности ГА процесса обучения

ННС, полностью справедливо; 2) динамическое движение происходит более гладко даже при дискретизации сигнала управления с периодичностью обновления сигнала = 0.05 сек.

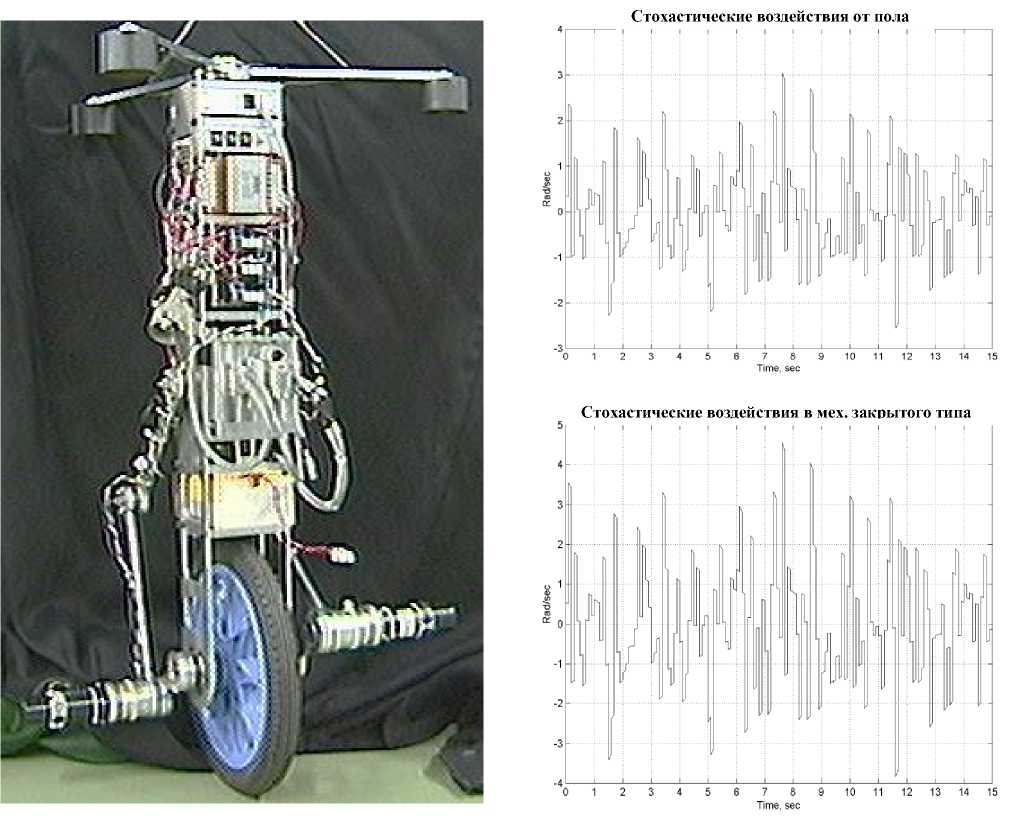
Рис. 6. Одноколесный робот-велосипед

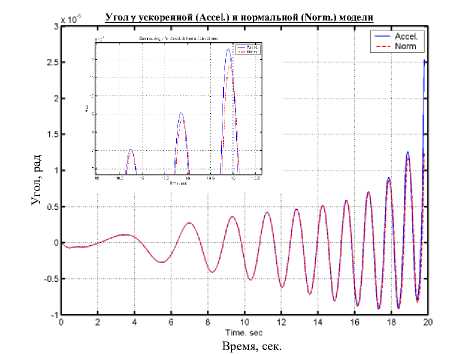
Рис. 8. Пример точности интегрирования ускоренной модели (без алгебраических цепей) и стандартного вида системы.

Рис. 7. Промоделированные стохастические воздействия: от неровностей пола и заедание в механизмах закрытого типа

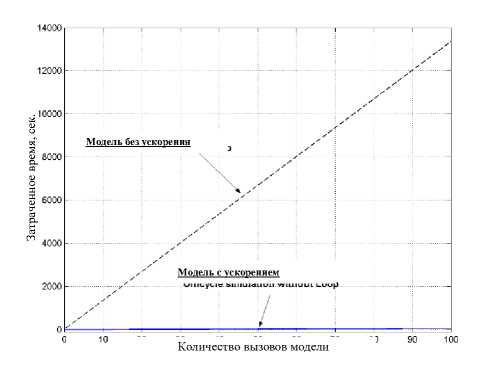
Рис. 9. Сравнение времени интегрирования моделей – без ускорения и с ускорением.

Схема 1. Диаграмма Simulink® компьютерного моделирования Одноколесного Робота-велосипеда: главная часть.

Производство энтропии угла наклона после обучения ННС уменьшилось в 10 раз. Для угла вращения и качания производство энтропии в 10 раз меньше в случае ПД-ГА и в 1000 раз меньше в случае нечеткого ПД контроллера, по отношению к классическому ПД контроллеру.

Однако, такой перенос энергии ведет к увеличению амплитуды угла наклона в случае ПД-ГА контроллера, что проводит к увеличению управляемого крутящего момента в системе управления педалями. Но после обучения ННС, движение в направлении наклона, становится гладким с маленькой амплитудой. Это подтверждает обучаемость и интеллектуализацию системы управления роботом.

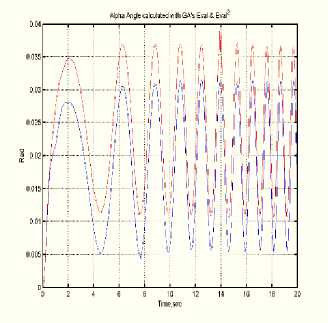
На рис. 11 показано сравнение результатов моделирования для двух функций принадлежности – Eval (5.3) и Eval². При этом все остальные параметры моделирования полностью совпадают – вид и параметры стохастического воздействия, количество генераций ГА и т.д. Как видно из рис. 11 а, движение модели происходит плавнее, что приводит к экономии ресурса системы в целом. Там же отображены изменения коэффициентов усиления kpl, kdl, кр2, kd2 уравнения управления (4.1) и (4.2).

.

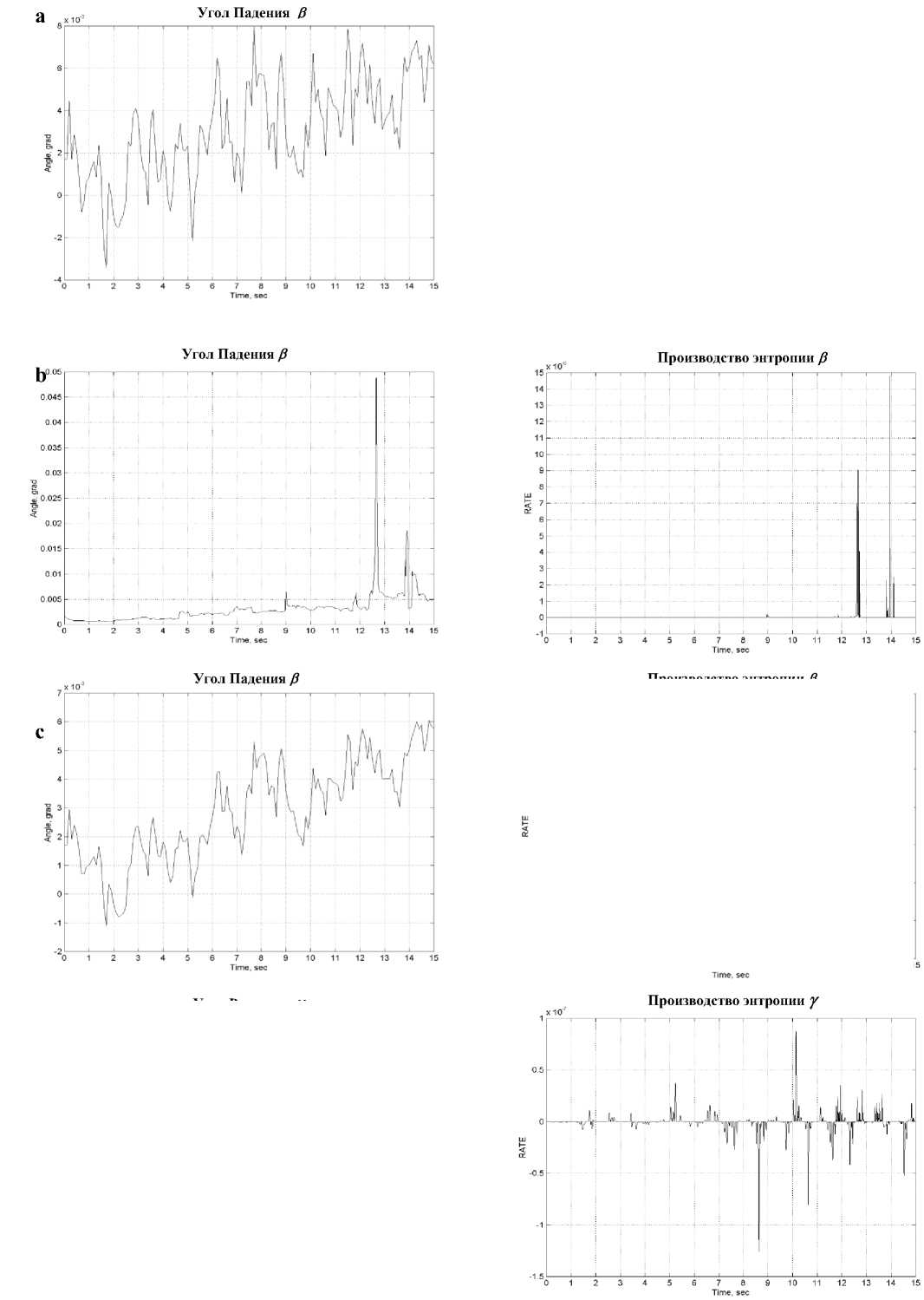
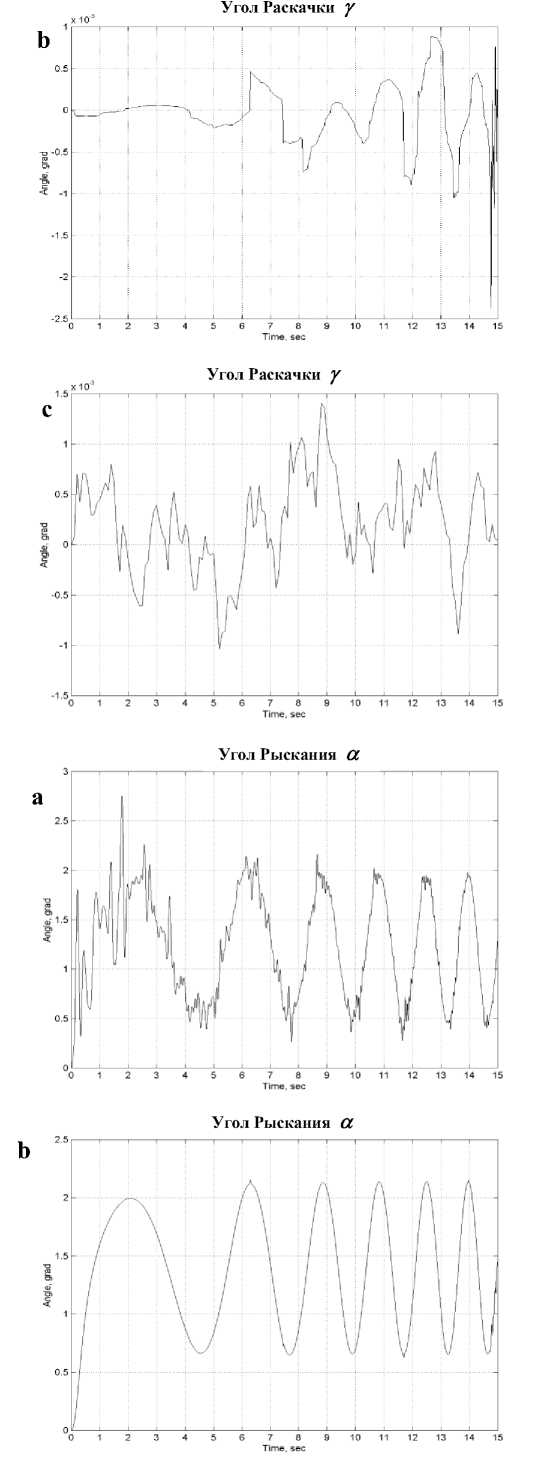
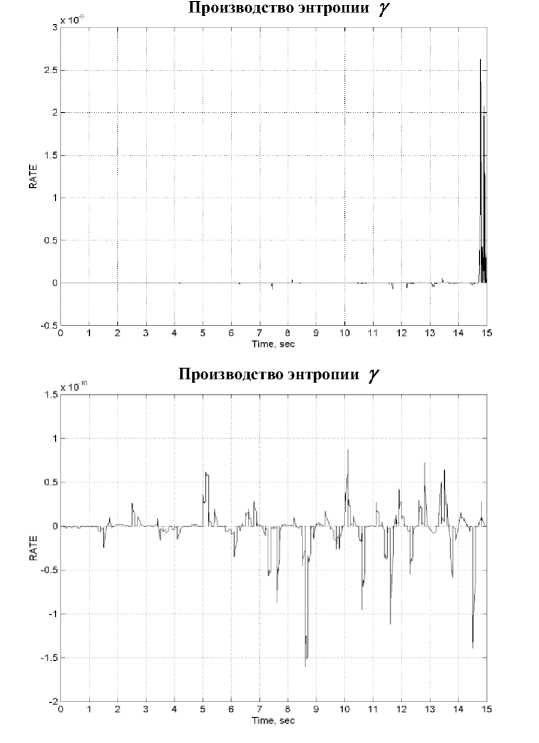
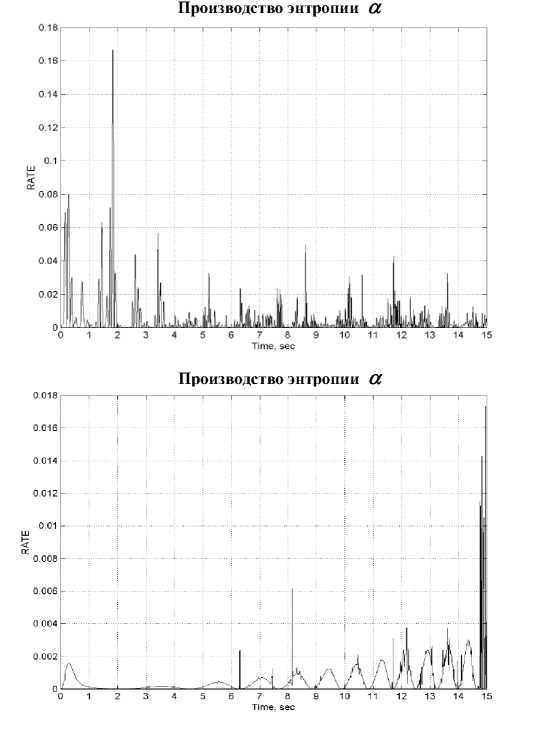
Рис. 10. Результаты стохастического моделирования модели одноколесного робота-велосипеда (прод.)

Приведенное усиление крутящего момента мех. закр. типа

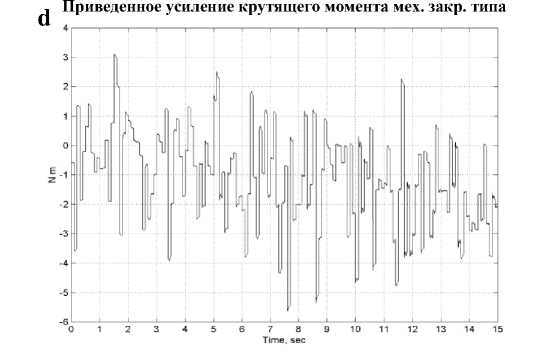
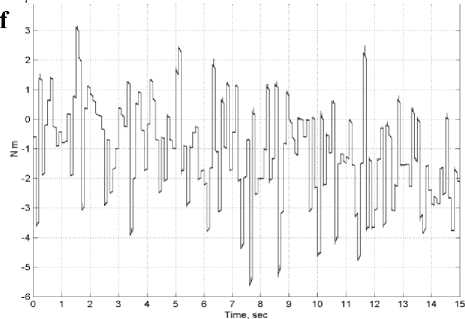
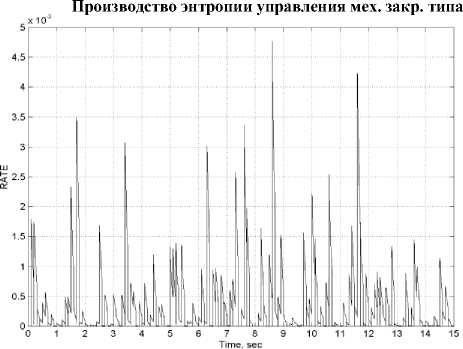
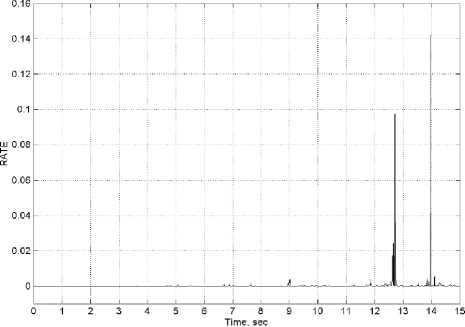
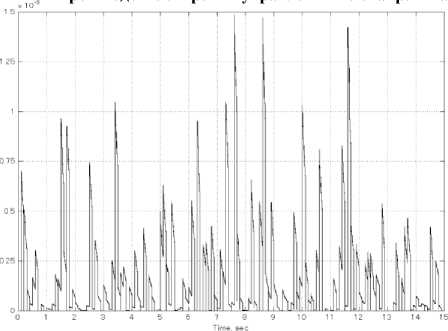
Рис. 10. Результаты стохастического моделирования модели одноколесного робота-велосипеда (прод.)

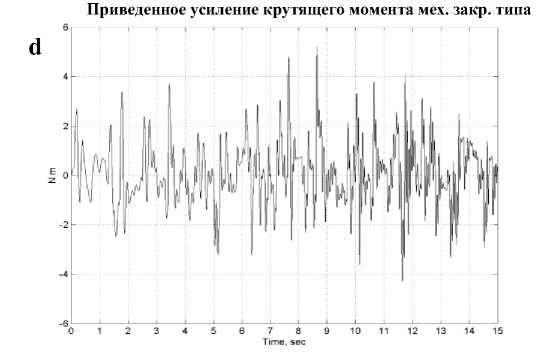
d

Приведенное усиление крутящего момента мех. закр. типа

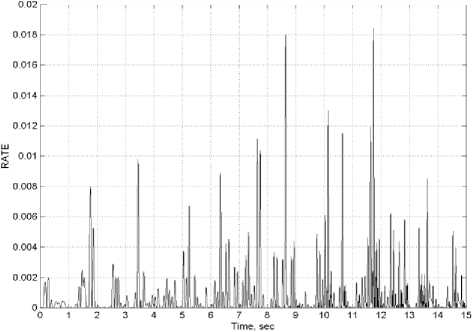
Производство энтропии управления мех. закр. типа

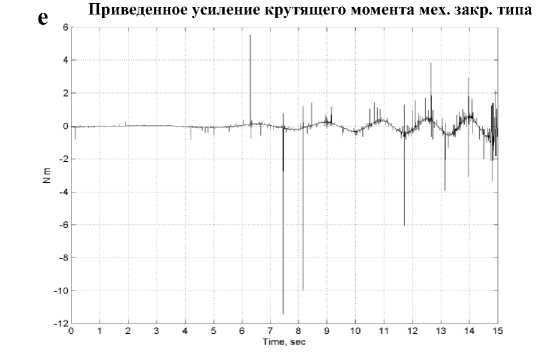
f

Приведенное усиление крутящего момента мех. закр. типа

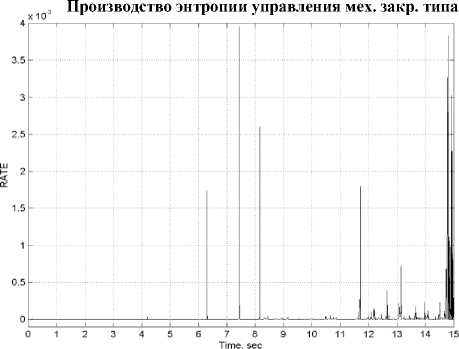
Производство энтропии управления мех. закр. типа

I1

Рис. 10. Результаты стохастического моделирования модели одноколесного робота-велосипеда: Механическое и термодинамическое состояние при управление: a) ПД регулятором; b) ПД-ГА регулятором; с) Нечетким ПДрегулятором;

Показатели усиления крутящих моментов и энтропии систем управления на: d) ПДрегуляторе; е) ПД-ГА регуляторе; f) Нечетком ПДрегуляторе

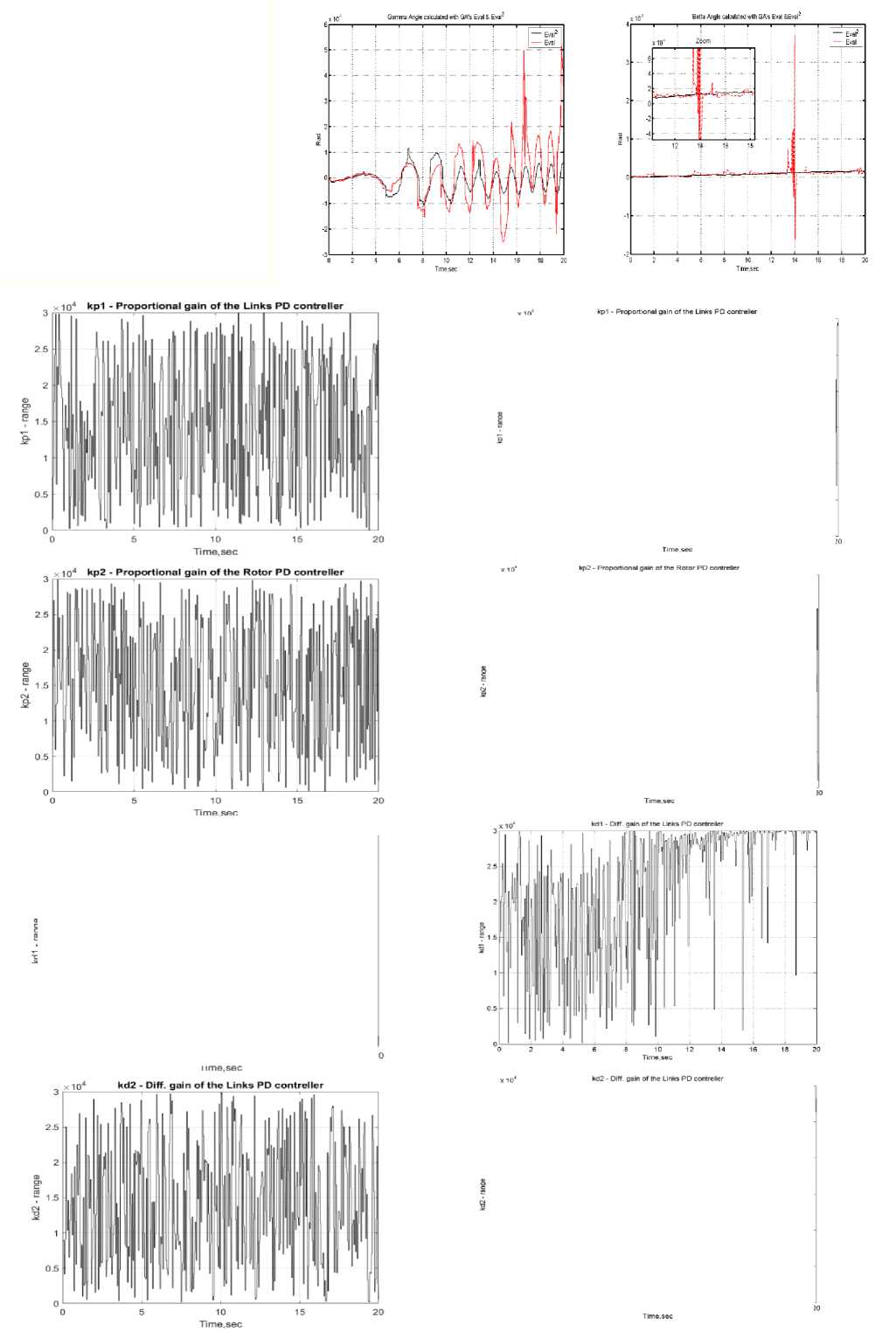
Рис. 11. Результаты стохастического моделир ₈ о ₂ вания ГА с различными функциями пригодности - Eval и Eval²

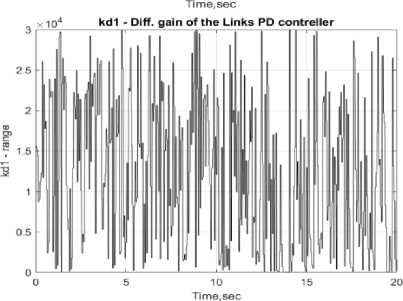
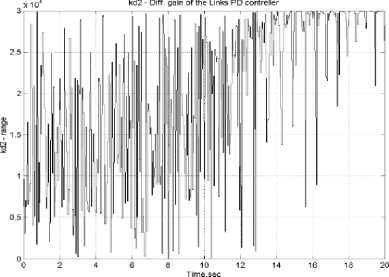
Введение функции пригодности ГА в виде квадрата обобщенной функции исключает управления, приводящие к локальной неустойчивости (отрицательному значению обобщенной энтропии). Как следствие, это дает улучшенные характеристики качества управления (минимальная сложность в реализации законов изменения коэффициентов усиления во времени, минимальные усилия приводящих механизмов и потери полезного ресурса). В этом случае полностью выполняется информационно-термодинамический закон компромиссного распределения противоречивых качеств управления (устойчивость, управляемость и робастность).

Обсуждение результатов эксперимента. Созданный в 1997-2000 годах робот показан на рис. 6. Полученные экспериментальные результаты представлены на рис. 12-13. Время натурного эксперимента ограничивалось 8 секундами ввиду неблагоприятного влияния дрифта сигнала гироскопических датчиков.

Отметим, что увеличение периода обновления управляющего сигнала более чем 0.001 секунды, в случае ПД контроллера, приводит систему к «падению» после 8-10 секунды.

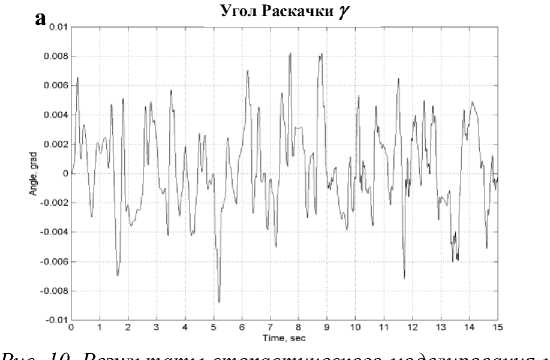
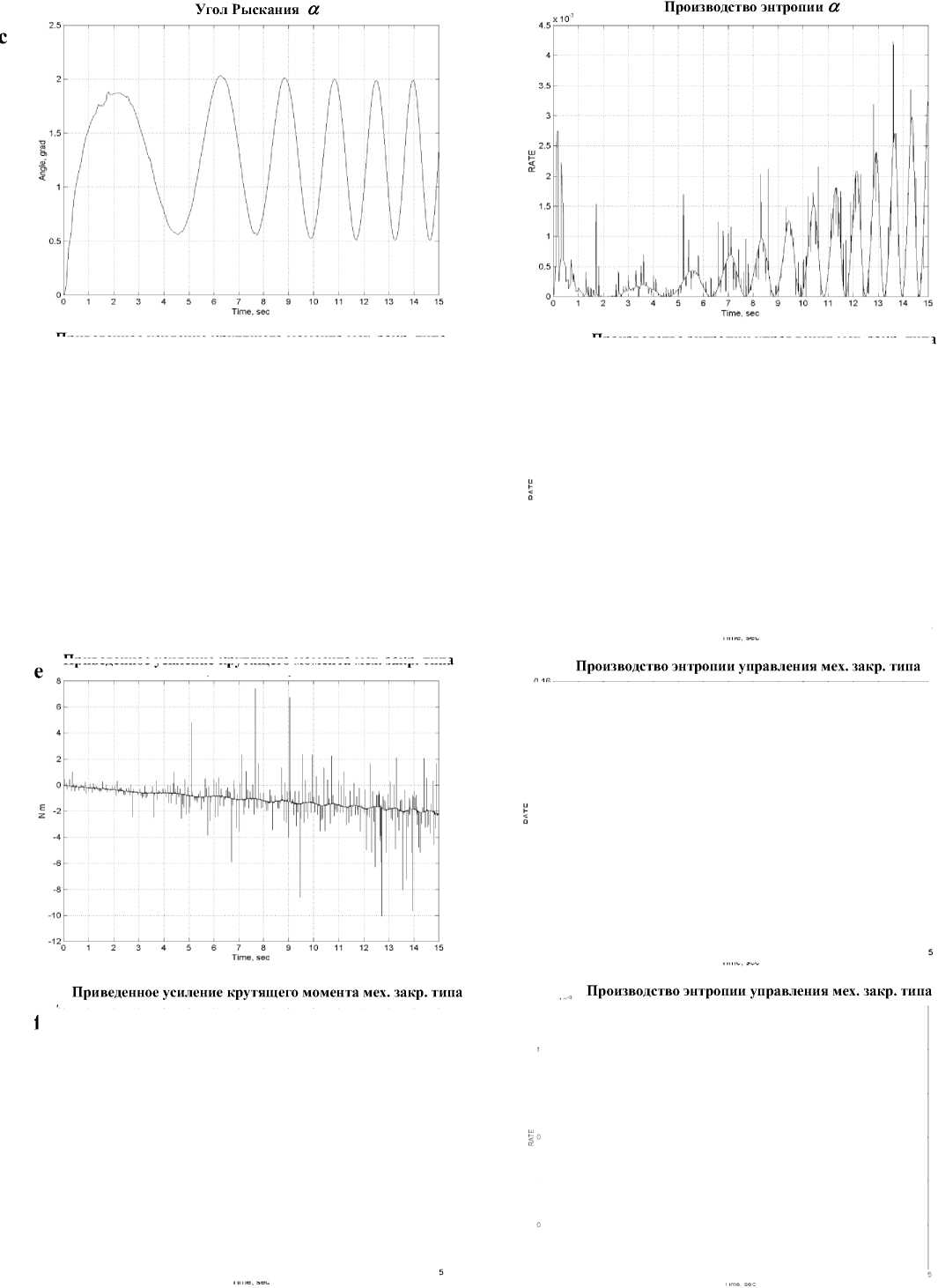
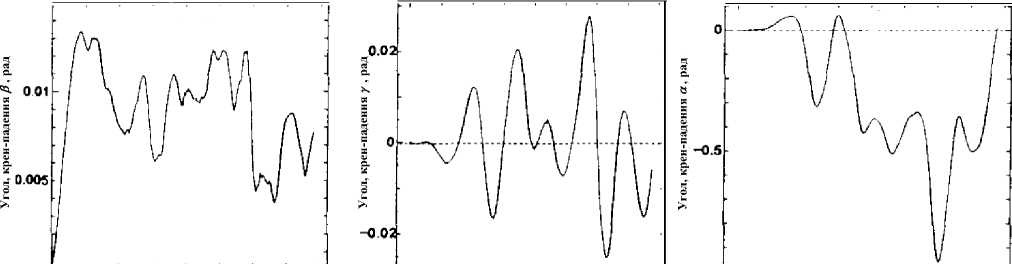
На рис. 12 представлены экспериментальные результаты модели бескабельного одноколесного робота-велосипеда. Как видно из результатов, устойчивость в направлениях: тангажа – раскачки γ , крена – падения β была успешно достигнута.

о ²        *        ^{8        8}           О 2        4        6 в ' О 2        4        6 в

Время, сек.                                              Время, сек.                                             Время, сек.

Рис. 12. Результаты эксперимента, углы - крен-падения β , тангажа - раскачки γ и рыскания α.

Время, сек.

Время, сек.

Время, сек.

Время, сек.

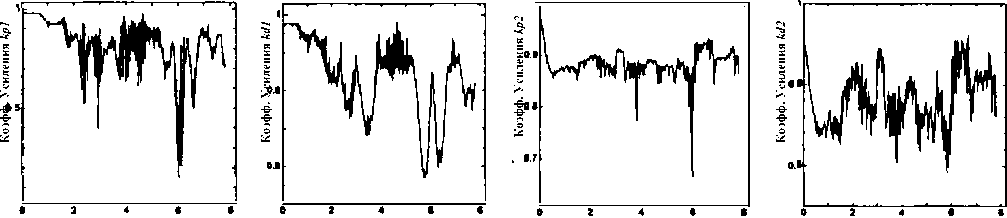
Рис. 13. Результаты эксперимента - поведение коэффициентов усиления kp1, kd2, kp2, kd2 двух нечетких PD контроллеров

На рис. 13 представлены результаты поведение коэффициентов усиления kp1, kd2, kp2, kd2 двух нечетких PD контроллеров (ур. 4.1, 4.2).

Из результата на рис. 11с видно - положение робота в направлении рыскания α быстро изменяется в процессе эксперимента, что указывает на удовлетворительное перераспределение энергии управления, обеспечивающую боковую устойчивость робота (тангаж Y и отслеживающую стохастические воздействия на модель (неровности пола, неоднородность трения в узлах и т.д.) за счет управлением углом рыскания α и углом крен-падения β.

Примечание. Полученные экспериментальные результаты были достигнуты с применением эмпирически сформированных функций фазификации и дефазификации для коэффициентов kp1, kd2, kp2, kd2 двух нечетких PD контроллеров, которые в свою очередь были сгенерированы на основании предварительных результатов моделирования GA с функцией пригодности – только снижение скорости производства энтропии системы управления, т.е. неполного процесса моделирования технологии мягких вычислений. Представленные выше результаты моделирования были получены позднее, по завершению - разработки мат-модели одноколесного робота-велосипеда (рис. 2, ур. 1.2), формирования технологии процесса мягких вычислений (рис. 3), а самое главное, возникновении возможности вычисления данного подхода – появления соответствующих вычислительных мощностей, без которых данный процесс был крайне затруднителен.

Примечание. Несмотря на это полученный результат, на тот момент и с теми вычислительными возможностями, приводит к подтверждению вполне удовлетворительной работы представленной структуры интеллектуальной системы управления. Представленная структура процесса, а также возникшие новые наработки в этом направлении, планируется полностью быть применены в новом прототипе – Автономном Пластичном (гибкий, вариативный) Одноколесный Роботе-Велосипеде.

Выводы

• -    В работе представлена основная идея интеллектуального управления динамическими, глобально неустойчивыми, нелинейными объектами на примере одноколесного робота-велосипеда. Основой этого подхода является качественный физический анализ динамического движения робота с введением интеллектуальной обратной связи в системе управления и реализацией в ней механизмов инстинкта и интуиции, основанных на ННС и ГА.

• -    Также представлены основные компоненты интеллектуальной системы управления, основанные на мягких вычислениях и определении робастности. Таким образом, происходит адаптация параметров двух нечетких ПД регуляторов и достигается устойчивое движение робота на конечном интервале времени (без изменения структуры исполнительного уровня системы управления).

• -    Введение двух новых механизмов в интеллектуальной системе управления основано на принципе минимума производства энтропии в движении робота и в системе управления. Нечеткое моделирование, термодинамических уравнений движения и интеллектуальной системы управления, подтверждает эффективность термодинамического подхода в решение проблемы анализа нелинейности системы и стабильности позиционного управления моделью робота.

• -    Таким образом, одноколесный робот-велосипед является новой Эталонной нелинейной управляемой динамической системой, с двумя (локально и глобально) неустойчивыми состояниями, и нечеткой интеллектуальной системой управления.

• -    Использование нечетких коэффициентов усиления в П(И)Д регуляторе, вычисляемых по таблицам решающих правил, адаптированных генетическим алгоритмом и сгенерированных нечеткой нейронной сетью, определяет способность использовать механизмы инстинкта и интуиции, в реальном масштабе времени, для интеллектуализации системы управления.

Сетевое научное издание «Системный анализ в науке и образовании»