Интеллектуальная система статистически значимой экспертизы знаний на базе модели самоорганизации неравновесной диссипативной системы

С развитием современных информационных технологий и широким внедрением в практику интеллектуальных систем (вычислительных систем, использующих алгоритмы искусственного интеллекта [1]), актуальным становится вопрос применения таких технологий в образовании [2–3]. Одной из таких проблем образовательного процесса, где без применения алгоритмов искусственного интеллекта просто не обойтись, является задача объективной экспертизы знаний учащихся с последующей классификацией их по группам успеваемости.

Действительно, при решении данной задачи возникает два существенных аспекта. Во-первых, если в качестве эксперта, оценивающего знания учащегося, выступает преподаватель, то результат его работы, по определению, является субъективным. Конечно, можно снизить уровень этого субъективизма, сформировав экспертную группу, но это явно экономически невыгодно, особенно при проведении промежуточной аттестации. Во-вторых, результатом экспертизы знаний являются шкальные данные (2, 3, 4, 5). И здесь существенен вопрос построения этой шкалы. То есть, способ преобразования номинальных («категориальных») данных представлений эксперта о знаниях учащегося (например, «знает»–«не знает»), в ограниченную упорядоченную шкалу натурального ряда. Оба отмеченных аспекта относят вопрос экспертизы знаний в область плохо обусловленных задач, корректное решение которых возможно только с использованием интеллектуальных систем.

При решении данной проблемы на сегодняшний день можно выделить два пути. Во-первых, самый многообещающий – это создание экспертных обучающих систем (ЭОС) [1–4]. Однако, значительная сложность проектирования программных комплексов, использующих технологии и алгоритмы экспертных систем [1], делают перспективу широкого применения ЭОС в образовании весьма отдаленной. Во-вторых, получивший наибольшее распространение в настоящее время путь – это применение для экспертизы знаний разнообразных тестовых заданий, использующих бинарные данные (возможны только два варианта: задание либо «зачтено» – 1, либо «не зачтено» – 0). При выполнении учащимся теста формируются вторичные данные, представляющие собой, как правило, доли или проценты и позволяющие проводить дальнейшую математическую обработку результатов. Сегодня существуют и успешно применяются, как внутривузовские программные комплексы для тестирования, построенные, например, на базе LMS Moodle, так и крупные, содержащие большие банки заданий по различным предметам, системы, такие как «Единый портал тестирования НИИ МКО».

Однако, подход, построенный на использовании тестов для экспертизы знаний, тем не менее не лишен отмеченного выше недостатка, связанного с неоднозначностью формирования шкалы оценок [5–8]. Фактически, в данном случае, речь уже идет о разделении студентов на группы (по схожести оценки), на основании результатов тестирования, выраженных в процентах, и вычислении пороговых значений для каждой группы. Как правило, эти пороговые значения определяются на основе номинальных («категориальных») данных, формируемых экспертом, что, естественно, никак не снижает уровень субъективности проводимой экспертизы. Предложенная в работе интеллектуальная система реализована в виде программного комплекса на языке Python. Статистическая обработка проводилась с использованием системы статистической обработки данных R.

Цель работы состоит: во-первых, в выработке подхода к экспертизе знаний учащихся, полностью лишенного элементов субъективности, построенного на принципах самоорганизации неравновесных диссипативных систем и математической статистике, что позволит сделать её результаты статистически значимыми; во-вторых, в разработке вычислительной системы, позволяющей реализовать предложенный подход.

Статистический анализ исходных данных

Для решения поставленной задачи необходимо, в первую очередь, провести статистический анализ данных о характере выполнения студентами тестовых заданий. Для этого была сформирована статистическая выборка участников эксперимента. В нее вошли 94 студента I курса, изучающие одну и туже дисциплину по одинаковым учебным планам. Каждый студент получал одинаковое количество тестовых заданий. Тем самым обеспечивалась репрезентативность выборки участников. В качестве заданий использовались тесты «Интернет-тренажера» на «Едином портале тестирования НИИ МКО». На основании результатов тестирования означенных студентов была сформирована выборка данных. Особенности работы «Интернет-тренажера» позволили обеспечить выполнение принципов составления выборок: повторность и рэндомизация. Большой банк вопросов, доступных на режиме «Интернет-тренажер» на «Едином портале тестирования НИИ МКО» обеспечил репрезентативность выборки данных.

В качестве основных величин для составления выборки данных использовались следующие параметры: суммарное количество вопросов, на которые конкретный студент дал ответы; суммарное количество правильных ответов этого студента (рисунок 1). Кроме этих двух параметров для оценки скорости выполнения тестовых заданий в выборку включалась такая величина, как эффективное среднее время ответа на один тестовый вопрос (таблица 1), определяемая соотношением:

t =

1 L-nl~ 1 a,

где n – количество выполненных тестовых заданий; t i – время, отведенное на выполнение i -того тестового задания; a i – число ответов, данных при выполнении i -того тестового задания. Данный параметр позволяет контролировать такой аспект тестирования, как самостоятельность выполнения студентом заданий.

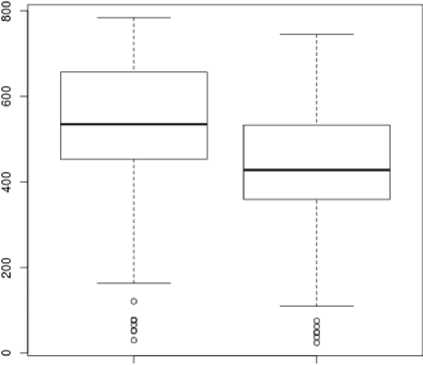
questions                      answers

Рисунок 1. Боксплоты выборки суммарного количества вопросов, на которые даны ответы (quеstiоns), и выборки суммарного количества правильных ответов (answers)

Figure 1. Boksploty total number of questions that were answered (questions), and a sample of the total number of correct responses (answers)

Действительно, как следует из данных, приведенных в таблице 1, время выполнения одного тестового задания лежит в пределе от 23 секунд до одной минуты.

Таблица 1.

Квартили выборки эффективного среднего времени ответа на один вопрос (мин)

Table 1.

Quartiles effective average response time for one question (min)

0%	25%	50%	75%	100%
0,137	0,373	0,563	0,999	5,744

Если же этот параметр выходит за эти границы, то возможно предположить, что студент не сам выполнял порученное ему задание, что должно сказаться на результатах экспертизы его знаний.

Что касается других величин, боксплоты которых представлены на рисунке 1, то анализ этих данных показывает, что при таком плотном характере распределений, при которых медианы для questions и answers различаются на 20%, а межквартильные интервалы – всего на 13%, определение пороговых значений, формирующих различные шкальные группы, является непростой задачей. Действительно, об этом свидетельствуют и данные, представленные на рисунке 2.

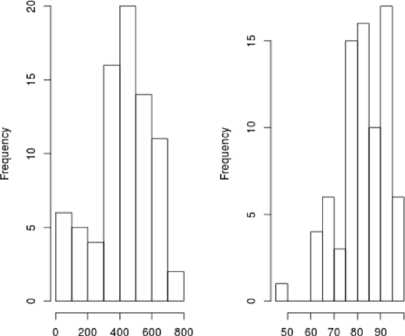
Рисунок 2. Гистограммы распределений количества правильно данных ответов (а) и процентов правильных ответов (б)

• Figure 2.    Histograms of distributions coli-operation right data responses (a) and procent correct answers (b)

Очевидно, что гистограммы, отображенные и на рисунке 2, а , и на рисунке 2, б не отражают нормальное распределение или хотя бы близкое к нему. Доказательством этого утверждения является и графический тест на проверку нормальности распределения, представленный на рисунке 3. Поскольку точки не ложатся на прямую, проведенную через квартили, распределение нельзя считать нормальным. Кроме того, анализ данных, представленных на рисунке 2, показывает, что представленные на нем гистограммы имеют многомодовую структуру. То есть, они отражают характеристики нескольких групп. Вычисление же пороговых значений для различных групп (построения шкалы оценок), регулярными методами является неразрешимой задачей, что приводит нас к отмеченной уже выше необходимости использования интеллектуальных систем.

Проведенный первоначальный статистический анализ данных о результатах тестирования студентов, позволяет на основе полученных выводов сформулировать способ построения шкалы экспертных оценок, отвечающих условию статистической значимости разделения на оценочные группы. То есть, объективность выставляемой экспертной оценки в данном случае базируется на математических принципах.

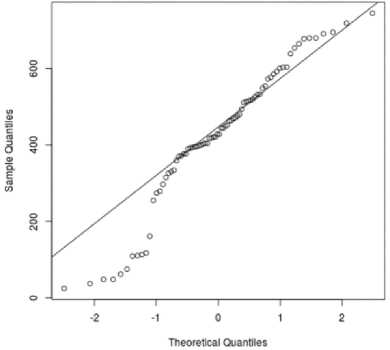
Рисунок 3. Графический тест нормальности распределения для данных answers

• Figure 3.    Graphical test normality distribution of data for answers

Способ построения экспертных оценок

Как уже отмечалось выше, при построении шкалы экспертных оценок на основе результатов тестирований необходимо определить пороговые значения для различных оценочных групп. Как правило, для этого используются вторичные данные, проценты выполнения тестовых заданий. Однако, эти данные не несут всей полноты информации о характере выполняемой студентом работы, тем более если экспертиза знаний построена не на одном единственном тесте (в этом случае она бы была лишена репрезентативности). Кроме того, при анализе совокупности выполненных тестовых заданий, использование процентов сильно искажает реальную картину. Например, представленные на рисунке 2 гистограммы, свидетельствуют, что суммарное количество правильных ответов (рисунок 2, а ) и процент правильных ответов (рисунок 2, б ), характеризуются разными распределениями.

В данной работе шкала экспертных оценок строилась на основании анализа совокупности значений множества X = { x _{t j} }.

x i ,1

Здесь x, , = i , j

x i ,2

– вектор, характеризую-

кx,3 J щий результаты тестирований -того студента.

Компоненты вектора: x,1 = qt - суммарное количество вопросов на которые -тый студент дал ответы; x,2 = a, - суммарное количество правильных ответов этого студента; x,3 = t , -среднее эффективное время ответа на один вопрос -тым студентом.

В вузах используется четырехбалльная система оценок. Таким образом, задача экспертизы знаний студентов сводится к разделению множества X на 4 непересекающихся подмножества. Для этого удобно использовать алгоритм кластерного анализа k- mean [7]. Он разделяет множество элементов векторного пространства на заранее известное число кластеров. Преимущества этого алгоритма для решения поставленной задачи состоит в следующем: во-первых, количество кластеров в нем задается изначально (4 в нашем случае), во-вторых, он не требует значительных вычислительных затрат и прост в реализации.

Минимизацией суммарного квадратичного отклонения точек кластеров от их центров:

D = ZE( xj - ^>) ^ min (2) i=4 j ^ Ki можно добиться качественного разделения множества исходных данных на непересекающи-еся подмножества. В этой формуле: μj – центры масс векторов; Kj – множество векторов -того кластера xj e K,,.

В данном случае снимается и основная проблема этого алгоритма, некачественное разбиение на кластеры из-за попадания в ловушки локальных минимумов зависимости (2) при определении начальных значений центров кластеров. Это достигается следующим способом. Допустимые интервалы значений координат векторного пространства делятся на 4 равных отрезка. Центры кластеров для начального приближения определяются координатами средины этих отрезков.

Результаты кластеризации представлены на рисунках 4 –5. Для построения шкалы оценок вычисляются абсолютные значения множества векторов X :

R = JZ x,²               (3)

V , = 1

Маркированные элементы этого подмножества для которого значения R наибольшие, соотносятся с максимальной оценкой. Таким образом, полученные в результате кластеризации подмножества, сортируются в порядке убывания абсолютных значений и соотносятся с соответствующей шкальной величиной (5, 4, 3, 2).

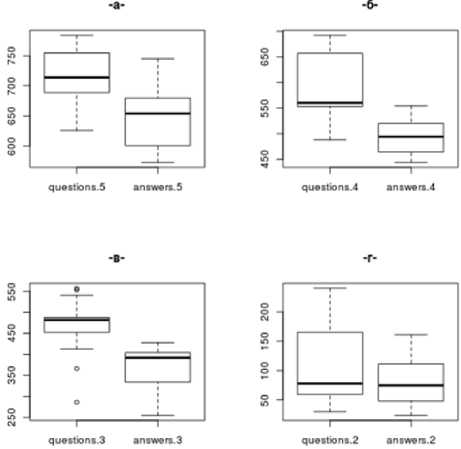
Рисунок 4. Боксплоты распределений, полученных в результате кластеризации исходных данных, представленных на рисунке 1, в зависимости от качества ответов: 5 (а), 4 (б), з (в) и 2 (г)

Figure 4. Boksploty distributions obtained from clustering raw data shown in Figure 1, depending on the quality of the responses: 5 (a), 4 (b), 3 (c) and 2 (d)

Given : rating

0        500       «00       «0       800

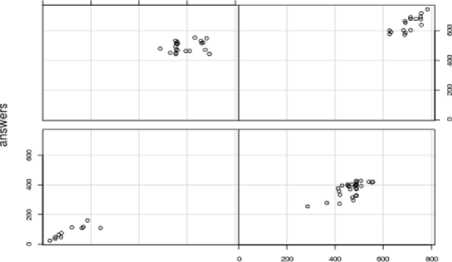
Questions

Рисунок 5. Точки подмножеств кластеров в соответствии с соотнесенными с ними рейтинговыми оценками

Figure 5. The points of subsets of clusters according to their correlation with the rating assessment

Различные студенческие группы неоднородны, и по гендерному составу, и по психологическим и когнитивным характеристикам, а также по интеллектуальному уровню. Иными словами, группа студентов представляет собой неравновесную диссипативную систему. Формировать в такой системе жесткие критерии шкалирования при проведении экспертизы знаний (пороговые значения для классификации студентов), практически невозможно. В любом случае, при формулировании таких критериев присутствует значительная доля субъективности эксперта. При этом границы принятия решений оказываются непредсказуемо размытыми, а на ширину этих границ оказывает влияние огромное количество факторов.

Алгоритм кластеризации, используемы в предлагаемом способе, снимает все эти ограничения. Как уже отмечалось выше, такие алгоритмы опираются на саму структуру данных, определяя в ней определенные особенности. Происходит, так называемый, процесс добычи данных (data mining). Каждая группа студентов формирует свою уникальную структуру данных, которая отражает, выше означенные особенности, характерные для данной выборки.

При этом для каждой группы формируются свои пороговые значения для получения шкальных оценок экспертизы. Кроме того, предлагаемый в работе подход, позволяет реализовать такую модель экспертизы, при которой она бы строилась на явлении самоорганизации в неравновесной диссипативной системы, каковой и является группа обучающихся. Для этого необходимо постоянно увеличивать, в определенный период, количество тестовых заданий, выдаваемых студентам. При этом в группе формируются устойчивые паттерны учащихся, преуспевающих в освоении дисциплины. Между ними начинается соревнование за лидерство. Такой паттерн выступает в качестве локомотива, организующего активность остального контингента группы. При этом в каждой группе происходит самоорганизация в соответствии с индивидуальными интеллектуально-психологическими особенностями обучающихся. Иными словами, реализуется принцип конкуренции и соревновательности, что позволяет добиваться высоких результатов в группе в целом.

Заключение

Получена интеллектуальная система, преобразующая набор интервальных данных в шкальные, основываясь на самой структуре исходных данных. Это главная особенность предлагаемого способа экспертизы знаний, что дает неоспоримые преимущества перед другими подходами.