Intelligent Control for a Swarm of Two Wheel Mobile Robot with Presence of External Disturbance

Published Online November 2019 in MECS DOI: 10.5815/ijmecs.2019.11.02

Formation control is one of important issue in research community which attracted large amount of attention .They are needed for systems that capable of performing complex tasks which can’t be solved by a single agent. The multi agent system (MAS) was the solution to these complex tasks where the number of agent cooperative with each other to reach the best solutions. The approaches of MAS can be found in different sides such as : Synthetic aperture radar (SAR) ,multi unmanned aerial vehicles (UAV) , for military reconnaissance missions , civilian applications , rescue missions , agent which work as parameter for specific equation and others .The main requirement for managing multiple robots , aircrafts or space crafts is bullied a cooperative system to accomplish the objective.[1]

Managing the multi - robot system basically consists of two parts : the operation to be controlled such as path tracking , object picking , wall painting ,...etc. and the control method used to enable performing of these tasks in appropriate manner. Path tracking for examples can be determined in different ways .There are a three categories for solving the mobile robotic path : The first one, use of dynamics environments with mobile obstacles .In this case the robot uses its on-board sensors to be compatible with any changes in the environments .Path planning is the second category ,in this case there is a prior map for the workplace ,path execution is to be performed using optimization algorithm based on minimum distance and time. The third one is designing a driving control for robot to follow the desired path with minimum tracking error. These controllers are used to eliminate the effect of disturbance and time delay on the velocity and angle of orientation.[2]

The parameters of these controllers can be optimized using intelligent system to minimize the error .There are many optimization algorithms which search for the best solution.Particle swarm optimization is one of heuristic optimization method based on bird flocking with nature-inspired, decentralized and self _organized characteristics .It consist of number of particles which move toward the best personal local position, basically these particles randomly interactive with each other to move toward the best global position with appropriate velocity .The velocity V and position P of particles are updated by the following equation :

Vi (t + 1) = WVi(t) + Ciri(PbeSt(i,t) - Pi(t))

^{+ C}2 r 2⁽ g best^- P i^{(t)) (1)}

Pi(t+1) = Pi(t) + Vi(t+1) (2)

where :v represent the velocity ,ω is the inertia weight that balance the global exploration and local exploitation r 1 , r₂ are random number between[0,1], c 1 , c₂ are positive constant number denote the acceleration coefficient . The first part of (1) called “inertia “ and it present the previous velocity while the second part called “ cognitive “ it encourage the particle to move toward the best own position .Third part known as “cooperation “,it shows the collaborative effect of the particle to find the global optimal solution. Fig. 1 presents a flowchart of general PSO.[3]

Many advances of PSO are introduced such as modification of PSO which contain a little change in origin one, hybridization of PSO which combine the PSO with the other article intelligent algorithm like GA ,Fuzzy an others.

PSO with linearly decreased inertia weight ( PSO_LDID) was one of these algorithm that update the inertia weight as follow :

to = to_max(to_max - to_min) * (iter/maxite ) (3)

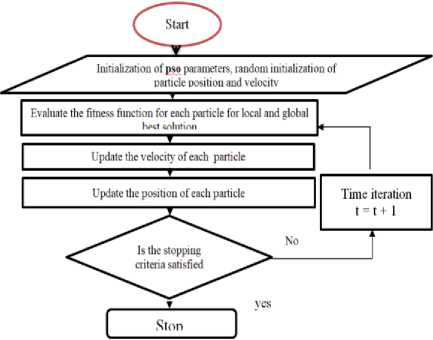
Fig.1. Flowchart of general PSO.[4]

where ω max , ω min denote the maximum and minimum value of the inertia weight respectively , iter denotes the current iteration , maxiter presents the maximum number of iteration .Large value of inertia weight good for global exploration and smaller value contribute to the local optimization.[5,6]

Another type of PSO algorithm was proposed with a time - varying acceleration coefficients (PSO-TVAS) . C 1 , the cognitive acceleration coefficient is linearly decreased .C 2, ,the social acceleration coefficient is linearly increased which is shown as follows :

C1 = (c1f — c1i) * ((maxiter - iter) * maxiter) + c1i (4)

C2 = (c2f — c2i) * ((maxiter - iter) * maxiter) + c2i

Where c 1i , c₂ i are the initial value for cognitive and social coefficient respectively and c 1f , c₂ f are the final value for them .[7]

A novel RODDPSO is proposed for reducing the possibility of getting trapped in the local optima and expand the search space .In this algorithm a randomly occurring time delays that reflect the history of previous best local and global position is introduced in velocity updating model as declare below :

Vi (k + 1) = toVi (k) + Ci ri (pi (k)- xi (k))

+ C2 r2 (Pg (k) - xi (k))

+ т^сзГзЕ? a(T)(Pi(k - t) - xi(k)) +mg©C4r4ZN a(T)(Pg(k - t) - x^))     (6)

Where : ω is the inertia weight declare in (3) . c 1 ,c 2 are the acceleration factor calculated by (4)and(5).c 3 ,c 4 are the acceleration coefficient of distributed time delay time delay , N is the upper bound of time delay dimension. α(τ) represent the vector of time delay that occur randomly . m i (ƹ) , m g (ƹ) are the intensity factor of the distributed time delay for evolutionary state (ξ).The evolutionary state can be one of the following convergence state denoted by ξ=1 , when the particles try to fly into the global optimal region as soon as possible .

Exploitation state denoted by ξ =2 , when the particles exploit the region around personal best particles.

Exploration state denoted by ξ =3 , the particles explore the entire search space thoroughly.

Jumping out state denoted by ξ =4 ,In this state the particles are try to escape out of search space .[8]

Table 1. Show the updating strategy for distributed time delay .

Table 1. Time delay updating strategy

State	Mode	ml(ξ)	mg(ξ)
Convergence	ξ(k) = 1	0	0
Exploitation	ξ(k) = 2	0.01	0
Exploration	ξ(k) = 3	0	0.01
Jumping-out	ξ(k) = 4	0.01	0.01

II. Propblem Difination

One of major problem in multi robot system is how to maintain the path for swarm of robots in turbulent enviornments.The effect of disturbance can be elimnated by using a specific controller .Intelligent controller one of method that can be used for this purpose.In this article tuning PID controller with new modified optimization algorithm is introduced as a one solution for this propblem.

А =

« 1	0	0		" 6 1
0	0	1	• В =	0
0	0	«2.		. 62

-2c

(Mr2 +2IW)

—

” • «=[.

62-l

= -2.6876

]

III. Multi Agent System

The multi-agent systems may be a parameter for specific processing, different parts of machine/robot or a group of robots. In a multi robot systems, many robots moving together according to specific topology and path. Moving in formation produces many benefits such as increase the efficiency and robustness of system , reducing the required cost in systems specially in configuration and adding new elements. The multi agent system in this article consist of swarm of two wheel mobile robot .In this articles the three robots is built by MATLAB 2018a Simulink as shown in Fig. 2 and Fig. 3 which presents the Simulink model for single and three robots respectively while the physical parameters of this robot is selected from (Altamiro,2004) and represented as follow[9,10] :

« 1

-2cZ2		= -5.1193	(9)
« 2	(Ivr2+2IWZ2)
61	_    kr	= 0.824147	(10)
	_ (Mr2 +2IW)
6 2	-krl	= 2.2087	(11)
	~ (Ivr2+2Iwl2)

The robot path is determine using A* algorithm with cell decomposition method . The map of work space is converted to binary form , each obstacles represents by one and free space represent by zero .The path is computed for single robot and other robots path determine according to the leader follower equations as follow:

Table 2. Physical parameters

Parameters	Value
Moment of inertia around C.G. (I v)	0.4732 Kg.M2
Distance between right and left wheel (I)	0.36m.
Viscous friction factor (c)	0.15833 Kg/s.
Mass (M)	24Kg.
Moment of inertia of wheel (I w )	0.0198 Kg.M2
Radius of wheel®	0.057m
Driving gain factor (K)	1.7.

X2 = X1- b2icos (T21), У2 = У1 — b2i sin(T2i) (12)

X3 = X1 - b3i€Os(T3i), Уз= У1 -b3i sin (T31) (13)

Where 2,3 (follower) and (leader) represented by 1, b21 , b31 are the distance between leader and follower2 and followerl respectively , T21 , T31 are the angle between line projecting from the coordinates of follower2 and follower2 to the leader .PID controllers shown in Fig. 2 are tuned using PSO,HPSOGA,RODDPSO and new proposed method in order to eliminate the effect of external disturbance that may occur in system. The integral absolute error (IAE) of system is computed for each algorithm .The error in this experiments is the summation of angle and velocity error.

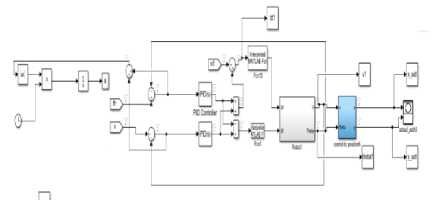
Fig.2. The Simulink Model of Single Robot

The dynamic model of robot represents according to the following equation :

х = Ах + Ви , Y=C x          (7)

Where :

IV. Proposed Method

The new proposed method combine the randomly occurring distributed time delay particle swarm optimization with genetic algorithm , the historical best local and global position are used to update the velocity model .The evolutionary states are classified in to four region ( convergence , exploitation , exploration , jumping – out ) for using them to specify the delayed intensity factor that used in velocity update. The speed and velocity updating model use a new population of particles which generated by the genetic algorithm rather than a current one, So new population is updated using early delayed information of personal and global optimum. The main goal of this proposed method is to prevent divergences of particles form the local optimum in addition to avoid the premature convergence . The parameters used in the Simulink present in table 3.

• V.    Simulation process

Table 3. Parameters of Simulink.[9]

Number of swarm	3
Number of particles in each swarm	20
Acceleration factors c1,c2	1 ,1.3
Inertia wait w	Updating according to(3).(Dynamic)
Sample time	0.005
Solver	20
Upper timer	0.15
Mutation rate	0.01

The steps of new proposed algorithm can surmised by the following steps

• 1-    Initialize all the parameters of RODDPSO as shown in table 3.

• 2-    Generate the first population randomly, evaluate the fitness of all particles and define the global and local best positions.

• 3-    Calculate the mean distance (d i ) between particle i and other particles , this operation repeated for all particles and it is represented by the following :

di = £^1 ^^-х^2   (14)

Where S is the size of swarm and D is the dimension of particle

• 4-    Use the following equation to compute the evolutionary factor E f of each particle

Edg-dmin f dmax-dmin

Where d g is the global best mean distance particle , d min and d max is the minimum and maximum mean distance of d i.

5- Classify the evolutionary state ^k according to

equal division strategy as		follow
fl,	0.00	< E/	<	0.25
к	0.25	< Ef	<	0.50
^k — k      3,	0.50		<	0.75
[4,	0.75		<	l.00

• 6-    Update the inertia weight according to (3).

• 7-    Use table1 to update the randomly distributed delay information.

• 8-    Generate new population of particles using genetic algorithms.

• 9-    Update velocity and speed for each particles.

The simulink model for this expermints is prsented in Fig.3. .From Fig.3. , the general controller generate the desired path for three robots using A* algorithm.The PID parametrs selected by optimixation algorithms.The robot block present the dynamic model of two wheel mobile robot .Disturbane generator add disturbane to system either constant or dynamic.Disturbance(n1) presnt the place where the disturbance is added.

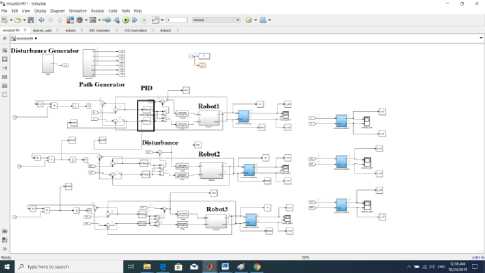
Fig. 3. Simulink Model of System

• VI.    Simulation Results

  This experiment tests the ability of maintaining the desired path for swarm of three robots with presence of external disturbance .This disturbance is supposed to occur from PID controller to the right wheel of mobile robot .Three cases of disturbance are tested ,these are: constant disturbance with value of 100 and 1000 , dynamic disturbance and pure environments. The test is applied with a varying number of iteration for each algorithm. PID controller is tuned with four algorithms (PSO , RODDPSO, HPSOGA , Proposed algorithm ) in order to determine which of them can enhance the performance of path tracking.

Table 4 shows the total IAE for three robots with presence of constant external disturbance of value (100) .Each algorithm is tested with varying number of iterations. It is clear that the minimum IAE is produced by the proposed algorithm with value 1.19248E-05 at iterations 40, the second best result produced by HPSOGA with IAE value 1.92E-05 as demonstrated in Fig. 4 .

Table 5 shows the IAE for three robots with presence of constant 1000 as constant external disturbance. From table ,the minimum IAE is produced by proposed algorithm with value 3.143E-05 in 40 as shown in Fig.5.

Table 6: shows the IAE for three robots with presence of dynamic disturbance in 40 iterations. Also the minimum IAE is produced by proposed algorithm with value 1.174E-05 .

The new proposed algorithm proved their efficiency in pure environments by producing minimum IAE with value 2.64E-05.

The results show that’s proposed algorithm produced minimum IAE for system than other three methods with slightly decreasing of error throw higher iterations while the other method alternate in their performance throw iterations.

Table 4. Error for three robots with 100 constant disturbance

Table 6. IAE for three robots with Dynamic Disturbance for 40 iterations

Error	PSO	RODDPSO	HPSOGA	Proposed
Robot1	2.907E-05	2.93E-05	1.235E-05	6.403E-06
Robot2	6.905E-07	1.20E-05	1.07E-05	1.276E-06
Robot3	2.221E-05	8.51E-06	1.59E-05	4.06E-06
Total	5.197E-05	4.978E-05	3.893E-05	1.174E-05

N.	PSO	RODDPSO	HPSOGA	Proposed
10	4.84E-05	4.20374E-05	4.69E-05	4.03639E-05
20	4.99E-05	7.925E-05	6.45E-05	2.20777E-05
30	3.64E-05	2.94769E-05	1.92E-05	3.40148E-05
40	3.33E-05	2.98984E-05	2.31E-05	1.19248E-05

Table 5. IAE for three robots with 1000 constant disturbance

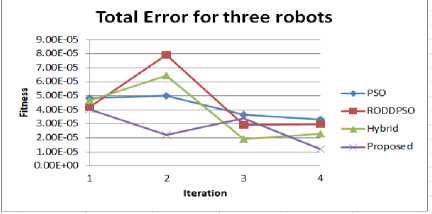
Fig.4. The fitness function for three robots with 100 constant Disturbance

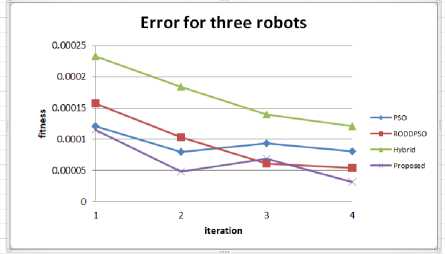
Fig.5. IAE for three robots with 1000 constant disturbance

VII. Conclusions

This articles produces a new proposed optimization algorithms for tuning the PID controller of swarm of two wheel mobile robot. The PID controller is used in each robot to control the velocity and angular torque of each wheel .The external disturbance is added to the signal form PID controller to the right wheel .The results proven that system produces minimum IAE when the PID controller is tuned by the new proposed method. The proposed method uses the historical information of local and global optimum to update the velocity and speed of new population. It add the distributed time delay to velocity equation of PSO with a particles generated by GA .The algorithm was tested in three cases which are constant external disturbance, dynamic external disturbance and free environments , the results show that proposed algorithm is the best for keeping the desired path of three robots as possible by producing the minimum IAE. In future work the new algorithm can be used for tuning the non-linear PID controller , also it can be combine with fuzzy and other intelligent system.

N.	PSO	RODDPSO	HPSOGA	Proposed
10	0.0001213	0.000157	0.0002328	0.0001156
20	7.988E-05	0.0001031	0.0001843	4.833E-05
30	9.391E-05	6.139E-05	0.0001401	6.95E-05
40	8.083E-05	5.464E-05	0.0001212	3.143E-05

Table 7. IAE for three robots in free disturbance environments

algorithm	Itr.	Robot1	Robot2	Robot3	Total error
PSO	10	3.46E-05	3.46E-05	1.77E-05	8.70E-05
	40	4.69E-05	1.05E-05	9.25E-06	6.66E-05
ROD-DPSO	10	1.03E-05	2.52E-06	4.85E-05	6.13E-05
	40	3.73E-05	1.17E-06	1.95E-05	5.80E-05
HPSOGA	10	7.33E-06	5.07E-06	2.82E-05	4.06E-05
	20	8.10E-06	7.76E-06	1.93E-05	3.52E-05
Proposed	10	9.30E-06	1.02E-05	7.56E-06	2.71E-05
	40	6.33E-06	1.60E-06	1.85E-05	2.64E-05