Intelligent Controller for Synchronization New Three Dimensional Chaotic System

• I.    Introduction

  In parallel with industrial and technological improvement, control systems and their control methods have become sophisticated. Control of new systems using previous old methods has become difficult. Further, considering human brain patterns and abilities in order to control and solve problems has resulted in emergence of new intelligent controlling methods which utilizes human brain operation patterns which are mentioned below. Brain Emotional Learning Based Intelligent Controller (BELBIC) was introduced for the first time by Lucas in 2004 [1]. Brain Emotional Learning Based Intelligent Controller (BELBIC) is an example of bioinspired control

methods which is based on limbic system of mammalian brain. This controller is based on emotional behaviors in biological systems. Emotion is an emergent behavior in biological systems for fast decision making in complex environments. The advantages of this behavior cannot be neglected in creature survival [2]. During the past few years, the BELBIC has been used in control devices for several industrial applications. The BELBIC has been successfully employed for making decisions and controlling linear and nonlinear systems such as, Brain Emotional Learning Intelligent Controller (BELBIC) for the control of two benchmark nonlinear plants was applied in [3]. In [4], a problem of speed tracking of permanent magnet stepper motor has been discussed based on the static PID and newly type of intelligent control which mimics the emotional learning in limbic system of mammalians. Also BELBIC was used to control the Locally Linear Neuro-Fuzzy Model (LOLIMOT) of Washing Machine [5]. BELBIC was applied to a Switched Reluctance Motor (SRM) to tackle the speed and position control problem in [6]. Furthermore, BELBIC was applied for real time positioning of laboratorial overhead traveling crane in [7]. In [8], BELBIC was applied to electrically heated microheat exchanger, which was a nonlinear plant. In [9], BELBIC is introduced to stabilize uncertain nonlinear systems via robust adaptive method. Also an intelligent adaptive approach for aerospace launch vehicle control is presented in [10]. Furthermore, the design of PID and BELBIC controllers in path tracking and controlling problem is studied in [11] and finally an intelligent autopilot control design for a 2-Dimensional helicopter model is studied in [12].

In this study, utilizing BELBIC model introduced in [11, 12], we will design an intelligent controller to synchronized two new 3D chaotic systems [13]. Simulation results depict that this proposed controller can synchronize these chaotic systems better than Active Control [19, 20]. Finally, the parameters of BELBIC are improved by swarm intelligent algorithms.

The rest of the paper is organized as follows. The Brain Emotional Learning Based Intelligent Controller (BELBIC) is described in section 2. The new 3D chaotic system is described in section 3. Synchronization between two new 3D chaotic systems by BELBIC is proposed in section 4. Parameters of BELBIC are improved by Evolutionary Algorithms in section 5. The conclusion of this study is provided in section 6.

• II.    Brain Learning Based Intelligent Controller (BELBIC)

In this method, emotional factors like excitement and anxiety are the roots of learning. Here, the roots of anxiety are assumed as some stimulants and the control system should react in the way that reduces the anxiety of the system caused by these stimulants. The Brain Emotional Learning (BEL) is divided into two parts, very roughly corresponding to the amygdala and the orbitofrontal cortex, respectively. The amygdaloid part receives inputs from the thalamus and from cortical areas, while the orbital part receives inputs from the cortical areas and the amygdala only. The system also receives reinforcing (REW) signal. The emotional learning model in amygdala and orbitofrontal corex is illustrated in Fig 1.

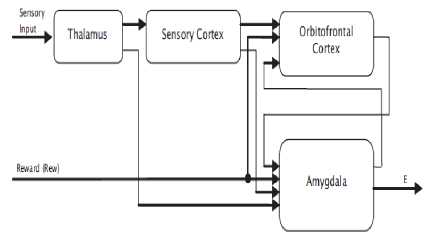
Fig. 1. Scheme of BELBIC structure [1]

BELBIC has some input sensors that can be chosen by designer. Each input sensor has two different states that can be described as.

=

=                         (1)

In which s, is the input sensor and v,w are two states that are depended on input sensor. Index i represents the iTh sensor and its related states. These two equations will be updated by following equations [11, 12].

∆  =       (0,    -∑  )

∆  =   (   -∑  -∑  -    ( ))    (2)

In which α,β are training coefficients and rew is the reward signal. Amygdala acts as an actuator and orbitofrontal corex acts as a preventer. Therefore the control signal of BELBIC is:

=∑  -∑

This paper uses the continuous form of BELBIC. In continuous form the BELBIC states are updated by following equations.

̇=   (   -)

̇ =    (    +   +   -  )

A BELBIC controller has to be designed to synchronize two chaotic systems. For traction force sensory inputs are considered.

= e is the error between the master system and the slave system. The structure of the control system is illustrated in Fig 2.

Fig. 2. Control system configuration using BELBIC

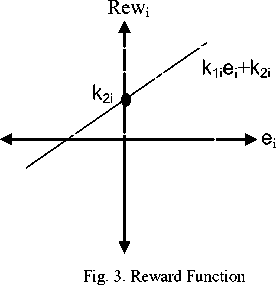
The reward signal will be obtained the reward function. This function has a great role in BELBIC. The designer must define a reward function that has its maximum values in the most desired regions. In this study, the reward function is chosen as a linear function of system error.

= + (6)

and are the positive parameters of the reward function. The reward function for this BELBIC controller is as Fig 3.

• III.    System Description

Recently, Dadras and Momeni proposed the threedimensional autonomous chaotic system that generating two, three and four-scroll attractors [13]. The system is described by:

̇= у - ax + byz

̇= cy - xz + z              (7)

̇= dxy -ℎ z

Here x,y,z are the state variables and a,b,c,d,h are the positive constant parameters. When a=3,b=2.7,c= 4.7,d=2,h=9 , the system (7) is chaotic witn the Lyapunov exponents Lj_ =0.631, L2 =0,L3 = -7.931 . The corresponding phase portraits are depicted in Fig 4 and the state trajectory of the system (7) is displayed in Fig 5.

10 -

5J

0 J

-5

-10

-15

5 x State y State 0

-5

-10

Fig. 4. Phase portraits of the 3D chaotic attractors (7) in (a) the xy space, (b) the xz space, (c) the yz space, (d) the xyz space.

• IV.    Synchronization Between Two New 3D Chaotic System

In this section, the BELBIC is applied to synchronize between two new 3D chaotic systems. Suppose the driving system takes the following froms:

̇=   - ах_г + by^z^

3̇i=    - X1Z! + Z1(8)

̇ =-ℎ ^1

Fig. 5. State trajectory of the 3D chaotic attractors (7).

And the response system is presented as follows

^̇2=   - ax₂ + by₂z₂ + U! ( t )

3̇2=     - X2Z2 + z2 + U2 (t)

2 ̇2=       -ℎ ^Z2 + ^3 ( t )

Where и_г ( t ), 1^2 ( t ) and IZg ( t ) are control functions to be determined to achieve the synchronization between two systems (8) and (9). Define state errors between system (8) and (9) as follows

^x =   -Xl ey =   - У1

^Z =   -

We obtain the following error dynamical system by subtracting the driving system (8) from the response system (9).

t ̇ x =   ^- o,e_x + b ( V2^Z2 ^- yiZi)+Ui ( t )

̇У=    + e_z -( x₂z₂ ^- x₁z₁)+ U₂ ( t )     (11)

̇ ⁼( x₂y₂ ^- Х1У1)-ℎe_z + u₃ ( t )

Thus, the error system (11) to be controlled with control inputs u (t), u2 (t) and u3 (t) as functions of error states e,ey and e . When system (11) is stabilized by control inputs u2_ (t), u2 (t) and u3(t) , e,eу and e will converage to zeroes as time t tends to infinity. Which implies that system (8) and (9) are synchronized.

To achieve this purpose, Input sensory of BELBIC is chosen as (12).

№ =

{ s₂ =                        (12)

Ьз =

The reward function’s parameters for the BELBIC controller are as follows.

( rew! = к ₁e_x + к 2 rew₂ = к₃е_у + к^            (13)

г ew3 = к 5ez + к 6

The parameters a and /? are equal to 1 and 3 respectively. We take the reward gains as к ; = 1 for i = 1,2,3,4,5,6. For drive and response systems, we take initial conditions (x₁ (0),y₁(0),z₁(0)) = (-5,26,14) and (x 2 ⁽0),y 2 ⁽0),Z 2 ⁽0)) = ⁽24,2,-6) . After using BELBIC, we compare the results with the results obtained by Active Control [19]. Synchronization errors ( e_x , e_y, e_z) of BELBIC and Active Control [19] in new 3D chaotic systems are shown in fig 6 and fig 7. The time response of the control inputs (u ₁,u₂, u₃) of BELBIC and Active Control [19] to the synchronize new 3D chaotic systems are shown in fig 8 and fig 9. The time response of (x,y, z) states for drive system (8) and response system (9) via BELBIC is shown in fig 10.

-25

0    0.01   0.02   0.03   0.04   0.05   0.06   0.07   0.08   0.09   0.1

Time (sec)

Fig. 8. The time response of the control inputs (иг,и2,и 3) via BELBIC.

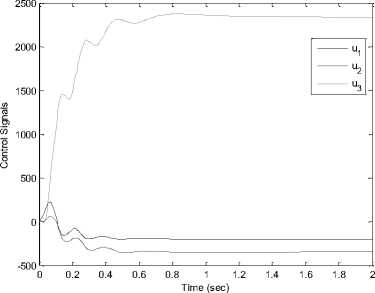
Fig. 9. The time response of the control inputs (иг,и2,и 3) via Active

Control [19].

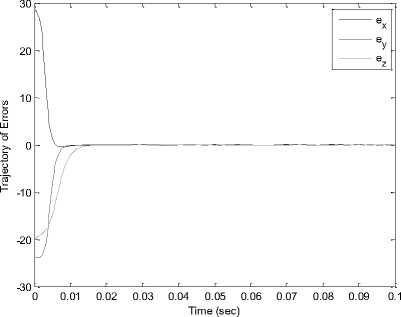
Fig. 6. Synchronization errors (ex, ey, ez) in drive system (8) and response system (9) via BELBIC.

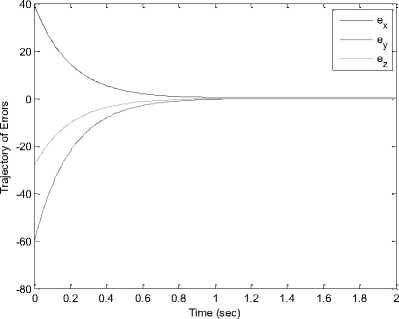
Fig. 7. Synchronization errors (ex, ey, ez) in drive system (8) and response system (9) via Active Control [19].

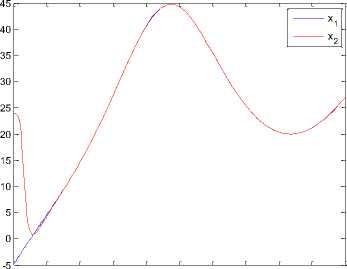
0    0.01   0.02   0.03   0.04   0.05   0.06   0.07   0.08   0.09   0.1

Time (sec)

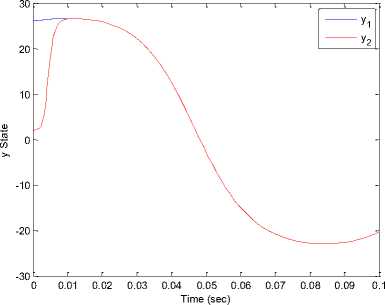
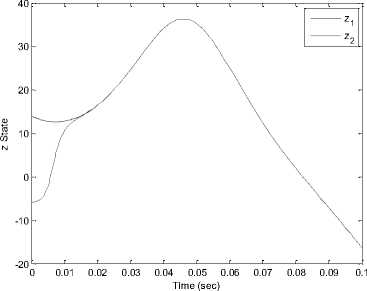
Fig. 10. The time response of signals (x, y, z) for drive system (8) and response system (9) via BELBIC.

• V.    Improving the Parameters of Controller

The reward signal is very important for BELBIC. The system responses differently to each value. It is necessary to select proper parameters to obtain a good response because the improper selection of parameters leads to inappropriate responses or even may lead to instability of the system. The Genetic Algorithm [14,15], Cuckoo Optimization Algorithm [16], Particle Swarm Optimization Algorithm [17] and Imperialist Competitive Algorithm [18] are used to search the optimal parameter (k) in order to guarantee the stability of the systems by ensuring negativity of the Lyapunov function and having a suitable time response. The reward signals in the equation (13) are optimized by the Cost Function in the equation 14. The selected cost function is defined to minimize the least square errors. The cost function enforces the synchronization errors to decay to zero rapidly.

f (ei,e2 ,-,e„)=^7Z^F        (14)

Table 1. Genetic Algorithm Parameters.

Parameters	Values
Size population	80
Maximum of generation	30
Prob.crossover	0.75
Prob.mutation	0.001
к Search interval	[1 10]

Table 2. Cuckoo Optimization Algorithm Parameters.

Parameters	Values
Size clusters	2
Maximum number of cuckoo	80
Size initial population	5
Maximum iterations of cuckoo	30
к Search interval	[1 10]

Table 3. Particle Swarm Optimization Algorithm Parameters.

Parameters	Values
Size population	80
Maximum iterations	30
Initial and Final value of the global best acceleration factor	2 and 2
Initial and Final value of the inertia factor	1 and 0.99
к Search interval	[1 10]

Table 4. Imperialist Competitive Algorithm Parameters.

Parameters	Values
Number of Initial Countries	80
Number of Decades	30
Number of Initial Imperialists	8
Revolution Rate	0.3
к Search interval	[1 10]

The optimal parameters of reward signals using genetic algorithm, cuckoo optimization algorithm, particle swarm optimization algorithm and imperialist competitive algorithm are listed in table. 5.

Table 5. Optimal Parameters of Reward Signals.

	к	^2	^3	к	к	k	a	/?
GA	3.55	1.26	6.01	8.02	3.46	9.49	9.46	1.09
PSO	3.79	6.27	5.64	3.97	2.92	8.11	7.19	1.53
COA	10	7.54	10	8.58	1.66	10	8.51	1.28
ICA	4.03	1	5.89	10	1	10	10	1

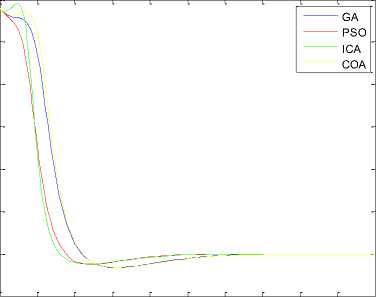
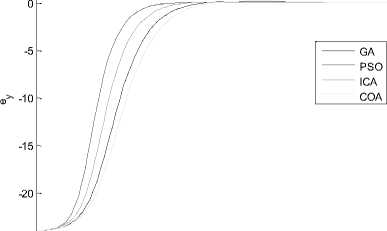
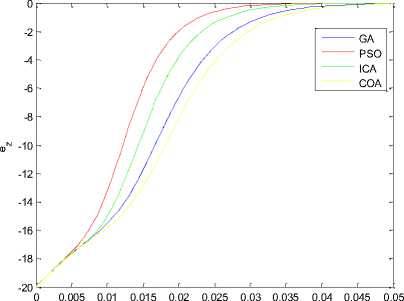
Synchronization errors (ex, ey, ez) in new 3D chaotic systems are shown in order Fig 11 to Fig 13.

-5

0   0.005  0.01  0.015  0.02  0.025  0.03  0.035  0.04  0.045  0.05

Time (sec)

Fig. 11. Synchronization error (ex) in drive system (8) and response system (9).

-25

0   0.005  0.01  0.015  0.02  0.025  0.03  0.035  0.04  0.045  0.05

Time (sec)

Fig. 12. Synchronization error (ey) in drive system (8) and response system (9).

Time (sec)

Fig. 13. Synchronization error (ez) in drive system (8) and response system (9).

• VI.    Conclusion

In this work, Chaos synchronization have been discussed. Many methods synchronized chaotic systems but many above-mentioned methods can only applied some given chaotic systems, some methods will produce the singularity problem in synchronizing the chaotic system and most of the methods in the literatures need more than one variable information of the master system. In order to achieve a proper synchronization between two new 3D chaotic systems, an intelligent controller based on brain emotional learning (BELBIC) was utilized. The BELBIC consists of reward signal which accepts positive values. Improper selection of the parameters causes an improper behavior which may cause serious problems such as instability of the system. Evolutionary Algorithms were well known optimization methods. Genetic Algorithm, Cuckoo Optimization Algorithm, Particle Swarm Optimization Algorithm and Imperialist Competitive Algorithm optimized the BELBIC. For this reason these algorithms minimized the cost function to find minimum current value for it. On the other hand cost function found minimum value to minimize the least square errors. Finally, it has been proved that the controller is faster, more optimal and more efficient than active control.