Intelligent Geometric Classification of Irregular Patterns via Probabilistic Neural Network

Published Online March 2015 in MECS

Multi-class pattern classification emphasizes issues including neural network architecture, deciphering schemes, and training methodology [1] using either a combination of some small neural networks or a large one [2]. First essential step of obstacle avoidance control in AUVs is to detect them based on vision. In this method the received image from camera is remotely transferred to the controller, and then images are processed to recognize the obstacles. The obstacle detection is the most critical stage of robotic control accomplished via collecting and analyzing the received data. A classification method employing two consecutive stepped neural networks is used to categorize the received images based on the boundary interpretation of different patterns. Accuracy of class numbers is verified by the available database; ultimately, applying this process makes underwater vehicles capable of underwater obstacles’ interpretation and avoiding them.

Amongst the ANNs being trained to carry out feature extraction [3-6] , SOMs [4, 7] ,and Hopfield ANNs [8] have apparently drawn researchers’ attention. Feedforward ANNs have also played a significant role in lots of the reviewed pattern classification issues [9-12] . Neural networks applications are widespread for their acceptable performance in classification and function estimation. They have been utilized with success in medical image analysis [13] for diagnosis of diseases [14] hearts sound classification [15] , automatic face recognition [16] and other various applications.

A suitable deduction of feature extraction is the chief key in image processing’s efficiency. An innovative neuro-fuzzy network is suggested which employs a simple Fourier transform method to extract features[17]. The proper Learning rules guarantees the results’ accuracy, for instance, Hebbian learning rule is used in a chaotic neural network [18] and given an acceptable performance. Many researches have been done to modify the neural network function by presenting new accurate algorithms. The SVM is relatively a new pattern classification approach based on the ideas of large margin and mapping data into a higher dimensional space, as pointed out in[19, 20]. Elsewhere, a neural network model is proposed based on the concept of multi-layer perceptron trained under limitation of layers weights to a certain range to meet the least squared error [21]. Image Interpolation algorithms are simulated and learned by adjusting weights and bias values of neural networks based on camera identification methods [22]. pattern classification approach[23, 24] with different types of neural network has already been derived; some higher-order neural networks for distortion invariant pattern recognition[25], identifying salient features for classification in both feedforward neural networks[26] and probabilistic neural networks[27], classification of relevant features in the input vector by applying radial basis neural network[28], and employing multilayer perceptron neural network for the classification of remote-sensing images[29, 30] are several citable studies in this case.

The operational regions of ROVs including oil pipelines, underwater tankers and reservoirs of oil and fresh water on sea bottom and welded bonding of marine structures can be detected and surveyed by the robots programmed with image classification system, so the operation is completely held intelligent without any user interference. Images could be captured online by a camera mounted on underwater robot, then, two successive neural network acts as pattern reorganization which correspond each image to the most suitable class amongst 50 various geometric patterns and sub-classes as well. Initially, the first neural network relates a shape sample to the most pertinent pattern; continuously, the second neural network is applied to recognize the relevant sub-class. The presented algorithm strengthens the ability of underwater robots to analyze the sea floor soil and discover the best location for pipe laying, data acquisition systems, and underwater transducers.

• II.    Performance algorithm

Interpretation of shapes and classification of them consists of two stepped neural network, the first step of which relates each input sample to the best suited of fifty initial category of images and the second one of which assigns that to the pertinent subclass. The images have been read as TIF formatted and then are changed to binary form to be compatible to digital computers. In the previous comparable work [31] the author applied two-staged artificial neural network based on the hole image ¹ interpretation to classify five elementary geometric shapes of circle, semi-circle, rectangular, square and triangle. To achieve this purpose they considered and used constant moments [32] as feature extractions; these moments are obtained from second and third order moments of a geometric shape. This trend costs elaborate and time consuming mathematical calculations. Derivation of Eigen-vectors for irregular and complicated images such as the ones applied in this paper is not logical and applicable.

Here, a much simpler and more efficient method is suggested for pattern reorganization considering irregular and chaotic images. The extracted feature is defined as histogram of boundary point’s distances relative to an optional defined point on the image’s boundary. The distances are divided by maximum length between boundary points to make dimensionless output, so rotation, translation, distortion, and scale variance have no effects on the histogram. Consequently, this method is used as viable criteria to determine the categories of image samples. Figure1 shows some image samples and their relevant subsamples used as the input of neural network classifier. Rotation, translation and distortion are derived on the images as is clearly seen; these variations may weaken the performance of neural network, but on the other hand generalize the case and cover more portion of reality.

The paper deals with a specific form of neural networks, Probabilistic neural network, as a type of Radial basis function network. In each set of classes, fifteen samples are allocated in train and five in test. The architecture of PNN network is designed as is demonstrated in figure2. Figure 2 illustrates the applied neural networks consist of four layers: input layer, pattern layer, summation layer and output layer. The input layer’s neurons are equal to feature vector dimension formed by x-y coordinate points of normalized distance histogram (NDH). The first hidden layer’s, pattern layer, neurons are equal to the number of training samples, 750, and the second hidden layer, summation layer, has 50 neurons as numbers of classes. The summation units simply sum the output of the pattern units, and then corresponds it to the category where the pattern belongs. The output layer is in binary type, so relevant class takes unit value and other classes take zero.

Probabilistic neural networks uses a supervised training set to develop probability density functions within a pattern layer. Key advantage of PNN is the fast training process in spite of large memory requirements. PNN model is the best credit scoring in classification in comparison to other statistical methods considering more accurate output [33] . The dataset used for performing benchmark on PNN must be split into at least two parts: one part on which the training is performed named training set, and another part on which the performance of the network is tested named testing set. The input sample with unknown category is propagated in the pattern layer. In the pattern layer the difference between input vector and trained vector is calculated and then every component is multiplied by respected bias through operation of transfer function. Here the nonparametric techniques are developed for estimation of multivariate p.d.f. from random samples using the multivariate Gaussian approximation in the first hidden layer as is indicated below:

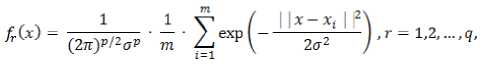
Where i is the (vector) pattern number, m is the total number of training patterns, x i is the i-th training pattern from category (class) Ω r , p is the input space dimension, and σ is an adjustable "smoothing" parameter using the training procedure. The network is trained by setting the W i , weight vector in one of the pattern units equal to each x pattern in the training set and then connecting the pattern unit's output to the appropriate summation unit.

Hyperbolic tangent sigmoid transfer function is employed in the second hidden Layer.

fr(x) = a = tansig(x) = 2/(1 + exp(—2 *x)) - 1

The objective is reducing error, e, which is the difference between the neuron response, a, and the target vector, t. The learning rules calculate desired changes to the weights and biases and initialize them in each layer, so update the weights in the direction along which the overall square error is reduced the most [34] .

By multiplication of the second layer input to weights, the summation of the elements in each k classes are calculated by a transfer function that is used to estimate the probability vector for each class. The transfer function, C(x) set the maximum value of output components to unit that shows the respected class.

C(x) = argmax { p_i ( x ) cost_i ( x ) apro_i ( x )}, i = 1, 2,..., c

Where C(x) denotes the estimated class of the pattern x, and m is the total number of classes in the training samples. Where cost i ( x ) is the cost associated with misclassifying the input vector, and apro i ( x ) is the prior probability of occurrence of patterns in class c .

Generally, two feature extraction methodologies, normalized distance Histogram (NDH) and dimensionless geometrical modules (DGM), by which image interpretation has been possible, are applied to two-stages PNNs. Continuously, each output of which is obtained and evaluated to have a good insight into choosing the best strategy in classification of both heterogeneous patterns and homogeneous ones.

• III.    Classification

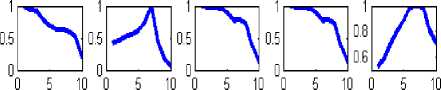
The coordinates of entire points located on the images’ boundaries are read via image processing techniques, and then the distances between the reference point and all the other points on the boundary is calculated and normalized by division to the maximum value of computed distance. In the figure3 the distance between reference point and boundary points, and the maximum distance are shown by d and D, respectively. Applying such image reading process, all the values of normalized distances lay between zero and one as is shown in figure 4. The NDH is introduced to neural network as characteristic of both patterns and its sub-samples though variety the NDH would remain so closed in the second step. For instance, if consider a classic automobile as the input image and its dimensions change into a larger or smaller scale or rotate, the designed neural network interoperates the shape as the class of automobiles. In figure5 the NDH for each image is plotted in a defined domain of 0 to 10 on x axis. To have a better outlook on the image interpretation, three classes regarding their subsamples are clarified in figure 6.

Performance of neural network in the first stage is illustrated in the following diagrams. The figure 7

demonstrates the results of classification of fifty different shape patterns. Percentage of the accurate training samples’ interpretation is 98.4 % which is acceptable in classification subjects. The vertical axis indicates the class number and the horizontal one represents the samples’ number. The blue circle shows the accurate class and the solid red circle is the class recognized by neural network; Coincidence of blue points and red circles proves that the neural network has performed precisely. As it is illustrated in figure 7 all samples of class six has distinguished correctly but about the class thirteen, one of them is categorized to the wrong class. Altogether, generally it is seen that the designed neural network is pretty powerful in interpretation of patterns. The percentage of correct recognition of training samples is calculated by the formula below:

^cZoss ^ ^-Training Sample ^wrong recognition

^-class ^ ^Training Sample

/50x15-12 A _{x 1Q0 = 9g 4%} V 50X15 /

The figure 8 demonstrates the performance of the testing network for five remaining samples of each pattern group; a section of this drawing is magnified in figure 9 to give a higher resolution of network performance. The percentage of correct distinction of test samples is obtained equal to 91.6%; this value verified the neural network’s acceptable function.

• IV.    Sub-classification

First neural network can efficiently interpret images and obtain their relevant class amongst the fifty basic categories extracting geometrical features. Also, each of these basic classes is divided into several close patterns with little difference defined as subsamples. Therefore, for more specific and detailed classification, the second neural network is employed in second stage of intelligent detection to match the images to the closest subclass. In order to design the second neural network, two different algorithms are utilized for feature-vector extraction; the first one refers to NDH, and the other one is construed as dimensionless geometrical modules (DGM) [31].

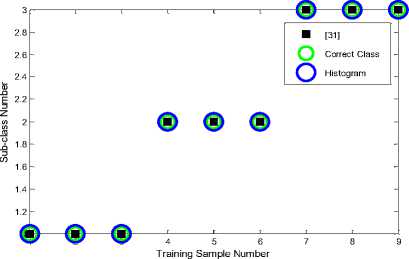
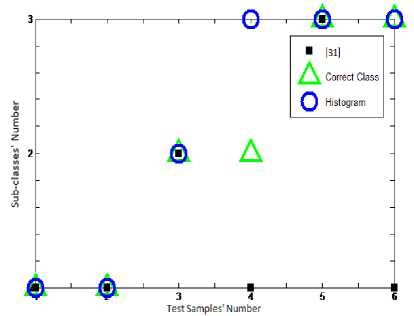
The results of second neural network performance based on NDH are presented below whose aim is recognition of the pertinent sub-classes. Three samples are taken as training and two as test. Due to necessity of brachylogy just classes 10 and 18 are taken as examples to represent the performance of second neural network; hence two mentioned patterns and related NDH are exhibited in figure 10. The vertical axis range is a set of finite values which is equal to unit in the far most point of boundary relative the reference point and is zero in the reference point. The boundary points are depicted versus some optional portions defaulted on ten. Neural network recognition procedure for class ten in training parts shows no error and percentage of test samples interpretation has obtained 83.3 percent. Also in class eighteen the network has reached 100% currency in both training and test parts. Since, images are geometrically so closed and comparable and belong to the one identical category, these results live up to a satisfactory answer of classification.

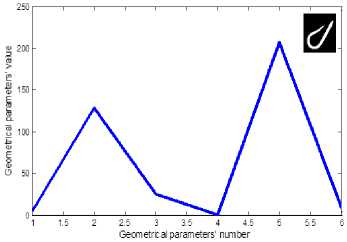
Continuously, the algorithm utilized in reference [31] is applied here and compared with NDH algorithm. Four fundamental parameters consist of six geometric characteristic, D the maximum distance of gravity center, d the minimum distance of gravity center and a the area of the image, are extracted. The image processing based is utilized here to find the geometric parameters. Six DGMs are defined as the feature extractions of second neural network based on [14] as below:

s         s         D         a         a 3a n = - s r2 = - . r3 = - , r4 = — , = — and r6= —

• 1    D "   - d "   j d " 4 D2 ’  b d2b

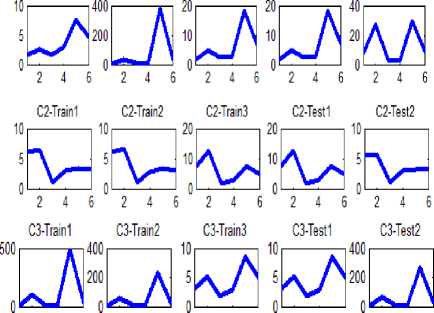
In figure11 the feature extraction vectors of both classes 10 and 18, six dimensionless characteristic, are continually plotted in six horizontal portions. To have a thorough view on the two different feature extractions, the all subsamples of classes 8 and 10 are drawn subsequently. Hence the output of both NDH and DGM approaches are represented by figures 12 and 13, and figures 14 and 15, respectively. Each main class is divided into three sub classes; relevant feature extractions are illustrated in the right side of figures. Accordingly, both algorithm of extracting features are scrutinized to assess the second step performance regarding distinguishing sub-groups. The classification output indicating the correct classes and network prediction based on the two different feature extractions are demonstrated in figures16 and 17. When the distinguished classes lay on the correct ones, it means that network has preciously functioned; considering this fact, the neural network has performed better utilizing NDH approach. In the class ten the correct recognition percentage of both train samples and test samples are 100 percent that has improved by 33.3 % in comparison with the DGM approach by which 66.6 percent in sub-classes recognition is obtained. Correct recognition percentage of testing network in class 18 is concluded in 100% and 83.3% by methods based on NDH and DGM, respectively. Considering all of the classes, general currency of 73% obtained from DGM is superseded by the average of 87% acquired by NDH approach. Not only has this classification algorithm shown a good performance on the first stage of classification, but also the network has presented a reliable recognition of subsamples. The average of 87% is a reliable estimation rate in image interpretation regarding homogeneous samples in different sub-classes of a category. The introduced intelligent recognition has proved to be an effective tool in the purposes of automatic pattern interpretation, especially in which the target accessibility is hard for man. The PNN based on NDH compiles the feature extraction of image samples in two steps, each of which deals with image processing, interpretation, classification and recognizes the most relevant category of pattern. This can facilitate the recognition and observation of critical parts of sub-water structures by ROVs at the least time without any labor and also help firefighter to recognize victims based on body patterns and rescue them before it is too late.

• V.    Conclusion

The whole procedure of neural network performance, which categorizes the images samples, is under investigation in this article. First, the input images are read in the first neural network’s step and the feature extractions, NDHs, are derived and then the fundamental classes of images are determined. Going through a more specified classification imposes another neural network which is applied to classify the images having more anonymous features under sub categories, so the fundamental classes are divided into a number of subclasses. Classification is accomplished based on the recommended method as normalized histogram of boundary points, and the extraction of geometrical factors based on [31]. The results proved that not only this method could be compared with other approaches such [31] withal due to simplicity and even more accuracy in recognition of complex patterns, presents a more thorough solution in classification issues. Authors suggest applying this method experimentally in the operational conditions of ROVs as a future work; In addition to applying it in surgical jobs and tumor - tracking in the body, and firefighting and rescue missions as well. Smart image interpretation provides a viable application in such intelligent devices as robots to accomplish industrial missions as welding, passing obstacle, finding oil and inserting pipelines.

Fig. 1. Some Samples of patterns used as input of neural network

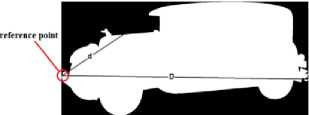
Fig 3. Distances of a sample’s boundary points relative to a reference point

Fig 4. The process of reading the boundary points’ coordinates and distances in an image sample (left to right)

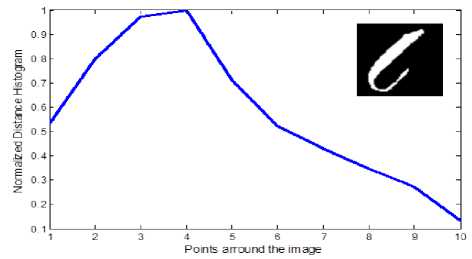
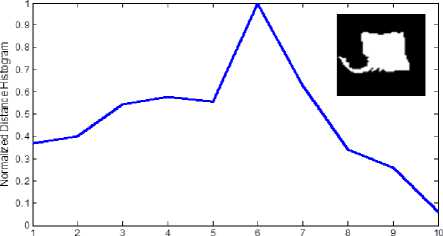
Points around the image

Fig 5. Two different classes of Images and their relevant NDH

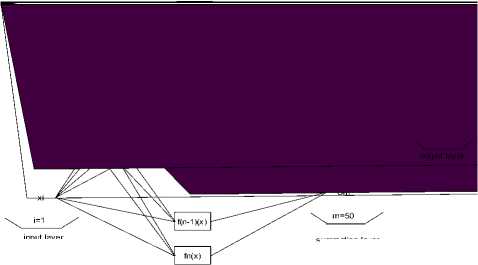
input layer summation layer hidden layer

Fig 2. Architecture of Probabilistic neural network (PNN)

C19-Train1 C19-Train2 C19-Tram3 C19-Train4 C19-Train5

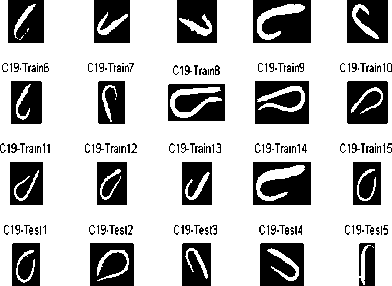
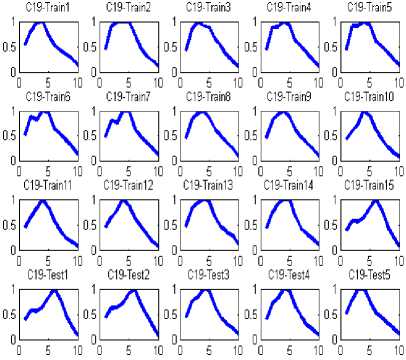
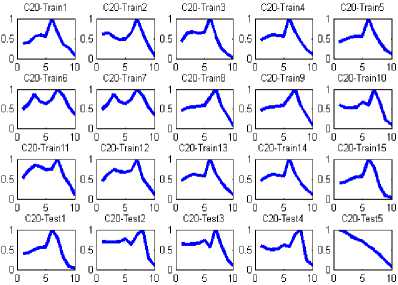
Fig 6. Images and their relevant NDH

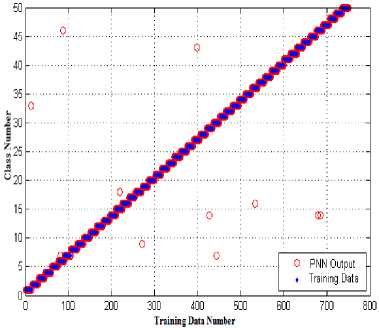
Fig 7. The first neural network performance in training samples’ classification

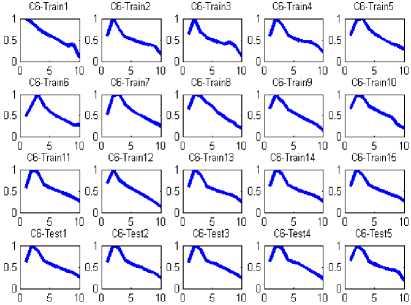
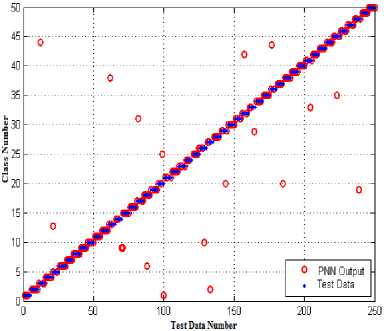
Fig 8. The first neural network performance in test samples’ classification

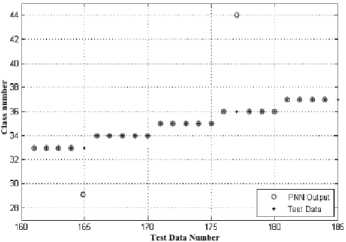
Fig. 9. Snap shot of the first neural network performance in test samples’ classification (class number domain of 33 to 37)

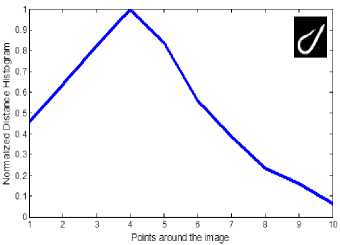
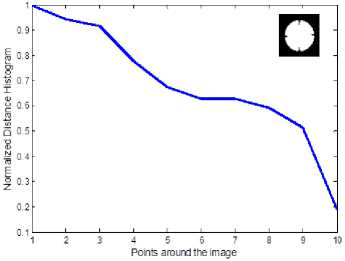
Fig. 10. The normalized distance histograms relevant to the drawn patterns (first: class10 and second: class18)

C1-Train1 C1-Train2 C1-Train3 C1-Test' C1-Test2

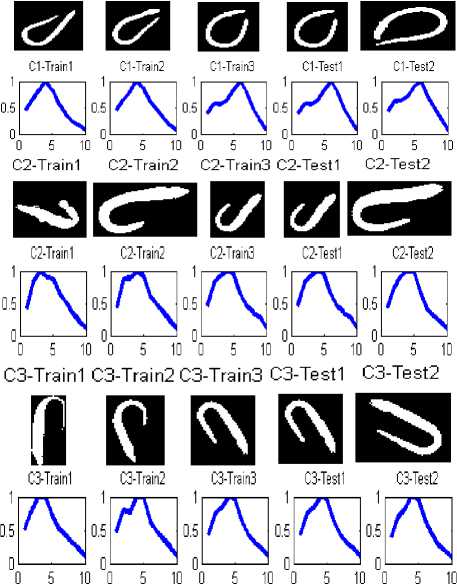
Fig. 12. The NDHs of sub-samples of class 10

C1-Train1 C1-Train2C1-Train3 C1-Test1 C1-Test2

C1-Trainl C1-Train2 C1-Train3 C1-Test1 C1-Test2

C2-Train1 C2-Train2C2-Train3C2-Test1 C2-Test2

□□□□□

C2-Trainl C2-Train2 C2-Train3 C2-Test1 C2-Test2

0     5 10 0     5 10 0     5 10 0     5 10 0     5 10

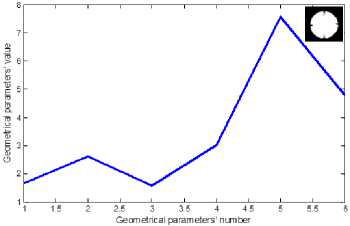
Fig. 11. The Geometric characteristic [31] relevant to the drawn patterns (first: class10 and second: class18).

C3-Train1 C3-Train2C3-Train3C3-Test1 C3-Test2

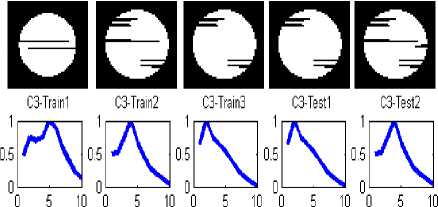
Fig. 13. The NDHs of sub-samples of class 18

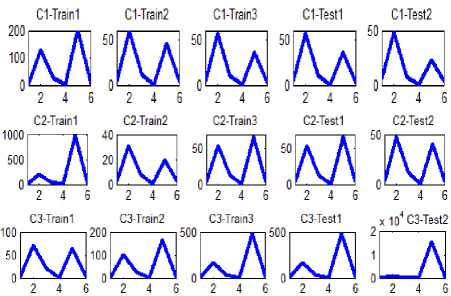
Fig. 14. Six DGMs of sub-samples of class 10

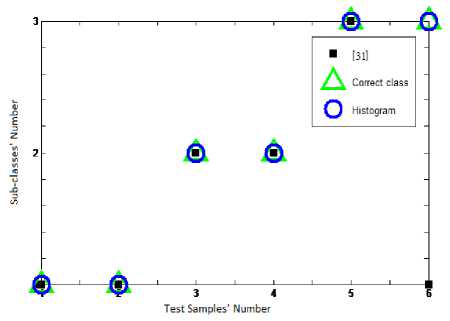
Fig. 17. Sub-samples’ classification of testing samples in second neural network (first: class10. second: class18)

C1-Train1 C1-Train2 C1-Train3 C1-Test1 C1-Test2

2 4 6      2 4 6      2 4 6      2 4 6      2 4 6

Fig 15. Six DGMs of sub-samples of class 18

• [1]    Ou, G. and Y.L. Murphey, Multi-class pattern classification using neural networks. Pattern Recognition, 2007. 40 (1): p. 4-18.

• [2]    Chen, L., W. Xue, and N. Tokuda, Classification of 2dimensional array patterns: Assembling many small neural networks is better than using a large one. Neural Networks, 2010. 23 (6): p. 770-781.

• [3]    Cruz, J., et al., Stereo matching technique based on the perceptron criterion function. Pattern recognition letters, 1995. 16 (9): p. 933-944.

• [4]    Glass, J.O. and W.E. Reddick, Hybrid artificial neural network segmentation and classification of dynamic contrast-enhanced MR imaging (DEMRI) of osteosarcoma. Magnetic resonance imaging, 1998. 16 (9): p. 1075-1083.

• [5]    Lampinen, J. and E. Oja, Distortion tolerant pattern recognition based on self-organizing feature extraction. Neural Networks, IEEE Transactions on, 1995. 6 (3): p. 539-547.

• [6]    Shustorovich, A., A subspace projection approach to feature extraction: the two-dimensional Gabor transform for character recognition. Neural Networks :(8)7 .1994 ,p. 1295-1301.

• [7]    Kepuska, V.Z. and S.O. Mason, A hierarchical neural network system for signalized point recognition in aerial photographs. Photogrammetric engineering and remote sensing, 1995. 61 (7): p. 917-925.

• [8]    Suganthan, P. and H. Yan ,Recognition of handprinted Chinese characters by constrained graph matching. Image and Vision Computing, 1998. 16 (3): p. 191-201.

• [9]    Fukumi, M., S. Omatu, and Y. Nishikawa, Rotationinvariant neural pattern recognition system estimating a rotation angle .Neural Networks, IEEE Transactions on, 1997. 8 (3): p. 568-581.

• [10]    Patel, D., E. Davies, and I. Hnnah, The use of convolution operators for detecting contaminants in food images. Pattern Recognition, 1996. 29 (6): p. 1019-1029.

• [11]    Williams, C.K.I., M.  Revow,  and  G.E. Hinton,

  Instantiating deformable models with a neural net. Computer vision and image understanding, 1997. 68 (1): p. 120-126.

• [12]    Jiang, X. and A. Harvey Kam Siew Wah, Constructing and training feed-forward neural networks for pattern classification. Pattern Recognition, 2003. 36 (4): p. 853867.

• [13]    Aizenberg, I., et al., Cellular neural networks and computational intelligence in medical image processing. Image and Vision Computing, 2001. 19 (4): p. 177-183.

• [14]    Thamarai Selvi, S., S. Arumugam ,and L. Ganesan, BIONET: an artificial neural network model for diagnosis of diseases. Pattern recognition letters, 2000. 21 (8): p. 721-740.

• [15]    Ölmez, T. and Z. Dokur, Classification of heart sounds using an artificial neural network. Pattern recognition letters, 2003. 24 (1): p. 617-629.

• [16]    Zhao, Z.-Q., D.-S. Huang, and B.-Y. Sun, Human face recognition based on multi-features using neural networks committee. Pattern recognition letters, 2004. 25 (12): p. 1351-1358.

• [17]    Meesad, P. and G.G. Yen, Pattern classification by a neurofuzzy network: application to vibration monitoring. ISA transactions, 2000. 39 (3): p. 293-308.

• [18]    Li, Y., et al., Learning-induced pattern classification in a chaotic neural network. Physics Letters A, 2011.

• [19]    Vapnik, V.N., An overview of statistical learning theory. Neural Networks, IEEE Transactions on, 1999. 10 (5): p. 988-999.

• [20]    Vapnik, V., The nature of statistical learning theory1999: springer.

• [21]    Liao, Y., S.C. Fang, and H. LW Nuttle, A neural network model with bounded-weights for pattern classification. Computers & Operations Research, 2004. 31 (9): p. 14111426.

• [22]    Jin, Q., Y. Huang, and N. Fan, Learning images using compositional pattern-producing neural networks for source camera identification and digital demographic diagnosis. Pattern recognition letters, 2012. 33 (4): p. 381396.

• [23]    De Carvalho, A., M. Fairhurst, and D. Bisset, An integrated Boolean neural network for pattern classification. Pattern recognition letters, 1994. 15 (8): p. 807-813.

• [24]    Bacauskiene ,M. and A. Verikas, Selecting salient features for classification based on neural network committees. Pattern recognition letters, 2004. 25 (16): p. 1879-1891.

• [25]    Takano, M., et al., A note on a higher-order neural network for distortion invariant pattern recognition. Pattern recognition letters, 1994. 15 (6): p. 631-635.

• [26]    Verikas, A. and M. Bacauskiene, Feature selection with neural networks. Pattern recognition letters, 2002. 23 (11): p. 1323-1335.

• [27]    Wang, Y., et al., Feature selection using tabu search with long-term memories and probabilistic neural networks. Pattern recognition letters, 2009. 30 (7): p. 661-670.

• [28]    Meyer-Bäse, A. and R. Watzel, Transformation radial basis neural network for relevant feature selection. Pattern recognition letters, 1 :(14)19 .998p. 1301-1306.

• [29]    Bruzzone, L. and S. Serpico, Classification of imbalanced remote-sensing data by neural networks. Pattern recognition letters, 1997. 18 (11): p. 1323-1328.

• [30]    Nadir Kurnaz, M., Z. Dokur, and T. Ölmez, Segmentation of remote-sensing images by incremental neural network. Pattern recognition letters, 2005. 26 (8): p. 1096-1104.

• [31]    Lin, C.-Y. and S.-H. Lin, Artificial neural network based hole image interpretation techniques for integrated topology and shape optimization. Computer Methods in Applied Mechanics and Engineering, 2005. 194 (36): p. 3817-3837.

• [32]    Li, Y., et al., Learning-induced pattern classification in a chaotic neural network. Physics Letters A, 2012. 376 (4): p. 412-417.

• [33]    Paliwal, M. and U.A. Kumar, Neural networks and statistical techniques: A review of applications. Expert Systems with Applications, 2009. 36 (1): p. 2-17.

• [34]    Yu, D. and L. Deng, Efficient and effective algorithms for training single-hidden-layer neural networks. Pattern recognition letters, 20 :(5)33 .12p. 554-558.

Authers' Profiles

Sogand Hoshyramanesh holds a master of mechanical engineering from Amirkabir University of Technology and is a researcher at robotic lab. Her particular areas of expertise are computational simulations, Nanosensors and Nanotechnology.

Mohammadreza Fathi Kazerooni holds bachelor of naval architecture from Amirkabir University of Technology and master of ship hydrodynamics from Sharif University of Technology and is currently a doctoral student in marine engineering at Sharif University of Technology and technical director of marine engineering lab. His particular areas of expertise are marine hydrodynamics, dynamics of marine vehicles and ship maneuvering.

Mohsen Bahrami holds a PhD of mechanical engineering from Oregon state university. Professor Mohsen Bahrami is a fuculty member and Robotic Laboratory head in mechanical engineering department, Amirkabir University of Technology. His areas of expertise are robot dynamics and control application, flight dynamics and control, satellite dynamics and control.