Интерактивные средства специализации программ

Понятие специализации. Специализация — это оптимизация программ под определенные условия ее выполнения. Такими условиями могут быть конкретные значения некоторых из ее входных данных или, например, целевая архитектура системы, на которой предполагается выполнять программу.

Более формально, рассмотрим программу f : X, Y ^ Z , принимающую на вход два аргумента x и y . Пусть значение одного из ее аргументов x известно и равно a.

Тогда результатом специализации программы f по известному аргументу x = а называется новая программа от одного аргумента g : Y ^ Z , обладающая следующим свойством: f (a, y) = g(y) для любого y.

Отметим, что известное значение a, по которому выполняется специализация, не обязательно должно быть числовой константой. Аргумент a может быть содержимым файла или даже сущностью высшего порядка, например, некоторым набором функций. То есть a отражает условия, к которым адаптируется исходная программа.

Частичные вычисления — это один из методов специализации программ. Существует два подхода к частичным вычислениям — онлайн и оффлайн.

Онлайн вариант выполняет только один проход по специализируемой программе. Решения о преобразовании той или иной конструкции принимается на основе неполной (локальной) информации и эти преобразования сразу же выполняются.

Оффлайн вариант частичных вычислений выполняется в два этапа: сначала собирается глобальная информация о программе и временах связывания конструкций, а потом происходят преобразования.

В оффлайн частичных вычислениях первый этап является анализом времен связывания (binding-time analysis, BTA), и на этом этапе конструкции специализируемой программы разделяются на статические (зависящие от известных данных, S-конструкции) и динамические (зависящие от неизвестных данных, D-конструкции).

На втором этапе оффлайн частичных вычислений — генерации остаточной программы — операции над S-конструкциями выполняются, а D-конструкции переходят в результирующую (остаточную) программу.

Для реализации выбран метод оффлайн частичных вычислений. Такое решения обусловлено тем, что частичные вычисления лучше, чем другие методы специализации (например, суперкомпиляция), подходят для реализации человеко-машинного диалога, организованного таким образом, чтобы пользователь понимал, что происходит в специализаторе, получал ценную и интересную информацию о коде, был способен корректировать исходный код для лучшей специализации и управлял специализатором.

История частичных вычислений. Впервые специализацию начали исследовать около 40 лет назад. Одним из первых специализаторов был MIX [1] . MIX является первым инструментом, который доказал на практике возможность генерации компиляторов с помощью частичных вычислений. Этот научный результат стимулировал дальнейшее развитие методов специализации программ.

Следующим значимым специализатором является C-MIX [2 , 3] Этот специализатор был разработан в начале 1990-х годов. Существенным продвижением было добавление анализа указателей и анализа побочных эффектов. Эти два анализа наряду с BTA позволили применить частичные вычисления к языку программирования C, интенсивно использующему указатели. До C-MIX специализацию применяли к функциональным программам, а широко используемые императивные языки оставались вне области частичных вычислений.

Другим частичным вычислителем работающим с подмножеством языка C является Tempo [4 , 5] . Во многом Tempo похож на C-MIX, он использует анализ синонимов и определений для решения проблем указателей в языке C. Существенным достижением Tempo является то, что его применили к реальным программам. Tempo использовался для оптимизации функций marshaling (упаковки) данных в библиотеке XDR в составе Remote Procedure Call (RPC) компании Sun.

В 2001 году У. П. Шульц разработал специализатор JSpec для объектно-ориентированных программ [6 –8] . JSpec основан на трасляции Java в C и последующем применении частичного вычислителя Tempo к программам на С. Это был первый подход к специализации программ на объектно-ориентированных языках.

В 2009 году Ю. А. Климов реализовал частичный вычислитель CILPE. [12 –19] . CILPE применялся к подмножеству объектно-ориентированного языка CIL [20] , байт-коду платформы Microsoft .NET. Важным для нас продвижением было то, что Ю. А Климов придумал многовариантный способ разметки классов, в результате которого была продемонстрирована возможность удаления объектов из программы с разделением их на поля. Такой подход позволяет содержательно специализировать часть объектно-ориентированных программ, добиваясь существенного ускорения.

В конце 2000-х годов Анд. В. Климов опубликовал работы по специа-лизатору JScp [9, 10] на основе метода суперкомпиляции [11] , развив его от функциональных языков на объектно-ориентированные. Хотя ставилась цель довести суперкомпиляцию до практики, но это не удалось: оказалось, что пользоваться им практически невозможно из-за того, что программисту необходимо понимание логики его работы, а JScp был «черным ящиком». Полученный опыт показал, специализатор должен быть погружен в IDE с удобными средствами управления, для чего потребуется его переработка, и суперкомпиляция слишком сложна для первых практических специализаторов.

За первые 30 лет развития специализация программ так и не получила широкого распространения, а практические применения не носили массовый характер. Однако сам метод развивался и был накоплен большой научный опыт.

Современное состояние. В последние годы стали появляется примеры практического использования частичных вычислений. В первую очередь необходимо упомянуть фреймворк Truffle, входящий в набор инструментов GraalVM [21, 22] , который сейчас принадлежит Oracle. Truffle позиционируется как инструмент для эффективной и простой реализации предметно-ориентированных языков (DSL). В основе GraalVM лежит онлайн частичный вычислитель. Простота обеспечивает высокую скорость работы самого специализатора, которая является критической для этого инструмента, поскольку преобразования программ осуществляются на этапе исполнения, во время работы JIT-компилятора. Тем не менее, при всех усилиях существенная часть (до 73%) времени JIT-компиляции тратится на специализацию [23] . Требуется отметить, что методология Oracle не распространилась широко.

Еще одна современная система, основанная на частичных вычислений, — AnyDSL [24] , — представляет собой систему программирования, основанную на частичных вычислениях. AnyDSL позволяет получать высокопроизводительные реализации для CPU (с векторизацией и распараллеливанием) и GPU из единой кодовой базы на едином языке. Производительность сгенерированного кода составляет преимущественно в пределах 10% (иногда ближе) от производительности многолетних, вручную оптимизированных экспертных кодов промышленного уровня, которые считаются лучшими в своих областях. При этом усилий, затрачиваемых на реализацию библиотек на AnyDSL, существенно меньше.

Примерами реализаций высокопроизводительных библиотек на AnyDSL являются AnySeq [25], Rodent [26] и AnyHLS [27]. В AnySeq решается задача выравнивания последовательностей ДНК, Rodent нацелен на рендеренг сцен в компьютерной анимации, а AnyHLS использует частичные вычисления для синтеза дизайнов FPGA модульным и абстрактным способом. Все три библиотеки основываются на идеологии AnyDSL, в которой алгоритм разделяется на две части: общую часть и часть, предназначенную для оптимизации под различные архитектуры. Применение частичных вычислений позволяет эффективно удалить накладные расходы, возникающие из-за использования высокоуровневых абстракций.

Существует язык программирования, который основывается на специализации — язык Julia [28] . Стратегия компиляции Julia построена на информации о типах, доступной во время выполнения. Каждый раз, когда метод вызывается с новой комбинацией типов аргументов, он специализируется под эти типы. Оптимизация методов в момент вызова, а не заранее, предоставляет JIT-компилятору ключевую информацию: расположение в памяти всех аргументов известно, что позволяет распаковывать объекты и напрямую обращаться к полям. Специализация, в свою очередь, позволяет девиртуализировать методы. Такой подход позволяет Julia, как и AnyDSL, генерировать реализации одной и той же программы под разные архитектуры (x86, GPU или FPGA).

В 2025 году был представлен новый специализатор weval [29] . Специа-лизатор weval работает только с wasm байткодом, предназначенным для исполнения в браузере. В wasm нет объектов. Память имеет линейную структуру в виде массива целых чисел. За линеаризацию объектов отвечает компилятор из высокоуровневого языка в wasm. Существует несколько фронтендов, компилирующих C, C++ и даже Java в wasm.

Основным назначением weval является оптимизация и сплющивание цикла интерпретации. Weval существенно закладывается на определенный стиль реализации интерпретаторов — switch-case по типам узлов в Control Flow Graph. Тип узла представляется в виде opcode — целой переменной. Авторами weval утверждается, что «вылизанные» промышленные интерпретаторы из-за необходимой эффективности применяют именно такой способ взаимодействия с узлами графа программы. Weval — это онлайн специализатор, основанный на относительно простой теории, но удачно примененный в месте, где эта теория эффективно работает на практике.

Резюме. Мы считаем, что причиной ограниченного практического применения специализации является то, что авторы ориентировали свои инструменты на применение в «черно-ящичном» режиме [30]. Задача специализации программ обладают слишком многими степенями свободы, поэтому она не может быть решена с помощью полностью автоматических алгоритмов и, следовательно, помощь со стороны человека-пользователя является необходимой для применения специализаторов на практике.

Все представленные выше современные инструменты не используют полную силу специализации. В перечисленных практических системах всегда выбирался онлайн вариант, преобразования в котором основываются на локальной информации. Причиной такого выбора является нерешенная задача управления сложным оффлайн подходом к частичным вычислениям.

Сложности при применении частичных вычислений заключается в том, что зачастую первый подход к программе не дает желаемой степени оптимизаций. При этом проблема которая ограничивает преобразования проявляется в одном месте, а возникает в другом. Чтобы соотнести источник проблемы с местом ее проявления, приходится либо переписывать программу, либо изучать работу специализатора отладчиком. Оба решения требуют много времени на устранение всего одной проблемы. На программах реального размера проблем может быть несколько десятков и на специализацию таких программ уходит неприемлемое количество сил и времени.

Оффлайн частичные вычисления отличаются тем, что предоставляют естественный разрез, который является планом преобразований. Этот план хорошо визуализируется и содержит большой объем ценной информации о программе и ее специализации, благодаря чему программист лучше понимает происходящие преобразования.

Предлагаемое решение.

• ^•    Для того, чтобы пользователь понимал, почему получен тот или иной результат, метод специализации должен работать с представлениями программы близкими к исходному коду. Предыдущие системы работали с внутренним кодом из элементарных операций для теоретической простоты.

• ^•    В качестве метода специализации выбраны оффлайн частичные вычисления, поскольку они основаны на естественном разрезе между анализом времен связывания и последующей генерацией остаточной программы. Такой подход позволяет дать пользователю промежуточную информацию о работе алгоритма специализации. В свою очередь в силу естественности разреза пользователь на основе промежуточной информации намного лучше понимает, как и почему применены те или иные преобразования.

• ^•    Результаты первого прохода по программе — BTA — тем не менее, достаточно сложны для понимания, поэтому нужны дополнительные средства. В качестве таких средств в настоящей статье описываются подсветка результатов BTA и история причин BT-разметки. История причин BT-разметки является новой идеей, разработанной и реализованной впервые.

Ранее автором разработан и реализован специализатор JaSpe [31 –36] . Первый опыт его применения показывает, что подход на основе оффлайн частичных вычислений ускоряет интерпретаторы в 10-30 раз, фактически компилируя интерпретируемую программу в Java.

Структура статьи. Далее изложение имеет следующую структуру. В разделе 1 частичные вычисления описываются с точки зрения применяемых преобразований. Раздел 2 иллюстрирует работу анализа времен связывания на простом примере. В разделе 3 более детально рассматривается интерактивная специализация с точки зрения проблем классических частичных вычислений. Раздел 4 посвящен новому решению проблем частичных вычислений. Технологии, на основе которых разработан новый специализатор, описаны в разделе 5 . В разделе 6 описывается классический алгоритм BTA. Раздел 7 рассказывает о визуализации результатов BTA в виде подсветки кода. Затем в разделе 8 приводится базовый сценарий работы со специализатором на основе подсветки кода. Раздел 9 посвящен идеям истории причин BT-разметки — дополнительному интерактивному средству, существенно ускоряющему и упрощающему процесс достижения успешной специализации. В разделе 10 приводится пример иллюстрирующий принципы работы истории причин BT-разметки. В разделе 11 — идеи фильтрации причин. В разделе 12 описывается типовой сценарий взаимодействия со специализатором с использованием истории причин BT-разметки. И, наконец, раздел «Заключение» подводит итоги.

1.    Оптимизирующие преобразования частичных вычислений

Частичные вычисления дают единую схему для применения преобразований, которые в других методах выполняются отдельными правилами. Также частичные вычисления характеризуются агрессивными методами распространения констант и преобразованиями, связанными с таким распространением.

Р. Марле в своей работе [5] провел следующие параллели между частичными вычислениями и аналогичными преобразованиями в других методах. Кратко опишем суть этих преобразований.

Function unfolding подставляет телo функции в местах ее вызова.

Иногда это преобразование называют inlining .

Function folding обнаруживает похожие участки кода в программе и выносит их в отдельное определение функции. Сами участки при этом заменяются на вызовы этой функции. Это обратное преобразование по отношению к function unfolding.

function redefinition означает добавление новых определений функций на основе уже существующих, например с меньшим числом аргументов.

Constant-propagation распространяет константы по программе, подставляя значения констант вместо их имен.

Constant expression evaluation вычисляет значения выражений, основанных только на константах. Например вместо сложения двух констант подставляет значение их суммы.

Algebraic simplification упрощает арифметические выражения. Это особенно актуально, когда часть выражения было вычислена другими преобразованиями.

Conditional expression resolution подставляет что когда известные значения условий в if, switch и прочих условных конструкциях, оставляя вместо всей конструкции только одну ветку, выбранную на основе значения условия.

Loop unrol ling разворачивает цикл когда известно число его итераций. Число итераций может быть вычислено на основе других оптимизаций частичных вычислений.

Ю. А. Климов добавил [12 –19] к ним еще одно преобразование, важное для объектно-ориентированных программ, — это object elimination . Суть этого преобразования заключается в том, что при некоторых условиях возможно удаление объекта и которые представляют часть полей этого объекта и всех операций с ним из программы. При этом преобразовании объект заменяется на локальные переменные, операции над которыми невозможно выполнять на этапе компиляции из-за их зависимости от неизвестных данных.

Оптимизация ob ject elimination актуальна для объектно-ориентированных программ. Успешное применение других оптимизаций в рамках объектно-ориентированной парадигмы во многом зависит от того, удалось ли преобразовать объекты в привычные для классических частичных вычислений переменные примитивных типов или массивы.

2.    Пример специализации простой программы методом частичных вычислений

На рисунке 1 слева изображена размеченная исходная программа, а справа результат ее преобразования нашим специализатором.

@Specialize public static int example(int dArgument) { int a = 5;

int result = 0;

boolean myTrue = true ;

if (!myTrue) { result = sum(dArgument, a);

} else { result = sum(a, 2);

} result = result * 2;

return result ;

} public static int sum(int a, int b) { return a + b;

}

Легенда:

S      D■ I  M■

public static int example_Spec(int dArgument) { int ret_sum;

int result;

ret_sum = sum_5_2 ();

result = ret_sum;

result = result * 2;

return result;

} public static int sum_5_2() { return 7;

}

Рисунок 1. Пример размеченной исходной программы и результата ее специализации.

Исходная программа — «дурацкая» и не имеет никакого практического смысла, она составлена только для иллюстрации принципов работы специализатора.

Разметка программы происходит на первом этапе частичных вычислений — анализе времен связывания (BTA). Для удобства пользователя разметка программы визуализируется специализатором — это позволяет понять, какие конструкции были оптимизированы, а какие нет. Визуализация разметки — это одно из решений, разработанных в рамках настоящей работы (раздел 7 ниже).

Зеленым цветом изображены конструкции, которые будут подвергнуты преобразованиям — S-конструкции (известные), а синим те, что перейдут в результирующую (остаточную) программу — D-конструкции (неизвестные). Коричневым цветом подсвечены M-конструкции, которые на одном пути анализа S, а на другом D.

Рассмотрим то, как BTA планирует преобразования, которые будут выполнены генератором остаточной программы. Анализ программы начинается со входной точки – это метод example, поскольку он помечен аннотацией @Specialize. Аргумент такого метода может принимать произвольные и потому неизвестные специализатору значения. Исходя из этого факта, аргумент метода example — dArgument — размечается как D.

Далее анализ заходит в тело метода example и видит, что переменным a , result и myTrue присваиваются заранее известные значения. Значит, на основе знания об этих значениях можно будет вычислить другие выражения. Поэтому специализатор размечает переменные a , result и myTrue S-разметкой.

Алгоритм BTA размечает if и его условие как S, поскольку они основываются на известном S-значении и к ним можно применить преобразование conditional expression resolution. Далее анализ заходит в ветку then, несмотря на то, что эта ветка никогда не будет исполнена. Такое поведение связано с тем, что BTA оперирует абстрактными понятиями «известно/неизвестно» (S/D), а не конкретными числовыми или логическими значениями. Соответственно, анализ не может понять истинно ли условие или ложно, ему известно только то, что на этапе генерации программы будет выбрана какая-то конкретная ветвь, но BTA не может определить какая.

Посещая ветвь then, BTA понимает, что вызов метода sum можно соптимизировать, так как один из его аргументов известен, а второй нет. Анализ посещает тело метода sum и размечает все конструкции, кроме тех, которые полностью определяются аргументом b , D-разметкой. Именно с этим связан коричневый цвет — это M-конструкции, на первом посещении return , a и + имеют D-разметку, а на следующем — S. Чтобы визуализировать тот факт, что при разных посещениях конструкции имеют различную разметку, был использован коричневый цвет.

После анализа then ветки, BTA переходит к анализу else. В ветке else также вызывается метод sum . Но у него два известных аргумента. BTA понимает, что тут можно применить преобразование function redefinition — будет сгенерирована новая версия метода sum , которая не содержит аргументов (поскольку они известны).

Перед завершением анализа конструкции if , BTA выполняет слияние разметок переменных, полученных на обеих ветвях. Слияние необходимо, так как BTA не знает какую разметку для переменной result использовать дальше — полученную на ветке then или на ветке else. При слиянии разметки переменных выбирается всегда худшая разметка из имеющихся. То есть переменная result получает D-разметку. На этом анализ условной конструкции if завершается.

После анализа if , BTA переходит к анализу следующих после нее конструкций: присваивание и return . Как мы только что отметили, переменная result размечена D, а все операции над D-переменной тоже D. Поэтому обе конструкции получают D-разметку.

На этом анализ завершается и выполняется генерация остаточной программы, которая уже знает конкретные значения и то, какие конструкции надо вычислить (размеченные как S), а какие перенести в остаточную программу (размеченные как D).

В результате получится остаточная программа, изображенная справа на рисунке 1 . Обратим внимание, что был сгенерирован метод sum_5_2() , который соответствует двум константным аргументам 5 и 2 . Это результат применение преобразования function redefinition. Дополнительно могла быть применено преобразование function unfolding (inlining), в этом случае вместо вызова sum_5_2() была бы константа 7 и программа получилась бы еще более эффективной. Требуется отметить, что решение применять ли то или иное преобразование не всегда так очевидно.

Стоит обратить внимание и на то, что в остаточной программе присутствуют лишние действия — присваивания, связанные с переменной ret_sum , которые можно было бы удалить. В этой части мы полагаемся на JIT-компилятор Java, который, как показывает практика, сделает эту работу за специализатор.

3.    Интерактивные частичные вычисления

С момента публикации первых работ по частичным вычислениям и до настоящего времени прошло более 40 лет, но специализация программ так и не получила широкого распространения [30] . Относительно недавно стали появляться практические успехи простых вариантов частичных вычислений, тем не менее и они не вошли в широкую практику и, что самое главное, все самые мощные методы специализации так и остаются уделом относительно небольшого количества научных групп. В чем же причина?

Одна из самых критических проблем современных частичных вычислений заключается в том, что самые сильные их преобразования сложно применить на практике. Сложность применения обусловлена тем, что специализация программ содержит слишком много степеней свободы и требует существенного вовлечения человека в процесс специализации.

Действительно сильные преобразования часто не приносят пользы, если применены автоматически, а иногда даже могут замедлить программу. Бывает, что необходимо небольшое локальное переписывание кода программы и тогда сильные преобразования срабатывают. Такие переписывания получили специальное название — улучшение времен связывания (binding time improvements). На данном этапе развития частичных вычислений улучшения времен связывания не могут быть выполнены автоматически, поскольку специализатор не знает, что конкретно программист хочет от программы и какова его цель.

Однако, если программист получит от специализатора информацию, в каких местах требуются улучшения времен связывания, то обычно человек вносит такие изменения быстро.

Тем не менее до сих пор не предпринималось целенаправленных попыток упростить взаимодействие специализатора и человека. Поэтому авторы в данной статье хотят показать необходимость интерактивного взаимодействия программиста с системами частичных вычислений и предоставить решения основных проблем, возникающих на этом пути.

Отметим, что сложность применения частичных вычислений создает критические барьеры для масштабирования этого метода на реальные задачи. Однако, частичные вычисления — это один из самых легких методов специализации с точки зрения внедрения интерактивных средств. Причиной такой позиции является то, что частичные вычисления естественно разделены на два этапа — BTA и генерация остаточной программы. Все преобразования определяются результатами BTA и, если выбрать правильный подход к BTA, то его результаты можно понятно визуализировать.

Переход от черно-ящечной специализации к интерактивной сравним с переходом от пары компилятор и текстовый редактор к полноценным графическим IDE. В такие IDE встроено множество инструментов для помощи программисту. Для простого программиста переход к IDE означает значительное повышение продуктивности и комфорта. В случае с частичными вычислениями переход к интерактивным средствам, в том числе к встраиванию в IDE, может дать еще более критичные улучшения в эффективности.

Одна из проблем, которая решается с помощью интерактивности — это постановка задачи на специализацию. Ранее для формирования такого задания требовалось создавать конфигурационные файлы или запускать специализатор с длинными и сложными аргументами. Поэтому специализаторами пользовались в основном их создатели.

Другая проблема: как сообщить пользователю, почему получилась именно такая остаточная программа? Зачастую в процессе специализации принимается множество решений и применяется достаточно много преобразований. Поэтому без специальных средств может быть затруднительно понять связь между исходной и остаточной программами.

Существенной трудностью для частичных вычислений является и то, что проблема, препятствующая преобразованию, часто возникает в одном месте, а проявляется в другом. До данного момента не было разработано эффективных приемов решения задачи соотнесения источника, препятствующего преобразованию, с местом проявления проблемы. Ранее пользователь должен был изучать поведение специализатора с помощью отладчика или переписывать программу чтобы найти источник, который мешает преобразованиям.

4.    Решения для интерактивных частичных вычислений

Далее мы опираемся на метод Ю. А. Климова [12 –19] , который является наиболее развитым для объектно-ориентированных программам. Метод Ю. А. Климова работает с графом потока управления (Control-Flow Graph, CFG) поскольку CFG наиболее удобен для анализа. Однако использование CFG создает проблемы для визуализации результатов анализа на исходном коде программы, который видит пользователь.

Как оказалось, необходима доработка и адаптация основных принципов и алгоритмов. Поэтому здесь предлагаются решения, затрагивающие как основные понятия частичных вычислений, так и конкретные моменты их реализации.

Приведем список изменений в ключевых методах и понятиях частичных вычислений:

• (1 )    Работа BTA и генератора остаточной программы с деревом абстрактного синтеза (Abstract Syntax Tree, AST), а не с CFG. Переход от работы с CFG к работе с AST необходим потому, что AST один в один представляет то, как пользователь видит текст программы на экране. Здесь CFG — это удобное представление для компилятора, поскольку к нему легче применять некоторые преобразования. Соответственно, при переходе от CFG к AST все решения анализа и разметка, которую специализатор строит, становятся намного более понятны пользователю.

Однако перейти от одного представления программы к другому не так просто, если часть методов разметки и оптимизации опирается на определенное представление — в нашем случае CFG. Поэтому эти методы пришлось адаптировать.

• (2)    Переработка алгоритмов BTA, их ориентация на работу на работу с конструкциями «сверху вниз», а не в терминах элементарных операци й 1, как в предыдущих работах [12 –19] .

Переход от алгоритмов работающих на уровне элементарных операций к алгоритмам типа «сверху вниз» необходим, чтобы выдаваемые диагностики были понятны пользователю. Такой переход, помимо прочего, формирует задел на будущее для интерактивных средств сопоставления остаточного кода с исходным.

• (3)    Включение в метод анализа истории причин BT-разметки, чтобы специализатор мог сохранять и визуализировать трассу изменения BT-значений.

История причин BT-разметки позволяет пользователю специа-лизатора быстро находить источники проблем, препятствующих преобразованиям. Поиск таких проблем является критическим местом для масштабирования частичных вычислений на реальные задачи. Более детально об истории причин рассазанно далее в разделе 9.

В дополнение пришлось перейти к новым определением базовых понятий:

• (4)    Доработка формального определения BT-значения и переработка понятия BT-объекта. Новые определения учитывают идеи истории причин BT-разметки, а также создают более удобную формальную теорию.

5.    Реализация методов интерактивных частичных вычислений

Обновлённая теория позволила специализатору визуализировать трассу изменения BT-значений. Подробнее об этом в разделе 9 ниже.

Все эти изменения внесены с целью создания основания для полезных интерактивных средств и их поддержки в IDE, а также для масштабирования частичных вычислений во всей их силе на реальные задачи.

Интерактивный специализатор JaSpe [31 –36] погружен в привычную программистам интегрированную среду разработки (IDE) Eclipse.

Была поставлена задача реализовать методы частичных вычислений так, чтобы они масштабировались на применение к реальным программам. Объектно-ориентированный язык программирования Java выбран в качестве языка программы на котором должен специализировать JaSpe, по следующим причинам:

• ^•    Нет явных указателей и их арифметики, что упрощает анализ.

• ^•    Автоматизация работы с памятью и сборка мусора.

• ^•    Статическая типизация, которую эксплуатирует наш специализатор.

• ^•    Java архитектурно независим, используется на большом числе устройств.

• ^•    Высокая эффективность за счет компиляции в байт-код и применения JIT. На большом числе мобильных платформ возможна непосредственная компиляция в машинный код (для Android используется компилятор ART).

• ^•    Есть IDE с доступом к AST Java-программ и возможностью встраивания специализатора в IDE.

• ^•    Java широко распространен, много программистов работающих на этом языке, а значит больше вероятность найти заинтересованную аудиторию.

6.    Обьяснение BTA

Специализатор встроен в мощную, признанную программистами среду графической разработки Eclipse IDE. Иногда Eclipse критикуют за «монструозность» и «тяжеловесность», но нам ценны эти особенности. Разобравшись с API этой системы, мы получаем доступ к уже готовым решениям, а значит снимаем с себя нагрузку по реализации части необходимой нам функциональности.

Особенно важным для нас компонентом Eclipse IDE является Java Development Tools (JDT). Это набор инструментов, который включает в себя лексический и синтаксический анализаторы, проверку и связывание типов. JDT для каждого выражения вычисляет его статический тип и предоставляет средства поиска определений типов и навигации по коду в целом.

Синтаксис в JDT представляется в виде AST, что крайне удобно для реализации нашего подхода. Чтобы обойти это дерево, JDT предполагает использование широко известного шаблона «посетитель» (Visitor pattern) [37] .

Отметим, что развиваемые здесь методы интерактивной специализации, переносимы на любую другую IDE с аналогичным набором инструментов.

Алгоритм BTA основан на абстрактной интерпретации. При старте BTA начинает исполнять программу во многом аналогично интерпретатору. Однако вместо оперирования числовыми, логическими, символьными и прочими конкретными значениями, BTA интерпретирует выражения в форме «известно» или «неизвестно». Например числовая константа «5» считается известной, а переменная, которая является аргументом программы, — неизвестной.

Понятия «известно»/«неизвестно» выражены в BTA в виде BT-значений S или D соответственно.

Значение undefined означает, что выражение или инструкция еще не получило разметку. Разметка S означает, что значение выражения известно, оно будет вычислено и отсутствует в остаточной программе. Разметка D означает, что выражение зависит от неизвестных на этапе специализации данных и специализатор не может вычислить это выражение, а значит оно перейдет в остаточную программу. BT-значение инструкций и выражений примитивных типов в процессе разметки программы, может только увеличивается в соответствии с отношением порядка в решетке { undefined, S, D } , где undefined < S < D. Аналогично с инструкциями.

Переменные и выражения, чей тип описывается классами, получают в качестве разметки BT-объект. BT-объект — это вариант разметки класса.

BT-объект содержит разметку каждого поля класса и разметку верхнего уровня, которая определяет нужно ли применять оптимизацию object elemination .

Анализ программы начинается с метода, отмеченного как точка входа в специализацию (specialization entry point). Для обозначения точки входа в специализацию мы используем java-аннотацию @Specialize . В остаточном коде этот метод будет замещен на его специализированную, функционально эквивалентную версию.

Аргументы точки входа получают D-разметку. BTA последовательно «абстрактно интерпретирует» программу, начиная с точки входа. BTA обходит вложенные инструкции и подвыражения, которым также присваю-ваются значения S или D по определенным правилам. После абстрактной интерпретации инструкции BTA переходит к следующей почти как и при обычной интерпретации. Однако во время такой интерпретации возможны откаты к уже проанализированным конструкциям из-за изменения глобальной информации (подробнее об этом можно прочитать в [33] ).

Несколько путей вычислений, по которым BTA приходит к той или иной конструкции, и откаты анализа существенно затрудняют понимание человеком результатов специализации.

7.    Визуализация разметки программы

BTA строит разметку программы и размечает переменные и конструкции как S или D. Это информация используется второй фазой специализатора — генератором остаточной программы как инструкции, что делать: исполняться S-код или переносить D-код в остаточную программу. Но она ценна и разработчику программы для понимания происходящего в специализаторе и ее полезно сообщать пользователю. Визуализация BT-разметки программы в данном случае является подходящим решением. Конструкции программы раскрашиваются в Java-редакторе внутри Eclipse IDE в соответствии с результатами BTA (как на рисункне 1) .

BTA в специализаторе JaSpe может при разных проходах абстрактной интерпретации давать независимые и разные разметки. Такая ситуация случается в двух случаях:

• (1)    При анализе тела метода: когда один и тот же метод вызывается из разных мест в программе, то для каждого вызова метода может строится отдельная разметка тела этого метода. То есть тело метода и все конструкции в нем могут иметь несколько разметок.

• (2)    BT-объект —это вариант разметки класса. Соответственно, если существует несколько BT-объектов, происходящих из разных вхождений класса в код, то поля этого класса могут иметь несколько разметок (по числу таких BT-объектов).

8.    Типовой сценарий специализации программы

Чтобы показать места, где накладываются несколько вариантов разметок, они «обобщаются» в одну общую итоговую разметку. Обобщения выполняются на основе решетки (см. рисунок 2) . Кратко это обобщение

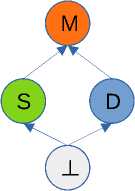
Рисунок 2. Решетка для обобщения раскрасок.

можно описать так: если какая-то конструкция размечена как S и D одновременно, для нее находится верхняя грань — то M-разметка.

По умолчанию JaSpe визуализирует S-разметку зеленым, D — синим, M — коричневым. Цвета и форма разметки могут быть настроены пользователем под себя средствами Eclipse IDE.

В заключение отметим, что из практики трех цветов для подсветки кода достаточно: программисту требуется установить, какое выражение может препятствовать преобразованиям. Проблемное выражение обычно либо D (синее), либо M (коричневое). Далее достаточно запросить историю причин данной разметки и она уже содержит все возможные варианты.

При использовании описанных средств возникает такой сценарий применения специализатора JaSpe:

• (1)    Пользователь применяет специализатор к программе.

• (2)    Пользователь находит в остаточной программе, места, которые не оптимизировались.

• (3)    Пользователь не удовлетворен остаточной программой.

• (4)    Пользователь изучает BT-разметку исходной программы в тех местах, где он ожидал преобразования.

• (5)    Программист ожидал S, а получил D в ключевом на его взгляд месте и хочет понять, почему.

• (6)    Пользователь размышляет над причинами, которые препятствуют ожидаемым преобразованиями и изменяет программу в соответствии со своими выводами.

• (7)    Эта процедура выполняется итеративно начиная с шага 1 до тех пор, пока пользователь не будет удовлетворен результатом.

9.    Базовые понятия истории причин BT-разметки

Отметим, что пункт (6) в случае с реальными программами требует существенных умственных усилий и много времени. Программист видит код, который размечен как D, там где он ожидал S. Однако найти источник проблемы часто бывает затруднительно: обычно источник проблемы и ее проявление существенно разнесены в программе. Ситуацию осложняет и тот факт, что не всегда понятны пути, по которым BTA пришел к той или иной точке, а также откаты в процессе абстрактной интерпретации BTA.

Если простого обдумывания не хватает, пользователь может переписать программу с целью обнаружения источника, препятствующего преобразованиям.

Чтобы упростить и ускорить написание кода, который хорошо специализируется, разработана и реализована история причин BT-разметки.

Проблема соотнесения места проявления проблемы с ее источником и устранение сложностей понимания, возникающих из-за откатов анализа, привела нас к решению в виде истории причин BT-разметки и ее визуализации.

История причин BT-разметки позволяет понять источник проблемы, почему тот или иной участок кода не специализируется и благодаря этому программист может внести улучшения времен связывания в свою программу.

Идея истории причин BT-разметки появилась при попытках применить JaSpe к реальным программам, разработанными другими авторами. Как и ожидалось, в таких программах содержится множество мест, которые не поддаются преобразованиям, а на поиск источников проблем уходит большее время, чем на их устранение. После реализации методов составления истории причин BT-разметки, их фильтрации и визуализации, время на поиск сократилось на порядок.

Для реализации истории причин потребовалось внести изменения в базовые понятия BTA, а именно в понятия BT-значение и BT-объект.

В оригинальных методах данные примитивных типов размечаются BT-значениями S или D, а данные ссылочных типов — BT-объектами. В классическом варианте [38] формальное определение BT-значения следующее:

BT-Value & { S,D } .

Расширим это определение для предоставления удобного способа составления истории причин. Вместо классического BT - V alue мы используем BT - V alue ^R .

BT-Value R = (BT-Value, Reason), где

Reason = (Kind R ,BT-Value R ,BT-Value R ,BT-Value R ,...) Здесь к классическому определению добавился тег Reason, который выражает причину, по которой то или иное BT-значение было создано и сохраняет BT-значения, на основе которых получено данное BT-значение.

Kind ^R — это целое число, идентификатор разновидности причины.

В реализации на его основе выбирается описание причины, подсказки и длина списка BT - V alue _i ^R . K ind ^R — элемент фиксированного множества. В описываемой реализации выделено 18 разновидностей причин.

История причин BT-разметки — сильный инструмент для поиска источника проблем, однако его невозможно эффективно применять без визуализации разметки программы. Проблема заключается в том, что без визуализации разметки непонятно, для какой конструкции необходимо рассматривать историю причин BT-разметки. Когда программист видит, что некое выражение получило D-разметку, он понимает, что это может быть отправной точкой для дальнейшего поиска источников. Если визуализации разметки нет, то придется пробовать наугад и такой перебор может занять продолжительное время.

10.    Пример анализа на основе истории причин BT-разметки

Рассмотрим основные идеи истории причин BT-разметки на уже знакомом примере с рисунка 1 . Для этого описания нам понадобится понятие BT-окружения.

BT-окружение — это структура данных, которая хранит текущую BT-разметку переменных. По сути это некоторая абстракция состояния памяти, в которой вместо обычных значений локальных переменных хранятся BT-значения. Можно считать, что BT-окружение — это хеш-таблица пар (имя переменной, BT -значение).

Определим множество возможных причин:

R def = (1 ,0 ) , — причина, означающая значение по умолчанию. Данная причина не зависит от других BT-значений.

R dep = (2 , BT-Value R , BT-Value R ,.. . ) — причина, которая сообщает, что данное BT-значение основывается на других BT-значениях и получено их обобщением.

R darg = (3 , 0 ) — причина, говорящая о том, что данное BT-значение построено для аргумента метода, которое пришло извне.

R ret = (4,BT-Value R ) — данная причина, указывает на то, что вызов метода получил разметку на основе BT-разметки его конструкции return.

Rvai = (5, BT-ValueR) — эта причина означает, что данное BT-значение получено из BT-окружения.

Может показаться, что для данного примера количество разновидностей причин избыточно. Можно было бы ограничится двумя R def и R _dep . Однако, в рассматриваемом подходе есть существенный плюс — для причин R _darg , R _ret и R _val можно выдать более детальные подсказки, что упрощает понимание получившейся разметки программы.

На рисунке 3 представлена размеченная программа с рисунка 1, в правую часть которого добавлены причины для соответствующих операторов.

• 1.    @Specialize

  {R darg

  R def R dep

  R def

  R def R dep

  R dep

  2x R var R ret R dep

  R def R var R ret R dep

  R def R var 2x R dep

  R var R dep

  
  

  2x R dep

  2x R var 2x R dep

  
  

• 2.    public static int example(int Argument)

• 3.     int a = 5;

• 4.     int result =0;

• 5.     boolean myTrue = true;

• 7.     if (!myTrue){

• 8.        result = sum (dArgument, a);

• 9.     } else {

• 10.        result = sum (a, 2);

• 11.}

• 12.    result = result * 2;

• 13.    return result ;

• 14.    }

• 15.

• 16.    pu blic st atic int sum(int a, int b) {

• 17.    return a + b;

• 28. }

Рисунок 3. Пример соотнесения причин

Мы не будем полностью разбирать программу, остановимся на ключевым моментах, остальные строятся по аналогии. Также мы не будем рассматривать базовую разметку, поскольку это сделано ранее в разделе 2 .

Анализ начинается со строки 2, в которой аргумент dArgument имеет D-разметку, так как он является аргументом точки входа. Поэтому для разметки выражения выбирается причина R _darg .

Рассмотрим строку 3: в ней определяется переменная a и выполняется присваивание константы. Константа 5 размечается парой (S,R _de f ). Причина R def выбрана потому, что S-разметка всегда выбирается для констант и является разметкой по умолчанию. Далее анализируется присваивание. Ему приписывается причина R dep , так как разметка присваивания целиком зависит от разметки выражения в правой его части.

В экземпляр этой причины помещается ссылка (S, R def ) на разметку правой части выражения.

Итоговая разметка присваивания целиком выглядит так:

(S, (2, (S, (1, 0 )))).

Это скобочное выражение изображает дерево BT-объектов. В общем случае оно оказывается ациклическим графом. Далее не будем приводить разметку целиком, сосредоточимся именно на причинах.

В строке 7 анализируется инструкция if . Так как разметка if зависит от разметки его условия, то причина — R d_ep .

В строке 8 анализируется присваивание и вызов метода. В вызов метода передаются два параметра — dArgument и a . Оба этих выражения приводят к обращению к BT-окружению и чтению из него соответствующих именам параметров BT-значений. Поэтому обоим выражениям-именам — dArgument и a— приписываются причина R _val (чтение из BT-окружения).

Далее анализ переходит непосредственно к самому вызову метода sum . Чтобы построить разметку этого выражения, мы должны узнать какова разметка результата этого метода. Поэтому BTA анализирует аргументы и тело этого метода.

Разметка аргументов определяется разметкой параметров. Поэтому оба аргумента получают причину R d_ep (строка 16). При этом BT-значения аргументов помещаются в BT-окружение.

Оператор return размечается как D из-за того, метод sum переходит return опирается на сумму a и b . в остаточную программу в форме метода sum_5_2 . Помипо этого, Итак, мы имеем два обращения к BT-окружению, для чтения a и b (причины R _val ), сумма a и b определяется значением подвыражений (причина R d_ep ) и return оприрается на сумму (тоже причина R d_ep ).

Разметка тела метода завершается и анализ наконец может определить разметку вызова — оно строится на основе разметки return (она D) и выбирается причина R ret .

Остальные конструкции программы получают причины по аналогии с уже разобранными случаями.

Покажем на этом примере как программист может использовать историю причин BT-разметки. Предположим, он хочет узнать, прочему в строке 12 переменная result (в правой части присваивания) получила D-разметку. Программист запрашивает историю причин BT-разметки, в которой сможет обнаружить следующую последовательность причин:

R var ← R dep ← R ret ← R dep ← R dep ← R var ← R dep ← R var ← R darg

История причин BT-разметки будет содержать ответвления от этой последовательности, но все ответвления будут с S-разметкой. Поэтому они не интересны с точки зрения обнаружения причины, по которой переменная result получила D-разметку.

Самой правой причиной в последовательности (1) является R _darg — это источник проблемы. В итоге программист обнаружит, что result имеет D-разметку в строке 12, косвенно зависящую от разметки аргумента dArgument в строке 1.

Обратим внимание на то, что место проявления проблемы (переменная result с D-разметкой) и источник проблемы (аргумент dArgument ) разнесены на достаточно большое расстояние для такой маленькой программы. В реальных программах время ручного поиска всего одной проблемы может занимать час и больше. Используя же историю причин, программист потратит две-три минуты.

В заключение приведем снимок экрана из JaSpe для выражения из примера выше (рисунок 4) .

• 5    public class BTValueExample {

  leasons of ВТ-Value(s)

  v® D | result

  • * ©D | if (ImyTrue) {| Generalization

  • >    © S | sum(a,2) | Contains expressions

  • *    © D | result=sum(dArgument,a) | Depends on expression

  *©D | sum(dArgument,a) | Contains expressions v© D | return a + b; | Contains expressions

  * © D | a + b | Contains expressions

  ^v © D | a + b | Contains expressions

  * © D | a + b | Contains expressions

  
  

• 7    ^Specialize

  |int dArgument|

  
  

• 9           int a = 5;

• 10          int result;

• 11          boolean myTrue = true;

13®          if (!myTrue) {

• 14              result I sum(dArgument, a);

15®          } else {

22® publ ic sta tic int sum (int a, int b) {

• 23         return | | b;

• 24     }

• 25    }

11.    Фильтрация истории причин BT-разметки

Рисунок 4. Снимок окна с историей причин BT-разметки для примера.

История причин BT-разметки построена для выражения из примера выше ( result в левой части присваивания строки 18 их кода). Сами причины отличаются, в реализации они иные, чем в примере. Каждая строка в истории причин BT-разметки — это конкретная причина. Первым в строке идет BT-значение. Далее после вертикальной черты — конструкция Java, к которой относится причина, а затем — разновидность причины.

Первая строка истори причин BT-разметки соответствует выражению result. Далее идет дерево причин, где отступ от левого края означает вложенность.

На снимнке мы видим, что result «наследует» разметку по цепочки из D-причин, которая ведет к аргументу метода dArgument — это ситуация аналогична разобранному примеру.

В предыдущих двух разделах изложены базовые понятия и идеи истории причин BT-разметки, а также проиллюстрировали методы работы с причинами на примере. В этом разделе мы разберем как эффективно фильтровать причины, существенно сокращая время поиска источника проблемы.

Обычно при построении истории причин BT-разметки получается большой ациклический граф. Для того, чтобы не потеряться в массиве информации нужно фильтровать такой граф для выявления ключевой информации.

Причины разделяются на две категории: источники и промежуточные причины . Источники — это такие причины, которые связаны с созданием новых BT-значений (в противоположность промежуточным причинам). Обычно источники не основываются ни на каких других причинах, то есть являются листьями в графе истории причин BT-разметки. Из примера в предыдущей главе можно выделить две разновидности причин, которые будут являться источниками — R _def и R _darg .

Другая категория причин — промежуточные причины. Промежуточные причины основаны на наследовании BT-значений от других конструкций. В примере это R dep , R ret и R val , так как маркируемые этими причинами BT-значения полностью зависят от других (дочерних) BT-значений. Эта категория причин как бы передает BT-значения из одного места в другое.

Отметим, что важны источники D-значений, поскольку они позволяют найти начальные точки, которые ограничивают специализацию.

Чтобы решить проблему массивности истории причин BT-разметки, реализована система фильтрации истории причин. Теперь можно визуализировать только источники, оставляя все остальные причины в стороне. Для графа из десятков тысяч причин получались только 6-7 единиц причин-источников.

Нужно заметить, что промежуточные причины не так уж бесполезны. Во-первых, они могут быть важны начинающим пользователям специали-затора, чтобы понять, по каким правилам D-значение передалось от источника до места, в котором пользователь ожидал преобразование. Во-вторых, трасса от источника до места проявления проблемы может быть полезна и опытным программистам, чтобы рассеять недопонимание происходящих в BTA процессов. Это особенно актуально для больших и сложных программ.

12.    Типовой сценарий использования истории причин BT-разметки

Опишем основной сценарий специализации с анализом истории причин BT-разметки:

• (1 )    Пользователь применяет JaSpe к программе.

• ( 2 )    В результате пользователь получает неэффективную остаточную программу.

• (3 )    Пользователь находит в остаточной программе, места, которые не специализируются вопреки его ожиданиям.

• (4 )    Пользователь изучает BT-разметку исходной программы в тех местах, где он ожидал преобразования.

• (5 )    Программист ожидал S, а получил D в ключевом на его взгляд месте и хочет понять почему.

• (6 )    На подсвеченных D результатах BTA пользователь смотрит трассу причин.

• (7 )    Пользователь запрашивает у системы фильтрацию промежуточных причин.

• (8 )    Пользователь находит источник(и) проблем — те выражения, которые послужили источниками D-значений.

• (9 )    Пользователь производит рефакторинг кода, чтобы убрать найденные D-источники (это называется улучшением времен связывания).

• (10 )    Эта процедура выполняется итеративно начиная с шага 1 до тех пор, пока пользователь не будет удовлетворен результатом.

Суть этого сценария заключается в том, что пользователь делает некоторые предположения, как должна быть специализирована его программа, и применяет специализатор исходя из этих соображений. Затем пользователь сверяет свои ожидания с реальным результатом и с помощью интерактивных средств понимает, где ожидания не оправдываются.

Без интерактивных средств понимание причины расхождения ожиданий и реальности требует намного более серьезных усилий и квалификации в области частичных вычислений.

Заключение

Все известные автору исследования в области частичных вычислений концентрируются на использовании специализатора в режиме черного ящика. В итоге они либо не получают широкого практического применения, либо используют самые простые преобразования.

Для масштабирования по-настоящему сильных методов частичных вычислений требуется включение человека в процесс специализации. Переход от режима черного ящика к интерактивной специализации сравним с переходом от связки компилятор и простой текстовый редактор к современным IDE, содержащим множество интерактивных средств помощи программисту.

В настоящей статье рассмотрены понятия и методы интерактивной специализации на основе частичных вычислений, которые позволяют существенно снизить нагрузку на программиста-пользователя. После реализации этих методов на практике обнаружилось, что в некоторых случаях, время, которое тратит человек на устранение проблем с преобразованиями, сокращается на порядок.

Для реализации интерактивных средств разработаны следующие методы и принципы:

• ^•    Методы выполнения BTA на основе AST программы.

• ^•    Принципы визуализации разметки программы.

• ^•    Методы построения и фильтрации истории причин BT-разметки и понятия с этим связанные.

Методы построения и работы с историей причин BT-разметки изучаются впервые. Эти методы не зависят от специфики BTA и мы рассчитываем, что история причин BT-разметки может быть применена в других методах анализа программ, основанных на абстрактной интерпретации, в составе интерактивных средств.

Также пришлось модифицировать такие базовые понятия частичный вычислений для программ на объектно-ориентированных языках, как BT-значение и BT-объект. Причинами изменения базовых понятий является то, что в них было необходимо включить понятие причин разметки, а также собрать множество вспомогательных понятий в более удобную и целостную форму.

Все разработанные понятия и методы опробованы в специализаторе JaSpe — частичном вычислителе для программ на языке Java. Этот специализатор погружен в Eclipse IDE.

Планируется применить JaSpe к интерпретатору языка SL, который разработан команией Oracle для своего специализатора в составе GraalVM. Такое применение позволит сравнить описанный метод с ранее существующими.