Интерактивный метод формирования вариантов решений отдельного производителя
Автор: Трояновский В. М.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Информатика и управление
Статья в выпуске: 2 (58) т.15, 2023 года.
Бесплатный доступ
Излагается метод формирования вариантов организационных решений с использованием такого инструмента, как динамическое программирование, и неформального анализа, проводимого лицом, принимающим решение, на основе полученных результатов расчетов. Обосновывается возможность использовать такой подход для объединения методик формальных расчетов с опытом специалистов-управленцев.
Динамическое программирование, разработка вариантов решений, формальные и неформальные методы
Короткий адрес: https://sciup.org/142237749
IDR: 142237749 | УДК: 519.86
Текст научной статьи Интерактивный метод формирования вариантов решений отдельного производителя
Исследованию работы отдельного производителя посвящены многочисленные издания, назовем [1, 2]. В данной публикации рассматривается возможность сочетать формальные методы анализа, задач, возникающих в процессе функционирования отдельного производителя, и неформальное, качественное оценивание ситуации, основанное на. опыте лица, принимающего решение (ЛПР). При формировании вариантов решений, безусловно, необходимо учитывать все существенные варианты. Одновременно желательно избежать ситуации, когда, варианты начинают плодиться, грозя утопить ЛПР в неподъемной работе по их осмыслению. Кроме того, в практической деятельности желательно иметь не только эффективный, но и достаточно простой метод формирования вариантов для дальнейшего их анализа. Опишем один из таких человеко-машинных методов формирования вариантов решения, используя для этого иллюстративный пример.
Пусть есть отдельный производитель, продукт которого приобретают три покупателя, и есть три поставщика, ресурса, необходимого данному производителю. Планирование его работы осложняется тем, что затраты на. ресурс и реализация произведенного продукта, разнесены во времени. В таком случае производителю становится целесообразным заботиться о минимизации себестоимости производимого продукта, и о максимизации дохода, от его реализации. Возможности минимизировать себестоимость у данного производителя довольно ограниченные, т.к. цену ему объявляет владелец ресурса. Максимизация дохода, наоборот, зависит от указанного производителя, но вполне определенным образом.
«Московский физико-технический институт (национальный исследовательский университет)», 2023
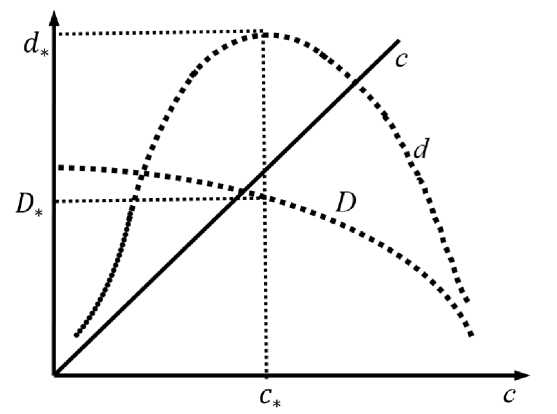
Рис. 1. Зависимость дохода от спроса и цены
Ситуация показана на рис. 1. Представление зависимости спроса D (c) и до хода d(c) от цены c в виде точечных кривых означает, что реализация произведенного продукта происходит какими-то дискретными порциями. На этом рисунке доход d = cD имеет максимум (все отвечающие ему значения помечены нижними звездочками) и значения дохода, стремящиеся к нулю, по краям.
При наличии нескольких поставщиков ресурса (каждый из которых продает свой продукт по своей цене) и нескольких потребителей (каждый из которых имеет свою кривую зависимости D(c)), прежде всего, возникают вопросы о том, у кого сколько покупать и кому сколько продавать. Получить необходимую информацию, которая позволила бы провести дальнейший анализ вариантов решений, можно с помощью динамического программирования, которое излагается во многих книгах, см., например, [3].
Пусть есть следующие исходные данные для примера, который будет иллюстрировать суть предлагаемого метода. Для каждого из трех потребителей продукта данного производителя известен доход {Д (N )}, к = 1, 2, 3, который он приносит производителю, приобретая товар в количестве N единиц, N = 1,..., 15. Для каждого из трех поставщиков известны затраты на ресурс {д ^ (N )} для N единиц производимого в дальнейшем продукта. Эти исходные данные представлены в табл. 1 и 2.
Т а б л и ц а 1
Доход от продажи разным потребителям в зависимости от объема продаж
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
N / /X |
|
|
к |
40 |
60 |
90 |
110 |
80 |
50 |
40 |
20 |
18 |
16 |
14 |
12 |
10 |
8 |
5 |
100 |
|
30 |
50 |
80 |
90 |
100 |
70 |
50 |
20 |
17 |
15 |
12 |
10 |
8 |
5 |
3 |
100 |
|
|
50 |
60 |
80 |
70 |
50 |
30 |
20 |
10 |
9 |
8 |
6 |
4 |
3 |
2 |
1 |
100 |
Т а б л и ц а 2
Расход при закупке у разных производителей в зависимости от объема производства
|
X |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
И |
12 |
13 |
14 |
15 |
/ X |
|
81 |
55 |
100 |
140 |
175 |
203 |
230 |
245 |
257 |
284 |
276 |
284 |
291 |
297 |
302 |
306 |
10 |
|
82 |
30 |
78 |
115 |
145 |
173 |
200 |
225 |
245 |
260 |
273 |
284 |
294 |
302 |
309 |
315 |
10 |
|
8з |
10 |
60 |
105 |
145 |
180 |
210 |
238 |
260 |
282 |
302 |
317 |
327 |
335 |
341 |
345 |
10 |
В обеих таблицах в крайних правых столбцах указаны множители, которые оказались необходимыми, чтобы разместить таблицы в поле текста страницы без дробных частей.
Покажем на примере для N = 14-4 определение максимального дохода производителя и соответствующего распределения объемов продаж разным потребителям.
Как это делают в динамическом программировании, сначала для всех значений п1 = N 4- 0 и значений П2 = 0 4- N находим для очередного значения N величину Ғ12 = max{/1 (п1) + /2(N — п1 )} для всех комбинаций п1 и п2, сумма которых не превосходит N. Указанный расчет и определение искомой комбинации п1 — Н2 показаны в табл. 3.
Т а б л и ц а 3
Расчет максимальных значений дохода для двух потребителей
|
N |
«Ь И2 |
//+/2 |
nf, п2 |
Ғ 12 |
|
1 |
1;0 |
40 + 0 = 40 |
1-0 |
40 |
|
0; 1 |
0 + 30 = 30 |
|||
|
2 |
2; 0 |
60 + 0 = 60 |
1-1 |
70 |
|
1; 1 |
40 + 30 = 70 |
|||
|
0; 2 |
0 + 50 = 50 |
|||
|
3 |
3; 0 |
90 + 0 = 90 |
3-0 2-1 1-2 |
90 |
|
2; 1 |
60 + 30 = 90 |
|||
|
1;2 |
40 + 50 = 90 |
|||
|
0; 3 |
0 + 80 = 80 |
|||
|
4 |
4; 0 |
110 + 0= 110 |
3-1 1-3 |
120 |
|
3; 1 |
90 + 30= 120 |
|||
|
2;2 |
60 + 50= 110 |
|||
|
1; з |
40 + 80=120 |
|||
|
0; 4 |
0 + 90 = 90 |
Затем таким же образом рассчитываются значения величины Ғ123 для всех трех покупателей. Ход расчетов и результаты показаны в табл. 4.
Т а б л и ц а 4
Расчет максимальных значений дохода для трех потребителей
|
N |
«у + 'Щ Из |
Ғ12 |
Ь |
Ғ12 + /з |
П1-И2-П3 |
Ғ123 |
|
1 |
1;0 |
40 |
0 |
40 + 0 = 40 |
0-0-1 |
50 |
|
0; 1 |
0 |
50 |
0 + 50 = 50 |
|||
|
2 |
2; 0 |
70 |
0 |
70 + 0 = 70 |
1-0-1 |
90 |
|
1; 1 |
40 |
50 |
40 + 50 = 90 |
|||
|
0; 2 |
0 |
60 |
0 + 60 = 60 |
|||
|
3 |
3; 0 |
90 |
0 |
90 + 0 = 90 |
1-1-1 |
120 |
|
2; 1 |
70 |
50 |
70 + 50= 120 |
|||
|
1;2 |
40 |
60 |
40 + 60= 100 |
|||
|
0; 3 |
0 |
80 |
0 + 80 = 80 |
|||
|
4 |
4; 0 |
120 |
0 |
120 + 0= 120 |
3-0-1 2-1-1 1-2-1 |
140 |
|
3; 1 |
90 |
50 |
90 + 50 = 140 |
|||
|
2; 2 |
70 |
60 |
70 + 60= 130 |
|||
|
1; з |
40 |
80 |
40 + 80 = 120 |
|||
|
0; 4 |
0 |
70 |
0 + 70 = 70 |
Аналогично находятся минимальные затраты. В табл. 5, 6 показаны все результаты для N = 15.
Две последние табл. 5 и 6 являются уже рабочими для ЛПР, т.к. в них содержит- ся информация о предпочтительных распределениях покупателей и поставщиков. Кроме того, эти таблицы являются базой для построения следующих таблиц, необходимых для разработки вариантов решений. Очередная таблица, табл. 7, имеет четыре входа. Две левые колонки и две верхние строки являются входами для определения величин упущенной выгоды (см. верхний треугольник над диагональю, идущей от левого верхнего угла в правый нижний угол). Правый столбец и нижняя строка - входы для определения величины омертвленного капитала. Так как табл. 7 целесообразно иметь целиком, ее пришлось расположить в альбомном варианте, как и следующую табл. 8 следом за табл. 7.
Т а б л и ц а 5
Сводная таблица всех результатов расчета (начало)
|
N |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
Прибыль г |
4900 |
8600 |
11120 |
12750 |
15450 |
17170 |
19900 |
21650 |
22450 |
|
|
Себестоимость m |
100 |
200 |
293 |
300 |
310 |
305 |
300 |
294 |
283 |
|
|
Ғпз |
5000 |
9000 |
12000 |
14000 |
17000 |
19000 |
22000 |
24000 |
25000 |
|
|
F |
nrn2-n3 |
0-0-1 |
1-0-1 |
1-1-1 |
3-0-1 1-2-1 2-1-1 |
1-3-1 3-1-1 |
4-1-1 3-2-1 2-3-1 |
3-3-1 |
4-3-1 |
4-4-1 4-3-2 3-3-3 |
|
Q |
С123 |
100 |
400 |
880 |
1250 |
1550 |
1830 |
2100 |
2350 |
2550 |
|
ХГХ2-Х3 |
0-0-1 |
0-1-1 |
0-2-1 |
0-3-1 |
0-4-1 |
0-5-1 |
0-6-1 |
0-7-1 |
0-8-1 |
|
Т а б л и ц а 6
Сводная таблица всех результатов расчета (окончание)
|
N |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
Прибыль г |
24300 |
25170 |
26090 |
25030 |
22980 |
20940 |
|
|
Себестоимость m |
270 |
257 |
242 |
228 |
216 |
204 |
|
|
F |
Ғүв |
27000 |
28000 |
29000 |
28000 |
26000 |
24000 |
|
П1-П2-П3 |
4-3-3 |
4-4-3 |
4-5-3 |
4-5-4 |
4-5-5 |
4-5-6 |
|
|
G |
С123 |
2700 |
2830 |
2910 |
2970 |
3020 |
3060 |
|
xl-x2-x3 |
0-9-1 |
0-10-1 |
12-0-0 |
13-0-0 |
14-0-0 |
15-0-0 |
|
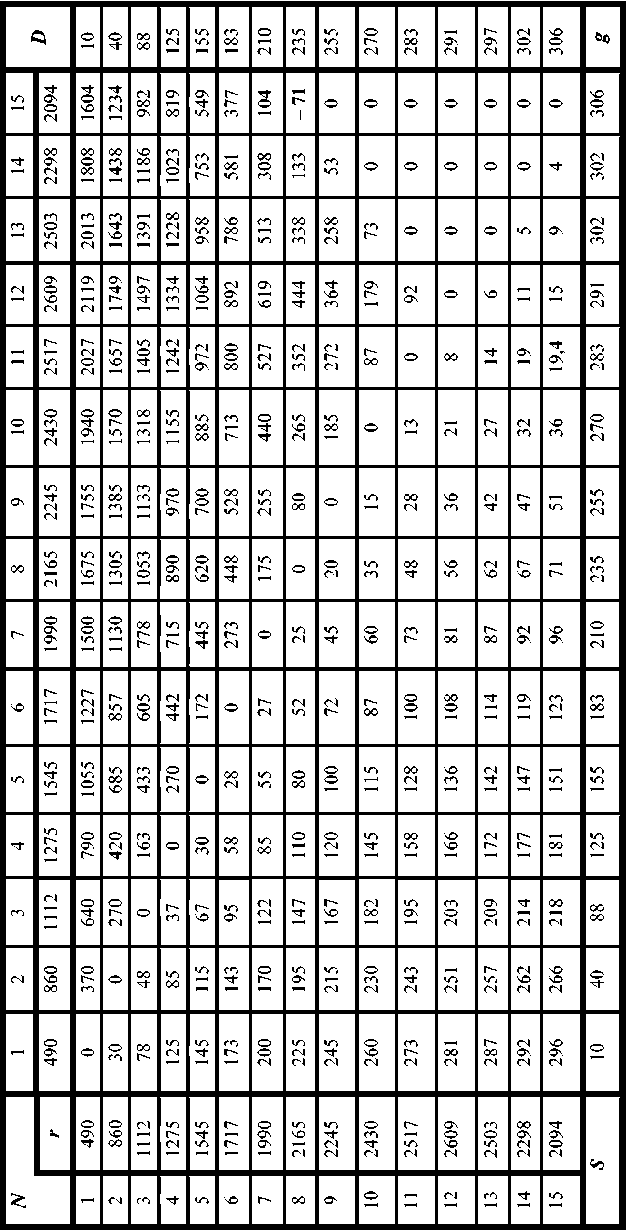
Упущенная выгода считается естественным образом. При N2 ^ N1 из прибыли r(N2 ) для двух верхних строк вычитается прибыль r(Ni) двух левых столбцов. В строке N1 = 8 и столбце N2 = 15 стоит отрицательная величина -71 = 2094 — 2165. Т.к. упущенная выгода не может быть отрицательной, в указанной клеточке табл. 7 должен стоять ноль, как он стоит в других аналогичных случаях.
Под омертвлением капитала понимается простейшая (довольно примитивная) ситуация выпуска продукции в объеме N 1 (левый столбец), превысившим спрос У 2 (верхняя строка) на данном шаге функционирования производителя. Более сложному анализу, скажем, выпуску продукции с учетом создания запасов или с учетом роста стоимости ресурсов в результате инфляции, посвящены многие работы (в частности, работа [4] автора). Такие исследования пока не рассматриваются, т.к. охватывают круг вопросов и проблем, значительно отличающихся от формирования «вручную» вариантов решений.
Результаты расчета содержатся в нижнем треугольнике, под упоминавшейся диагональю. Расчет ведется следующим образом. При N2 ^ N1 из величины произведенных затрат на производство g(Ni ) правого столбца вычитается величина затрат g(N2 ) нижней строки на производство продукции в объеме N2, которое удалось реализовать. Скажем, если произвести Ni = 12 единиц продукцни с затратами g(Ni ) = 2910, а продать только N2 = 10, что потребовало бы затрат лишь g(N2) = 2700, то омертвленными оказываются затраты в 210 единиц.
Т а б л и ц a 7
Полные финансовые сведения о вариантах производства продукта (все величины, кроме значений N, надо умножить на 10)
Т а б л и ц a 8
Значимые финансовые сведения о вариантах производства продукта (все величины, кроме значений N, надо умножить на 10)
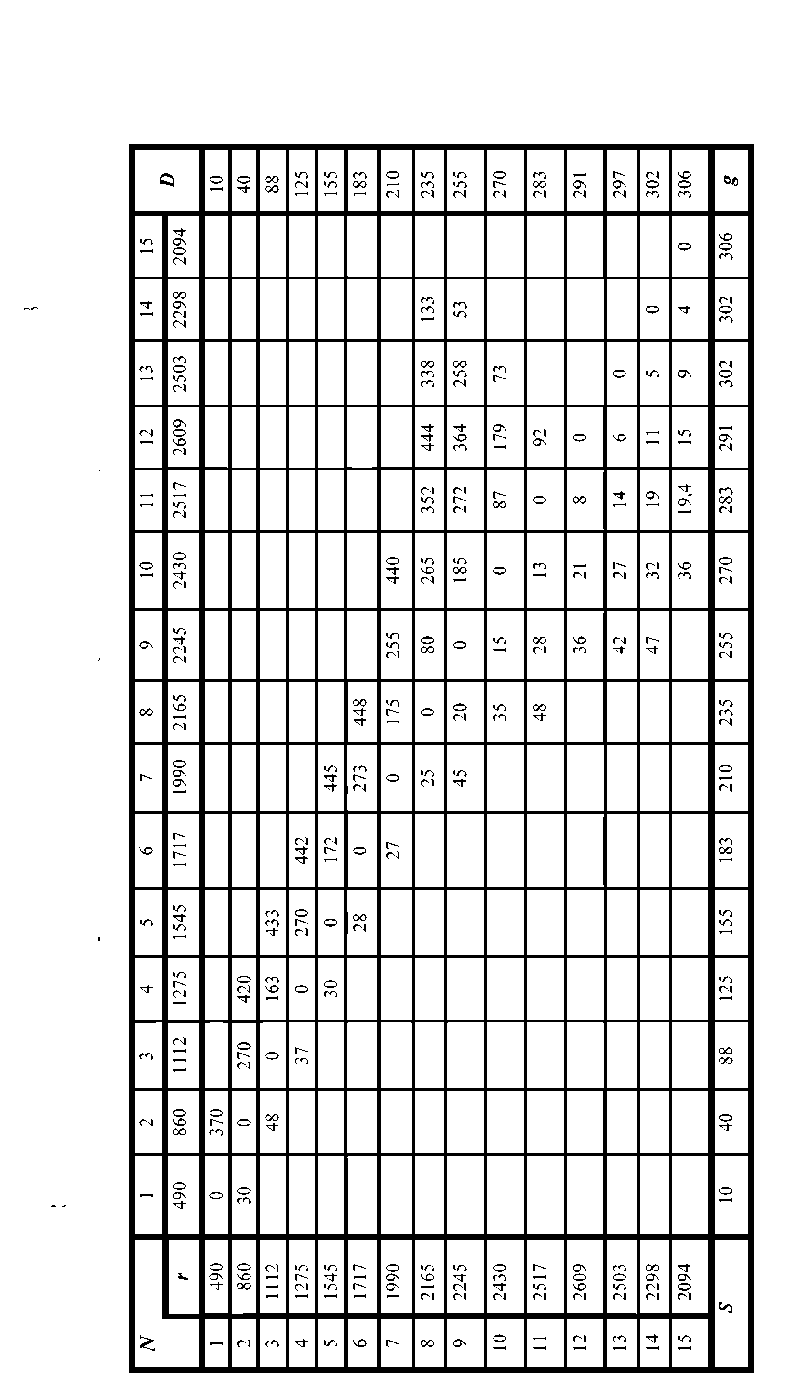
Таблица 7 может быть полезной для анализа ситуации в том случае, когда ЛИР принимает активное и во многом неформальное участие в формировании вариантов решений. Основой такого участия могут быть накопленный опыт, понимание перспективы развития, дополнительные сведения (расчеты, экспертные оценки и т.д.). Это участие может заключаться, в частности, в том, что сразу определяются некоторые граничные условия для вариантов.
Естественно предположить, что в условиях неопределенности будущего спроса Л ПР, прежде всего, хотел бы выделить необходимый для принятия решения существенный объем сведений. Для этого он может задать, скажем, такие границы: упущенная выгода не более 5000, омертвление капитала не более 500. В результате использования этих ограничений из табл. 7 получается табл. 8, упоминавшаяся выше (в ней еще удалены «лишние» нули, оставлены только нули диагонали, которая разделяет принципиально различающиеся верхний и нижний треугольники). Комбинации значений N, в клетках которых отсутствуют данные, не рассматриваются.
Далее ЛПР может в силу ряда соображений прийти к выводу, что объем выпуска N должен быть не менее определенной величины (скажем, N ^ 8). Тогда последнюю таблицу можно преобразовать в табл. 9.
Т а б л и ц а 9
Значимые для ЛПР сведения (х10, кроме N)
|
N |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
D |
|
|
Г |
2165 |
2245 |
2430 |
2517 |
2609 |
2503 |
2298 |
2094 |
||
|
8 |
2165 |
0 |
80 |
265 |
352 |
444 |
338 |
133 |
235 |
|
|
9 |
2245 |
20 |
0 |
185 |
272 |
364 |
258 |
53 |
255 |
|
|
10 |
2430 |
35 |
15 |
0 |
87 |
179 |
73 |
270 |
||
|
11 |
2517 |
48 |
28 |
13 |
0 |
92 |
283 |
|||
|
12 |
2609 |
36 |
21 |
8 |
0 |
291 |
||||
|
13 |
2503 |
42 |
27 |
14 |
6 |
0 |
297 |
|||
|
14 |
2298 |
47 |
32 |
19 |
11 |
5 |
0 |
302 |
||
|
15 |
2094 |
36 |
19,4 |
15 |
9 |
4 |
0 |
306 |
||
|
S |
235 |
255 |
270 |
283 |
291 |
297 |
302 |
306 |
8 |
|
Конечно, могут быть и другие, не менее важные для ЛПР ограничения, скажем следующие. Если доход должен быть не менее 21500, то должно быть: 7 ^ N ^ 15. Если прибыль должна быть не менее 22000, то должно быть 9 ^ N ^ 14. Если себестоимость должна быть не более 275, то 10 ^ N ^ 15. В итоге получается, что для ЛПР интерес представляют лишь варианты производства 10 ^ N ^ 14, показанные в табл. 10.
Т а б л и ц а 10
Итоговые сведения
|
N |
10 |
И |
12 |
13 |
14 |
|
|
Г |
24300 |
25170 |
26090 |
25030 |
22980 |
|
|
10 |
24300 |
0 |
870 |
1790 |
730 |
|
|
11 |
25170 |
130 |
0 |
920 |
||
|
12 |
26090 |
210 |
80 |
0 |
||
|
13 |
25030 |
270 |
140 |
60 |
0 |
|
|
14 |
22980 |
320 |
190 |
110 |
50 |
0 |
|
Доход Ғ,2з |
27000 |
28000 |
29000 |
28000 |
26000 |
|
|
пгп2-п3 |
4-3-3 |
4-4-3 |
4-5-3 |
4-5-4 |
4-5-5 |
|
|
Расход С|23 |
2700 |
2830 |
2910 |
2970 |
3020 |
|
|
хгх2-х3 |
0-9-1 |
0-10-1 |
12-0-0 |
13-0-0 |
14-0-0 |
|
|
Себестоимость т |
270 |
257 |
242 |
228 |
216 |
|
Как видно из содержания табл. 10, задача выбора предпочтительного варианта реше- ния остается многокритериальной. Но в результате проведенного исследования объем исходных сведений резко сократился. Это допускает уже достаточно эффективный анализ «вручную».
Первым претендентом на использование в качестве искомого решения является вариант с максимальной прибылью. Но ситуация непростая и требует дополнительного анализа, для чего приведен рис. 2. На этом рисунке не соблюдены масштабы указанных величин, поэтому имеется именно рисунок, а не диаграмма.
|
5 Я оЗ 5 о § >> |
1790(12) |
||||
|
870 (11) 730 (13) |
920 (12) |
||||
|
N |
10 |
И |
12 |
13 |
14 |
|
Ж 3 § s о. § о |
130 (10) |
80(11) |
60(12) |
50(13) |
|
|
210(10) |
140(11) 270 (10) |
110(12) 190(11) |
|||
|
320 (10) |
|||||
Рис. 2. Сравнение вариантов решения
Максимум прибыли производитель получит, реализовав 12 единиц своей продукции (см. табл. 6). Доход и прибыль при большем объеме продаж производитель не получит по причине, описанной в комментариях к рис. 1. В силу этого, начиная с N = 12, упущенная выгода будет нулевой для значений N = 12 4-14. Получается, что среди вариантов с N = 12 4-14 вариант при N = 12 является бесспорным лидером. Этому варианту, в отсутствие достоверной информации, проигрывает и вариант с объемом выпуска N = 11, т.к. при несколько меньшем омертвлении капитала этот вариант может привести к существенной упущенной выгоде. Это же можно сказать и о варианте N = 10. Исключать два последних указанных варианта, конечно, нельзя, но их использование будет связано, скорее всего, либо с вынужденной чрезмерной осторожностью ЛПР (нежеланием идти на риск омертвить капитал), либо с его точным знанием будущей ситуации.
Анализ, для которого предназначен рис. 2, не исключает привлечения уже разработанных методов решения многокритериальных задач. Возможно, при этом будут привлечены дополнительная исходная информация или дополнительные критерии оценивания. Но это все равно не будет попыткой заменить человека, ЛПР, а тем более исключить его из процесса разработки и принятия решения с помощью каких-то формальных процедур. Такое положение вещей объясняется следующим обстоятельством.
Как отмечено в [5], предприниматель стремится минимизировать вероятность разорения. В этой работе показано, что в простейшем случае, когда масштаб предпринимательской деятельности невелик, следование этому принципу выливается в стремление максимизировать прибыль. При значительных масштабах деятельности поведение предпринимателя более сложное. ЛПР, основываясь на прошлом опыте, состоянии экономики, прогнозах ее развития, целях разного горизонта планирования, может выбрать не самый хороший, на первый взгляд, вариант. В силу этого, вполне возможно, ЛПР станет выбирать между вариантами 12 (ради максимизации текущей прибыли) или 13 (скажем, ради расширения рынка сбыта) и вероятно, уже «вручную» неформальным образом.
Список литературы Интерактивный метод формирования вариантов решений отдельного производителя
- Поспелов И.Г. Однопродуктовое описание воспроизводства экономики. Москва: МФТИ, 2015. 78 с.
- Ширяев В.И., Баев И.А., Ширяев У.В. Экономико-математическое моделирование управления фирмой. Москва: URSS, 2007. 224 с.
- Кремер Н.Ш., Путко Б.А., Тришин И.М. Исследование операций в экономике. Москва: URSS, 2023. 414 с.
- Трояновский В.М. Функционирование производителя в условиях инфляции. Москва: Издателвство РДЛ, 2013. 53 с.
- Петров А.А., Поспелов И.Г. Шананин А.А. Опви математического моделирования экономики. Москва: Энергоатомиздат, 1996. 544 с.


