Интеративный расчет ДОЭ, фокусирующих в объем и на поверхность вращения

Известны итеративные методы для расчета фазовых дифракционных оптических элементов (ДОЕ), которые фокусируют лазерное излучение в пространственные плоские фигуры (изображения) [1,2]. Для расчета ДОЕ в обпемные фигуры, используют разбиение на N плоскостей и сведение задачи к расчету ДОЕ, формирующего плоские изображения. В [3,4] предложены различные подходы. В [3] независимо рассчитываются комплексные амплитуды Г^х,У), преобразование Френеля которых связано с заданным распределением интенсивности 4(?,п) на плоскостях z=z_n (см. рис.1) уравнением

7„(5,П) = |3„{/„(х,>-)}|2

где З_п{ } - преобразование Френеля на плоскость z=z_n.

Рис.1 Оптическая схема для фокусировки с помощью ДОЕ в 3—х мерную область.

Результирующая функция пропускания ДОЕ равна арифметическому среднему:

1 N /(*,>') = Т7^/-.(ДС’>')                               <2)

N л=0

Далее для замены амплитудно-фазовой функции Кл,У) на только фазовую функцию используют обычные процедуры кодирования в цифровой голографии [5].

В работе [4] функции Г^х,У) рассчитываются взаимосвязанно, а не независимо, что позволяет в ходе итеративного процесса получить только фазовую функцию без дополнительных (малоэффективных) процедур кодирования.

В [6] рассматривалась в приближении геометрической оптики задача расчета ДОЕ, фокусирующего на поверхность вращения с осью z.

В данной работе используя иной подход, рассматриваются итеративные методы расчета фазовых ДОЕ, фокусирующих лазерное излучение в объем и на поверхность тел вращения.

1. Общее рассмотрение.

Оптическая схема на рис.1 показывает, что ДОЕ, который рассматривается как тонкий фазовый транспарант, освещается плоской волной света с длиной волны Х=2л/£, к — волновое число, и формирует на расстояниях вдоль оптической оси z , n = \,N, заданные распределения интенсивности Л/^-г]).

Рассмотрение проводится в рамках скалярной волновой теории дифракции Кирхгофа в приближении Френеля.

В [4] описан алгоритм расчета функции пропускания ДОЕ с помощью итеративной процедуры минимизирующей функционал

^M = "Z J Jfl^K. n,z„)| - ЛК. п)]²<К d п

И = 1

где

^Л^^Л), n=VN

, х к ее

F(^,ri,z„) = 3n{e'r(xJ,)} = — ffexp /Дх,^) +

^-|(х-У2+Су-п)2| dxdy

гце Дх,у) искомая фаза ДОЕ, который формирует световое поле с комплексной амплитудой F^t^z), модуль которой совпадает на заданных расстояниях z_n с требуемой амплитудой A^v^z^, П — форма апертуры ДОЕ.

Итеративный алгоритм, минимизирующий средне квадратичное отклонение (3), имеет вид:

ТДх,у) = arg £ и^Чх.у)

_ л=1

и^Ч^.У) = Л^ЛК.фехррй^К.п)]}

5„.,K,n) = ari

^„{expp^iCx,/)]^

где р — номер итерации, Qn,^^ ^— фаза светового поля на плоскости, отстоящей от ДОЕ на расстоянии z_n и рассчитанная на р- ой итерации.

Ниже рассматриваются различные варианты итеративного алгоритма минимизирующего функционал средне квадратичного отклонения вида

MJ

е'^-^С^/х^) dxd^

где С_п — комплекснозначные весовые множители.

Функционал (3), записанный в плоскостях, отстоящих от ДОЕ на расстояниях z_n , можно с помощью равенства Парсеваля записать в плоскости ДОЕ:

Л=1 Q

Функции Щх,У) в уравнениях (8) и (9) являются результатом вычисления обратного преобразования Френеля:

^(^^’{Л^П)}

^il^ АС^^^Ррбл^’1!)]

Если переписать функционал (9) в обобщенной форме с весовыми коэффициентами

^^Jle'74''’-^^^.^

”=1 о

то нетрудно получить уравнение, связывающее значения обоих функционалов

М' = М + f f С„< JJ U^x.yW^x.y) d x d у - (N - 1) ■ ^        (13)

где

»(, = jj[eir,,'y,|!dxd>’ Q

• — полная световая энергия в плоскости ДОЕ.

Из уравнения (13) видно, что функционалы Mi и М равны с точностью до несущественной постоянной (N~ 1)-Wo при ортогональности функций U_nVx,yY то есть при выполнении условия:

ff ^(^.^^(x.^dxd^ = JjFJ^^/^’^.^d^dn = ^05™ О                                        -ОО

где бтд — символ Кронекера. Функционал общего вида (8) имеет произвол в выборе функций Qn(^,n).

Условию ортогональности (14) можно удовлетворить, задавая амплитудные функции на плоскостях фокусировки в зоне дифракции Френеля А_л(^,г|) с пространственно разделенными носителями, то есть области G_m в которых амплитуды А_л(^,г|) отличны от нуля, не пересекаются между собой:

G„nG„ = 0, m,n = \N                      (16)

Такое условие реализуется при расчете разовых ДОЕ, формирующих моды Гаусса-Эрмита или Гаусса-Лагерра в различных порядках дифракции [7,8].

Условию (15) можно также удовлетворить , разделив апертуру ДОЕ О на N непересекаюшихся субапертур О_л,, ^в каждой из которых задается функция U_n

^_п^_т=^^ m,n=\N                  (17)

Разбиение апертуры ДОЕ, например, на кольцевые субапертуры применяется при расчетах аксиконов и формирователей бесселевых мод [9], а также при использовании метода конечных элементов для расчета ДОЕ [101.

Минимизация функционала (8) эквивалентна поиску коэффициентов С_п. обеспечивающих выполнение следующего равенства

Л=1

где функции Щх,у) определяются уравнениями (10), (11) и в общем случае неортогональные. Уравнение (18) можно рассматривать как двумерную проекцию трехмерной задачи:

_e.T(x,y.z) ₌ y^C_nU_n(x,y)\v_n(z) (19)

где функции Уп(г) ортогональны:

jv,(z)<(z)dz = 5m„                        (20)

О

Если, например, функции (20) выбрать в виде

\|/„(z) = ехр[/2ллг]                                 (21)

то коэффициенты суммы (19) вычисляются с помощью соотношений:

с, = ^'Л ^LA^x,y)U‘„(x,y')dxdy

Q

L„(x,y) ⁼ f ^ехРр T(x,y,z) - /27tnz]d z о

С учетом уравнений (18)—(23) получим итеративный алгоритм минимизации функционала (8):

T/x^z^arg

N

UAx^e'1”"

-"=1

D„., = ^аг§ Л kp<^x>y'>^U*Ax,y')dxdy

к,,<х,У) = J exppT^Cx^.z) -z27Uiz]dz о где 5^0 — произвольные положительные числа, р — номер итерации. Искомая фазовая функция ДОЕ получается как проекция на ось z=0:

Т_р(х,у)=ТДх,у,2 = 0)                         (27)

Сходимость в среднем алгоритма (24)—(26) показана в Приложении.

• 2. Фокусировка в радиально-симметричную область.

На рис.2 показана оптическая схема для расчета ДОЕ, фокусирующего излучение на РЯД плоскостей, являющихся круглыми сечениями тела вращения. При этом амплитуда ^zX^n) на каждой из плоскостей зависит в полярных координатах ^=p cosG, T]=p-sin6 только от радиальной переменной р: Лд(р).

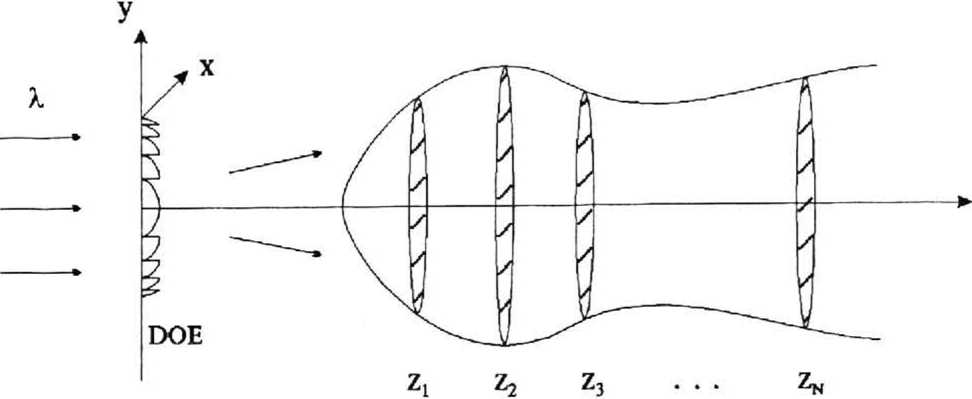
Рис.2 Оптическая схема для фокусировки с помощью ДОЕ в тело вращения.

Тогда вместо уравнений (19) и (22) в данном случае можно записать:

е'^т<^>₌ ^_С„У„(г)е'"^ф Л=1

Л 2л

С„ = (2n^)'J/е^’^е^гагаф             (29)

о о

(Ш = з;’{л„(р)е'е"<‘,)}

где (г,<р) — полярные координаты в плоскости ДОЕ, Jg(x) — функция Бесселя нулевого порядка. Уравнение (30) является обратным преобразованием Френеля в полярных координатах.

Если интенсивность внутри сечений тела вращения постоянная, то амплитуду Ап(р) можно выбрать в виде

4(р)=circ(—]                           (31)

VPoV где

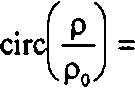
L Р^Ро

0, р>Ро

и 1_п — постоянные значения интенсивности в круге на каждой плоскости.

Произвольные фазы Q^p) в уравнении (30) можно выбрать квадратичными:

й(р)=^

2z.

а постоянные интенсивности 1_п выбираются из условия сохранения энергии

лрХ = %, »=1Л

Подставив выражения (31)—(33) в уравнение (30), получим конкретный вид функций разложения:

U„W = ^„^Т/'Л^Ц expf-,^1

V z_n ) 2z_n

где Ji^ ^— функция Бесселя первого порядка.

Искомую функцию фазы ДОЕ Дг^, фокусирующего в набор кругов с постоянными интенсивностями, с заданными радиусами и расположенных вдоль оптической оси на требуемых расстояниях z_m можно искать в виде суммы с неполностью определенными коэффициентами:

е'7^ ^ '^С^а/Эехрр^^ +ш<р]

где С_п — постоянные, модуль которых задается с учетом выбора интенсивностей /_п, а фаза является свободным параметром,

п к

^п--- , Рп =--- zn         2z„

Из уравнения (36) следует выражение для расчета коэффициентов:

R 2л

С„ = ^"'J J ^т^ У1(а„г)ехр[-/|Злг2 -шф]г2 dr dф            (37)

о о

R

W = 27tJj²(a„r)-rdr .

о

Уравнения (36)—(38) позволяют получить итеративный алгоритм расчета функции фазы ДОЕ, аналогичный алгоритму (24)—(26).

3. Фокусировка в набор осевых точек.

Нетрудно получить разложение аналогичное (36) для расчета много фокусных дифракционных линз, которые формируют вдоль оптической оси z заданное число фокусов на требуемых расстояниях и с заданной интенсивностью. Другие подходы к расчету ДОЕ типа многофокусных линз рассмотрены в [11,12].

В данном случае вместо уравнения (31) для фокусировки в набор кругов следует использовать уравнение для фокусировки в набор дельта—импульсов:

Л(Р) = >/Л5(Р)                            (39)

Тогда вместо уравнений (35) и (36) получим, соответственно:

к 1—       кг"

_е.г(,.Ф) ₌ ^^ ехррр/ +/лф], Р„ = ^ “ ^{L          J} Zz_n

Вместо уравнения (37) коэффициенты суммы (41) вычисляются по формулам

С„ = (л^²) ' J | е'^Г(г,ф) exp -I ^— - т^ 0 0           L ^„

•rdrdcp

Из уравнения (42) видно, что коэффициенты С_п вычисляются с помощью двумерного преобразования Фурье.

Заметим, что вместо суммы (41) для итеративного расчета многофокусных линз можно использовать более простое только радиальное уравнение

N е'гм=^С„ехр[-/р/2]

И=1

Но гауссовые экспоненты в уравнении (43) будут ортогональны только при условии:

R jexp[-/(P„ -P„)r2] rdr = 6„ о

которое выполняется пои

_ -1 _^2

2п П Z0’ Z0

Из (45) следует, что разложением (43) удобно пользоваться для вычисления фазы ДОЕ, если требуемые фокусы расположены только на определенных расстояниях z_n.

4. Фокусировка на поверхность вращения.

Расчет ДОЕ, фокусирующих лазерное излучение на поверхность тела вращения, ось которого совпадает с оптическою осью, был осуществлен методом геометрической оптики в [6].

Ниже рассматривается дифракционный итеративный алгоритм. Если тело вращения с осью z представить как набор его поперечных сечений, то его поверхность аппроксимируется набором колец. Поэтому для расчета ДОЕ, формирующего набор световых колец с заданными радиусами р_п и расположенных на требуемых расстояниях z_n , можно получить уравнение, аналогичное уравнению (36). Для этого вместо выражения (31) для требуемой амплитуды на л—ой плоскости запишем:

A(p.v) = V^-5(p-P„)-e*

Подставив выражение (46) в уравнение (30), получим вместо соотношения (35) следующее выражение для комплексной амплитуды в плоскости ДОЕ:

^('•,<₽) = —7Лл[—1 exp -'^(г² + р²)+;пф ^z. V ^z. J L ^2z„

Обпединяя под знаком постоянной С_п сомножители в уравнении (47), которые не зависят от переменных г и (р, получим вместо уравнения (36), следующее уравнение

^Иг'^ = £СлУДа/)ехр[-ф/2 +/лф]

коэффициенты которого находятся по формулам, аналогичным (38) и (39):

R 2л

С„ ⁼ ^ J J ^е'^Г(Г’^{Ф) J}" ^^ ^РрР/ - ™ф] • Г d г d Ф             (49)

о о

R

^. = 2”$^ (а/)-г dr

О где Jn(x) — функция Бесселя п-го порядка.

С целью ускорения расчетов вместо разложения (48) можно использовать на практике следующее уравнение е‘т(,) = £ С„ J0(a/) ехр[-,’Р/ ]                       (50)

П=1

Однако при этом слагаемые в уравнении (50) в общем случае не ортогональны между собой. Чтобы найти условие, которое надо наложить на параметры ал и рл для достижения ортогональности слагаемых в уравнении (50), можно использовать следующий справочный интеграл [13]:

Г i»¹ 7 Ч Т / Ч Л ¹             -к . Ь² + С² VK

Ie J^bx)J^cx)xdx = — J„ — е , h = —---—

*                      2а V2av          4а 2

Для функций, входящих в уравнение (50), вместо (51) получим

J 4 (a/M (“Z) ехр[-'(Р. - Р^У^ d г =

О

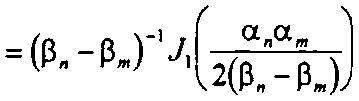
ехр

. «п+а

-I—---

4(в„-в„) •

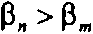
Из уравнения (52) следует, что при удовлетворении параметров ал и рл условию

а а

____ ^{n w} — у

2(Р„-Р„) '

n^m-X.N, p = \,N2

где у_р — корни функции Бесселя: Jibp^O, слагаемые в сумме (50) будут ортогональны и коэффициент! можно рассчитывать по формулам:

R

C^^'^'^J^a^exp^/yrdr            (54)

О

R

^n = 27tjj2(anr)rdr о

Условие (53) ограничеваст выбор значений расстояний z_n и радиусов колец р_л. Однако, как показал численный эксперимент, можно получить хорошие результаты, считая слагаемые в уравнении (50) ортогональными и используя для расчета коэффициентов формулу (54).

• 4.1.    Численные результаты.

Численные результаты, приведенные ниже, относятся к случаю фокусировки на поверхность вращения. Фаза ДОЕ при этом рассчитывается с помощью итеративного алгоритма, основанного на уравнениях (50) и (54). Рассчстные параметры: Л=1 мм -радиус ДОЕ, /с= 104 мм-1, л=256 — число отсчетов по радиальной переменной.

Коническая поверхность описывалась уравнением

Р„ =a(z„-zo) + Po где а=±5х10 3, Z(j= 100 мм, ^z=5 мм — расстояние между плоскостями сечениями конуса, /7=1,10. На рис.З показана полутоновая по уровню 2л фаза ДОЕ (а) и ее радиальное сечение (б), рассчитанные за 10 итераций алгоритмом на основе уравнений (50),(54).

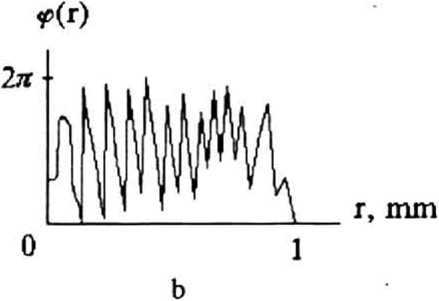
Рис.З Фаза (а) и ее радиальное сечение (б) для ДОЕ, фокусирующего на поверхность расходящегося конуса.

На рис.4 показаны распределения интенсивности (верхняя строка) и их сечения (нижняя строка), сформированные ДОЕ с фазой, показанной на рис.З, и рассчитанные на разных плоскостях вдоль оси z в диапазоне [100 мм, 150 мм] с шагом 10 мм (z растет слева направо).

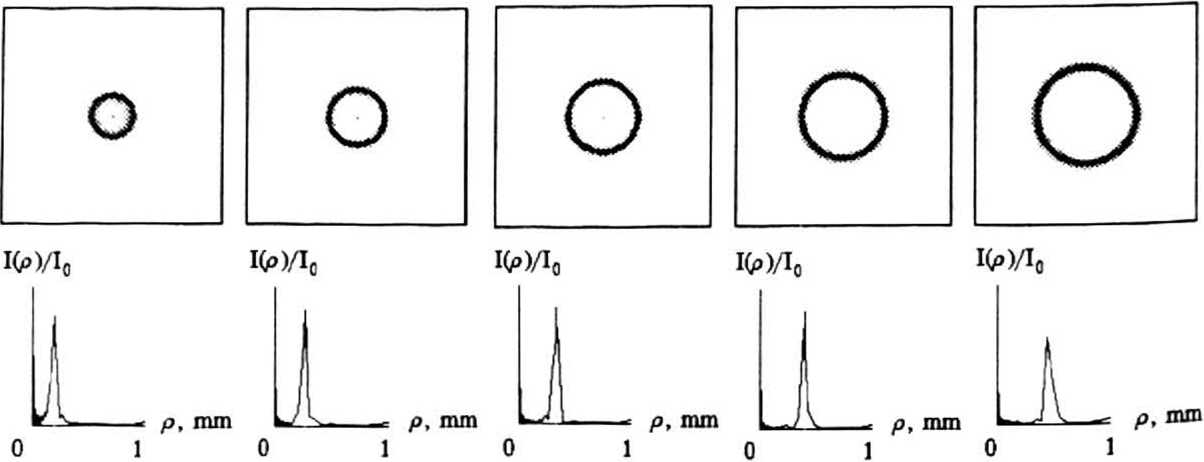
Рис.4 Распределения интенсивности (верхняя строка) и ее радиальное сечение (нижняя строка), сформированные ДОЕ с фазой, показанной на рис.З.

На рис.5 показана зависимость нормированной интенсивности на поверхности конуса (рис.4, а>0) вдоль оси z. кривая 1 - заданное распределение интенсивности, кривая 2 — рассчитанная.

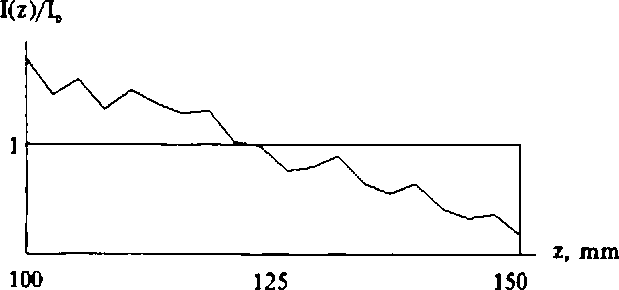
Рис.5 Распределение относительной интенсивности на поверхности расходящегося конуса.

На рисунках 6—8 представлены аналогичные расчетные результаты для фокусировки на поверхность конуса , но при а<0. На рис.6 показана фаза ДОЕ (а ) и ее сечение (б), полученное за 7 итераций по методу (50), (54).

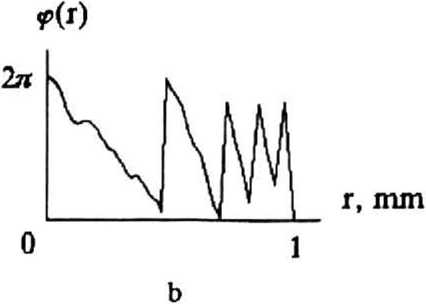
Рис.6 Фаза (а) и ее радиальное сечение (б) для ДОЕ, фокусирующего на поверхность сходящегося конуса.

На рис.7 показаны распределения интенсивности (верхняя строка) и их сечения (нижняя строка), рассчитанные при тех же значениях z_n , что и на рис.4.

1О)Дс

^)До

Му

О 1

1(р)До

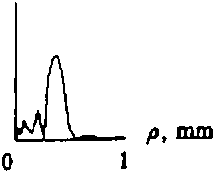
0            1

Цр)До

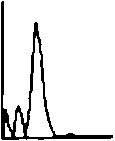
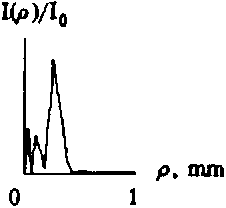
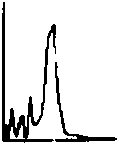
Рис.7 Распределения интенсивности (верхняя строка) и ее радиальное сечение (нижняя строка), сформированные ДОЕ с фазой, показанной на рис.6.

На рис.8 представлен график зависимости интенсивности на поверхности конуса (рис.7, а<0) вдоль оси z: кривая 1 — заданное распределение, кривая 2 — рассчитанное.

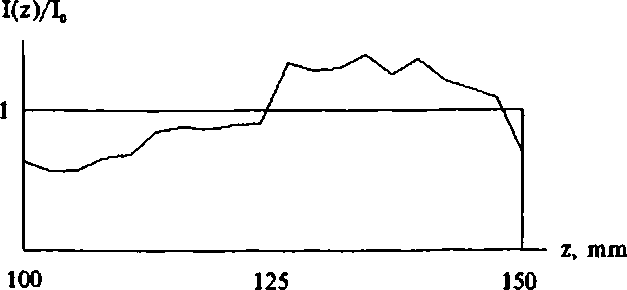
Рис.8 Распределение относительной интенсивности на поверхности сходящегося конуса.

На рисунках 9—11 приведены результаты численного экперимента для фокусировки в цилиндр радиусом р^= 0.5 мм. На рис.9 показана фаза ДОЕ (а) и ее сечение (б), рассчитанные за 10 итераций по формулам (50) и (54) при а=0.

^(г)

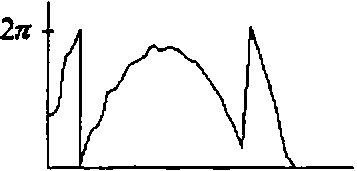
0                       1

Рис.9 Фаза (а) и ее радиальное сечение (б) для ДОЕ, фокусирующего на поверхность цилиндра.

На рис. 10 даны распределения интенсивности и их сечения, рассчитанные на тех же плоскостях, что и для рисунков 4 и 7. Расчет проводился с помощью интегрального преобразования Френеля, которое, в свою очередь, рассчитывалось с помощью алгоритма быстрого преобразования Фурье.

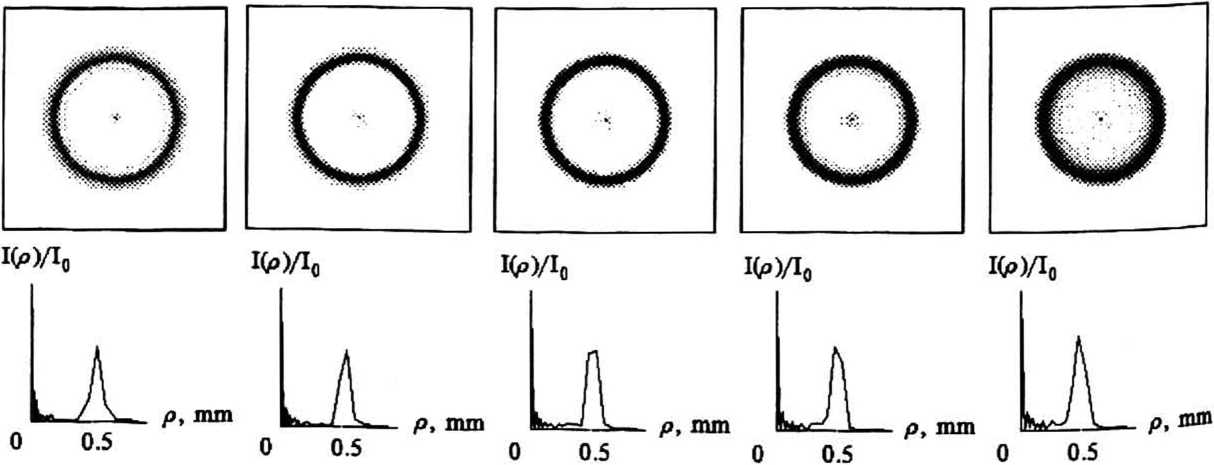
Рис. 10 Распределения интенсивности (верхняя строка) и ее р ад иальное сечение (нижняя строка), сформированные ДОЕ с фазой, показанной на рис.9.

На рис. 11 показан график зависимости относительной интенсивности света на поверхности цилиндра от расстояния z до оптического элемента.

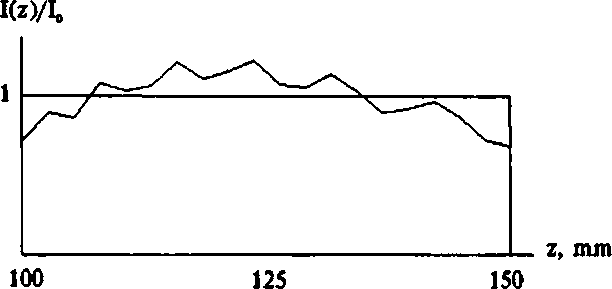
Рис. 11 Распределение относительной интенсивности на поверхности цилиндра.

Приведенные результаты показывают возможность использования предложенных итеративных алгоритмов для расчета фазовых оптических элементов, фокусирующих лазерное излучение на поверхности тел вращения.