Интерференция спиновых и туннельных щелей в квантовом магнитотранспорте двойной квантовой ямы N-NGaAs/ GaAs

Двойная квантовая яма (ДКЯ) - перспективный объект для исследования многоэлектронных явлений в (квази)двумерных системах, поскольку здесь существует два типа межэлектронных корреляций: внутри слоя и между слоями, и соотношение между ними можно менять, изменяя параметры ДКЯ [1]. Наличие межслойных корреляций создает новые условия для существования электронных фаз [2] вплоть до формирования стабильного эк-ситонного конденсата Бозе-Эйнштейна [3]. Интерес к гетеросистеме InжСai-2;As/GaAs обусловлен тем, что в дополнение к связанной с наличием двух слоев псевдоспиновой степени свободы здесь может быть достаточно сильно и стабильно выражена еще одна - спиновая - степень свободы, поскольку объемный g-фактор входящего в твердый раствор InAs в 35 раз превышает таковой для GaAs, формирующего квантовые ямы в традиционной гетеросистеме GaAs/AlGaAs. И хотя эта разница будет меньше в твердом растворе InжСа1-жАз, исследования в этой системе остаются актуальными, поскольку наличие существенных спиновых расщеплений может еще более расширить круг необычных свойств ДКЯ [4]. В нашей предыдущей работе [5] кратко описано немонотонное поведение с наклоном поля минимума магнитосопротивления с небольшим фактором заполнения v = 3, который изначально, в перпендикулярном поле, соответствует спиновой щели. Немонотонность объяснена тем, что щель с порядковым номером 3 из спиновой трансформируется в туннельную, а эти две щели противоположным образом реагируют на параллельную слоям компоненту поля Вц. Здесь мы продолжаем изучение поведения с наклоном поля щелей между магнитными уровнями и экспериментально показываем, что туннельные щели между уровнями с достаточно большими номерами в наклонном поле осциллирующим образом меняются с ростом поля в соответствии с теоретическими представлениями [6].

Мы исследуем магнитосопротивление (МС) ржж и ржу двойной квантовой ямы п-IпжСаі-жАб/СаAs (х ~ 0.2). В исследуемой системе квантовые ямы InGaAs имеют ширину 5 нм, ширина барьера GaAs составляет 10 нм, структура 5 легирована симметрично в прилегающих к двойной квантовой яме барьерах на расстоянии 19 нм от гетерограниц, изначальная полная концентрация электронов 2.1 • 1015 м-2. Подсветка ИК-излучением позволяет увеличить концентрацию носителей более чем в 2 раза. При этом подвижность электронов при низких температурах увеличивается от 1 до 2.7 м2/Вю. На рис. 1 представлены профиль потенциала исследуемого образца, два наинизших уровня энергии, отвечающие симметричному и антисимметричному состояниям, их волновые функции, а также уровень Ферми в исходном состоянии образца.

Рис. 1. Профиль потенциала, (жирная линия) и волновые функции (топкие кривые) исследуемого образца п-1 n₀.2Ga₀.8As/GaAs с двойной квантовой ямой (Ер - уровень Ферми, E_s - уровень симметричного состояния, A sas ~ туннельная щель)

Изменения в структуре осцилляций с наклоном поля в образце до и после предельной засветки представлены на рис. 2. Чтобы проанализировать эти особенности, были рассчитаны магнитные уровни ДКЯ в наклонных полях (рис. 3). При этом мы считали, что величина. g-фактора не меняется с наклоном поля [7]. Анизотропия (/-фактора может ощутимо проявляться в валентной зоне двумерных слоев [8]. Однако эксперименты в наклонных полях на. двумерных слоях родственного нашему материалу InAs с электронной проводимостью [9] хорошо описываются без привлечения анизотропии д. Ранние расчеты в квазиклассическом приближении могли объяснить некоторые особенности квазидвумерного HgTe в наклонных полях [10-12], однако осталось множество неразрешенных вопросов, например, те, что связаны с эффектами магнитного пробоя, которые могут быть объяснены только качественно, но не могут быть включены в эти упрощенные расчеты [13]. Все расчеты, представленные в этой статье, основаны на полном квантовом подходе при учете влияния перпендикулярной компоненты магнитного поля В ±[14] и получены посредством численной диагонализации соответствующих гамильтонианов в матричной форме для систем ДКЯ в наклонном магнитном поле. В этих расчетах автоматически учитываются эффекты, связанные с магнитным пробоем. Расчеты для ДКЯ с симметричным потенциалом были выполнены в точности по работе [14], а. возможная асимметрия ДКЯ была, смоделирована, в первом порядке теории возмущений добавлением линейной зависимости энергии от z к диагональным матричным элементам. Параметры зоны проводимости In_ЖСаі_-жАв при ж = 0.2, использованные в расчетах: эффективная масса m*/m о = 0.058; (/-фактор \д( = 1.2, полученный интерполяцией из зонных параметров GaAs и InAs [15] в предположении их линейной зависимости от х. В расчетах использовалась величина туннельной щели в отсутствие поля A sas ⁼ 4 мэВ, полученная из ранее проведенных оценок.

Радикальное различие в осцилляционном поведении с наклоном поля в InGaAs/GaAs ДКЯ в сравнении с традиционной GaAs/AlGaAs ДКЯ может быть прослежено на. рис. 2. В GaAs/AlGaAs нечетные особенности исчезают с наклоном, таким образом демонстрируя их связь с туннельными щелями и то, что туннельные щели являются наименьшими щелями на. картине магнитных уровней, соответствующей диапазону осцилляций, рассмат- риваемых в [16]. В нашей системе ДКЯ, напротив, эти особенности усиливаются: смотри минимум для v = 3 на рис. 3. Различие имеет место, несмотря на ту же величину Asas в нашей системе ДКЯ, что и в типичной GaAs/AlGaAs. Таким образом, в нашем случае нечетные особенности связаны со спиновыми щелями, и спиновые щели являются наименьшими в слоях InGaAs наших структур. Это несмотря на то, что объемный g-фактор в InGaAs больше, чем в GaAs. Известно, что спиновые щели в материалах с высокой подвижностью могут увеличиваться вследствие обменного взаимодействия при соответствующих значениях фактора заполнения [17]. Так как подвижности в структурах GaAs/AlGaAs обычно намного больше, чем в наших слоях InGaAs, такое усиление эффективного g-фактора в первом случае больше, чем во втором, хотя для объемных значений имеем обратное отношение.

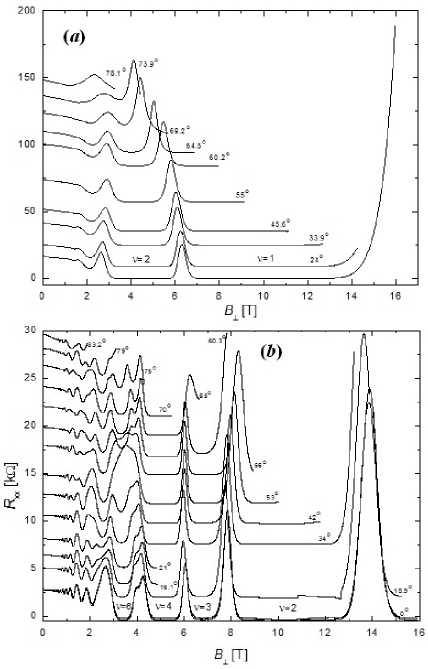
Рис. 2. Магнитосопротивление р_хх{ В±,Вц) при разных углах наклона поля (а) до освещения и (Ь) после предельного ИК-освещепия

Выделим следующие особенности в эволюции сложной картины осцилляций с наклоном поля и проанализируем их на основе проведенных расчетов: (i) плавное немонотонное изменение минимума при v = 3 после предельной засветки образца; (11) резкие и немонотонные трансформации минимума для фактора заполнения v = 6 в том же состоянии образца.

Как отмечено выше, нечетная особенность с v = 3 в перпендикулярном поле соответствует спиновой щели (рис. За), и добавление Вц приводит к ее увеличению. Однако под действием той же Вц одновременно происходит подавление туннельной щели. В результате, согласно представленным здесь одноэлектронным расчетам, при фиксированном наклоне образца в некотором поле спиновая щель и туннельная должны сравняться, вследствие чего щель для v = 2 должна закрыться (рис. 2b-d). Точка закрытия этой щели смещается в меньшие Вд с ростом наклона. После прохождения этой точки изменяется природа щели для v = 3: теперь ей соответствует убывающая с ростом поля туннельная щель. Что и объясняет наблюдаемое немонотонное поведение данной особенности. Наклон, при котором наблюдаются наиболее сильные проявления особенностей МС v = 3, соответствует совпадению величин спиновой и туннельной щелей. У нас это имеет место между Ө = 53° и 60° (рис. ЗЬ и с). Следует отметить, что в наших экспериментах нет указаний на полное закрытие щели v = 2 в данном состоянии образца (рис. 2Ь, хотя для более подробного исследования поведения щели v = 2 нужны поля больше имевшихся в 18 Т). Для объяснения этого факта, вероятно, недостаточны представленные здесь одноэлектронные расчеты, а многочастичные эффекты могут привести к антикроссингу в месте ожидаемого закрытия щели v = 2 [18]. что. однако, не отменяет пемопотошюго поведения щели v = 3. Устойчивая тенденция к закрытию щели v = 2 хорошо видна на неосвещенном образце, когда все особенности смещены в существенно меньшие поля (рис. 2а).

Рис. 3. Немонотонное поведение с наклоном поля минимума МС с v = 3 и его анализ на основе рассчитанных уровней (в одноэлектронном рассмотрении). На вставках: экспериментальные записи вокруг v = 3, сопоставленные с соответствующим фрагментом рассчитанной картины уровней. Угол Ө : 0 (а), 53°(Ь), 60°(с), 65°(d)

Резкие трансформации особенностей с v = 6 также обусловлены воздействием Вц на туннельную щель. С тем, однако, отличием, что соответствующая v = 6 туннельная щель не только закрывается при определенном сочетании угла наклона Ө и Вд, но затем открывается при дальнейшем возрастании одного из этих параметров. Тогда как туннельная щель для v = 2, располагающаяся между двумя уровнями Ландау с АУ = 0, только стремится к нулю при Вд ^ то и Ө = 0. Как следует из расчетов, следующие за закрытием открытия туннельной щели, то есть ее осциллирующее поведение, имеют место для Nl > 1 (рис. 3b d), притом количество соответствующих закрытию туннельной щели узлов возрастает с ростом Nl- Осциллирующее поведение туннельной щели можно объяснить эффектом интерференции Ааронова-Бома между состояниями электрона в двух слоях под действием Вц[6]. Момент закрытия щели для v = 6, как это следует из наших расчетов, и сопоставление картины уровней с экспериментальной кривой при соответствующем угле Ө = 63° представлены на. рис. 4. При увеличении наклона, (рис. 2Ь) минимум при v = 6 возрождается. Это согласуется с расчетами (рис. 3b d), поскольку узел пересечения уров- ней с Nl = 1 смещаете я в меньшие В л с ростом наклона. При больших углах наклона по обе стороны от минимума МС для v = 6 хорошо видны спиновые расщепления, усилившиеся по сравнению с перпендикулярным полем вследствие добавления компоненты Вц. Согласно рассчитанной картине уровней осциллирующее поведение туннельной щели должно воспроизводиться в картине осцилляций МС при больших v с периодом 4. И, действительно, немонотонные транформации осцилляций с наклоном можно выделить в окрестностях v = 10 (рис. 2Ь), притом превращения минимума в максимум наблюдаются дважды, в согласии с ожидаемым наличием двух узлов между уровнями с NL = 2. Однако в меньших полях В^ разрешение осцилляций уже хуже, что затрудняет детальный анализ.

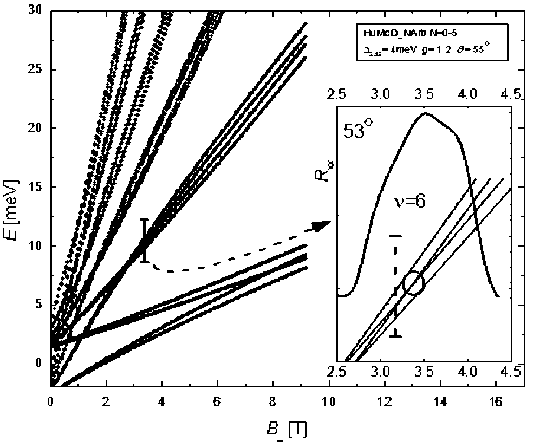
Рис. 4. Картина магнитных уровней при угле наклона Ө = 53°, сопоставленная с локальным превращением минимума р_хх с v = 6 в максимум

3.    Заключение

Выявлено сложное поведение осцилляций магнитосопротивления с наклоном магнитного поля в ДКЯ в гетеросистеме Ino.2Gao.8As/GaAs, отражающее изменения туннельных щелей с величиной наклоненного поля в согласии с рассчитанной эволюцией картины магнитных уровней. Показано, что в наклонном поле в области больших номеров Ландау туннельные щели осциллируют с полем. При малом факторе заполнения v = 3 наблюдаются только немонотонные изменения интенсивности минимума МС, поскольку соответствующая щель немонотонно меняется с наклоном поля, превращаясь из спиновой в туннельную. Таким образом, одноэлектронная модель расчетов адекватно описывает основные тенденции поведения осцилляций в ДКЯ с наклоном поля, хотя некоторые особенности требуют более подробного многоэлектронного описания.

• *Работа доложена на 5-й Всероссийской конференции молодых ученых «Микро-, нанотехнологии и их применение» им. Ю.В. Дубровского, ИПТМ РАН, Черноголовка, 19—22 ноября 2012 года.