Интерференционная схема для генерации поляризационно-неоднородного лазерного излучения с использованием пространственного модулятора света

Цилиндрические (с аксиальной симметрией) векторные пучки имеют множество приложений, включая микроскопию, литографию, ускорение электронов, обработку материалов, высокоразрешающую метрологию, микроэллипсометрию и спектроскопию. Подробный обзор приведён в работе [1].

По сравнению с обычной (линейной или круговой) поляризацией радиально-поляризованный пучок имеет удвоенную эффективность при резке металлов [2], а также неоднородно-поляризованные пучки дают возможность управления процессами лазерной абляции [3, 4], повышения разрешения в задачах микроскопии [5, 6] или создания сложных периодических поверхностных структур, индуцированных лазером [7]. Кроме того, радиально-поляризованные пучки могут применяться для передачи информации [8].

Существуют два принципиальных способа получения осесимметрично поляризованного излучения: внутрирезонаторный и внерезонаторный. В первом случае в составе резонатора используют поляризационно-селективные оптические элементы [9]. Этот метод является предпочтительным для мощных лазеров, обычно имеющих высокий коэффициент усиления активной среды, низкую добротность резонатора и относительно низкое качество излучения. Однако для метрологических и иных применений, требующих высокого качества пучка, эти методы малопригодны.

Главным преимуществом внерезонаторных методов формирования поляризационно-неоднородных мод является универсализм. Среди этих методов можно выделить однопучковые, в которых формирование нужного поляризационного состояния достигается либо за счёт пропускания пучка через анизотропный кристалл [10– 12], в котором происходит интерференция обыкновенных и необыкновенных лучей, либо за счёт управляемого поворота плоскости поляризации по сечению пучка при помощи секторных пластинок [13, 15] или интерференционного поляризатора [16– 18]. Данные методы, как правило, предназначены для какой-то определённой длины волны, например 1530 нм [17], и их перестройка весьма трудоёмка. Многопучковые методы основаны на когерентной суперпозиции пары различных мод, например, с помощью классического интерферометра [19]. Таким способом можно формировать любые типы векторных пучков, и, в принципе, такой метод применим для любой длины волны. Методы разделения пучков в интерферометре и их сложения могут варьироваться. Например, в работе [20] разделение пучков осуществляется при помощи бинарного ДОЭ с несущей частотой в парных порядках дифракции, а соединяются пучки обычным, неполяризующим све- тоделительным кубиком. В работе [21] разделение пучков осуществляется по фронту за счёт расположенных на определённом расстоянии друг от друга во входной плоскости Фурье-каскада двух ДОЭ, а соединение происходит после прохождения линзы в выходной плоскости Фурье-каскада на дифракционной решётке, период которой подобран так, чтобы обеспечить параллельность пучков после соединения. Возможен и смешанный вариант [22], когда два элемента расположены рядом и производят встречные пучки без линзы, за счёт несущей, а дальше в месте пересечения пучков также ставят дифракционную решётку для соединения пучков. Все перечисленные методы обладают одним общим недостатком, а именно сложной перестройкой на другие типы поляризаций и, в случае фазовых ДОЭ, на другую длину волны. Для этого необходимо заново изготавливать 2–3 ДОЭ и юстировать схему. Кроме того, потери энергии при соединении пучков на дифракционной решётке больше, чем на кубике и даже теоретически при использовании бинарной фазовой решётки не могут быть меньше 60%. Все это заставляет искать пути развития интерферометрических схем. В настоящей работе предложено использовать пространственный модулятор света (ПМС, SLM) для формирования пучков в интерферометре, а объединять пучки при помощи кубика. Отметим, что светоделительный кубик, в отличие от решётки, даёт два пучка равной мощности с необходимым поляризационным состоянием, причём оба могут быть использованы.

1.    Обоснование предложенной схемы экспериментальной установки

Идея использования ПМС для формирования заданного поляризационного состояния появилась достаточно давно, например, в работах [23–26] предложены схемы без разделения пучка (по нашей классификации однопучковые). Разрешение и энергетическая эффективность таких методов пока не очень высокие. В работе [27] реализована схема, в которой для разделения пучков используются парные дифракционные порядки, а объединение производится при помощи светоделительного кубика, то есть фактически в схеме [20] стационарный ДОЭ заменён на ПМС. Так же, как и в схеме [20], при помощи ПМС формируются комплексно сопряжённые вихревые пучки, единственное отличие состоит в том, что для создания пары неоднородно-поляризованных пучков использованы наложенные голограммы, дающие угловое разделение пучков. Недостатки у такой схемы те же, что и у схемы [20] – невозможность формирования других поляризационных состояний, кроме радиальной, азимутальной и смешанной поляризаций первого порядка. Что касается формирования нескольких выходных пучков, то схема [20] тоже производит два выходных пучка под прямым углом, и применение наложенных голограмм оправдано, лишь если требуется больше, чем два пучка.

В работе [28] предложена подобная [27] схема для генерации неоднородно-поляризованных пучков с участками эллиптических поляризаций. Разделение и формирование сопряжённых пучков также осуществляется в парных дифракционных порядках после прохождения лазерного пучка через сформированную на ПМС фазовую голограмму с косинусоидальной несущей. Далее, с помощью линзы в фокальной плоскости получают Фурье-образы пучков, каждому из которых придаются необходимые поляризации с помощью волновых пластинок. После прохождения второй линзы два пучка вновь соединяются в фокальной плоскости и производится компенсация углов распространения при помощи дифракционной решётки. Период решётки при этом должен быть точно таким же, как и период несущей на исходной голограмме. Предложенная схема представляет собой «гибрид» схем из [20, 22]. Основными преимуществами данной схемы являются простота и компактность, а также легкость юстировки и малая чувствительность к вибрациям. Однако, наряду с достоинствами, такой вариант схемы обладает и всеми недостатками, упомянутыми во введении. Следует также отдельно отметить, что даже небольшие отклонения периода решётки от требуемого приводят к существенной погрешности формирования пучка. В идеале решётку тоже следовало бы формировать при помощи ПМС, но такой путь является весьма затратным. И, наконец, самым существенным недостатком как [27], так и [28] являются ограниченные возможности формирования различных типов поляризаций и различной амплитуднофазовой структуры пучков. По сути, из-за формирования пары пучков фактически одним ДОЭ путём использования парных дифракционных порядков для сложения могут быть сформированы лишь комплексно-сопряжённые пучки с одинаковыми амплитудными распределениями. Преодолеть указанное ограничение можно, используя для формирования каждого пучка свой ДОЭ, что приводит к принципу разделения пучков по фронту волны, описанному в [21, 22]. Теперь, на новом техническом уровне, нет необходимости устанавливать два отдельных ДОЭ, как это было в [21, 22], поскольку площади современных ПМС позволяют разместить на них всё необходимое с нужными расстояниями между элементами. Роль двух ДОЭ с использованием ПМС могут выполнять различные его участки. Разделив эти пучки пространственно, возможно осуществлять перестройку поляризационного состояния и при их совмещении получать векторные лазерные пучки. В нашей работе предложена схема с одним ПМС и без дополнительных линз. Потребность в дополнительных линзах устраняется за счёт включения в схему интерферометра Маха–Цендера в полной конфигурации. Следует заметить, что многие ПМС предназначены для работы в первом порядке дифракции из-за довольно существенных помех, создаваемых в нулевом поряд- ке по причине недостаточной дифракционной эффективности. Предложенная схема интерферометра позволяет легко комбинировать нужные порядки дифракции за счёт настройки. В оптической схеме детально ход лучей не показан, но за счёт наклона зеркал и светоделителей можно совмещать нужные порядки дифракции. При этом в каждом плече распространяются одновременно моды, сформированные обоеми частями ПМС, но на выходе наклоны зеркал и светоделителей обеспечивают пространственное и угловое совмещение только +1 порядка от левой части ПМС и –1 порядка от правой части ПМС. Остальные порядки распространяются с таким угловым и пространственным отклонением, что они не регистрируются. Оптическая схема приведена на рис. 1.

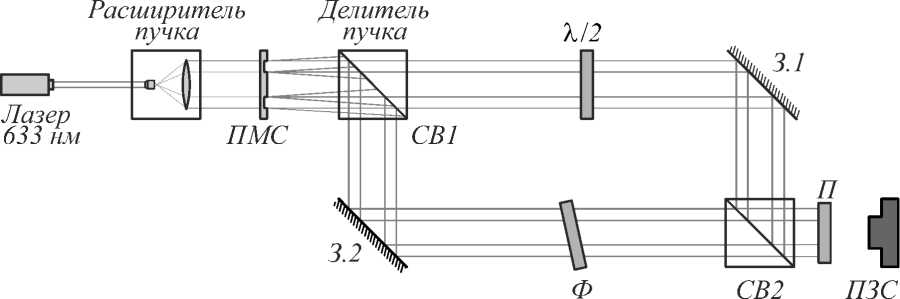
Рис. 1. Интерференционная схема для генерации поляризационно-неоднородного лазерного излучения с использованием пространственного модулятора света

Излучение лазера с длиной волны 632,8 нм расширяется коллиматором, состоящим из микрообъектива 20×, пинхола с отверстием 10 мкм и выходного объектива с фокусным расстоянием 1 м, таким образом, чтобы выходное излучение равномерно освещало всё рабочее пространство ПМС. Далее, проходя ПМС, лазерный пучок приобретает необходимые модовые составляющие, и формируются порядки дифракции. Светоделитель разделяет падающее излучение на два плеча интерферрометра Маха–Цендера, в левом плече которого расположена пластинка λ /2, изменяющая поляризационное состояние. Положением зеркала З.1 осуществляется настройка угла распространения пучка таким образом, чтобы на светоделитель СВ2 порядок +1 от левой части ПМС падал в центр. Аналогично поступаем для –1 порядка от правой части ПМС, распространяющегося в правом плече интерферометра, добиваясь падения излучения в ту же точку кубика, куда падает и излучение от левого плеча интерферометра. При прохождении светоделителя СВ2 излучение от правого плеча проходит, не изменяя угла, в сенсор ПЗС. Угловым распространением излучения от левой части модулятора можно управлять, изменяя угол поворота светоделителя СВ2. Таким образом на светоделителе СВ2 осуществляется сложение мод и формирование векторного пучка. Для подстройки разности фаз в одном из плеч интерферометра в схему добавлена кварцевая пластинка Ф. Распознавание поляризационных состояний пучка осуществлялось поляризатором П, расположенным непосредственно перед ПЗС.

2.    Формирование и исследование неоднородно поляризованных пучков

Для проверки работы описанной оптической установки вначале в соответствующих секциях ПМС формировались моды Гаусса–Эрмита (0, 1) и (1, 0). Формирование осуществлялось в первом порядке дифракции путём формирования фазового ДОЭ [29] с пилообразной несущей [30–32]. Полутоновое изображение фазы показано на рис. 2.

Рис. 2. Изображение фазы, выводимой на SLM для генерации поляризационно-неоднородного лазерного излучения

На рис. 3 приведено изображение распределения интенсивности на регистрирующей матрице, в начале одного из плеч интерферометра, где не произведено совмещения мод. Причём кадр ограничен таким образом, что в него попадает +1 порядок от одной половины модулятора, нулевой порядок и –1 от другой половины модулятора. Видно, что разные половины модулятора формируют образы разных требуемых мод. Видно, что формируется довольно интенсивный нулевой порядок дифракции из-за присущих всем ПМС искажений передачи фазы в пределах периода несущей. Но, как известно [29], это явление не приводит к искажениям амплитудно-фазового распределения в полезном первом порядке дифракции.

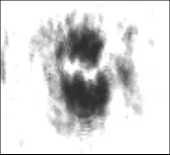
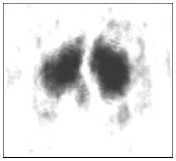
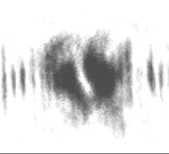
Изображения в выходной плоскости интерферометра, полученные при различных положениях анализатора и без него, приведены на рис. 4. Хорошо видно, что пучок имеет азимутальную поляризацию.

Заключение

Экспериментально исследована новая оптическая схема для формирования векторных пучков. Эксперименты показали применимость модифицированной схемы интерферометра для работы с ПМС. Показано, что такая оптическая система позволяет формировать азимутально поляризованный пучок.

Рис. 3. Изображение в выходной плоскости сгенерированного пучка от +1 и –1 порядков

б)

м

в)

г)

д)

Рис. 4. Распределения интенсивности в выходном пучке в зависимости от положения анализатора 0° (а), 45° (б), 90° (в), 135° (г), изображение в отсутствие анализатора (д)

Работа выполнена при поддержке Министерства науки и высшего образования РФ (МК-1797.2019.2) в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН в части расчёта ДОЭ, гранта РФФИ (№18-29-20045 мк) в части экспериментальных исследований, а также гранта РФФИ (№18-07-01470) в части формирования вихревых пучков.