Интерференционные эффекты при наклонном падении встречных волн на поглощающий слой

Проблема управления отражательной и пропускной способностью планарных структур является достаточно актуальной [1-4]. В средах с комплексным показателем преломления распространение двух встречных когерентных волн сопровождается формированием направленного интерференционного потока (ИП) реактивных компонент волновых полей, величина которого определяется произведением амплитуд и разностью начальных фаз этих волн. Известно, что в случае одиночной волны реактивные компоненты не дают вклада в ее интенсивность. Однако, при наложении реактивных компонент поля двух волн формируется ИП в направлении, где для одиночной волны перенос энергии отсутствует [5, 6]. На вклад ИП в процесс переноса энергии при падении света на границу раздела прозрачной и поглощающей сред указывалось еще в работах [7,8]. Эксперименты по наблюдению ИП в тонких металлических пленках впервые были проведены в работах [9, 10].

Наличие интерференции встречных волн (ИВВ) в поглощающей среде приводит к возникновению пространственных осцилляций выделения тепла в образце, т.е. к интерференционному тепловыделению. В случае падения встречных волн на поглощающий слой можно добиться увеличения или уменьшения тепловыделения за счет изменения энергетических потоков, уходящих от

поверхностей слоя [6, 10-12]. Использование ИВВ особенно актуально для оптимизации режимов СВЧ термообработки и эффективного равномерного нагрева металлических деталей и образцов [13, 14].

В имеющейся литературе рассмотрение особенностей ИВВ проводится лишь для нормального падения волн на плоский слой. Между тем, наклонное падение света на поглощающие покрытия широко распространено на практике и имеет ряд технологических и экспериментальных преимуществ. В отличие от случая нормального падения, при наклонном падении коэффициент отражения зависит от состояния поляризации падающего света [15, 16], что позволяет использовать этот эффект при создании различных поляризационных устройств [17, 18]. В работе [19] наклонное падение используется для оптимизации распределения поглощенной энергии по слоям гетероструктуры фотовольтаической ячейки.

В различных плоско-слоистых структурах на границах раздела сред всегда присутствует пе-реотражение света, что приводит к ИВВ и формированию ИП. Указанное обстоятельство определяет важность теоретического анализа в подобных структурах при наклонном падении на них излучения. В настоящей работе исследуются особенности ИВВ в поглощающем слое при наклонном падении встречных волн на противоположные его поверхности.

• 2.    ОСНОВНЫЕ СООТНОШЕНИЯ

Пусть поглощающий слой с комплексным показателем преломления n= n1- in2 и магнитной проницаемостью μ= 1 ограничен бесконечными плоскостями y = 0 и y = d . Обла- сти у < 0 и у > d представляют собой вакуум. Из вакуума на слой под углом τ падают две встречные плоские волны с частотой ω и линейной s-поляризацией (векторы электрического поля падающих волн перпендикулярны плоскости падения YOZ). Геометрическая хема задачи представлена на рис. 1. Считая временную зависимость всех волновых полей от времени пропорциональной exp(itot), их координатную зависимость определим следующими выражениями:

• E1 = A eXP[i (Фа — k0уУ — k0zz)] ,E0 = B eXP[ i (Фь + k0 уУ + k0 zz)] (1)

Здесь ω – частота, A и B – амплитуды, ϕ _a и ϕ _b – начальные фазы падающих волн, k _{0 у} = k ₀cos t, k _{0 z} = k ₀sin т , k ₀ = to/ c -волновое число и c – скорость света в вакууме. Решение граничной задачи с учетом необходимых граничных условий для волновых полей приводит к следующим выражениям для электрического поля отраженных и прошедших волн в области у <  0

E r = -rA exp[i(m + k. у - k,. z)], ax                           a 0 у         0 z t                                                 (2)

^E bx = ^{tB eX}P[ i ⁽ Ф ь ^{+ k} 0 у У ^{+ k} 0 z z ^)]

и в области у >  d

Ebx = -rB eXP[i(Фь + 2k0yd - k0уУ + k0zz)],

^E a'x = ^{tA eX}P^[ i ^ a — ^k 0 уУ — ^k 0 z z ^)]‘

Здесь введены амплитудные коэффициенты отражения и пропускания:

r = r + ir2 = iG(в2 - 1)sin kd,t = (t1 + it2)exP(ik0у^) = 2eGexP(ik^d),(4)

где введены следующие обозначения:

G = [2 в cos k _y d + i ( в ² + 1)sin k _y d ] ^{- 1} , ^ky = ^ky 1 ^{- ik}y 2 = ^{k cos} П , k = k ₁ - ik ₂ = k ₀ n = k ₀ ( n ₁ - in ₂) , в = cos т / n cos n — для волн s-поляризации (дляволнр-поляризации в = cos n / n cos т ), η – угол преломления. Выражения (4) для коэффициентов r и t при соответствующем выборе начала отсчета совпадают с выражениями, приведенными в [21]. Соотношения для y - и z -компонент магнитного поля падающих и отраженных волн вне слоя определяются стандартным образом с помощью уравнений Максвелла и имеют вид, аналогичный (1 - 3).

Запишем теперь волновое поля внутри слоя ( 0 <  У <  d ):

Qa = AG(1 - в)вn exP[i(ma - kyd)],

• 3.    ПОТОКИ ЭНЕРГИИ ВНЕ И ВНУТРИ СЛОЯ

Рассмотрим формирование энергетических потоков волн во всех трех областях. Выражение для усредненной по времени плотности потока энергии, определяемой вектором Пойнтинга, в области у <  0 имеет вид

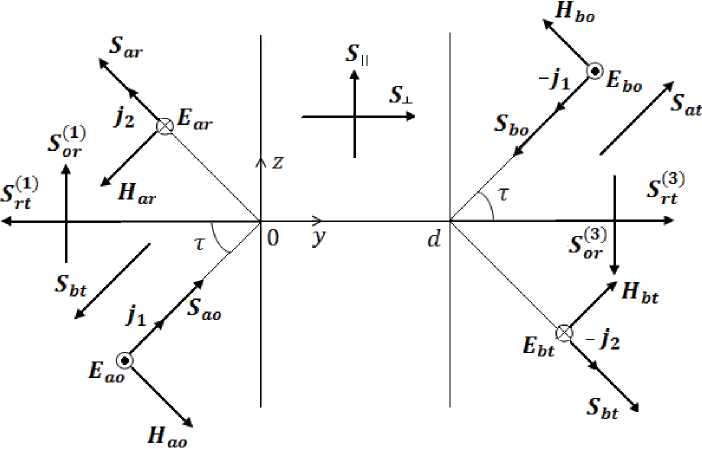
Рис. 1. Схема падения встречных волн на поглощающий слой

5 =—Re[( E* + e; + Eb)( h0 + h; + Hb )*] = 8n(6)

= 50 + 5 r + 5b + 5,0r + 50 * + 5r*, a a b 1            11

где введены следующие составляющие полного потока:

50 = — Re[ E °, H °*] = — A2 j., a                       a                a1

8n8

5 r = — Re[ Er, Hr *] = — RA2 j a q      La ’ aJo•

5 ‘ = — Re[ E *h, H *h *] = -—TB2 b 8n b b8

5 “ * = C- Re([ E _a °, H b * ] + [ E b , H 0* ]) = 0, 8n

5 0 ^r = -c - Re([ E :, H ; * ] + [ E ; , H m =

С ;2Г

= — ^{A [} r ^cos(2 ^у ) - ^r 2 sin⁽² ^у ^)]( J_x + j 2 ), 8 n

5 r*

—Re([ E ; , H b * ] + [ E b , H ; * ]) = 8 n

c

= — AB ^{[( r} 1 * 1 ^{+ r} 2 * 2 )C°^S B ^{- ( r}t 2 ^{- r} 2 * 1 )^Sln B ^]C j 2 ^- J 1 )-8 n

Здесь единичные векторы j ₁ и j ₂ задают направления распространения падающей на слой и отраженной от него волн в области у <  0 , величина 5 = Ф _ь — ф _а + k_o d + 2 k_zz имеет смысл разности фаз падающих волн на двух границах раздела сред. Введенные энергетические коэффициенты отражения и пропускания определяются стандартными соотношениями R = | r | и T = | * | . Аналогично определяется суммарный поток в области у >  d :

5 ₃ = 5 b + 5 b + 5 a + 5 ₃ ^{0 r} + 5 ₃ ⁰ * + 5 r . (8)

Из полученных выше соотношений следует, что при наклонном падении на противоположные стороны слоя плоских встречных волн суммарные энергетические потоки вне слоя складываются из потоков падающей, отраженной и прошедшей волн ( 5 _{a b} , 5 r _b , 5 ba ), а также трех '                            z’ ⁰ r 0 * r *

интерференционных потоков ( 51 3,51 3,51 3 ). Потоки 5 “r коллинеарны оси Zu формируются в результате интерференции падающей и отраженной волн. Потоки 51 3 формируются падающей и прошедшей волнами, в данной геометрии задачи интерференционные потоки 5 103* равны нулю. Потоки 51 r*3 коллинеарны оси Y и формируются отраженной от слоя и прошедшей через него волнами. Модуль каждого из интерференционных потоков определяется произведением амплитуд обеих волн и параметрами слоя.

Внутри слоя ( 0 <  у < d ) интерес представляет нормальная (по отношению к границам раздела сред) компонента полного потока, которая осуществляет перенос энергии через поглощающий слой и определяется следующим образом: S 2 _± = ( С /8 п ) Re( E 2 , • H * _: ) = S ^ + S 2 , + S J,

Я _± = c- Rc{ a c°^s^ [| F ; |‘^e xp( ^— 2 k у , у ) ^—| e a |‘^e xp ⁽² k , , у ) ^— 8 n

- ^Fa Й , ^eX P ^{( — 2 ik}y ! у ) ⁺ Q a F a ^eX P ⁽² ik_{y t} у ^)]} '

Sb_ = A-Re{acos^*[Fb |2 exp( 2к,2у)—|Q, |2 exp(2ку2у)— 8n                                       (9)

^— F b Q * ^ex P( ^— 2 k 1 у ) ⁺ Q b F b exp⁽² i^k _{y l} у ^)]} '

S int =— Re{ a cos ^ *[ F F_b exp( — 2 ik z -2 k у ) - F Q exp( — 2 k z -2 ik у ) + - 8 n               a b          ^{z      у 2}      a^          ^{z у 1}

+ Q, F b exp( — 2 zk , z + 2ik _{y 1} у ) — Q,Q , exp( — 2 ik _z z + 2 k , у у ) + F b F * exp(2 zk _z z — 2 k , у —

^{— F} b Q * ^exp(^{2 i}' ^k z ^{z — 2 ik} , у ) ⁺ Q.F' a ^exp^{(2 ik} z ^{z +} Hk; >  у ) ^— Q b Q * ^ex p(2i ^k _z ^{z + 2 k} y 2 у ).

Выражение для тангенциальной составляющей полного потока внутри слоя имеет аналогичный вид:

S _{2 D} = ( c /8 n )Re( E ₂ , • H * у ) = S * + S ₂ ^b _a + S “, (10) его составляющие ввиду их громоздкости мы не приводим. Здесь и в дальнейшем нормальной составляющей (т.е. y -компоненте) полного и интерференционного потоков для наглядности будем приписывать индекс « ⊥ », а тангенциальной составляющей ( z -компоненте) - индекс « □ ». Из полученных соотношений следует, что полный энергетический поток внутри слоя формируется из потоков проходящих в слой волн и их интерференционных потоков. Отметим, что в поглощающей среде интерференционные потоки возникают не только для однонаправленных, но и для встречных волн.

С точки зрения участия в переносе энергии через поглощающий слой интерес представляет ИП отраженной и прошедшей волн 5 ₁ ^r* ₃ . Поскольку интерферирующие волны падают на слой под равными углами, распространение ИП происходит вдоль нормали к границам слоя. Их единственная y -компонента определяется выражениями:

Sjb = + An AB^RT cos(A* — Ar ± 5)cosr, (11) где j = 1 отвечают верхние знаки, а j = 3 -нижние знаки; Δ t и Δ r – набеги фаз при прохождении и отражении волн. В отличие от 5 ” r rt величины 5 j 3 существенно зависят еще и от разности фаз падающих волн δ . В свою очередь δ определяется разностью начальных фаз падаю- щих волн Δϕba = ϕb - ϕa , толщиной слоя d и углом расходимости отраженной и прошедшей волн. В силу непрерывности тангенциальных компонент векторов поля нормальные компоненты как полного, так и ИП являются непрерывными функциями при переходе через границы раздела сред.

• 4.    ЧИСЛЕННЫЙ АНАЛИЗ

Исследуем в широких интервалах углов падения τ и разности начальных фаз Δϕba = ϕb - ϕa особенности формирования полного и ИП внутри сильно поглощающего слоя. В качестве расчетных были выбраны оптические параметры типичного сильно поглощающего материала – меди [21]: n1 = 0.62 , n2 = 2.57 . Расчеты проводились для границы слоя y = d и координаты z = 0 на длине волны падающего света λ = 58 9 нм при условии равенства амплитуд падающих волн, т. е. A = B . Толщина слоя принималась равной глубине скин-слоя на данной длине волны ds = λ (2πn2) ≈ 36.5нм.

На рис. 2 представлены рельефы зависимостей поперечной S _{2 ⊥} , S ₂ ⁱⁿ _⊥ ^t и продольной

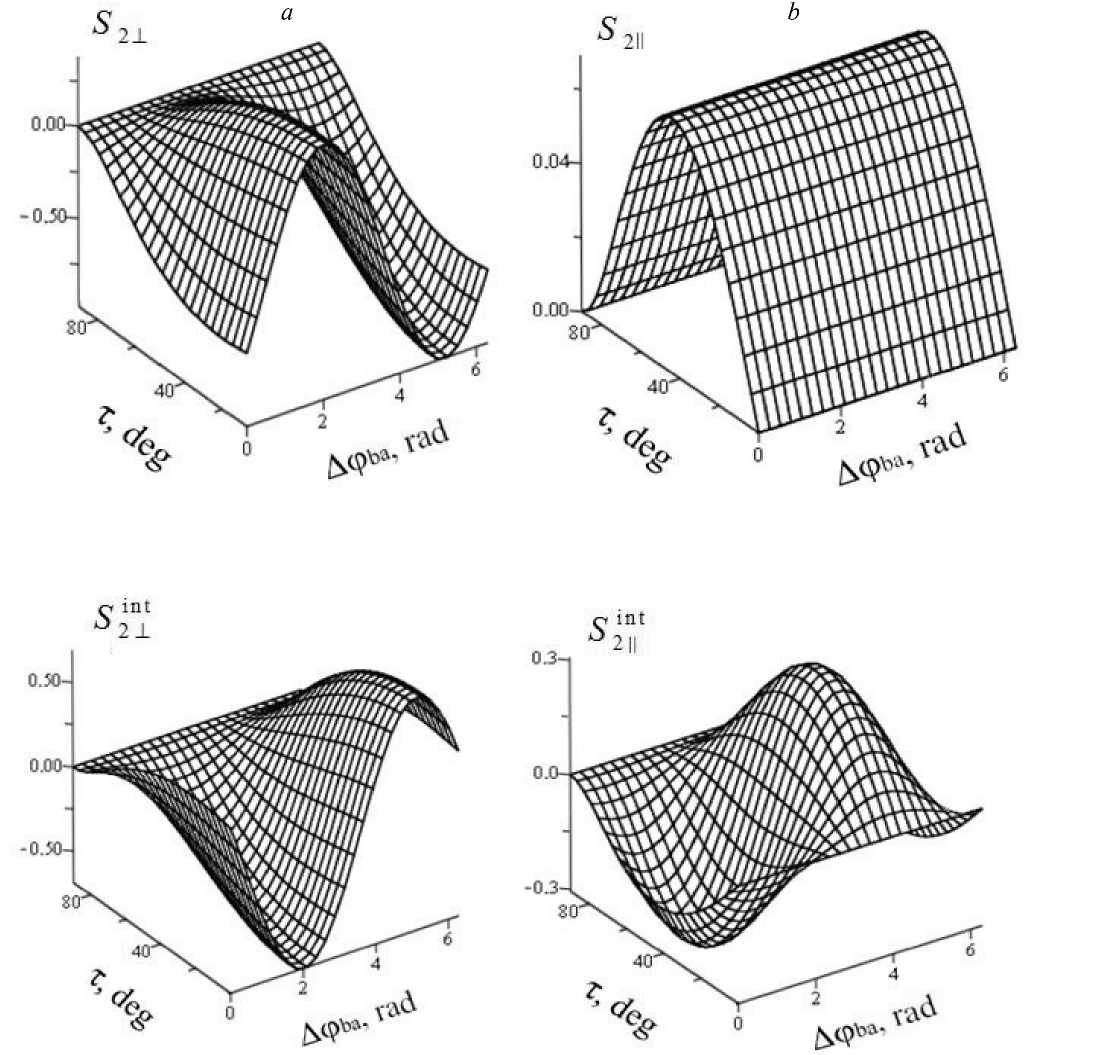
Рис. 2. Зависимость поперечной и продольной составляющих полного и интерференционного потоков внутри слоя от угла падения и разности фаз падающих ТЕ-волн

S 2 □ , S 2njt составляющих нормированных полного и интерференционного потоков внутри слоя от угла падения τ и разности фаз Δ ϕ _ba . Нормировка потоков проводилась на величину S a = ( c 8 n ) A¹ . Из приведенных зависимостей следует, что величина и направление потоков S ₂ ⁱⁿ _⊥ ^t гармонически зависят от разности началь-

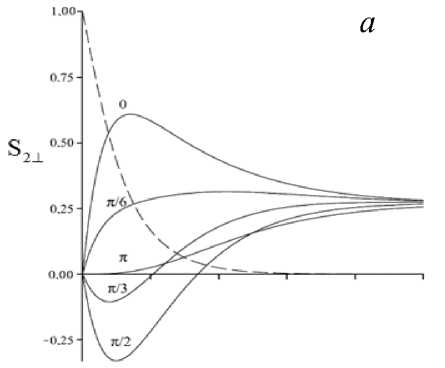
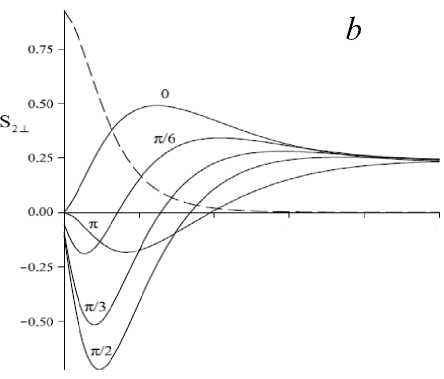
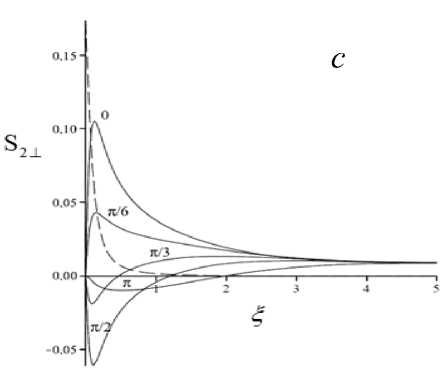
Рис. 3. Зависимость нормальной составляющей полного потока от толщины слоя для различных значений разности фаз при нормальном (а) и наклонном (т = 80 ° ) падении встречных волн р- и s-поляризации (b,c); пунктир - поток одиночной волны ных фаз Δϕba . Амплитуда таких осцилляций при увеличении угла падения терпит спад, более крутой для волн s-поляризации. Из сравнения рельефов S2⊥и Si2n⊥t видно, что роль ИП в процессе переноса излучения через слой достаточно велика. Форма поверхностей S2⊥ (τ, Δϕba ) фактически определяется рельефом зависимости S2in⊥t(τ,Δϕba).

Анализ приведенных зависимостей показывает, что встречные волны вносят существенно больший вклад в формирование полного интерференционного потока S ₂ ⁱⁿ _⊥ ^t по сравнению с однонаправленными волнами. С ростом толщины слоя увеличивается вклад интерференции встречных волн в общий ИП внутри поглощающего слоя и, соответственно, в потоки S ₁ ^r _, ^t ₃ . Таким образом, можно говорить о том, что ИП отраженных и прошедших волн в областях I и III образуются, главным образом, в результате туннельной интерференции встречных волн внутри слоя.

На рис. 3 для различных углов падения τ представлены зависимости нормальной составляющей полного потока на границе слоя S _{2 ⊥} ( ξ ) от относительной толщины ^ = d / d_s (здесь d _s – толщина скин-слоя). Видно, что поток одиночной волны (пунктирная линия) экспоненциально затухает с увеличением толщины слоя и на толщинах больших скин-слоя практически отсутствует. При наличии встречной волны наблюдаются характерные зависимости, которые при фиксированном угле падения зависят от фазовых соотношений на границах слоя. Наибольшие значения S _{2 ⊥} достигаются при нормальном падении, с увеличением угла падения эти значения будут уменьшаться (а при т ~ 80 ° будет проходить менее 20% падающего потока). На всех зависимостях прослеживается характерный максимумвеличины S _{2 ⊥} , который соответствует разности фаз § = 0 , при нормальном падении соответствующий толщине поглощающего слоя, чуть меньшей, чем d_s . На толщинах d ≥ 4 d_s интенсивность будет мало зависеть от разности фаз, и чем больше угол падения – тем это заметнее проявляется. Здесь же отметим, что поток на границе y = d всегда будет отличен от нуля S ₂ ^⊥ >0 (исключение составляет точка d = 0 ).

На рис. 4 представлены распределения нормальных составляющих полного S _{2 ⊥} и интерференционного потока S ₂ ⁱⁿ _⊥ ^t по толщине слоя d = 2 d для различных углов падения и начальных разностей фаз. Наибольшие значения обоих потоков достигаются при нормальном падении (как и на рис. 4) и соответствуют разностям фаз § = 0 (для полного потока, кривая 1) и 5 = п /2 (для интерференционного потока, кривая 4). Поскольку амплитуды падающих волн

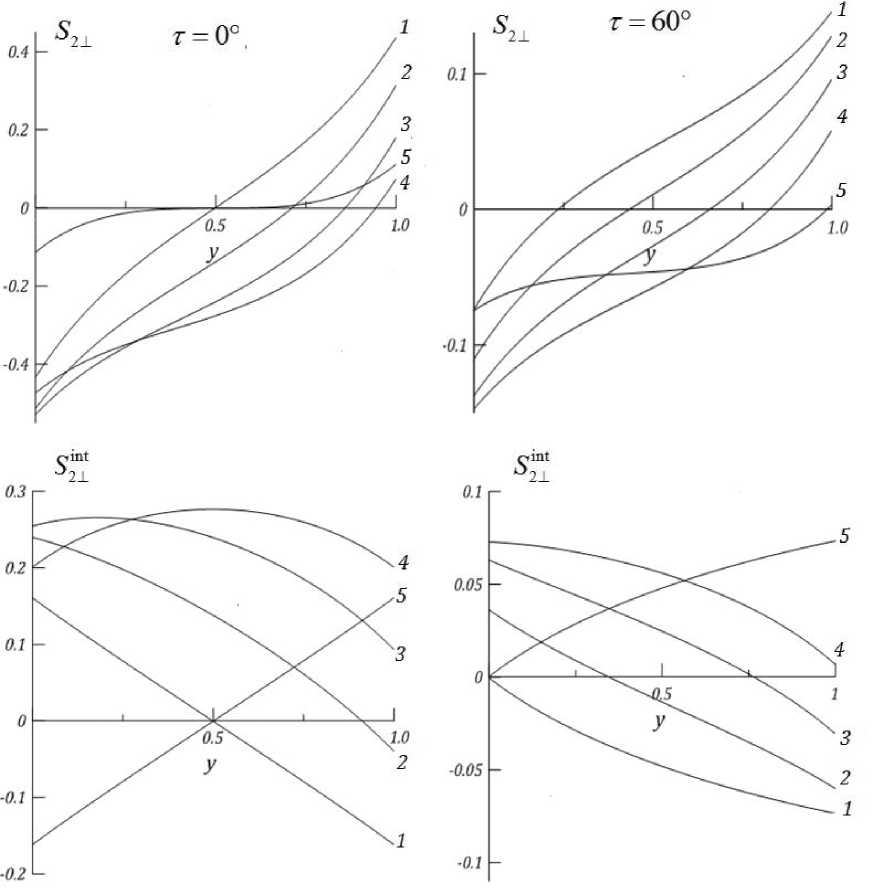
Рис. 4. Распределение по толщине слоя нормальной составляющей полного и интерференционного потоков при различных углах падения, разностях фаз бф_Ьа = 0, п /6, п / 3, п /2, п (кривые 1 - 5)

одинаковы, при нормальном падении и разности фаз б = 0, п имеет место симметричное распре-int деление потоков S2^ и о2± с нулевой интенсивностью в центре слоя. С увеличением разности фаз ноль интенсивности смещается в область больших толщин. Заметим, что интерференционный вклад на границе y = d будет увеличиваться с ростом б от 0 до п/2 (кривые 1-4), а величина S2± напротив - уменьшаться. Это означает, что вклады потоков одиночных волн на той же границе уменьшаются с увеличением δ.

Анализ показывает, что распределение по толщине слоя тангенциальной составляющей полного потока S2 не будет зависеть от фазовых соотношений и для различных углов падения представляет собой симметричное (относительно центра слоя) распределение. При этом макси- мальное значение величины S2D не превышает 0.15. При нормальном падении эта составляющая отсутствует. С увеличением угла падения абсолютные величины S2D возрастают вплоть до максимального значения, соответствующего углу падения т = 30°, а затем вновь происходит убыль величины S2D . При скользящем падении эта компонента также отсутствует.

На рис. 5 для пленки вольфрама толщиной d = 36 нм представлены зависимости от угла падения коэффициентов отражения R (кривые 1), прохождения T (кривые 2) и поглощения D для волн s- и p-поляризации (пунктирные и сплошные кривые). Для волн р-поляризации функция R (т ) вначале убывает, достигает минимального значения при т ₀ ~ 78 ° (аналог угла Брюстера), затем быстро возрастает и при

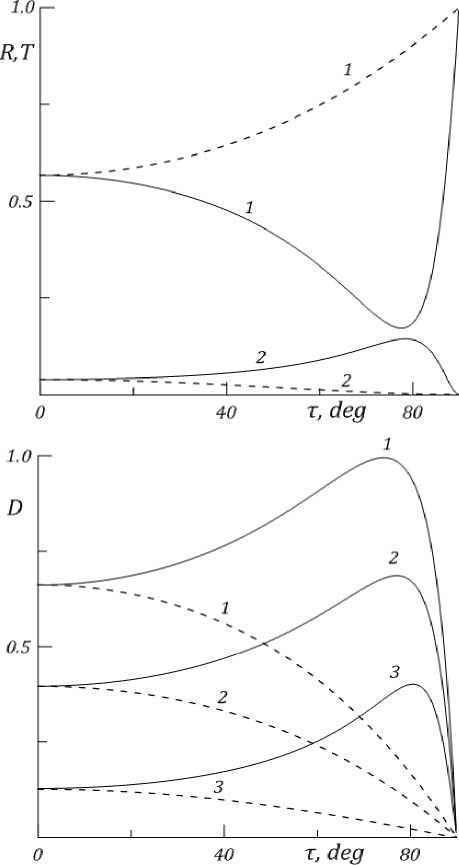
Рис. 5. Угловые зависимости для волн р- и s-поляризации (сплошная и пунктирная кривые) коэффициентов отражения R , прохождения T (кривые 1,2) и поглощения D (кривые 1-3 отвечают значениям § = 0, п /2, п ) для пленки вольфрама ( n = 3.4 5 - i 3.2 6 , d = 36 нм, X = 589 нм)

скользящем падении достигает максимального значения, практически равного единице. Функция T(т) плавно возрастает до точки То , где достигает максимального значения, а при скользящем падении обращается в нуль. Для волн s-поляризации наблюдается плавный рост величины коэффициента отражения и плавный спад коэффициента прохождения. Угловые зависимости коэффициента поглощения D (т) построены для значений начальной разности фаз § = 0, п /2, п (кривые 1-3). Для волн р-по-ляризации указанные зависимости имеют явно выраженный максимум в области углов, близких к То . При этом для нормального падения эффект поглощения будет выражен значительно слабее, чем при наклонном, а в области углов, близких к То в максимуме имеет место практически полное поглощение слоем энергии падающих волн. Так, величина коэффициента поглощения D в режиме двух встречных волн при наклонном падении и разности фаз § = 0 возрастает более чем на 50% (кривая 1). Величина коэффициента поглощения для волн s-поляризации с увеличением угла падения убывает, максимальный эффект отвечает нормальному падению. Таким образом, для эффективного нагрева металлической пленки целесообразно использовать наклонное падение волн р-поляризации. Отметим, что с увеличением толщины металлической пленки эффект поглощения будет уменьшаться, но преимущество наклонного падения перед нормальным так же для волн р-поляризации сохраняется.

Работа выполнена при поддержке Федерального агентства по науке и образованию в рамках федеральных целевых программ « Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 20072012 годы » и « Научные и научно-педагогические кадры инновационной России на 2009-2013 годы » .