Интерференционные логические элементы на основе фотонного кристалла с y-образным дефектом

Интерес к интерференционным логическим элементам на основе фотонных кристаллов (ФК) обусловлен их ожидаемыми достоинствами, такими как высокое быстродействие (что связано с отсутствием потерь на время отклика нелинейной среды, возникающих в устройствах традиционной микроэлектроники) и технологичность (для изготовления двумерных ФК-структур могут быть с успехом использованы хорошо отработанные планарные технологии микро- и наноэлектроники).

В [1] представлен достаточно содержательный обзор различных типов фотонно-кристаллических логических элементов. В данной статье рассматриваются исключительно двумерные фотонные кристаллы, представляющие собой кремниевые подложки (как вариант – активный слой подложки КНИ – кремний на изоляторе [2]) с набором цилиндрических отверстий (каверн), заполненных воздухом. Такой выбор обусловлен ориентацией на использование кремниевой технологии и нанолитографии (прямая запись фокусированным ионным пучком [3] или литографический процесс с использованием электронной или UV-литографии [4]). Таким образом, вне области интересов оказались фотонно-кристаллические логические элементы, работа которых основана на нелинейных эффектах (такие как в [5]). Кроме того, из рассмотрения исключены элементы на основе резонато- ров (например, из [1,6]), не самые удачные в плане простоты и быстродействия; а также многомодовые логические элементы (например, [7]), характеризующиеся невысокой дифракционной эффективностью.

Несомненный интерес представляет подход к расчету логических элементов с совместным использованием эффектов самоколлимации (для распространения излучения) и интерференции (производство собственно логических операций); соответствующие результаты приведены в [8, 9]. Отметим, однако, что небольшая (0,4 нм) разница в характеристических размерах элементов рассчитанного в [8] фотонного кристалла исключает использование для его изготовления доступной технологии.

Авторы настоящей статьи остановились на работе [10], как отправной точке своего исследования. Рассматриваемая в [10] фотонно-кристаллическая Y-образная структура характеризуется технологичностью. Интерференционный логический элемент (ИЛЭ), реализующий операцию “И”, на основе Y-образной структуры характеризуется эффективностью и быстродействием – в [10] приводится оценка быстродействия ИЛЭ около 1 Тбит/с.

Однако в своих расчетах авторы [10] принимали показатель преломления кремния на длине волны λ = 1,55 мкм равным 3,5, что верно при температуре в 143 ºС, либо для другой длины (λ = 1,31 мкм) при температуре в 20 ºС [11]. К тому же обсуждению в [10] подлежал лишь элемент, реализующий логиче- скую операцию «И». Тем более не исследована возможность каскадирования элементов.

1.    Выбор параметров фотонного кристалла

Проектирование топологии фотоннокристаллического элемента [1, 10] принято начинать с выбора параметров фотонно-кристаллической решетки, обеспечивающих его оптимальную работу. В данной работе рассматривалась двумерная фотоннокристаллическая структура с Y-образным дефектом (рис. 1), сформированная в кремнии травлением круглых отверстий. На пересечении трех линейных фотонно-кристаллических волноводов, сходящихся под углами 120° (в силу гексагональности решетки), расположено отверстие радиуса r 1 = 0,25 a ; остальные отверстия характеризуются r 2 =0,4 a , где a – период гексагональной кристаллической решетки [10].

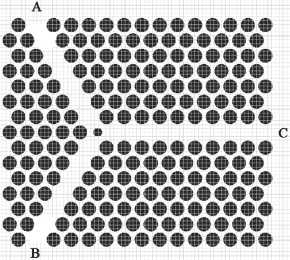
Рис. 1. Фотонный кристалл с Y-образным дефектом, характеризующийся периодом гексагональной кристаллической решетки a и отверстиями радиусов r 1 (отверстие в центре дефекта) и r 2 (отверстия, формирующие решетку). A и B – входы ФК ИЛЭ, C – выход

В силу упомянутого ранее несоответствия выбранной в [10] величины показателя преломления кремния ее реальному значению в данной работе решалась задача определения оптимальных параметров фотонно-кристаллической структуры (рис. 1) в кремнии. Для длины волны λ = 1,55 мкм и температуры 20°С показатель преломления среды принимался равным n = 3,4757 [8]. В качестве оптимальных параметров фотонно-кристаллической решетки понимались параметры решетки фотонно-кристаллического волновода с линейным горизонтальным дефектом (рис. 2), обеспечивающие распространение излучения в таком волноводе без потерь.

Учитывая, что большую площадь исследуемого Y-образного кристалла занимают три таких волновода и важность волноводной структуры самой по себе (связь между логическими интерференционными элементами и узлами ввода /вывода излучения), предложенный выбор критерия оптимальности представляется разумным.

Все вычислительные эксперименты проводились в пакете Ansys Lumerical R1 на компьютере с двумя процессорами Intel Xeon Silver 4214R 2,4 ГГц и оперативной памятью 2 Тб.

На первом этапе численно исследовалась линейная волноводная структура (рис. 2) со следующими параметрами: a = 367,2 нм, r 2 = 146,88 нм. Вычислительная область протяженностью 45 a в длину и 15 a в ширину заполнялась кремнием, в массиве которого располагались каверны радиуса r 2 . Линейный дефект (отсутствие горизонтального ряда каверн в кристалле) разделял область на две равные части. В качестве источника излучения выбирался магнитный диполь (магнитное поле поляризовано линейно вдоль воздушных каверн), расположенный на расстоянии 1,35 мкм от левого края волновода. Падающая волна задавалась в виде импульса шириной в 1 мкм (от λ 1 = 1,05 до λ 2 = 2,05 мкм). На расстоянии 2,95 мкм от левого края (между восьмым и девятым кавернами) помещался первый монитор (вертикальный отрезок шириной 2 мкм; энергия проходящей через него волны фиксируется, ее значение принимается результатом эксперимента). Предполагалось, что на упомянутом расстоянии режим распространения является устоявшимся для всех длин волн диапазона λ 1 – λ 2 . Второй монитор находится на расстоянии 3,35 мкм от правого края структуры (между 34-й и 35-й кавернами) и необходим для контроля выходного излучения.

Рис. 2. Тестовая структура

Сравнение показаний двух мониторов, представленных на рис. 3, позволяет делать выводы о возможности волноводного распространения в исследуемой структуре.

Следуя методу расчета фотонно-кристаллических элементов, изложенному в [12], в первом эксперименте (в отличие от следующих) сознательно пренебрежем дисперсией показателя преломления кремния.

Wavelength (microns)

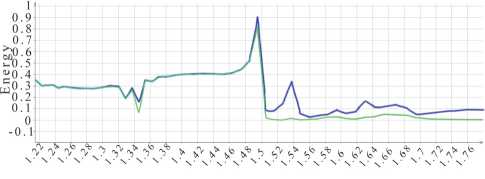
Рис. 3. Зависимость энергии излучения, прошедшего через мониторы, от длины волны. Синяя линия соответствует первому (входному монитору), зеленая – второму (выходному)

На рис. 3 видно, что фотонно-кристаллическая структура с выбранными параметрами не обеспечивает каналируемого распространения излучения (возникают потери энергии при распространении излучения по волноводу) для рабочей длины волны λ = 1,55 мкм. Однако заметны два относительно ровных участка: от λ = 1,39 до λ = 1,45 мкм и от λ = 1,24 до λ = 1,31 мкм, для которых характерно распространение практически без потерь.

Пересчет параметров фотонно-кристаллической структуры производился в ходе одной итерации (в силу отсутствия проводящих материалов) итерационной процедуры [12]. В результате пересчета в качестве оптимальных были выбраны следующие параметры фотонно-кристаллической структуры: a =459 нм, r 2 = 183,9 нм, r 1 =114,75 нм. Выбранные параметры использовались для проектирования ФК ИЛЭ.

2.    Реализация операций «И», «ИЛИ», «ИСКЛЮЧАЮЩЕЕ ИЛИ» и «НЕ»

Переходя к исследованию фотонного кристалла с Y-образным дефектом (рис. 1), во второй серии экспериментов (рис. 4, табл. 1) ограничимся рассмотрением его квадратного фрагмента со стороной в 15 периодов. Источники излучения будем располагать в левом верхнем ( A ) и левом нижнем ( B ) рукавах на расстоянии 2,9 мкм от центра кристалла (центр малого отверстия).

Фаза излучения у обоих источников полагалась одинаковой. Монитор для регистрации излучения в правом рукаве ( C ) располагается на расстоянии 3,25 мкм от того же центра. Все остальные параметры (характеристики источников, сеточной области, мониторов) заимствуются из предыдущего эксперимента.

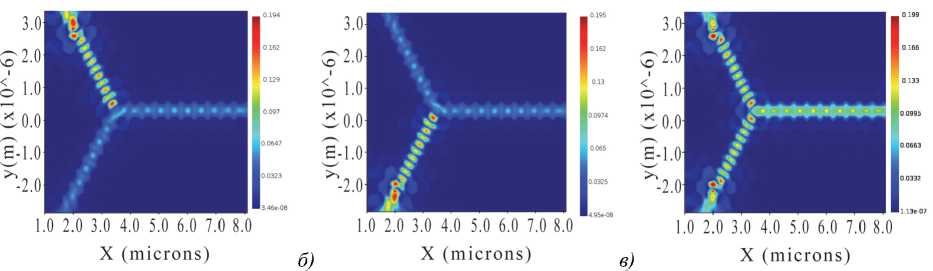
Рис. 4. Результаты численного моделирования фотонного кристалла с Y-образным дефектом (распределение модуля комплексной амплитуды) во второй серии экспериментов: (a) включен источник на входе A, (б) включен источник на входе B, (в) включены оба источника

После нормировки интенсивности на выходе C к интенсивности на входе волновода в первом эксперименте (значение последней принималось за единицу) были получены результаты, представленные в первых трех колонках табл. 1. При этом вклад отраженных волн (они достигнут входов A и B ) не учитывается.

Табл. 1. Результаты второй серии экспериментов

Ia	Ib	Ic	«И»	«ИЛИ»
0	0	0	0	0
1	0	0,417	0	1
0	1	0,417	0	1
1	1	0,83	1	1

В третьей колонке табл. 1 представлены нормированные значения интенсивностей ( I C – на выходе C ), в последних двух – результаты выполнения логических операций «И» и «ИЛИ» [13].

Содержимое первых двух колонок можно интерпретировать и как нормированные интенсивности (IA – на входе A, IB – на входе В), и как операнды логических операций (IA – первый операнд, IB – второй). Устанавливая пороговое значение различения логических сигналов «0» и «1» между 0,42 и 0,82 (например, как 0,5), можно интерпретировать представленные в третьей колонке табл. 1 данные как результаты логической операции «И» (четвер- тая колонка табл. 1); принимая пороговое значение меньше 0,41, можно говорить о результатах логической операции «ИЛИ» (пятая колонка табл. 1).

Вопросы физической реализации такой пороговой обработки оставим за рамками настоящего рассмотрения. Сопоставляя рис. 4 и табл. 1, отметим, что третья строчка таблицы соответствует рис. 4 a , четвертая и пятая – рис. 4 б и рис. 4 в соответственно. Эксперимент, соответствующий второй строчке, не проводился за очевидностью результата.

В третьей серии экспериментов (рис. 5, табл. 2) предполагалось, что разница фаз излучения источников составляла π, значения остальных параметров полагались прежними.

Тогда, установив пороговое значение меньше 0,41, можем интерпретировать данные из третьей колонки табл. 2 как результаты логической операции «ИСКЛЮЧАЮЩЕЕ ИЛИ» (четвертая колонка).

Отдельное внимание обратим на два эксперимента третьей серии, связанные с работой источника на входе A и соответствующие: рис. 5а (третья строчка табл. 2) и рис. 5в (пятая строчка табл. 2). Принимая упомянутый вход за источник опорного (всегда включенного и не являющегося операндом логической операции) сигнала и интерпретируя вход B как источник операнда для унарной операции, наблюдаем в пятом столбце табл. 2 результат операции «НЕ» при

3.    Каскадирование ФК ИЛЭ том же пороговом значении.

Табл. 2. Результаты третьей серии экспериментов

Ia	Ib	Ic	«ИСКЛЮЧАЮЩЕЕ ИЛИ»	«НЕ»
0	0	0	0	–
1	0	0,414	1	1
0	1	0,413	1	–
1	1	0	0	0

Дальнейшим шагом в развитии фотонных цифровых вычислительных устройств на основе ИЛЭ является объединение ИЛЭ в одну схему [1], включающее в том числе последовательное соединение ИЛЭ или, иначе, их каскадирование . Последовательное производство логических операций накладывает существенное ограничение на фазу выходного сигнала ИЛЭ – фаза должна быть детерминирована.

a)

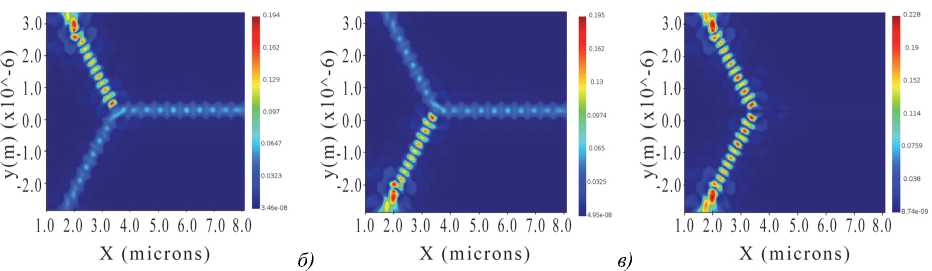
Рис. 5. Результаты численного моделирования фотонного кристалла с Y-образным дефектом (распределение модуля комплексной амплитуды) в третьей серии экспериментов:(a) включен источник на входе A, (б) включен источник на входе B, (в) включены оба источника в противофазе

Допустим, решено применить операцию «НЕ» к результату операции «ИСКЛЮЧАЮЩЕЕ ИЛИ», реализовав каждую из операций на основе фотонного кристалла, изображенного на рис. 1. Расположив элемент, реализующий «НЕ», после элемента, производящего «ИСКЛЮЧАЮЩЕЕ ИЛИ», необходимо знать фазу волны на выходе С первого элемента. Лишь в этом случае удастся организовать отрицательную интерференцию с такой волной, реализовав тем самым операцию «НЕ». Однако в предыдущем рассмотрении отмечалась необходимость подачи противофазных волн на входы элемента, реализующего «ИСКЛЮЧАЮЩЕЕ ИЛИ». В таком случае фаза вышедшей из данного элемента волны, соответствующего результату «истина», оказывается неопределенной: фазы двух выходящих из элемента волн (при разных входных сигналах 0 1 или 1 0), означающих «истину», отличаются на π. Организация отрицательной интерференции таких волн при реализации последующей операции «НЕ» становится невозможной.

Указанное обстоятельство (проблема неопределенности фазы) не исключает использование элемента, производящего «ИСКЛЮЧАЮЩЕЕ ИЛИ», в каскаде (например, последним его элементом), однако ограничивает использование такого элемента при каскадировании. Отметим, что это проблема не только реализации операции «ИСКЛЮЧАЮЩЕЕ ИЛИ», но и других операций – «ИЛИ», «ИЛИ-НЕ» и т.д. Проблема неопределенности фазы заключается в зависимости фазы выходного сигнала, соответствующего значению 1, от значений операндов у ИЛЭ типа «ИЛИ», «ИЛИ-НЕ», «ИСКЛЮЧАЮЩЕЕ ИЛИ» и др. Различное значение фазы выходного сигнала (напри- мер, у ИЛЭ «ИЛИ» при различном выборе операндов - (1,0) или (1,1)) делает невозможным каскадирование таких элементов, так как подача сигналов, соответствующих 1, но с различной фазой, на вход ЛЭ следующего каскада очевидно приведет к различным результатам.

Для решения этой задачи в данной работе предлагается использовать тот факт, что логические операции «И» и «НЕ» образуют минимальный полный базис [13] и, следовательно, любая другая логическая операция может быть представлена в виде их комбинации.

На рис. 6 представлен один из вариантов построения логического элемента «ИЛИ-НЕ» на основе комбинации операций «И» и «НЕ», приведенный в [13].

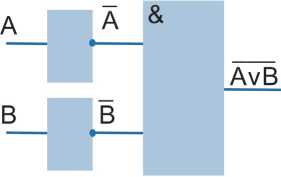
Рис. 6. Логический элемент «ИЛИ-НЕ» на основе комбинации операций «И» и «НЕ»

Отметим при этом, что ИЛЭ, реализующие операции «И» и «НЕ», не обладают проблемой неопределенности фазы. Соответственно, возможно построение ИЛЭ, реализующего любую логическую функцию и не обладающего проблемой неопределенности фазы, в виде комбинации ИЛЭ, реализующих операции «И» и «НЕ».

В ходе четвертой серии численных экспериментов в данной работе исследовался ИЛЭ, реализующий опера- цию «ИЛИ-НЕ», на основе комбинации ИЛЭ «И» и «НЕ», соединенных, как схематично показано на рис . 6.

На рис. 7 предложена реализация такого решения, где входы A и B есть входы первого элемента, реализующего «НЕ»; C и D – входы второго элемента, также связанного с производством «НЕ» (параллельно с первым); выход E является выходом третьего элемента – «И» и одновременно составного элемента – «ИЛИ-НЕ».

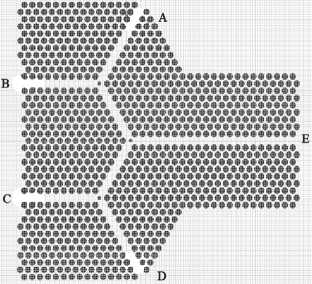
Рис. 7. Фотонный кристалл с тремя Y-образными дефектами, реализующий логическую операцию «ИЛИ-НЕ». B и C – входы для сигналов-операндов, A и D – входы для опорных сигналов, E – выход для сигнала-результата операции

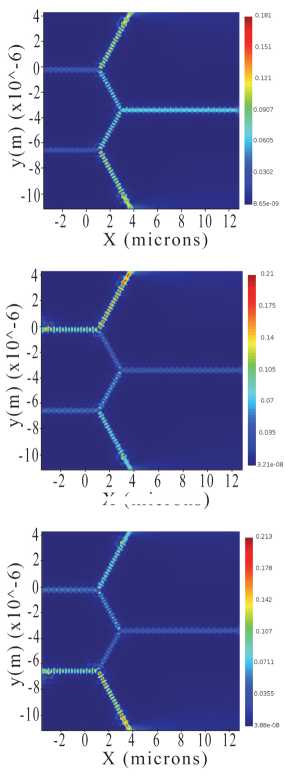
На рис. 8 и в табл. 3 представлены результаты четвертой серии численных экспериментов.

Табл. 3. Результаты четвертой серии экспериментов

Ib	Ic	Ie	«ИЛИ-НЕ»
0	0	0,35	1
1	0	0,07	0
0	1	0,06	0
1	1	0,0009	0

Установив пороговое значение меньше 0,34, можем интерпретировать данные из третьей колонки табл. 4 как результаты логической операции «ИЛИНЕ» (четвертая колонка). При этом сигнал, соответствующий «истине» на выходе E , имеет всегда одинаковую фазу.

Отметим, что результаты численного моделирования ИЛЭ (рис. 7) демонстрируют принципиальную возможность каскадирования ИЛЭ (на примере элементов «И» и «НЕ»).

Также отметим, что операции «НЕ» и «И» составляют минимальный полный базис, посредством которого можно представить любые другие логические операции. Следовательно, при каскадировании элементов, производящих «НЕ» и «И», теоретически можно построить составной элемент, реализующий любую логическую операцию.

Заключение

Продемонстрирована возможность построения интерференционных логических элементов, реализующих полный базис логических операций, на основе фотонно-кристаллической структуры с гексагональной решеткой и Y-образным дефектом. На примере составного элемента, реализующего операцию «ИЛИ-

НЕ», показана принципиальная возможность каскадирования ИЛЭ (в данном случае «И» и «НЕ») в одну схему. При этом показано увеличение отношения интенсивностей сигналов, соответствующих «1» и «0», по сравнению с одиночным элементом. Показана принципиальная возможность решения проблемы неопределенности фазы при построении ИЛЭ, на основе использования разложения логических операций по минимальному полному базису «НЕ» и «И».

а)

б)

в)

X (microns)

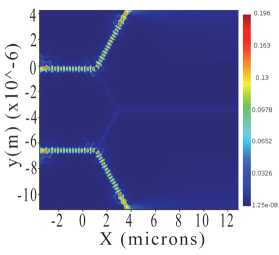
Рис. 8. Результаты численного моделирования структуры, приведенной на рис. 7, в четвертой серии экспериментов:

(a) источники на входе B и С выключены; (б) включен источник на входе B, на C выключен; (в) включен источник на входе С, на B выключен; (г) включены источники на B и C. Источники на входах A и D включены всегда, как источники опорных сигналов

При этом необходимо учесть, что в случае использования линейных ФК интенсивность выходных сигналов ИЛЭ будет неизбежно падать по сравнению со входными сигналами. Для выравнивания значений интенсивности разных каскадов (последующих и предыдущих) целесообразно рассмотреть использование уменьшения выходных интенсивностей предыдущих каскадов с помощью ФК делителей пучка [14] c соответствующим числом выходов. Такая необходимость может возникнуть, например, при необходимости совершения логической операции над сигналами разных участков схемы.

Для обеспечения необходимых значений фаз на входах ИЛЭ при каскадировании предполагается использовать линии задержки на основе волноводов заданной длины.

Работа выполнена в рамках научной программы Национального центра физики и математики (НЦФМ). Раздел “Заключение” написан при частичной поддержке Государственного задания ФНИЦ «Кристаллография и фотоника» РАН.