Интерферометрические наблюдения мерцаний дискретного радиоисточника Лебедь-А на Иркутском радаре некогерентного рассеяния

значительную роль, — это спутниковые коммуникации и радиоастрономия. В настоящее время разработан ряд моделей, которые описывают и в некоторой мере предсказывают поведение ионосферных мерцаний в планетарном масштабе [Priyadarshi, 2015]. Исследование свойств мерцаний в некоторых случаях позволяет определять характеристики ионосферных неоднородностей [Безродный и др., 2010].

Иркутский радар некогерентного рассеяния (ИРНР), работающий в пассивном режиме, также способен наблюдать мерцания радиоволн от дискретных космических радиоисточников (ДКР) в ионосфере [Vasilyev et al., 2013]. Особенности регистрирующей системы ИРНР позволяют выполнять интерферометрические [Лебедев и др., 2013] наблюдения ионосферы и объектов на околоземной орбите. Эти особенности можно задействовать также для наблюдения за ДКР и их характеристиками.

ИНТЕРФЕРОМЕТРИЯ ИОНОСФЕРНЫХ МЕРЦАНИЙ

Эффекты распространения метровых радиоволн в ионосфере, как правило, негативны для работы радиотелескопов-интерферометров. Рефракционные эффекты, возникающие при распространении сигнала в неоднородной среде, искажают истинное положение источника излучения и его размер [Spoelstra, Kelder, 1984]. Вариации характеристик ионосферы имеют различный характер. Существуют сезонные и суточные вариации электронной концентрации, ее эволюция по высоте, а также волновые явления (перемещающиеся ионосферные возмущения), имеющие характерные периоды порядка нескольких часов и размеры от десятков до тысяч километров. Эти относительно плавные вариации характеристик ионосферы играют существенную роль для радиоинтерферометров, обладающих базой порядка нескольких километров и более. Они могут быть учтены при помощи либо существующих моделей ионосферы [Sukumar, 1987], либо вспомогательных наблюдений ионосферы. Ионосферные неоднородности с масштабом порядка одного километра в связи с тем, что их размер приближается к размеру зоны Френеля для метровых волн на высотах ионосферы, будут приводить к дифракционным эффектам, которые выражаются в мерцаниях радиосигнала ДКР. Они регистрируются интерферометром при наблюдении ДКР и могут иметь различный характер: в зависимости от соотношения размеров неоднородностей и базы интерферометра можно различать амплитудные и фазовые мерцания радиосигнала на выходе коррелятора. Если размер базы интерферометра (расстояние между антеннами) будет существенно меньше размера неоднородности, вариации радиосигнала в различных антеннах интерферометра будут синхронными и на выходе коррелятора будут наблюдаться вариации соотношения сигнал/шум, что является проявлением так называемых амплитудных мерцаний. Относительная фаза сигналов при этом будет изменяться медленно в соответствии с перемещением ДКР по небесной сфере вследствие суточного вращения Земли. При увеличении базы интерферометра до размеров, сопоставимых с размерами ионосферных неоднородностей или превышающих их, фазовые задержки сигналов в антеннах интерферометра, обусловленные прохождением радиоволны через участки с различной электронной концентрацией, начнут различаться. Это приведет к сложению в корреляторе сигналов с разными задержками, и вариация сигнала на выходе коррелято-

M.V. Globa, R.V. Vasilyev, D.S. Kushnaryov, A.V. Medvedev ра уже будет обусловлена как вариацией соотношения сигнал/шум, так и усилением или ослаблением выходного сигнала вследствие синфазного или противофазного суммирования, что является проявлением фазовых мерцаний. В этом случае на плавное изменение фазы сигнала от ДКР за счет вращения Земли будут накладываться быстрые вариации фазы, которые в конечном итоге будут влиять на наблюдаемое положение и размер ДКР. Более подробно этот вопрос был исследован в работе [Spoelstra, Yang Yi-Pei, 1995], в которой показана зависимость ослабления амплитудных мерцаний и увеличения фазовых мерцаний от роста базы интерферометра.

ИРКУТСКИЙ РАДАР НЕКОГЕРЕНТНОГО РАССЕЯНИЯ КАК РАДИОИНТЕРФЕРОМЕТР

Антенная система ИРНР, предназначенная для осуществления частотного сканирования участка небесной сферы размером 20°×30°, состоит из двух независимых смежных приемо-передающих секториальных рупоров (полурупоров). Линейные размеры антенной системы составляют 250×20×12 м, общий раскрыв полурупоров (250×12 м) имеет площадь 3000 м2. Щелевые излучатели питающих волноводов, лежащих в основании каждого полурупора, формируют линейную антенную решетку, обеспечивающую ширину 0.5° диаграммы направленности (ДН) в плоскости сканирования, стенки полурупоров обеспечивают ширину ДН 20° в плоскости, перпендикулярной плоскости сканирования. Эффективная площадь апертуры антенны составляет ~1000 м2. Частотный диапазон радара 154–162 МГц, что соответствует длине волны около двух метров. Форма ДН радара, а также точные коэффициенты уравнения сканирования могут быть получены при наблюдении ДКР. Совместное наблюдение ДКР двумя полурупорами позволяет также определить характеристики интерферометра, который они образуют. Наклон характеристики, связывающей перемещение ДКР по небесной сфере и разность фаз сигнала в полурупорах, составляет 16 электрических градусов на один градус небесной сферы [Лебедев и др., 2006]. Расстояние между фазовыми центрами антенн при этом порядка 5 м. База интерферометра на основе антенной системы ИРНР мала, и поэтому ширина основного лепестка интерферометра составляет порядка 11°. Ширина ДН обоих полурупоров в плоскости, в которой лежат фазовые центры, — около 20°. Таким образом, главный лепесток интерферометра полностью помещается в ДН антенной системы.

Регистрация сигналов в полурупорах ведется при помощи специализированной системы, позволяющей сохранять принимаемый в каждом рупоре сигнал в виде ряда комплексных чисел в устройствах долговременного хранения. Система состоит из аналоговой усилительно-гетеродинной части, усиливающей принятый сигнал и понижающей частоту до диапазона, приемлемого для работы цифровых регистрирующих устройств; шестнадцатиразрядного АЦП, регистрирующего сигнал на выходе аналоговой части с частотой оцифровки 1 МГц, и сигналь- ного процессора, раскладывающего результат работы АЦП на комплексные составляющие. Регистрация сигналов системой ведется интервалами длительностью 8 мс (временные реализации) с периодом около 40 мс. Управление работой системы и окончательное представление полученных данных осуществляется посредством управляющей ЭВМ. Полученные на рабочей машине результаты наблюдений передаются в локальную вычислительную сеть ИРНР и сохраняются на жестких дисках серверной ЭВМ для дальнейшей обработки и хранения.

Запись сигналов в комплексном виде удобна с точки зрения корреляционной обработки. Отсутствует необходимость создания дополнительного устройства (коррелятора), входящего в состав измерительной системы, есть возможность варьировать время интегрирования при последующей обработке и т. п. Для корреляционного анализа данных мы использовали коэффициент взаимной корреляции сигналов в рупорах антенной системы

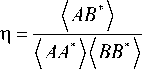
где A и B — сигналы независимых рупоров (антенн интерферометра), звездочка означает операцию комплексного сопряжения, а угловые скобки — усреднение по времени. Нетрудно показать, что аргумент полученной величины отражает положение источника относительно фазовых центров, а модуль — соотношение сигнал/шум (см. приложение 1). Традиционно коэффициент когерентности рассматривается как некая статистическая характеристика, и формально для него можно получить не только среднее значение, но и моменты более высоких порядков, которые будут отражать изменение формы наблюдаемого ДКР. Однако есть вероятность того, что из-за содержания шумовой составляющей в сигнале статистические моменты будут испытывать вариации, не относящиеся к вариациям размера и положения ДКР за счет ионосферы. Это обстоятельство привело нас к решению рассматривать не усредненные характеристики, а статистические распределения (гистограммы), и на основе анализа формы этих распределений делать выводы о наблюдаемом положении источника на небесной сфере и его размере.

ДВУМЕРНАЯ ГИСТОГРАММА РАДИОИСТОЧНИКА ЛЕБЕДЬ-А И ЕЕ ХАРАКТЕРИСТИКИ

Радиогалактика Лебедь-А является одним из самых ярких радиоисточников на северной небесной полусфере. Он ежедневно проходит через сектор обзора ИРНР, поэтому с ним наиболее удобно работать при анализе данных. Активные наблюдения на ИРНР выполняются с использованием некоторой фиксированной частоты, что соответствует наклону ДН в конкретном направлении в секторе обзора. Во время активных наблюдений можно выбрать момент времени, когда через ДН проходит ДКР Лебедь-А, и использовать полученные в этот момент данные активных наблюдений радара для исследований

ДКР. Данные представляют собой временные реализации принятого сигнала, содержащие как рассеянный в ионосфере зондирующий сигнал, так и фоновое космическое радиоизлучение. Поэтому необходимо отбрасывать начальную часть реализации, на которой зондирующий сигнал имеет значимую величину, и анализировать только конечную часть, начиная с дальности ~600 км. Изменение частоты принимаемого радиоизлучения означает перемещение источника вдоль плоскости Север–Юг, а изменение разности фаз между двумя полурупорами — перемещение вдоль плоскости Запад–Восток. Для определения координат ДКР в этих направлениях необходимо анализировать частотный спектр принятого радиосигнала и аргумент коэффициента корреляции радиосигналов в полурупорах (1). При обработке данных для каждой реализации проводилось преобразование Фурье, а затем вычисление аргумента коэффициента корреляции между полурупорами для каждой частотной компоненты:

arg( η i )=arg( a i b i ), (2) где i — номер частотной компоненты; a , b — спектральные отсчеты сигналов полурупоров. Эти значения накапливались в двумерной гистограмме на протяжении периода 18 с. За этот же период проводилось накопление значений коэффициента корреляции:

Н i = ∑ k

a ik b i ^∗ k

a ik a i ^∗ k b ik b i ^∗ k

где k — временные отсчеты, i — отсчеты по частоте.

Каждое значение накопленной двумерной гистограммы умножалось на модуль соответствующего коэффициента корреляции для нормировки. Таким образом, формировалось распределение мощности сигнала ДКР по частоте и фазе. Конечно, это распределение можно было бы считать изображением радиоисточника, однако такое изображение неполноценно, поскольку распределение мощности по одной из координат (фазе) получено на основании интерферометра с одним плечом (одной базой) и фактически представляет поведение некого эффективного центра тяжести полного изображения по этой координате. Распределение мощности по другой координате (частоте) является сверткой изображения с ДН. Из соображений удобства и краткости эту двумерную гистограмму распределения мощности ДКР по частоте и фазе мы будем называть изображением радиоисточника. На рис. 1 представлены три изображения, полученные в последовательные моменты времени.

Источник проходит через ДН в течение 10–15 мин, для анализа перемещения ДКР по ДН радара вычислялись положение максимума и среднее значение яркости для каждого изображения (рис. 2, а , б ). В отсутствие ДКР положение максимума меняется случайным образом, в то время как среднее значение остается сравнительно постоянным. При появлении источника среднее значение меняется медленно и не вполне корректно отображает перемещение источника по сектору обзора. Следовательно, можно сде-

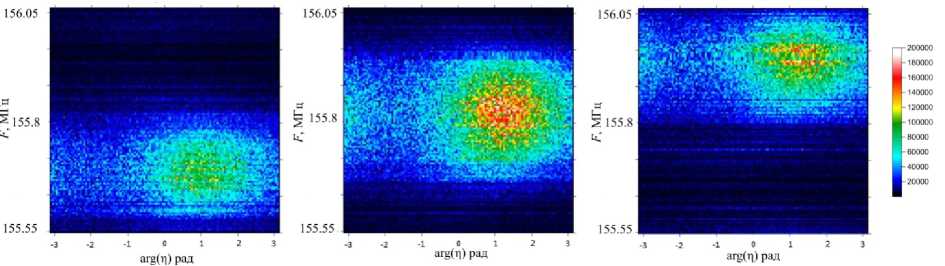
Рис. 1. Изображения радиоисточника, построенные за время накопления 18 с

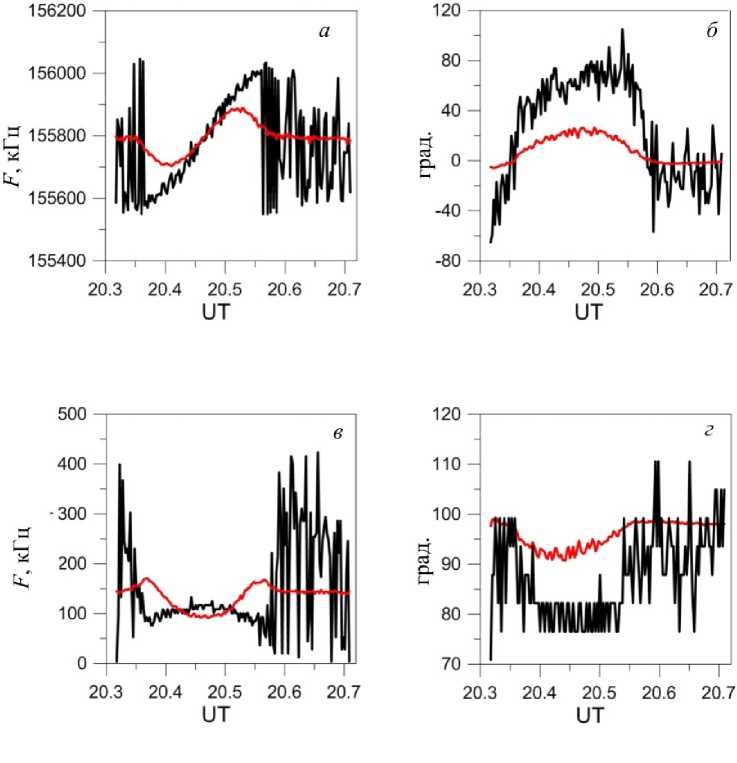
Рис. 2. Изменение положения максимального значения (черная линия) и среднего значения распределения (серая линия) для частоты ( а ) и фазы ( б ); изменение среднеквадратического отклонения (серая линия) и ширины гистограммы (черная линия) для частоты ( в ) и фазы ( г ) 28 июня 2013 г.

лать вывод о том, что для наблюдения за положением источника лучше следить за изменением максимального значения распределения.

Для анализа ширины изображения ДКР вычислялись среднеквадратичное отклонение и ширина гистограммы на уровне половинной амплитуды (рис. 2, в , г ). Видно, что для частоты (рис. 2, в ) среднеквадратичное отклонение также медленно изменяется при появлении источника и не точно отображает изменение ширины изображения.

ПОВЕДЕНИЕ ХАРАКТЕРИСТИК ИЗОБРАЖЕНИЙ ДКР ЛЕБЕДЬ-А В УСЛОВИЯХ МЕРЦАНИЙ

И СМЕНЫ СЕЗОНОВ

При работе ИРНР в штатном режиме регистрация радиосигналов ведется непрерывно на протяжении нескольких суток. Сканирование ДН осуществляется не в полной мере. Как правило, выбираются два фиксированных направления, которые циклически

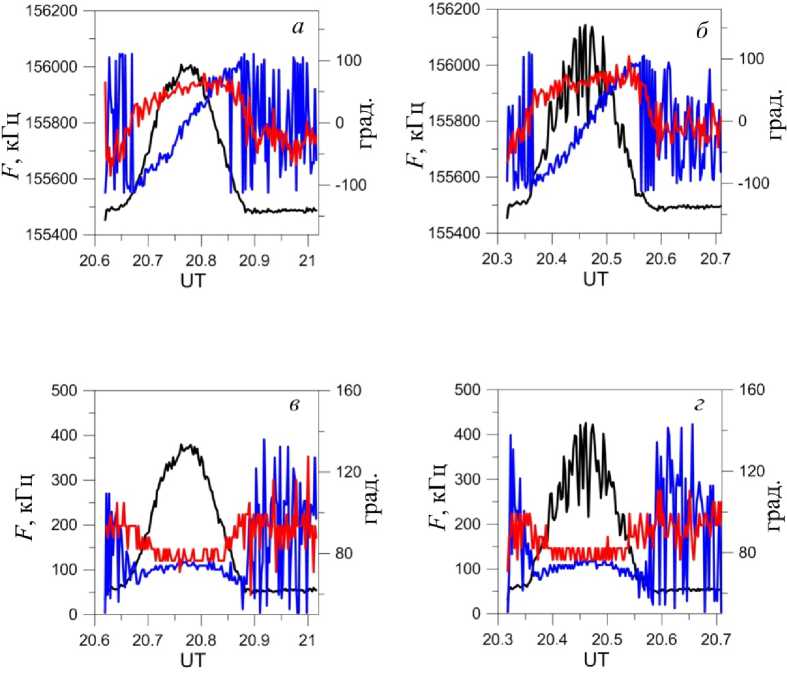
Рис. 3. Изменение мощности (тонкая черная линия) и основных характеристик изображения ДКР для широкополосного канала (500 кГц). На панелях а , б толстая черная кривая — изменение положения максимума распределения по частоте, толстая серая — изменение положения максимума по фазе; на панелях в , г толстая черная кривая — изменение ширины на полувысоте по частоте, тонкая серая — по фазе. 23 июня ( а , в ) и 28 июня ( б , г ) 2013 г.

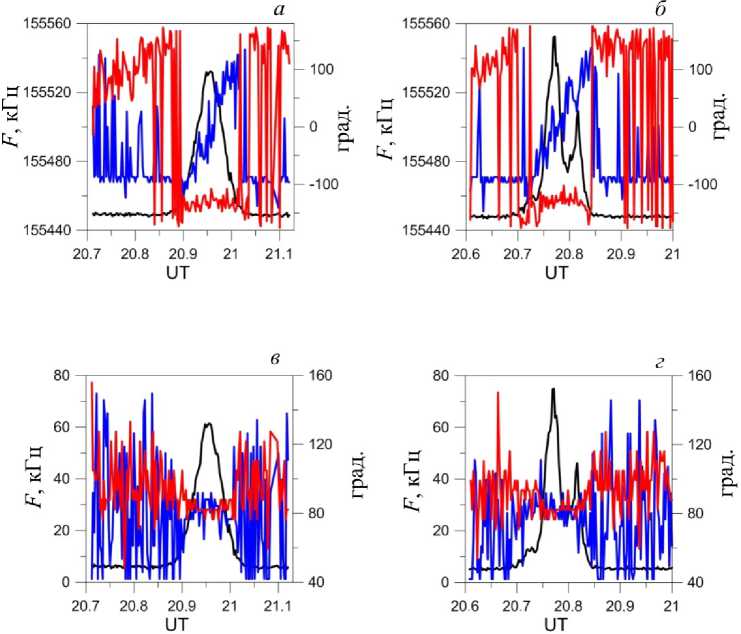
Рис. 4. То же, что на рис. 3, для узкополосного канала (100 кГц) для 23 июня ( а , в ) и 26 июня ( б , г ) 2013 г.

просматриваются радаром. ДКР, перемещающиеся по сектору обзора, проходят через ДН, ориентированную на определенное направление, и раз в сутки для выбранного ДКР существует относительно короткий интервал наблюдения. Поскольку минимальная ширина ДН составляет порядка половины градуса, ДКР проходит через ДН за время порядка 15 мин. Этого времени достаточно, чтобы зафиксировать возникающие ионосферные мерцания ДКР в устройстве хранения.

На рис. 3 и 4 показаны изменение вычисляемых характеристик изображений и изменение мощности принимаемого сигнала по мере перемещения ДКР для широкополосного (500 кГц) и узкополосного (100 кГц) каналов соответственно. Изображения построены для относительно спокойного дня без мерцаний (23 июня 2013 г. — рис. 3, а , в ; 4, а , в ) и для двух дней, когда наблюдались заметные мерцания (28 июня 2013 г. — рис. 3, б , г ; 26 июня 2013 г. – рис. 4, б , г ). Очевидно отсутствие существенных различий в поведении вычисляемых параметров при разных условиях. Отсюда следует, что мерцания не влияют на размер и положение изображения ДКР. Это связано с тем, что расстояние между антеннами радара составляет 5 м, что существенно меньше первой зоны Френеля для ионосферных неоднородностей, наблюдаемых в этом случае, поэтому возможно только наблюдение синхронных амплитудных мерцаний в полурупорах.

Поскольку ИРНР в штатном режиме работает около 50–100 дней в году, несмотря на кратковременность суточного периода наблюдений, существует достаточно обширный материал для обработки. В таблице представлены средние значения некоторых вычисляемых характеристик за летний и зимний периоды 2013 г. Можно отметить, что существенного различия в этих характеристиках для различных сезонов не наблюдается.

Сезон Лето Зима Средний индекс мерцаний 0.031 0.034 Средняя ширина изображения ДКР по частоте 46.642 45.875 Средняя ширина изображения ДКР по фазе 47 47.375 Среднее отклонение положения максимума от прямолинейной траектории (по частоте) 14.328 18.184 не влияют на параметры изображения ДКР, в особенности на поведение фазы, что находится в соответствии с проведенными ранее исследованиями [Spoelstra, Yang Yi-Pei, 1995]. Поскольку расстояние между антеннами радара существенно меньше размеров неоднородностей, фазовые мерцания можно наблюдать только для сверхмелкомасштабных неоднородностей (метры и десятки метров). Чтобы наблюдать фазовые мерцания для крупномасштабных неоднородностей, необходимо проводить синхронные наблюдения с отдаленными регистраторами для увеличения базы интерферометра. Показано, что в различные сезоны не наблюдается существенных различий в значениях статистических параметров. Это может быть связано с тем, что сигналы регистрировались с минимально возможным интегрированием, поэтому дополнительно было проведено исследование влияния времени интегрирования на размер изображения источника. На рис. 5 показано изменение ширины статистического распределения аргумента коэффициента корреляции в зависимости от количества реализаций, участвующих в вычислении коэффициента корреляции. Видно, что с увеличением числа реализаций ширина значительно уменьшается, а затем выходит на практически постоянное значение. Выход ширины на константу происходит после 100 реализаций, что соответствует времени интегрирования 4 с. Его рекомендуется использовать при дальнейшем анализе данных интерферометрических исследований сигнала от радиоисточника Лебедь-А.

Статистические характеристики изображений ДКР, определенные по методике, описанной в данной работе, в дальнейшем необходимо связать с характерными размерами ионосферных неоднородностей, а также их интенсивностью. Для этого требуется выполнить моделирование прохождения излучения ДКР через неоднородную ионосферу, используя, например, метод фазового экрана. Поскольку в работе показано, что наиболее вероятное значение статистического распределения и его ширина не зависят от мерцаний радиосигнала, в работах, связанных с моделированием, необходимо обратить внимание на саму форму распределения (асимметрия, гранулярность) и ее вариации в зависимости от характеристик фазового экрана.

Работа выполнена при поддержке гранта РФФИ 13-05-03946 А.

ЗАКЛЮЧЕНИЕ

В данной статье был предложен метод анализа изображения ДКР Лебедь-А, которое получено на основе статистических распределений интерференционных характеристик принимаемого сигнала. По сравнению с анализом статистических моментов анализ формы статистических распределений более качественно отражает характеристики ДКР, такие как положение и угловой размер. С использованием предложенного метода был проведен анализ ионосферных мерцаний ДКР Лебедь-А. Показано, что наблюдаемые на ИРНР ионосферные мерцания ДКР

Рис. 5. Зависимость ширины гистограммы от количества просуммированных реализаций 22 июня 2013 г.

ПРИЛОЖЕНИЕ

Пусть в некоторую точку приходит плоская волна под углом θ (рис. 1п). Рассмотрим сигналы на выходе двух независимых антенн, фазовые центры которых расположены на расстоянии d :

В числителе выражения (8) все члены суммы, кроме первого, при усреднении также обратятся в нуль из-за независимости фаз. Выражение для коэффициента взаимной корреляции примет следующий вид:

s = 1 0 e ^ф + n _| e ^{V |},                            (1)

5 2 = 1 0 e ^(ф+ d sin ^e) + N 2 e i ^V 2 ,                            (2)

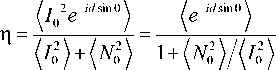
Отсюда видно, что модуль коэффициента корреляции будет определять соотношение сигнал/шум:

где I ₀ — интенсивность некого источника, N ₁, N ₂ —

интенсивности шумов, возникающих в приемных трактах. Фазы φ и ψ изменяются в пределах от 0 до 2π и не зависят друг от друга. Мощность сигнала в

mod ( n ) =

^, N 0² I 0²

одном из приемников можно записать следующим

образом:

P = ( s 1 s ;) = (( 1 ₀ e“ » + N 1 e^ )( I ₀ e ^{- , ф} + N 1 e "^ )) = = ( / ₀ ² + 1 ₀ N _| е ' ^{(ф-ф |} ) + 1 ₀ N 1 e^{i (V | -ф)} + N^,

а его аргумент — направление прихода волны: arg(η) = – d sinθ.                                (11)

где угловые скобки обозначают операцию усреднения. Поскольку фазы сигнала и шума независимы, при усреднении второй и третий члены суммы обратятся в нуль, и тогда выражение (3) будет иметь следующий вид:

P \I 0 / + \ N 1 /.

Для второго приемника можно записать аналогичное выражение

P 2 \I 0 / ⁺ \ N 2 /.

Для двух сигналов можно вычислить коэффициент взаимной корреляции

n =

/s s *\

S ₁ S ₂

Jpp PP 21

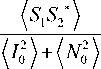
где

Подставив (1) и (2) в (6), получим

n =

(( 1 ₀ e ^ + N 1 e' ^V i )( 1 ₀ e ^{- , (ф+} d ^{sin 6)} + N ₂ e - i ^ ^ )}

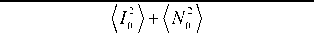
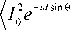
+ 1 ₀ N 1 e' ^{| -ф}- d ^{sin 6)} + 1 ₀ N ₂ e^{, (,-V} 2 ) + N 1 N ₂ e' ^{| -V} 2 )

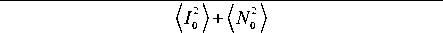
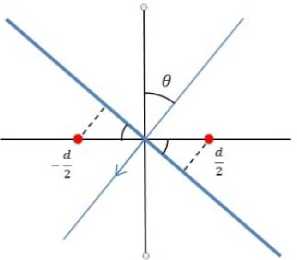
Рис. 1п. Геометрия эксперимента