Интерпретация данных капиллярных исследований

В петрофизике наиболее распространенным методом изучения капиллярных сил является исследование зависимости насыщенности пород от капиллярного давления Р_к = f K в (кривая капиллярного давления). Существуют различные методы получения капиллярной кривой. Основными методами измерения капиллярного давления являются метод капилляриметрии (полупроницаемой мембраны) и метод центрифугирования.

Метод капилляриметрии является наиболее распространенным и широко применяемым. Он основан на измерении содержания воды в капилляриметре при вытеснении воды из образцов горной породы нефтью или воздухом при различных перепадах давления. Такой способ нередко называют способом восстановления начального состояния системы, так как в опыте моделируется процесс вытеснения воды при заполнении ловушки нефтью или газом. Данный метод требует довольно большого количества времени проведения опыта - от двух недель до нескольких месяцев, а также не подходит для образцов трещинного, кавернозного и кавернозно-трещинного типов.

Метод центрифугирования, который основан на вытеснении свободной воды из образцов горной породы под действием центробежных сил, в отличие от метода капилляриметрии достаточно простой и быстрый.      Он      заключается      в центрифугировании насыщенных водой образцов и взвешивании их до и после центрифугирования, где затем определяют объем воды, оставшейся в керне [16]. Стоит отметить, что метод центрифугирования не подходит        для        исследования слабосцементированных образцов, которые разрушаются в ходе эксперимента. В настоящее время всё чаще используют высокоскоростные       ультрацентрифуги, которые позволяют проводить массовые лабораторные исследования и обеспечивают необходимую точность.

Существенным моментом, искажающим результаты      истолкования      данных капилляриметрии, является то, что зачастую величины капиллярного давления не приводятся к пластовым условиям (рис. 1). Вследствие этого значения капиллярного давления получаются завышенными и вносят значительные искажения в результаты интерпретации      данных.      Значения капиллярного давления, полученные в атмосферных условиях ( Pкатм ), к пластовым (Ркпл) приводятся по следующей формуле [2]:

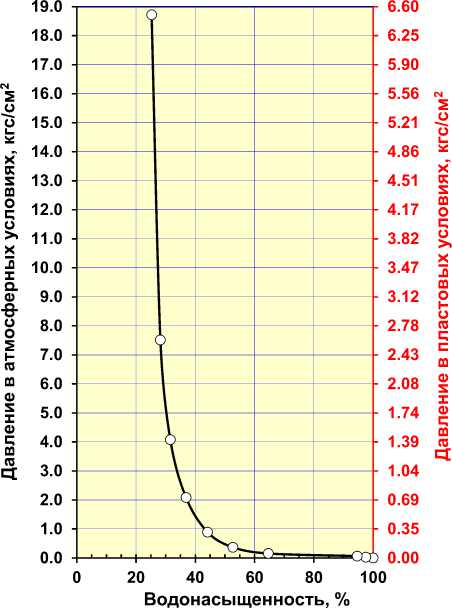
Рис. 1. Кривая капиллярного давления

пл кпл катм , где – поверхностное натяжение в пластовых условиях, зависит от насыщающего флюида, на границе вода-нефть в среднем составляет 25 дин/см; атм – поверхностное натяжение в атмосферных условиях, на границе вода-воздух составляет 72 дин/см [2].

Целью данной работы является иллюстрация интерпретации данных, полученных при изучении капиллярных характеристик на ультрацентрифуге.

Методика расчёта поровых каналов и их долевого участия в фильтрации жидкости

По результатам проведенных экспериментальных исследований методом капилляриметрии или центрифугирования получают зависимости насыщенности от капиллярного давления Pкf Kв для каждого образца породы. Связь между капиллярным давлением и структурой порового пространства является выражением поведения флюида в породе и определяется с учетом свойств породы и флюида по формуле Лапласа:

2 cos Q р =-----—

, к       Rк где       Рк - капиллярное       давление;

о - поверхностное натяжение на границе раздела фаз;     Q - угол увлажнения;

R к - радиус капилляра (поры).

На    основании    экспериментально получаемых зависимостей  Pкf Sв   по вышеприведенной формуле рассчитываются функции распределения пор по размерам для каждого исследованного образца коллектора.

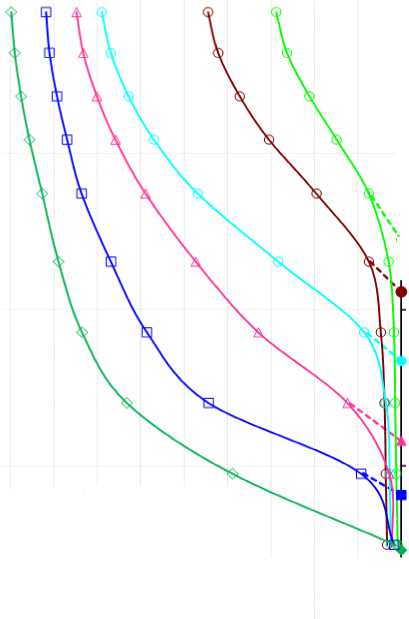
Для более наглядного представления рассмотрим расчёт размера поровых каналов и их долевого участия в фильтрации жидкости на образцах с различной проницаемостью. На первоначальном этапе определяем давление сдвига (давление, с которого начинается вытеснение жидкости). На рис. 2 приведён графический пример определения давления сдвига.

Для вычисления размера поровых каналов и их долевого участия в фильтрации жидкости расчёт удобно вести по представленной ниже схеме (табл. 1, 2).

В первые два столбца таблицы заносятся значения давлений ( P ) и водонасыщенности ( K _{в i} ). В первой ячейке указывается давление сдвига (отмечено синей заливкой в табл. 1, 2), которое необходимо для вычисления долевого участия поровых каналов в фильтрации жидкости. Далее вычисляются размеры поровых каналов ( R_i ) по формуле

2 cos Q 2 72 1

R 58,94 мкм.

ⁱ P_i 0,024

Размер поровых каналов, соответствующий давлению сдвига является максимальным радиусом (отмечено желтой заливкой в табл. 1, 2).

При значениях давлений, меньших давления сдвига, коэффициент давления принимается равным нулю (отмечено зелёной заливкой в табл. 1), так как в данном случае вытеснения жидкости не происходит, а уменьшение водонасыщенности связано с присутствием открытых пор на поверхности образца, откуда и происходит отток свободной воды.

Долевое участие поровых каналов в фильтрации жидкости находится по формуле

R ф i  100

1942 511

1942,511    _5,099%.

38094,130

На основании полученных данных строится распределение поровых каналов и их долевое участие в фильтрации жидкости (рис. 3).

Между давлением сдвига ( P0 ) и абсолютной проницаемостью по газу ( K ) наблюдается довольно хорошая зависимость (рис. 4). Сопоставление P0 с Kпр г выполнено для одного из месторождений Западной Сибири.

- 3.430

0.095

0.070

1.168

0.259

0.612

0.490

0.049

0.024

0.010

=^ Обр. 1 - 46, к _пр = 0,1 мД —- Обр. 1 - 16, к _пр = 0,3 мД ^- Обр. 1 - 45, к _пр = 0,7 мД — Обр. 1 - 28, K _пр = 2,3 мД ^ Обр. 1 - 19, K _пр = 15,1 мД

Обр. 1 - 30, к_ = 107,9 мД

0    10   20   30   40   50   60   70   80   90   100

Водонасыщенность, %

24.010

К <  4 M Ct

Рис. 2. Пример графического определения давления сдвига для образцов с различной проницаемостью

Таблица 1

Пример вычисления размера поровых каналов и их долевого участия в фильтрации жидкости.

Образец 1-46, K 0,1 мД

о X о" К о R со cd 1,168 0,026	ед н о о и m 100,00	со ё о 2 О “5 К да s S 1,23	Конечные размеры поровых каналов R , мкм >55,18		X 2 ед к о о * 0,83	-е- у « 4 0,000	K i V i 0,000	ед со      ^ 5 о S    5 ^ 5 н В ^ да  Н  6  g О У S Й Р-1 у ^ И К ^   ^ 0,000
	99,17	55,18	55,18	22,70	0,33	0,000	0,000	0,000
0,063	98,84	22,70	22,70	9,41	0,25	0,000	0,000	0,000
0,153	98,59	9,41	9,41	3,90	0,27	0,000	0,000	0,000
0,369	98,32	3,90	3,90	1,62	1,23	0,000	0,000	0,000
0,890	97,09	1,62	1,62	0,69	4,57	0,746	3.412	70,6821
2,080	92,52	0,69	0,69	0,35	7,42	0,146	1.080	22,3781
4,078	85,10	0,35	0,35	0,21	6,27	0,040	0.253	5,2342
7,000	78,82	0,21	0,21	0,12	5,17	0,014	0.071	1,4646
12,000	73,65	0,12	0,12	0,07	2,46	0,005	0.012	0,2409
20,000	71,19	0,07	<0,07		71,19	0,000	0.000	0,0000
Сумма:					100,00		4,828	100,00

Таблица 2

Пример вычисления размера поровых каналов и их долевого участия в фильтрации жидкости. Образец 1-30, K 107,9 мД

о	н к да ^ К	со 5 Ct Он о да да Сс W	Конечные размеры поровых каналов R , мкм		X! m ^ & ^ 2 « с о О “	5 ^~ S	K i V i	Дед   ^ 5          - 5^3^ w 2 a s з    й о ед н ч g Д ^   ^
0,024     100,00		58,94	58,94	55,18	1,24	1571,828	1942,511	5,09924
0,026	98,76	55,18	55,18	22,70	37,66	858,467	32328,080	84,86368
0,063	61,11	22,70	22,70	9,41	24,29	145,660	3537,775	9,28693
0,153	36,82	9,41	9,41	3,90	10,35	25,026	259,083	0,68011
0,369	26,47	3,90	3,90	1,62	5,43	4,301	23,344	0,06128
0,890	21,04	1,62	1,62	0,69	3,76	0,746	2,807	0,00737
2,080	17,28	0,69	0,69	0,35	2,94	0,146	0,428	0,00112
4,078	14,33	0,35	0,35	0,21	1,94	0,040	0,078	0,00021
7,000	12,39	0,21	0,21	0,12	1,45	0,014	0,020	0,00005
12,000	10,94	0,12	0,12	0,07	0,78	0,005	0,004	0,00001
20,000	10,16	0,07	<0,07		10,16	0,000	0,000	0,00000
Сумма:					100,00		38 094,130	100,00

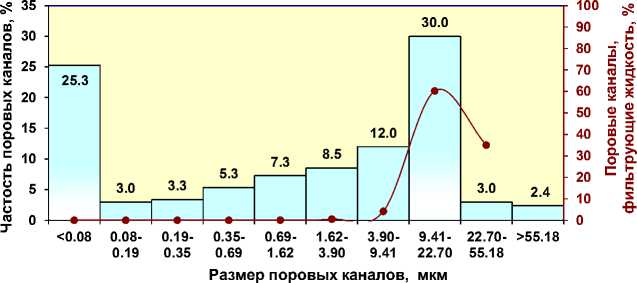
Рис. 3. Распределение поровых каналов по размерам и их участие в фильтрации жидкости

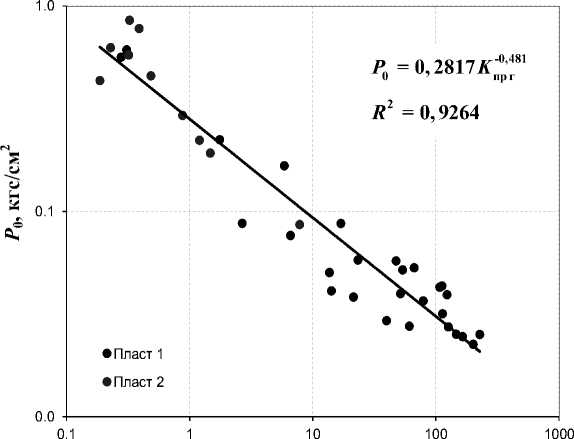
K пр г , мД

Рис. 4. Сопоставление давления сдвига ( P ) с абсолютной проницаемостью по газу ( K )

Расчёт радиусов поровых каналов

Одним из важных показателей в области петрофизики являются размеры пор и поровых каналов и характер их распределения по величинам (см. рис. 3). От этих показателей во многом зависит распределение фаз в коллекторе. Такие петрофизические параметры, как абсолютная проницаемость, фазовые проницаемости и остаточная нефтенасыщенность продуктивных пластов, зависят преимущественно от размера поровых каналов, из которых слагается поровое пространство. Поэтому изучению структуры, строения и размеров фильтрационных каналов уделяется большое внимание [17, 18, 20-23]. Известно, что чем более неоднородны размеры поровых каналов коллектора, тем больше остаточная нефтенасыщенность и тем меньше коэффициент вытеснения. Это явление в глинизированных коллекторах обусловлено прежде всего эффектом Лапласа.

При применении различных кольматантов для создания непроницаемых фильтрационных корок, которые изолируют поровые каналы в пластах открытого ствола скважины, очень важно верное представление о средних радиусах фильтрующих каналов ( R _срф).

На сегодняшний день существует множество формул по определению среднего радиуса поровых каналов. Основные из них были предложены Ф.И. Котяховым и

Б.И. Тульбовичем, также их выводят из формул Дарси и Пуазейля.

Средний радиус пор реальных пористых сред,    предложенный    Ф.И. Котяховым, рассчитывается по следующей формуле [9]:

20  0,5035 Kпр ср    7         K 2,1     , где K – коэффициент газопроницаемости;

К_п - коэффициент пористости.

Б.И. Тульбовичем для нахождения среднего ( R ) и среднего эффективного

( Rср эф ) радиусов поровых каналов, были предложены следующие уравнения [14]:

Log K пр   2,34

^R ср   ¹⁰

R , R ср эф

;

4,41

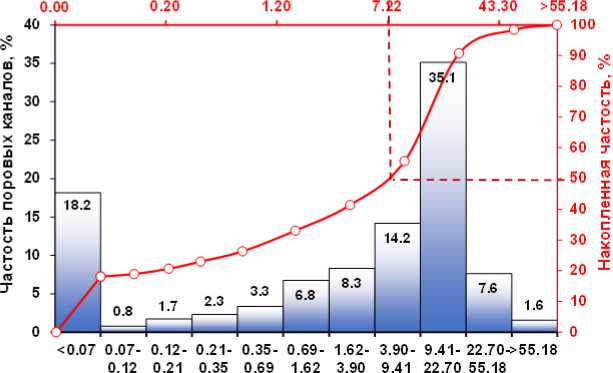
2 8 K пр 10^3T

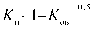
где T – извилистость поровых каналов;

K _ов - остаточная водонасыщенность.

С учётом законов Дарси и Пуазейля формулы недостаточно точны для практического применения, поскольку они не учитывают распределения поровых каналов по размерам [1].

Методика вычисления радиусов поровых каналов по методу кумулятивной кривой

Наиболее простым способом является метод кумулятивной кривой, где радиусы поровых каналов характеризуют с помощью медианы ( M ). Для получения медианы графическим методом строится кумулятивная кривая. Через ординату, соответствующую 50 %, проводят горизонтальную линию до пересечения с кумулятивной кривой. Абсцисса, отвечающая ординате 50 % называется медианой ( M ) (рис. 5).

Для вычисления среднего радиуса математическим способом расчет удобно вести по представленной ниже схеме (табл. 3).

Средние радиусы поровых каналов вычисляются по приведённым ниже формулам. Средний радиус поровых каналов, средний радиус поровых каналов находится мкм:

по формуле

R ср

20   K пр

.

7    K п

Однако    множественный    анализ

лабораторных

данных показал, что эти

^R ср    ^yi 50

l i 50    50 h i 50

l 1 50    l 1 50

3,90

58,57  50  5,51

58,57  44,36

7,22.

Размер поровых каналов, мкм M ( R ср), %

Размер поровых каналов, мкм

Рис. 5. Графический метод определения среднего радиуса поровых каналов

Таблица 3

Конечные размеры поровых каналов R , мкм		£ x К й X У О Щ о -~ 5 c ^ ~ pq co Й    o 8 5 S 8 Cd g * P^ Ph	X 5 о *	2 Й cd § P<2 § g § 5 cd 5 R s g К	щ ^ bQ PQ о а с	н X ^ ° 3 - О щ ^& о « ^ cd S И У X § s g § 5 Г) « cd cd X Ри 3 Н tQ О Щ Ю Ри S ° с	X PQ С PQ & g М ^ Н 2 S о 5 5 cd 2 У И 5 г^ -&	X л  3  -^ Н PQ  ^ о о g о к я с а 5 н g о g ®  cd  5 м S & 2 ” S S ” я " 5
55,18	55,18	0,00	1,58	1,58	1,94	1,94	0,00	0.00000
55,18	22,70	32,47	7,65	9,23	9,35	11,28	54,36	54.35597
22,70	9,41	13,29	35,12	44,36	42,92	54,20	42,36	96.71233
9,41	3,90	5,51	14,21	58,57	17,37	71,57	2,945	99.65709
3,90	1,62	2,28	8,32	66,89	10,16	81,74	0,296	99.95325
1,62	0,69	0,93	6,75	73,64	8,25	89,99	0,042	99.99497
0,69	0,35	0,34	3,34	76,98	4,08	94,07	0,0040	99.99899
0,35	0,21	0,15	2,33	79,31	2,85	96,92	0,0008	99.99977
0,21	0,12	0,09	1,74	81,05	2,13	99,05	0,00020	99.99997
0,12	0,07	0,05	0,78	81,83	0,95	100,00	0,00003	100.00000
0,07	0,04	0,04	18,17	100,00	0,00	100,00	0,00000	100.00000
Сумма			100,00		100,00		100,00

Пример вычисления средних радиусов поровых каналов по методу кумуляты (кумулятивной кривой). Образец 1-19, K 15,1 мД

Средний радиус эффективных поровых каналов, мкм:

l _{эф i 50}    50 h_i> 50

R ср эф    y i >50

^эф 1 50      ^эф 1<50

9,41 +

54,20  50 13,29

^{,              ,}       10,71.

54,20  11,28

Средний радиус поровых каналов по

долевому    участию    в

фильтрации

жидкости, мкм:

l _{ф i 50}    50    h_i >50

R _ср     y_i >50        ^{i 50}

^ф 1 50      ^эф 1<50

22,70+

54,36  50 32,47

54,36  0

25,31.

Метод квартилей не является универсальным. Он пригоден для наиболее грубой и приблизительной оценки радиусов

поровых каналов.

Методика вычисления радиусов

вычисление радиусов поровых каналов по методу статистических моментов. Метод моментов    базируется    на    строгой вероятностной     теории      оценивания статистических характеристик.

Расчёт средних радиусов реализован по представленной ниже схеме (табл. 4).

Средние радиусы поровых каналов вычисляются по приведённым ниже формулам. Средний радиус поровых каналов, мкм:

s V i l i

^R ср    ^{2     Vi}    2 ^1,516    2,86.

ср

Средний радиус эффективных поровых каналов, мкм:

V эф _i l i

R ср эф    2 ¹ V эф i    ₂ 2,787    6,90.

Средний радиус поровых каналов по долевому    участию    в    фильтрации

жидкости, мкм:

поровых каналов по методу статистических моментов

Математически более строгим, чем метод кумулятивной кривой, является

R срф

X ^R ср ф i ^l i R срф i

2 4,653   25,16.

Таблица 4

Пример вычисления средних радиусов поровых каналов по методу статистических моментов. Образец 1-19, K 15,1 мД

Конечные размеры поровых каналов R , мкм		gig g В 5 co 1-1 -S4 о Й s Д О Р Щ S 2 U Рн	X д ^ 2 д о *	« ^ 1 § г^ д СП м S й О ^ с	2 у д ^ S S о    S м 3 5 pq Рн Ч О Й « 2 s
55,18	55,18	- 5,79	1,58	1,94	0,00	- 9,16	- 11,20	0,0
55,18	22,70	- 5,28	7,65	9,35	54,36	- 40,41	- 49,38	- 287,2
22,70	9,41	- 4,01	35,12	42,92	42,36	- 140,68	- 171,92	- 169,6
9,41	3,90	- 2,73	14,21	17,37	2,945	- 38,87	- 47,50	- 8,05
3,90	1,62	- 1,46	8,32	10,16	0,296	- 12,18	- 14,88	- 0,43
1,62	0,69	- 0,21	6,75	8,25	0,042	- 1,40	- 1,71	- 0,009
0,69	0,35	0,94	3,34	4,08	0,0040	3,13	3,82	0,0038
0,35	0,21	1,84	2,33	2,85	0,0008	4,29	5,24	0,0014
0,21	0,12	2,62	1,74	2,13	0,00020	4,56	5.57	0,0005
0,12	0,07	3,38	0,78	0,95	0,00003	2,64	3,22	0,0001
0,07	0,04	4,21	18,17	0,00	0,00000	76,51	0,00	0,0000
Сумма			100,00	100,00	100,00	- 151,58	- 278,74	- 465,31

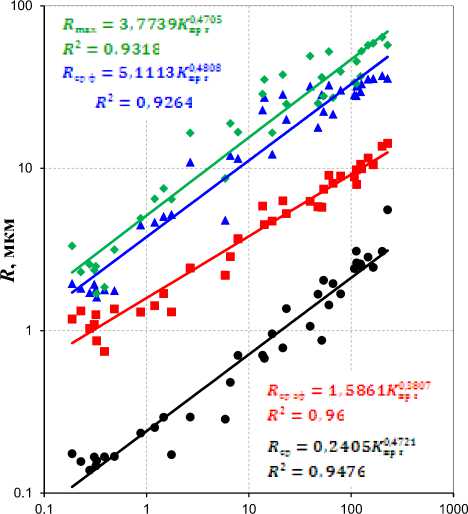
K пр г , мД

Рис. 6. Сопоставление среднего ( R ), среднего эффективного ( R ), среднего по долевому участию в фильтрации ( R ) и максимального ( R ) радиусов поровых каналов с абсолютной проницаемостью по газу ( K )

Между радиусами поровых каналов ( R ) и K    существует степенная зависимость

(рис. 6). Сопоставление R с K _прг выполнено для одного из месторождений Западной Сибири.

Расчёт относительных фазовых проницаемостей по данным капилляриметрии

Фазовые проницаемости являются важнейшими характеристиками фильтрации пластовых флюидов в пористой среде, они практически полностью определяют процесс течения     пластовых     флюидов     в породах-коллекторах нефти и газа. Данные о фазовых проницаемостях необходимы при обосновании кондиционных пределов петрофизических свойств породы, при промышленной оценке переходных нефтегазовых зон пластов, в газогидродинамических расчетах технологических показателей разработки, при выборе методов воздействия на пласт с целью увеличения нефтеотдачи, при анализе и контроле за разработкой залежей. Учитывая огромную значимость этих функций, важно уделить особое внимание методам их расчета различных геолого-технических мероприятий и методов увеличения нефтеотдачи, проводимых на объекте [5]. Следовательно, применять эти методы следует только в качестве первоначального приближения при макронастройке моделей на историю разработки.

В связи с отмеченным основным источником данных об ОФП являются лабораторные методы, основанные на исследованиях, которые проводятся на керне. Известны три основных метода получения кривых ОФП на керне:

• -    определение ОФП в режиме стационарной фильтрации;

• -    установление ОФП в режиме нестационарной фильтрации в процессе вытеснения одного флюида другим;

• -    расчёт ОФП по кривым капиллярного

давления.

Уравнения для расчёта ОФП

Относительные фазовые проницаемости для смачивающей (воды) и несмачивающей фаз (нефть, газ), построенные на базе капиллярной модели Пурцелла, были предложены Бурдайном и имеют следующий вид [2]:

получения.

Методы получения информации об относительных фазовых проницаемостях можно условно разделить на две категории: лабораторные (эмпирические) и аналитические.

в пр отн

н

K пр отн

( K .- K ов f K f d K Ж

I 1- K « J 0 P ; 0 рГ

' I- K в- K он Y ¹ d K 'd K 11- K о, -к K в Р к  0 P ^2,

К аналитическим относятся методы, где Pк – капиллярное давление; Kв – текущая использующие в качестве исходных данных результаты гидродинамических исследований скважин (ГДИС) или промысловые данные. Несмотря на общепринятое мнение о преимуществе аналитических методов [3-5, 7, 8, 10-13, 15], практический опыт показывает, что у них существуют недостатки: невозможность получения данных для всего диапазона возможных изменений флюидонасыщенности и термобарических условий пласта [4], влияние на результат водонасыщенность;         Kов – остаточная пластовая

вода;        K _он – остаточная

нефтенасыщенность.

Скобки перед отношением интегралов, по мнению автора, введены для учёта несоответствий между реальной средой и её капиллярной моделью. Между тем простой анализ выражений, содержащихся в скобках, позволяет сказать, что прежде всего они ограничивают существование проницаемости фаз в определённых объёмах порового пространства. У смачивающей фазы проницаемость равна нулю при Kв Kов , а у несмачивающей при Кв = 1 - Кон.

Значения K _ов и K _он и дроби перед интегралами в значительной степени определяют форму кривых относительной проницаемости. Поэтому существует много инженерных формул, в которых отношением интегралов пренебрегают [6].

По данным фирмы Шлюмберже (1989 г.), экспериментальные кривые    проницаемости    определяются уравнениями [6]:

к вротн= [1- к в -к он / 1- к ов- к он Г';

K Протн= [ 1- K в / 1- K о. Г

В случае фильтрации газа и воды Ботменом были предложены следующие уравнения [19]:

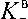
пр отн

г

K пр отн

= 1- K в

1- к _в ⁰,²⁵

/ X 0,25 П0’5

P н

показатель смачиваемости ( M ), и, как следствие, для гидрофобных пород будут наблюдаться существенные расхождения в относительной фазовой проницаемости по воде ( K _п ^в _ротн ), полученной экспериментально и по кривым капиллярного давления (рис. 7).

С целью учёта M в гидрофобном коллекторе, вышеуказанные уравнения K _п ^в _{р отн} нами были умножены на M . Например, K _п ^в _{р отн} , по данным фирмы Шлюмберже, будет иметь следующий вид:

0,5

K роти =Г 1- К в- К н / 1- К в- К он Т’¹ -пр отн в он ов он

После учёта M в уравнении K _п ^в _{р отн} наблюдается лучшая сходимость между K _п ^в _{р отн} , полученной экспериментально и по кривым капиллярного давления (рис. 8).

Из вышесказанного следует, что для гидрофобного коллектора уравнения K _п ^в _{р отн} целесообразно дополнять M .

где P _н – параметр насыщения.

Следует     отметить,     что     все вышеприведённые формулы не учитывают

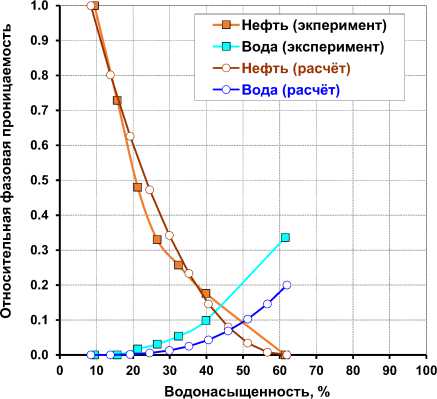
Рис. 7. Относительные фазовые проницаемости

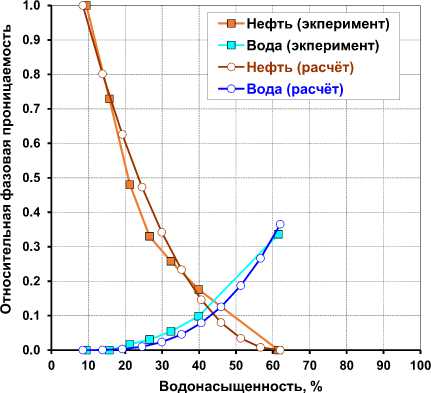
Рис. 8. Относительные фазовые проницаемости

Статистическая обработка результатов капилляриметрии

В петрофизике объяснить поведение многофазных систем без исследования капиллярного давления и смачиваемости пород не представляется возможным. Характер распределения пластовых флюидов всецело зависит от физико-химических свойств горных пород и насыщающих их флюидов. Как правило, образец, на котором изучают капиллярное давление, представляет собой лишь элементарный (очень маленький) объем пласта. Оценивать свойства пластов и выполнять необходимые расчеты по отдельным образцам невозможно. Поэтому все образцы пласта должны быть определенным образом разбиты на группы в соответствии с их величинами капиллярного давления, проницаемости и пористости. Для этих целей используют два метода корреляции данных капиллярного давления:

• 1)    коррелирующую функцию JK _в ,

где Pк – капиллярное     давление;       – поверхностное      натяжение;      K – проницаемость пород; Kп – пористость в долях единицы.

Для построения модели месторождения необходимо       проводить       расчеты коэффициентов насыщенности пород на разных высотах над уровнем свободной воды. Такой расчет можно проводить, используя зависимость    безразмерной    J-функции

Леверетта        от        коэффициента водонасыщенности     ( Kв ).     J-функция

Леверетта позволяет обобщить значения капиллярного давления по образцам с различными значениями пористости и проницаемости.

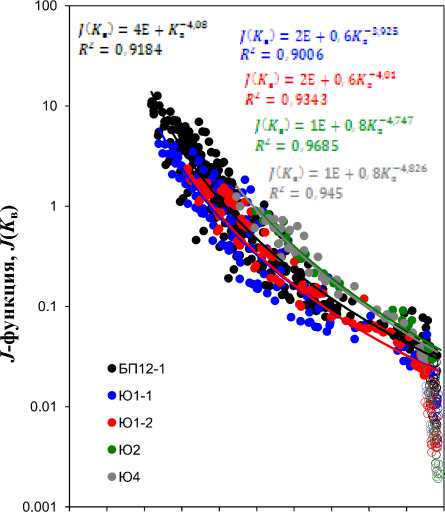
Результаты обработки капиллярных давлений по первому методу были выполнены для группы пластов одного из месторождений

Западной Сибири. Результаты представлены на рис. 9, где отчетливо выделяются три предложенную М.С. Левереттом [2]:

JK в

P к

а

K пр K п

А1/2

группы пород по форме капиллярных кривых: пласт БП12-1; пласты Ю1-1 и Ю1-2; пласты Ю2 и Ю4.

0   10   20   30   40   50   60   70   80   90  100

K в , %

Рис. 9. Функция капиллярного давления для группы пластов

• 2)    статистический метод, разработанный Р.К. Гутри [2] :

Второй метод оценки данных капиллярного давления используется для вычисления насыщенности пород всего пласта фазами в зависимости от их проницаемости для постоянных значений капиллярного давления. Результаты анализа представлены на рис. 10 и 11.

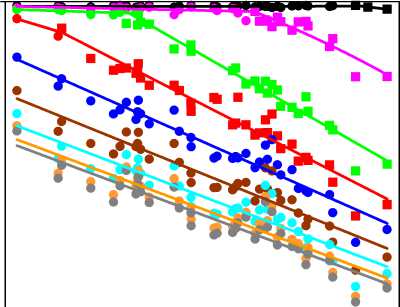
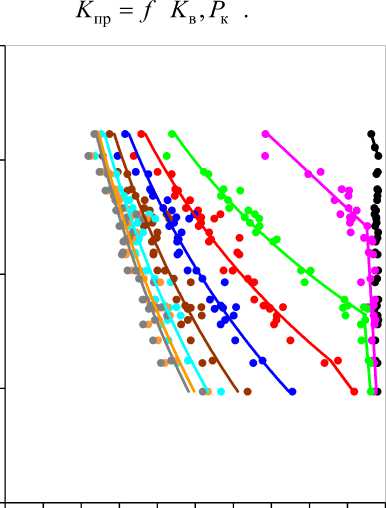
Графики на рис. 10 характеризуют зависимость величины коэффициента водонасыщенности ( Kв ) коллекторов пласта проницаемости по газу ( log Kпр ) при различных значениях капиллярного давления ( Pк ), а графики на рис. 11 – зависимость величины коэффициента абсолютной проницаемости по газу ( Kпр ) от коэффициента водонасыщенности ( Kв ). Расчёт Kв и K производится по полученным зависимостям, приведённым на рис. 10 и 11:

K в f log K пр , P к ;

БП12-1    от    логарифма    абсолютной

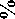
-0.1 0.1 0.3 0.5 0.7 0.9 1.1 1.3 1.5 1.7 1.9 2.1 2.3

Ч S 10

0.1

0  10  20  30  40  50  60  70  80  90 100

K в , %

^К = = I° _|flti.46SK_T           = Б ;е-ю^

^ч : - ZE-lZe"024^ I KEf :" =;Е + 11^

^ =:2 Е 12К_^ ^=4Е + 12^

Log K пр

К ; =<),06331^^ - ну 17,597 1^7 = 94 941е"^:"⁴^

*■ - 9. а848Log К.^   117,5,"I К. = 73,332в~*уве L^K4

F - ^-3- 142LgeK - 140 55Я К, = 5 2,8 6 Эе"*™ '■’^ч

Кч : = IE - 56e-:l LZLK-K=F = 2 3 661e"""F-

^Л ^=-2.53931^^+95.99 ^ = 49.3 09^”^ кТ^Т^З^зГ⁷^^^ ^ ^^дз^-цзи^л., К, = 90 966а-^№ l^

A=F := бЕ + 37^™7^ А^ -3lE-lZK7^ ОК,-^" I КЧ=ЗЕ + 12К.-^

К„ = 12407e-*wjr'

• •    F_v= O.OLL

•Fv= 0.156

• •    F_v= 1.726

•^= 0.02;

• •    F_v= 0.37;'

•Fv= 2,77!3

•Fv= 0.065

•Fv= 0.881

•J\= 3.472

•Fv= 0.01JL

•Fv= 0,156

•Pv= 1.726

•F,= 0.027

•P„= 0.377

•Fv= 2,778

•Fv= 0,065

•Fv= 0.881

•Fv= 3,472

Рис. 10. Зависимость водонасыщенности ( K ) от логарифма газопроницаемости ( log K ) для различного капиллярного давления ( P _к , кгс/см²) пород пласта БП12-1

Рис. 11. Сопоставление газопроницаемости ( K ) и водонасыщенности ( K _в ) для различного капиллярного давления ( P _к , кгс/см²) пород пласта БП12-1

Зависимости на рис. 10 и 11, полученные для величин капиллярного давления 0,011, 0,027, 0,065 и 0,156 кгс/см ² , описываются двумя уравнениями (первое уравнение для точек в виде круга, а второе уравнение, помещенное в рамку, для точек в виде квадрата).

Зависимости на рис. 11, полученные для коллекторов пласта БП12-1, свидетельствуют о следующем:

• 1)    при P _к 0, 011 кгс/см² вытеснение жидкости начинается с K _пр 110 мД;

• 2)    при P _к 0, 027 кгс/см² вытеснение жидкости начинается с K 25 мД;

• 3)    при P _к 0, 065 кгс/см² вытеснение жидкости начинается с K 5 мД;

• 4)    начиная с P 0,156 кгс/см² , к

вытеснение жидкости происходит во всём диапазоне K _пр .

Заключение

Данные порометрических исследований, которые получают в атмосферных условиях, необходимо приводить к пластовым с учетом поверхностного натяжения на границе раздела двух фаз.

Поровые каналы, фильтрующие жидкость, рассчитанные с использованием давления вытеснения повышают точность результатов, так как исключают открытые поры на поверхности образца, откуда происходит отток свободной воды.

Средние радиусы поровых каналов, полученные по данным порометрических исследований, учитывают распределение поровых каналов по размерам и, как следствие, повышают достоверность полученных данных.

При подборе кольматантов для создания непроницаемых фильтрационных корок средний радиус фильтрующих каналов окажет существенную помощь.

Для гидрофобного коллектора уравнения относительной фазовой проницаемости по воде целесообразно дополнять показателем смачиваемсти пород.

Все полученные данные окажут неоспоримую помощь при построении различных моделей и технологических схем, а также способствуют уточнению расчетной модели пласта в процессе разработки.