Интерпретация перехода жидкость-стекло в рамках квантовой механик

Известно, что все аморфные вещества независимо от их природы (неорганические стекла, аморфные органические полимеры, металлические аморфные сплавы) в области стеклования подчиняются общим универсальным закономерностям [1–4], в частности, они переходят из жидкого (высокоэластического) в твердое стеклообразное состояние практически при одной и той же вязкости

n (T g ) ~ const ® 10 12 Па - с.

При размягчении стекла появляются состояния, не характерные для стеклообразных твердых тел [5-7]. Удается объяснить ряд явлений в области перехода жидкость-стекло, если предположить, что в стеклообразующих жидкостях имеется возбужденное состояние, отличающееся от основного состояния избытком энергии. Например, для расплава стеклообразного B 2 O 3 такой избыток энергии составляет 21 кДж/моль [7].

Квант энергии делокализации атома и частота его колебаний

• 1.    Будем полагать, что низкая вязкость и лабильность стеклообразующего расплава выше температуры стеклования T g обусловлены наличием делокализованных возбужденных атомов, которые рассматриваются как квантовые осцилляторы с квантом энергии возбуждения – энергии делокализации [8]

• 2.    Значения частот, вычисленные по формуле (2) с привлечением постоянной D для различных аморфных веществ (табл. 1),

  v = Ag/ h = kD/h « (1.2 - 5.3) - 10¹³ Гц,                             (8)

• 3.    Температурный интервал концентрации делокализованных атомов (3) можно разбить на две области: высокотемпературную ( kT>> Ag _e = h v ), где exp( h v /kT) « 1+( h v /kT) ,

  N e N

  
  
  

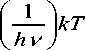
Ag e = h v .

Под делокализацией атома подразумевается его критическое смещение из равновесного положения, соответствующее точке перегиба на кривой потенциала U(r) , иначе, максимуму силы межатомного взаимодействия (рис. 1) [1]. В результате критических флуктуационных смещений частиц из равновесных положений возникает флуктуационный объем аморфной среды: A V e = N e Au e , где N e -число делокализованных атомов, Au e - элементарный флуктуационный объем, необходимый для делокализации атома.

При охлаждении стеклообразующего расплава относительное число делокализованных атомов N_e/N уменьшается в соответствии с соотношением [8, 9]

N e N

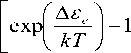
-1

Температурная зависимость свободной энергии активации вязкого течения стеклообразующих жидкостей A F _n (T) определяется в основном зависимостью от температуры концентрации делокализованных атомов (3) [9]

A F  A F ■ bkT

—

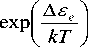
где A F _Z - высокотемпературный предел свободной энергии активации, b - коэффициент, учитывающий перекрытие микрообъемов Au e , он близок к единице: 0.5 <  b <  1.

Эта формула (4) практически совпадает с эмпирическим выражением [9]

AF„ = kB + kC exp l — | , ⁿ          \T)

которое вытекает из сравнения уравнений вязкости Эйринга [10] и Енкеля [11, 12]. Здесь B , C и D – параметры уравнения Енкеля, k – постоянная Больцмана. Меерлендер [12] в результате сравнения наиболее распространенных эмпирических уравнений вязкости (Фогеля-Фульчера-Таммана, Уотер-тона и др.) пришел к выводу, что из них соотношение Енкеля более точно и лучше описывает опытные данные в широком интервале температуры.

Из равенств (4) и (5) видно, что величину Ag e можно рассчитать на основе экспериментальных данных об эмпирическом параметре уравнения Енкеля D (табл. 1): Ag e = kD . Например, энергия делокализации атома для щелочносиликатного стекла ( D = 2500 К [12])

Ag e = kD = 21 кДж/моль

находится в согласии с результатами расчета Ag e по соотношению модели делокализованных атомов [1] для ряда щелочносиликатных стекол

Ag e = kT g ln(1 f g ) = 17-23 кДж/моль,                                 (7)

где f g = (ΔV e /V) T=Tg – доля флуктуационного объема, замороженная при температуре стеклования T=T_g . Эти данные для Ag e близки к отмеченному выше избытку энергии возбужденного состояния стеклообразующей жидкости в сравнении с основным [7].

оказываются в области акустического спектра. У низкомолекулярных органических стекол (v = (1.22.0)-1013 Гц) и у аморфного органического полимера - полиизобутилена (v = 1013 Гц) они совпадают с частотами квантового размораживания вибрационной динамики макромолекул в области размягчения аморфных полимеров ПВА и ПЭТФ, определенными из спектров поглощения в ИК – области [2], v = (1.8^2.4)-1013 Гц.                                            (9)

Соответствующая область температуры возбуждения квантового размораживания вибрационной динамики макромолекул у этих полимеров совпадает с областью их стеклования [2].

В табл. 2 приводятся значения кванта энергии Age, вычисленные по формуле (7), и значения частоты v = Age/h колебаний возбужденных атомов для трех классов стеклообразных систем: аморфных органических полимеров, неорганических стекол и металлических аморфных сплавов. Как видно, они согласуются с приведенными выше данными (8) и (9). В частности, частоты для аморфных полимеров v = Age /h = (1.2^2.4)-1013 Гц                                       (10)

совпадают со значениями v для полимеров ПВА и ПЭТФ (9).

и низкотемпературную ( kT<< Ag e = h v ), где exp( h v /kT )>> 1,

N f-hv ]                                   (12)

I kT )

—— = exp N

Таблица 1

Эмпирические постоянные уравнения (5) и вычисленные из них характеристики вязкого течения и стеклования аморфных веществ ( ΔF_∞ = kB и Δε_е = kD )

Вещество	B	D	ΔF ∞	Δε е	v = kD/h ,	Литература
	K		кДж/моль		Гц
Силикатное стекло №15	13226	2500	110	21	5.3 - 1013	[12]
№18	13348	2500	111	21	5.3 - 1013	[12]
Na 2 O∙3SiO 2	-	1840	-	15	3.7 - 1013	[11]
Минеральное масло XII	1195	800	10	7	1.7 - 1013	[12]
XIII	928	700	8	6	1.5 - 1013	[12]
XIV	741	600	6	5	1.2 - 1013	[12]

XV	686	600	6	5	1.2 - 1013	[12]
XVI	615	600	5	5	1.2 - 1013	[12]
Глицерин	-	920	-	8	0.2 - 1013	[11]
Полиизобутилен	-	460	-	4	1 - 1013	[11]

Таблица 2

Параметры модели делокализованных атомов для аморфных органических полимеров, натриевосиликатных стекол и металлических аморфных сплавов (использованы данные [1, 8])

Аморфное вещество Tg, K fg lnf -1) 1 fg) ASe, кДж/моль 0 AUe, А 0, К с v, Гц Поливинилацетат 305 0.028 3.6 9 - 1084 0.28 2.2-1013 Натуральный каучук 300 0.026 3.6 9 - 1084 0.28 2.2-1013 Полистирол 363 0.030 3.5 7 39 843 0.29 1.7-1013 Полиэтилен 248 0.032 3.4 5 30 602 0.29 1.2-1013 Na2O-SiO2 (Na2O мол.%) 19.0 746 0.026 3.6 19 10 2289 0.28 4.6-1013 26.1 721 0.026 3.6 20 9 2410 0.28 4.9-1013 32.9 704 0.028 3.6 18 9 2169 0.28 4.4-1013 Fe83B17 760 0.026 3.6 23 - 2771 0.28 5.6-1013 Fe41.5Ni41.5B17 720 0.026 3.6 22 - 2651 0.28 5.4-1013 Pd82Si18 657 0.027 3.6 20 - 2410 0.28 4.9-1013 Pd40Ni40P20 602 0.026 3.6 18 - 2169 0.28 4.4-1013 fg =1/C1, где Ci - «универсальный» параметр уравнения Вильямса-Ландела-Ферри ([1]), величины Ase и c рассчитаны по формулам (7) и (16), а Ave - по соотношению Ave = kTg/fgB, где B - модуль объемного сжатия [1].

Таким образом, при высоких температурах концентрация делокализованных атомов N e /N линейно зависит от температуры (11), а при низких – она убывает чрезвычайно быстро по экспоненциальному закону (12).

Температуру 0, при которой высокотемпературная область переходит в низкотемпературную, назовем характеристической температурой. Она по аналогии с температурой Эйнштейна 0E находится из условия близости средней энергии теплового движения атома kT к кванту энергии Ase = hv k0 = hv,     0 = hv/ k = AsJ k.

Доля флуктуационного объема f g , замороженная при температуре стеклования, в первом приближении является постоянной величиной (у неорганических стекол, аморфных органических полимеров и металлических аморфных сплавов - металлических стекол): f_g ~ const ~ 0.026, откуда и логарифм ln(1/ f g ) принимает универсальное значение (табл. 2).

ln(1/ f_g ) ~ const ~ 3.6.

Поэтому из соотношений (7) и (13) следует, что температура стеклования пропорциональна характеристической температуре

T g = c 0 ,

где коэффициент пропорциональности равен (табл. 2)

с = 1/ ln(1 f g ) ~ const ® 0.3

Эмпирическая постоянная Енкеля D в уравнении (5) приобретает смысл характеристической температуры D = 0 ((6) и (13)), причем, как и следовало ожидать, между D и T_g наблюдается линейная корреляция (рис. 2): D ~ T g .

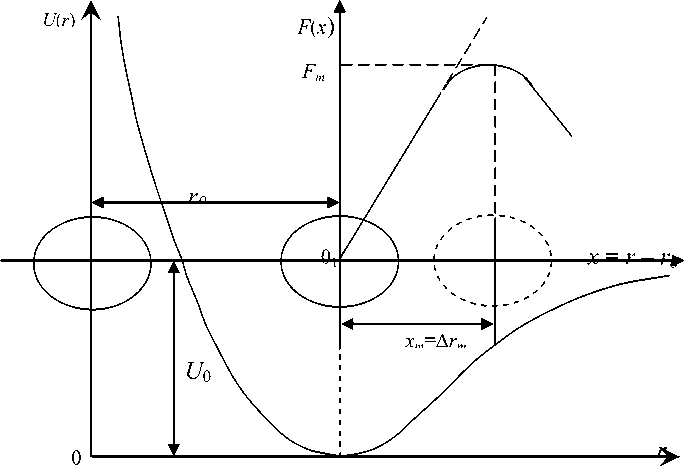
Рис. 1. Схема делокализации атома (схема возбуждения межатомной связи).

Ar m - критическое смещение (делокализация) атома, соответствующее максимуму силы межатомного взаимодействия F_m (перегибу кривой потенциала U(r) )

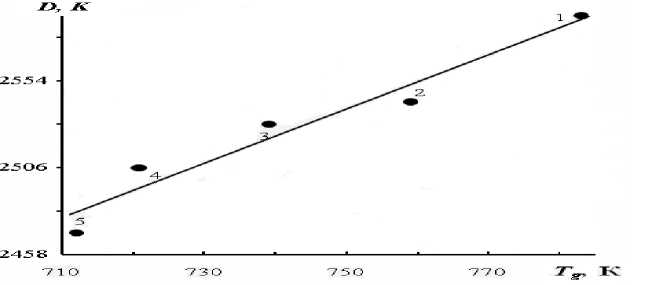
Рис. 2. Корреляция между параметром уравнения Енкеля D и температурой стеклования T_g натриевосиликатных стекол. Na₂O, мол.%: 1 – 15, 2 – 20, 3 – 25, 4 – 30, 5 – 33.3

Использование квантовой механики привлекательно в связи со своеобразным двухстадийным возрастанием средней энергии тепловых колебаний решетки [2, 13]. При T < 0.2 9 D , где 9 D - температура Дебая, тепловые колебания практически не возбуждены («заморожены»). Начиная с температуры

T « T g ~ 0.3 9 d ,

вибрационная динамика вступает в действие [2]. Здесь T_g – температура размягчения, равная температуре стеклования.

Как видно, формула (15) совпадает с равенством (17) при 9 =9d. Подставив в соотношение для концентрации делокализованных атомов (12) при T=Tg значение отношения h v kTg

^Ee kTg

= ln

fz ] x fg 7

const ^ 3.6 ,

вытекающее из выражений (2), (7) и (14), приходим к результату

N e )

N )

T = T g

= exp

I

h v

T >

const » exp( - 3.6) » 0.03 ,

который означает, что стеклование жидкости (аморфного полимера) есть следствие быстрого убывания («вымораживания») относительного числа делокализованных возбужденных атомов – квантовых осцилляторов до минимального значения (19), при котором достигается критически высокое значение вязкости (1).

Заключение

Таким образом, стеклование жидкостей и аморфных полимеров объясняется замораживанием подвижности делокализованных возбужденных кинетических единиц – квантовых осцилляторов, обеспечивающих температуру стеклования, вязкое течение и лабильность структуры стеклообразующих расплавов. Полученные результаты подтверждают представление о том, что температура аморфных полимеров совпадает с температурой стеклования квантового «замораживания» вибрационной динамики макромолекул [2].