Интерпретация результатов количественного генетического анализа на основе аппроксимации кинетической кривой полимеразной цепной реакции в реальном времени

Количественный генетический анализ, проводимый методом полимеразной цепной реакции в реальном времени (ПЦР-РВ), основывается на выявлении положения характерной точки кинетической кривой — порогового цикла. Наиболее часто в качестве порогового цикла используют либо временнóе положение точки перегиба кинетической кривой, либо временнóе положение точки пересечения касательной к кинетической кривой, проведенной в точке перегиба с горизонтальной прямой, задающей характерный уровень сигнала. Характерным уровнем может быть фоновый сигнал или нижняя граница сигнала, практически достоверно отличающегося от уровня фона. Возможны и другие варианты.

Одной из задач работы является проверка возможности замены анализа непосредственно экспериментальных данных (кинетической кривой) на анализ аппроксимирующей зависимости и обоснованности применения в качестве последней функции логистического роста первого порядка. Выбор данной функции связан с тем, что она, во-первых, априорно удовлетворяет качественному виду кинетической кривой (относится к семей- ству сигмоидных функций) и, во-вторых, все ее три параметра имеют понятную содержательную интерпретацию.

Основным оцениваемым параметром аппроксимирующей зависимости является временнóе положение ее точки перегиба, что необходимо для определения порогового цикла при использовании обоих вышеописанных алгоритмов.

Второй задачей является выявление значимости влияния материала чипа — поликарбоната или полипропилена — на протекание ПЦР и на оценку положения порогового цикла применительно к различным анализируемым пробам, полученным путем различного разбавления исходной пробы. При этом данная задача решалась как для случая применения первого, так и для применения второго алгоритма поиска порогового цикла.

Третья задача связана с выявлением наличия разладки в последовательности измерений, одной из причин которой являлось наличие пузырей в реакционной камере на протяжении нескольких, преимущественно от 3 до 7, циклов ПЦР. Выявление критериев присутствия пузырей, исходя из формы кинетической кривой, является практически важной задачей. Ее решение позволит сделать вывод о допустимости использования полученных оценок положения порогового цикла и, как следствие, оценить правильность результатов количественного анализа.

Предложенные и обсужденные далее критерии можно отнести к двум группам. Первая группа критериев базировалась на определении параметров аппроксимирующей функции, вторая — на оценке характеристик погрешностей аппроксимации.

УСЛОВИЯ ЭКСПЕРИМЕНТА

Были изготовлены микрочипы из поликарбоната Novattro (SafPlast, Россия) и полипропилена PP 4445S (ТУ 20.16.51-136-05766801-2015, ПАО Нижнекамскнефтехим, Россия) методом термопрессования в гидравлическом прессе MM-100 (MTDI, Корея) на мастер-форме из нержавеющей стали, изготовленной методом лазерной микрообработки. Для герметизации структур использовались "Пленки для ПЦР плашек полимерные" Р-500 (ООО "ПКФ Современные технологии"). Топология микрочипов представляет из себя 3 камеры с подводящими каналами (рис. 1) [1].

На микрочипах проведена ПЦР-РВ по обнаружению ДНК сои, выделенной вручную с использованием набора реагентов М-сорб-ООМ для выделения ДНК и РНК из клинических образцов и объектов окружающей среды. Постановка реакции проводилась для исходной концентрации выделенных нуклеиновых кислот, для разведений на 1, 2 и 3 порядка и для положительного контрольного образца используемого набора "Расте-

Рис. 1. Изображение микрочипов.

Верхний — из полипропилена, нижний — из поликарбоната ние универсал" в трех повторах для каждого варианта. При работе с данным набором детектирование мишени проводится по красителю R6G, внутреннего положительного контроля — по Cy5. Все реагенты предоставлены ООО "Синтол" (Москва). Для сравнения аналогичные измерения проведены в пробирках на АНК-48 (ИАП РАН, СПб).

Измерения в микрочипах проводились на специально созданном макете, обеспечивающем режим термоциклирования для проведения ПЦР-РВ, возбуждение на длинах волн 530, 570 и 685 нм, регистрацию на 580, 630 и 660 нм соответственно. Зона детектирования представляла собой круг диаметром 3 мм. Камеры микрочипов заполнялись реакционной смесью с добавлением пробы ДНК, входы/выходы герметизировались ПЦР-пленкой. Микрочип размещался на нагревательном элементе пленкой вниз.

Одним из существенных недостатков при постановке ПЦР в камере чипа по сравнению с пробирками является образование пузырьков газа при термоциклировании. Оно не оказывает заметного влияния на протекание реакции, однако препятствует проведению корректного оптического детектирования.

АНАЛИЗ КИНЕТИЧЕСКИХ КРИВЫХ ПЦР

Определение положения порогового цикла выполняется на основе поиска точки перегиба кривой ПЦР. Используется аппроксимирующая зависимость логистического роста первого порядка:

a

У =-----7--------v

1 + exp ( - k ( x - x 0 ) )

Здесь а — максимальный сигнал (сигнал насыщения); k — коэффициент, определяющий скорость увеличения сигнала, связанный с эффективностью ПЦР; х 0 — точка перегиба кривой логистического роста первого порядка. Очевидно, что для нормированного сигнала параметр а должен быть близок к 1.

Значимость зависимости положения порогового цикла от материала микрочипа — поликарбоната (pc) и полипропилена (рр) — определяется известными статистическими методами.

• 1.    Обобщенный критерий Стьюдента позволяет дать оценку однородности положения порогового цикла для двух выборок, соответствующих различным материалам.

• 2.    Степень влияния материала на положение порогового цикла также выявляется с помощью однофакторного дисперсионного анализа.

Объемы выборок (число повторений экспериментов) малы (как правило, 3 повтора).

Метод одно- или многофакторного анализа хорошо известен [2]. Однако его используют до сих пор, в том числе и в различных прикладных задачах, например, см. [3, 4]. Поскольку даже двухфакторный анализ мы не использовали, то под термином "факторный анализ" полагаем однофакторный анализ. Расчетные формулы и необходимые критерии обсуждаются в [2].

Обозначения пробы : материал полимера определяет буквенную часть — pc или pp, цифра 1, 2 или 3 задает степень разбавления исходной пробы на 1, 2 или 3 порядка, т.е. в 10, 100 или 1000 раз соответственно (символ с на месте цифры — неразбавленная проба).

Проба vpk, или ВПК, представляет собой внутренний положительный контроль. Положение порогового цикла, смещенное более чем на 7 циклов по отношению к пороговому циклу данной пробы, свидетельствует об отсутствии анализируемого генетического материала. В табл. 1 представлены результаты определения положения порогового цикла в пробе внутреннего положительного контроля.

Динамика оценок порогового цикла при использовании различных наборов измерений сигнала пробы внутреннего положительного контроля иллюстрируется данными табл. 2. Оценка положения порогового цикла при использовании всей выборки 28.15 ±0.04 цикла.

Практически все оценки положения порогового цикла, за исключением сделанных по отсчетам 1– 25, имеют приемлемую точность с отклонением средней оценки в пределах нескольких сотых цикла. Принципиально важным является попадание точки перегиба кривой в диапазон выбранных отсчетов сигнала.

Диапазон 1–30 содержит лишь 2 измерения после точки перегиба, и точность оценивания ниже. В остальных случаях оценки положения точки перегиба сопоставимы по точности. Оценка точки перегиба осуществлялась по аппроксимирующей кривой логистического роста первого порядка во всех случаях. При этом при всех вариантах расчета, кроме первых двух, точка перегиба кинетической кривой являлась внутренней точкой, удаленной от границ временнóго интервала (цикл 1, цикл 40) по крайне мере на 20%-ю часть от длины интервала. Для интервала 1–35 положение порогового цикла 28.09 отстоит от верхней границы примерно на 7 циклов при полной ширине интервала 34 цикла.

Далее в табл. 3 представлены данные расположения точки перегиба кинетической кривой для исходной пробы, разбавленной на 1 порядок (в 10 раз), при использовании микрофлюидных чипов из различных полимерных материалов.

Табл. 1. Расчетные данные по положению порогового цикла

№ п/п	Pc_vpk	Pp_vpk
1	28.15 ±0.04	27.68 ±0.05
2	28.15 ±0.04	28.19 ±0.04
3	28.24 ±0.04	28.54 ±0.03
Среднее	28.18	28.14

Табл. 2. Оценки положения порогового цикла в зависимости от выбора отсчетов информативного сигнала

Диапазон отсчетов	Пороговый цикл	Диапазон отсчетов	Пороговый цикл
1–25	45.66	1–40	28.10 ±0.04
1–30	28.28 ±0.24	5–40	28.10 ±0.04
1–35	28.09 ±0.06	10–40	28.10 ±0.04
1–50	28.15 ±0.04	15–40	28.10 ±0.03

Табл. 3. Оценки положения точки перегиба кинетической кривой при использовании устройств из различных полимерных материалов

№ п/п	Pc_1	Pp_1
1	25.40 ±0.04	25.42 ±0.02
2	25.55 ±0.04	25.31 ±0.12
3	25.52 ±0.03	26.18 ±0.02
Среднее	25.49	25.64

Табл. 4. Положения точек перегиба кинетических кривых для разных разведений пробы

№ п/п	Pc_с	Pp_с
1	22.00 ±0.03	22.02 ±0.05
2	21.88 ±0.03	22.02 ±0.15
Среднее	21.94	22.02
№ п/п	Pc_2	Pp_2
1	28.22 ±0.04	30.31 ±0.48
2	28.61 ±0.04	29.20 ±0.36
3	28.15 ±0.04	29.97 ±0.11
Среднее	28.33	29.83*
№ п/п	Pc_3	Pp_3
1	31.48 ±0.06	31.12 ±0.03
2	31.71 ±0.03	31.36 ±0.03
3	—	31.75 ±0.04
Среднее	31.59	31.41

Примечание: *недостоверно из-за наличия пузырей (экспертная оценка).

Положение порогового цикла полагаем совпадающим с координатой точки перегиба кинетической кривой. Мы искали точку перегиба аппроксимирующей зависимости (1). Использование процедуры однофакторного дисперсионного анализа позволяет вычислить характерное значение случайной величины F — отношение двух дисперсий, связанных с расхождением средних оценок и дисперсией измерений внутри выборки, соответствующей каждому фактору, удовлетворяющей распределению Фишера с 1 и 4 степенями свободы, исходя из двух градаций фактора (два полимера) и суммарного числа 6 измерений. Этой величине F , примерно равной 0.291, соответствует доверительная вероятность 60%. Это значит, что с такой вероятностью расхождение элементов выборок (значений оценок порогового цикла) не может объясняться влиянием полимера.

Схожие результаты с вероятностями порядка 50% наблюдаются и для оценок порогового цикла при разбавлениях на 3 порядка ( F около 0.534). В табл. 4 приведены данные положений точек перегиба кинетических кривых, соответствующих другим разведениям исходной пробы.

Вышеуказанные значения также, в соответствии с методикой однофакторного дисперсионного анализа, свидетельствуют о независимости положения порогового цикла от выбора материала при заданном разведении пробы. Правда, уровень значимости не превышает 50%. Сопоставление положений порогового цикла для проб с разбавлением на 2 порядка не проводилось, поскольку на полипропиленовых чипах были выявлены пузыри.

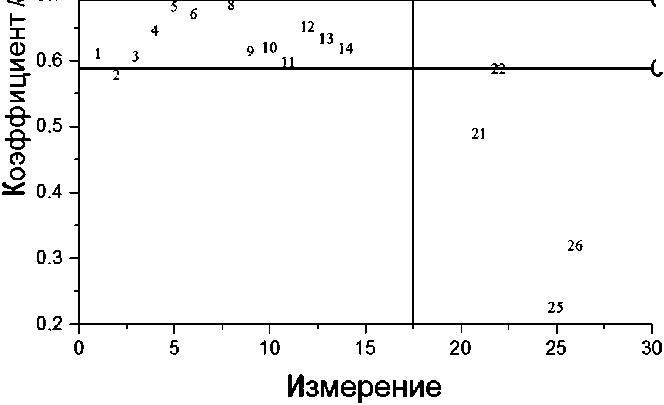
Далее на рис. 2 и 3 проиллюстрировано распределение параметров аппроксимации a и k применительно к различным кинетическим кривым ПЦР-РВ.

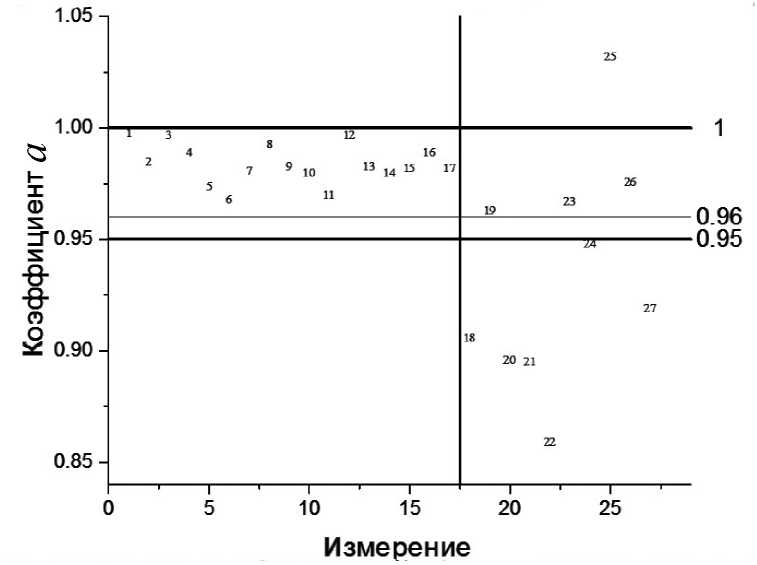
Рис. 2. Распределение оценок параметра а зависимости (1)

0.9 -|

23 24

0.8-

0.7

15 16

_____12

0.588

Рис. 3. Зависимость распределения параметра k модели (1)

0.693

Изначально сигнал нормирован и приведен к диапазону [0;1]. Нулю соответствует наименьшая величина сигнала, единице — наибольшая.

Таким образом, границы диапазона определяются по локальным минимумам и максимумам сигнала без его предварительной обработки.

ФОРМИРОВАНИЕ И ОБСУЖДЕНИЕ КРИТЕРИЕВ НАЛИЧИЯ ПУЗЫРЕЙ

В РЕАКЦИОННОЙ КАМЕРЕ

Очевидно, что наличие пузыря влияет на форму кинетической кривой. Изменение формы сигнала или/и скачкообразное изменение его параметров при сохранении вида зависимости относятся к двум типам разладки в последовательности измерений. Выявление разладки основывается либо на оценке параметров аппроксимирующей зависимости (1) с учетом их физического смысла (роли), либо на оценке погрешности аппроксимации. При этом принято допущение, что собственно погрешность аппроксимации пренебрежимо мала, а после компенсации аппроксимирующей детерминированной составляющей информативного сигнала погрешность носит случайный характер. Тогда эта погрешность анализируется на нали-чие/отсутствие детерминированных составляющих (трендов).

Предложенные и обсужденные далее критерии отсутствия пузырей и, как следствие, доверия к полученным результатам анализа основываются на попадании параметров детерминированной зависимости (1) в диапазон, соответствующий физически обоснованным значениям. В то же время группа критериев, связанная с оценкой параметров помехи, базируется на статистических оценках выборки с отсутствием трендов.

В настоящий момент наличие пузыря и его влияние на форму и параметры кинетической кривой требует исключения соответствующего результата анализа как недостоверного. Во многих случаях степень искажения теоретически обоснованной формы сигнала пробы как сигмоидной функции определяется исключительно на основе субъективной оценки.

Согласно экспертным оценкам, измерения 1–17 соответствуют отсутствию пузырей, 18–27 — наличие пузыря(ей).

На графике (рис. 2) выделена горизонтальная область допустимых значений параметра а при максимальном уровне нормированного сигнала 1. Теоретически оценка этого параметра должна совпадать с максимумом сигнала, он же уровень насыщения.

Жирными горизонтальными прямыми выделена область 0.95–1, в которой может находиться оценка параметра а при достаточно большом отношении сигнал/шум.

Отношение сигнал/шум для рассматриваемых нормированных сигналов пробы при условии корректной компенсации фонового сигнала и отсутствии статистических выбросов находится в диапазоне (50–60) к 1. При этом в качестве характерного значения сигнала рассматривается его среднее значение, примерно равное 0.5, а в качестве масштаба шума берется среднеквадратичное отклонение погрешности аппроксимации.

Первые 17 измерений, характеризующиеся отсутствием пузырей, полностью попадают в указанную область. При этом из 10 измерений с присутствием пузырей в данный интервал попадает лишь 3 значения из 10. Аналогичные результаты будут получены при повышении нижней границы области допустимых значений параметра а до значения 0.96.

Связь между средней эффективностью ПЦР Е и параметром уравнения k имеет вид:

E = exp( k ) - 1.

Поскольку теоретически обоснованное значение эффективности ПЦР не может превышать 1 (или 100%), то ожидаемое значение параметра k в аппроксимирующем уравнении не должно превышать 0.693.

На рис. 3 горизонтальные прямые соответствуют теоретически обоснованным значениям средней эффективности ПЦР 80% (нижняя прямая со значением 0.588) и 100% (верхняя прямая со значением 0.693). Из 17 измерений при отсутствии пузырей 12 достоверно попадают в указанную область, 5 находятся вне ее (2 из этих 5 измерений практически позиционируются на границе допустимых значений). При этом из 10 измерений с пузырями в данном диапазоне нет ни одного результата (1 практически попадает на границу, а остальные 9 достоверно вне области).

Комбинация этих ограничений позволяет выявить подозрительные с точки зрения наличия пузырей экспериментальные данные.

В некоторых алгоритмах параметр модели (1) х 0 — абсцисса точки перегиба определяет положение порогового цикла. Другим алгоритмом определения порогового цикла является поиск абсциссы точки пересечения касательной, проведенной в точке перегиба ПЦР-кривой, с осью ординат.

Если в аппроксимации (1) параметр a близок 1, то при использовании второго алгоритма положение порогового цикла смещено относительно х 0 и примерно равно x 0 - 2 / k .

Другие методы поиска параметров зависимости (1) используют не всю выборку (данные по всем циклам 1–40 или 1–50 циклам), а только набор отдельных элементов. Например, ранее в работе [5] была предложена оценочная формула для величины С = 1 + E= exp( k ) . Однако очевидно, что предложенная в этой работе четырехточечная формула, использующая измерения сигнала в двух парах равноотстоящих друг от друга отсчетах, условно нумерованных как

• n , n + k , n + m и n + m + k ,

  

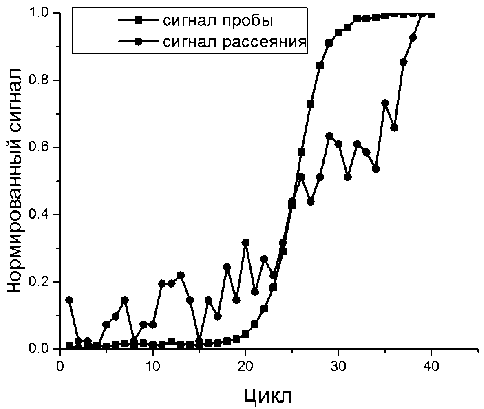
  Рис. 4. Нормированные сигналы пробы и рассеяния при отсутствии пузырей (из группы рс_1)

  
  
  

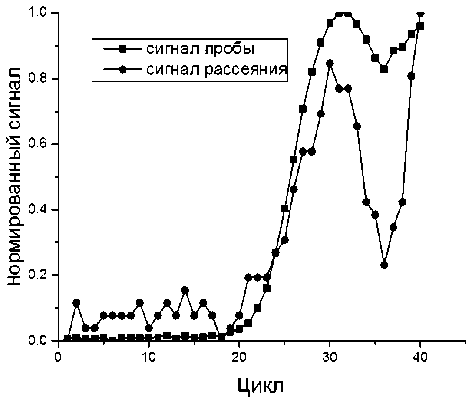
  Рис. 5. Нормированные сигналы пробы и рассеяния при наличии пузыря на заключительной стадии (рр_1)

  
  

заведомо дает более грубую оценку, чем аппроксимирующая зависимость, которая использует всю выборку измерений, как правило, 40–50.

Также оценка положения точки перегиба кривой может быть выполнена МНК при построении полинома 3-й степени, аналитического вычисления производной второго порядка, приравнивания ее к нулю и нахождения корня решением линейного уравнения. Этот прием был использован при поиске точки перегиба кривой плавления ДНК [6]. Подтверждена ожидаемая закономерность: более точные оценки получаются при использовании отсчетов с линейного участка кривой со значениями нормированного сигнала, близкими к 0.5. При этом лучше брать не ровно 4 точки, а объем выборки должен иметь несколько степеней свободы (не менее 6–8 отсчетов).

Например, для кинетической кривой оценка точки перегиба 25.55 (см. табл. 3, строку 2). Поли- номиальная аппроксимация кубической параболой по отсчетам 22–27 дает оценку точки перегиба 25.79, что приемлемо для примерного расчета. Здесь приведены типичные зависимости нормированных сигналов пробы и рассеяния при отсутствии пузырей (рис. 4) и при наличии одного пузыря (рис. 5).

Кривая, соответствующая нормированному сигналу рассеяния (см. рис. 4 и 5), может быть адекватно аппроксимирована полиномом второй степени.

Положение порогового цикла, как указано ранее, может определяться с помощью двух алгоритмов. Для исходной пробы, разбавленной в 10 раз (на 1 порядок), в табл. 5 приведены данные оценок положения порогового цикла при анализе на чипах из различных полимерных материалов.

Табл. 5. Расчетные данные по положению порогового цикла в зависимости от метода его поиска

№ п/п	Точка перегиба		Касательная
	Pc_1	Pp_1	Pс_1	Pp_1
1	25.40	25.42	22.13	22.36
2	25.55	25.31	22.09	22.57
3	25.52	26.18	22.23	22.75
среднее	25.49	25.64	22.15	22.56

Данные табл. 5 свидетельствуют о том, что при оценке положения порогового цикла с использованием построения касательной к кинетической кривой в точке перегиба на основе однофакторного анализа получаем отношение приведенных дисперсий F примерно 11.65. Вывод: с вероятностью 97% различие положений порогового цикла при использовании точки пересечения касательной к перегибу кривой и оси ординат объясняется именно различием материала (поликарбонат или полипропилен). Для алгоритма поиска порогового цикла непосредственно в точке перегиба вывод противоположен: с большой вероятностью фактор выбора материала на положение порогового цикла не влияет.

Другая группа алгоритмов выявления присутствия пузыря может основываться на статистическом критерии восходящих и нисходящих серий погрешности аппроксимации сигналов пробы или рассеяния при достижении высокой достоверности детерминации (коэффициент детерминации заведомо должен превышать 0.9). Один из таких критериев имеет значимость 5% и требует удовлетворения числом восходящих и нисходящих серий двух условий. При общем числе отсчетов (погрешностей аппроксимации), равном N :

ser ( N ) >

2 N -1 ,     /16 N - 29

--1.96. ------------ 3             90

T max ( N ) <  T (N) ,

т ( N ) = <

N <  26,

26 <  N <  153,

153 <  N <  1170

Формула (2) базируется на данных [7, c. 486– 488 ], а ограничения (3) обсуждаются в [8]. Применительно к оценкам информативного сигнала (сигнал пробы) на рис. 4 и 5 объем исходных выборок был 40 отсчетов. Так как для оценки наличия восходящей или нисходящей серий требовалось построить правую разность первого порядка, то объем рассматриваемой выборки разностной погрешности N равен 39. Соответственно, восходящая серия содержит последовательность положительных значений разностной погрешности, нисходящая — отрицательные. Согласно первому условию (2), число серий ser ( N ) должно быть более 20, согласно второму условию (3), наибольшая длина серии должна быть строго меньше 6, т.е. не более 5.

Наблюдаются следующие тенденции: кривой пробы на рис. 4 соответствует число серий 23 и максимальная длина серии 4. Таким образом, оба условия (2) и (3) выполнены. Применительно к кривой пробы рис. 5: число серий 19, максимальная длина серии 5. Условие (2) нарушено, условие (3) выполнено.

Аналогичные данные по кривым рассеяния после компенсации детерминированной составляющей — полинома второй степени применительно к рис. 4: число серий 29, максимальная по длине серия 3; применительно к рис. 5: число серий 19, максимальная по длине серия 6.

Если в первом случае (рис. 4) оба условия также выполнены, а это случай отсутствия пузырей, то во втором случае (рис. 5) нарушены оба условия.

Ответ на вопрос, насколько данные критерии присутствия пузырей универсальны, может явиться предметом дальнейшего исследования на основе более репрезентативной статистики. Еще один из критериев можно связать с анализом распределения восходящих или нисходящих фаз (серий) по длине и с расхождением с теоретическими оценками математического ожидания числа серий заданной длины при отсутствии в выборке трендов.

Математическое ожидание числа серий длины d ( d = 1, 2, 3, …) [7] представлено далее формулой (4):

N d =

2( N - d - 2)( d² + 3 d + 1) ( d + 3)!

При числе отсчетов 39 математические ожидания числа восходящих или нисходящих серий длин 1, 2, …, 5 равны соответственно 15.00, 6.42, 1.79, 0.38 и 0.07.

Близость реального распределения серий к теоретически обоснованному оценивается с использованием критерия согласия Пирсона (или Хи-квадрат) со следующими поправками и допущениями: а) рассматриваются только три значения — числа серий длины 1, длины 2 и длины 3 или более; б) найденной величине присваивается число степеней свободы 2.5, если она равна 6.3 или более, либо 2 степени свободы при меньших значениях характеристики расхождения. Во втором случае вводится уменьшающий поправочный коэффициент 6/7. Эта классическая методика сформулирована в работе [9]. Особенности распределений фаз по длинам для случаев наличия или отсутствия пузырей иллюстрируются в табл. 6.

Соответственно рассматриваются процентная точка распределения Хи-квадрат с 2 степенями свободы и ее процентные точки [10].

Если уровень вероятности согласия с гипотезой менее 10%, то ее следует отвергать. Следовательно,

Табл. 6. Распределение восходящих и нисходящих фаз по длинам для различных особенностей проведения ПЦР-РВ

Число фаз (серий)	Теория (4)	Проба, рис. 4	Рассеяние, рис. 4	Проба, рис. 5	Рассеяние, рис. 5
d = 1	15.00	12	22	10	9
d = 2	6.42	7	4	4	5
d = 3	1.79	3	3	1	2
d = 4	0.38	1	0	2	2
d = 5	0.07	0	0	2	0
d = 6	0.01	0	0	0	1
Хи-квадрат*		1.64	3.77	4.93	5.04
Вероятность**		44	16	9	8

Примечание: *введен поправочный коэффициент 6/7 [9], а данные по d = 3, 4, 5 и 6 просуммированы;

**вероятность округлена до целых процентов.

гипотеза об отсутствии трендов (разладок) после компенсации аппроксимирующей детерминированной составляющей сигнала при наличии пузырей (группа данных рис. 5) должна быть отвергнута. Указанная гипотеза применительно к информативному сигналу пробы при отсутствии пузырей принимается с высоким уровнем значимости (более 40%), что является достаточным для принятия гипотезы об отсутствии трендов в последовательности погрешностей аппроксимации и, как следствие, отсутствии разладки в последовательности исходных измерений.

Следовательно, предложенные алгоритмы принятия решений о наличии пузырей, как связанные с анализом информативного сигнала, так и с погрешностью аппроксимации, с большой вероятностью позволяют делать правильные выводы. Однако насколько полученные результаты специфичны по отношению к выбранному объекту анализа и в какой степени допускают обобщение на другие объекты, требует дополнительного исследования.

ЗАКЛЮЧЕНИЕ

Проведенные серии количественного генетического анализа на основе ПЦР-РВ с использованием полимерных чипов выявили следующие закономерности: при определении порогового цикла как точки перегиба кинетической кривой (логистическая кривая первого порядка) отсутствует значимая зависимость найденных величин от материала чипа (поликарбонат или полипропилен).

В то же время, если оценивать положение порогового цикла по абсциссе точки пересечения касательной к кинетической кривой, построенной в точке ее перегиба, с уровнем фонового (минимального) сигнала, с доверительной вероятностью более 90% фактор материала полимера на положение порогового цикла влияет.

Информативный сигнал (сигнал пробы) при отсутствии пузырей с высокой точностью аппроксимируется логистической кривой первого порядка — одним из типов сигмоидной кривой. При этом коэффициент детерминации превышает 0.99. Также в данных условиях при нормализации сигнала пробы отношение сигнал/шум достигает значений 55–60. Под масштабом (характерной величиной) сигнала понимается среднее значение, под масштабом шума — среднеквадратичное отклонение погрешности аппроксимации.

Проверка критериев наличия пузырей для нормированной кинетической кривой:

• а)    коэффициент а в аппроксимирующей зависимости существенно ниже 1;

• б)    нефизическое значение коэффициента k , достоверно превышающее значение 0.70 или существенно меньшее 0.58;

• в)    на основе анализа восходящих и нисходящих серий в последовательности измерений погрешностей аппроксимации наблюдается невыполнение одного или двух условий отсутствия трендов, а также существенное отклонение длин восходящих и нисходящих серий (фаз) от теоретически обоснованных при отсутствии трендов распределения.

Комбинация предложенных критериев после дополнительной проверки их универсальности (правомерности обобщения на другие биологические объекты или/и другие материалы чипа) может быть включена в программно-математическое обеспечение приборов, что в перспективе исключит участие субъективного фактора (эксперта) при принятии решения о присутствии пузырей в реакционной камере на какой-либо стадии построения кинетической кривой.

Работа выполнена в рамках Государственного задания Министерства науки и высшего образования Российской Федерации № 075-00761-22-00 (тема "Микрофлюидные устройства с интегрированными функциональными микро- и наноразмерными структурами для биологических и медицинских исследований", FFZM-2022-0012).