Интервальное оценивание объемов потребления газа населением региона с учетом сезонного фактора

зав. кафедрой филиал РГГУ в г. Калуге

Россия, г. Калуга

ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ ОБЪЕМОВ ПОТРЕБЛЕНИЯ ГАЗА НАСЕЛЕНИЕМ РЕГИОНА С УЧЕТОМ СЕЗОННОГО ФАКТОРА

В составлении экономических прогнозов огромное распространение получили формализованные методы прогнозирования, такие как методы экстраполяции и методы математического моделирования. Одним из распространенных методов экстраполяции является метод подбора функций, который заключается в подборе по фактическим данным формы зависимости, которая обеспечит наименьшие отклонения данных исходного ряда от соответствующих расчетных значений. Расчет параметров для конкретной функциональной зависимости может быть осуществлен методами конфлюентного анализа, которые при определении точечных оценок параметров позволяют учитывать погрешности, как в значениях функции, так и в значениях ее аргумента.

Кроме точечных оценок параметров функций необходимо находить интервальные оценки параметров и интервальные оценки функциональных зависимостей [1]. Для практики именно интервальные оценки представляют большую ценность, поскольку дают достаточное количество информации об оцениваемом параметре.

Рассмотрим потребление газа населением Калужской области G при изменении температуры воздуха t . Для оценивания параметров линейной зависимости G=a+bt воспользуемся моделью

G = a+b^ + ^

i = 1 ,n,

s

1 ti  - +S которая позволит учесть погрешности значений функции G – потребление газа и погрешности значений аргумента t – температуры.

Кроме точечных значений функции G определим доверительный интервал для линейной функции G = a + bt . Интервальная оценка функции G при заданной доверительной вероятности у имеет вид [2]:

P

[<€ - t y JDG

< G < G +1Y3d(G)} = Y,

где t _Y - квантиль распределения Стьюдента. Дисперсия D ( (€ ) определяется по формуле:

(^

D (<€) =я 2 + ( t - г ) 2    ^—_=а 2 1 + J t -HL .

Х      n           V'V — X2       n      (—х2

D t - ^{- 1} )          E ( t ^{- 1} )

=1                    V       -=1

В зависимости от периода времени года: холодный или теплый, разделим исходные данные на две группы точек, каждую группу точек аппроксимируем линейной зависимостью и по (1) определим доверительные интервалы функциональных зависимостей с заданной доверительной вероятностью у .

В результате аппроксимации каждой группы точек были получены следующие уравнения:

• <    = 98788 , 5 - 37771 - 1 ;                                            (2)

• < тепл = 126585 , 2 - 3643 , 5 - 1 .                                             (3)

На рисунках 1-2 показаны результаты аппроксимации каждой группы точек (сплошная линия) и интервальные оценки функциональных зависимостей с доверительной вероятностью у = 0,95 (пунктирные линии). При этом квантиль распределения Стьюдента для p = 2 и n = 10 принимался равным 1^ = 2,31. Вертикальные пунктирные линии на рисунках 1-2 соответствуют средним значениям температуры и отклонениям от средней температуры для каждого периода времени года.

Потребление

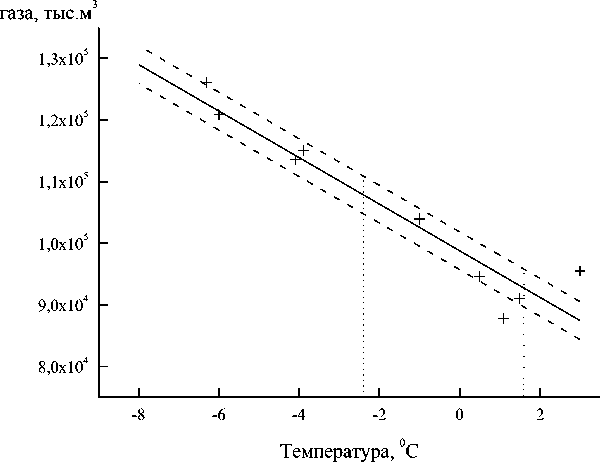
Рисунок 1 – Результаты обработки данных, соответствующих холодному периоду времени года с доверительной вероятностью у = 0,95

Потребление

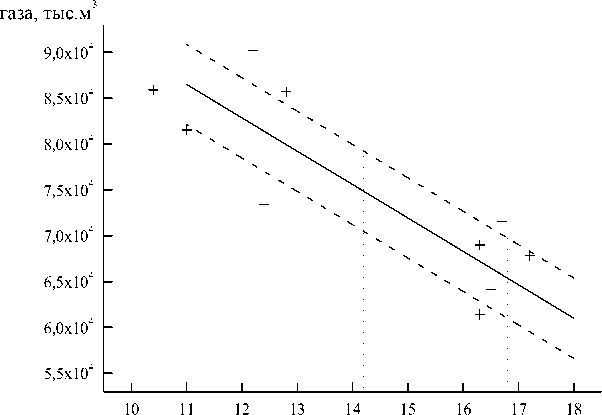
Температура, 0С

Рисунок 2 – Результаты обработки данных, соответствующих теплому периоду времени года с доверительной вероятностью у = 0,95

Проверим значимость уравнений (2)–(3). Совокупности данных, соответствующие холодному и теплому периоду времени года, содержат по 10 значений. При n = 10, p = 2 и уровне значимости а = 0,01 критическое значение F_Kp ( 0,01;1;8 ) = 11,26. Для уравнения (2), соответствующего холодному периоду времени года, Р_набл = 120,02. Для уравнения (3), соответствующего теплому периоду времени года, Р_набл = 23,41. Для данных, соответствующим холодному и теплому периоду времени года, условие F_Ha6п > F_Kp выполняется, поэтому уравнения (2) - (3) являются значимыми.

По уравнениям (2) – (3) для средней температуры воздуха, а также верхних и нижних значений диапазона температур, соответствующих предельным отклонениям t ± 3 ^ ( t ) , определим точечные и интервальные значения потребления газа населением для холодного и теплого периода времени года (таблицы 1-2).

Таблица 1 – Точечные и интервальные значения потребления газа населением, соответствующие средней температуре, верхним и нижним значениям диапазона температур для теплого периода времени года

Температура, ° С	Потребление газа населением, тыс.куб.м
	G H ( t )	G ( t )	G B ( t )
t = 22 ,1 0 С в	31089 , 6	45946 , 1	60802 , 6
t cp = 14 , 2 0 С	70544 , 4	74919 , 9	79295 , 3
t = 6 , 2 0 С н	89194 , 3	103893 , 6	118593

Таблица 2 – Точечные и интервальные значения потребления газа населением, соответствующие средней температуре, верхним и нижним значениям диапазона температур для холодного периода времени года

Температура, ° С	Потребление газа населением, тыс.куб.м
	GH ( t )	G ( t )	G B ( t )
t„ = 9 , 7 0 С в	51900 , 3	62109 , 6	72319
t cp =- 2 , 4 0 С	104979 , 6	108042 , 4	111105 , 2
t =- 14 , 6 0 С н	143783 , 6	153975 , 3	164166 , 9

Определение не только точечных, но и интервальных оценок прогнозируемых показателей с учетом сезонного фактора повышает достоверность прогноза и, как следствие, снижает степень неопределенности и риски хозяйствующего субъекта, и повышает эффективность принимаемых управленческих решений.

Исследования проведены при финансовой поддержке Российского гуманитарного научного фонда и правительства Калужской области (проект № 12-12-40022 а(р)).