Интервальные характеристики групповых пуассоновских моделей трафика телекоммуникационных систем

Появление сетей передачи данных с коммутацией пакетов показало, что пуассоновские модели потоков не являются адекватными, и потребовало разработки новых моделей, основанных на непуассоновских распределениях. Исследуются потоки с распределениями Вейбулла, Эрланга, Парето, гамма-распределениями и др. Все интервалы времени, представляемые данными распределениями вероятностей, по-прежнему считались взаимно независимыми. Это позволяло применить хорошо разработанный аппарат теории очередей для анализа сетей с пакетной коммутацией. Описание сложных коррелированных потоков в современных телекоммуникационных сетях часто производилось с использованием «фрактальных» процессов. Сотни работ посвящены анализу «самоподобного» трафика. Однако ощутимых практических результатов указанные исследования не дали.

Недостаточная эффективность представления трафика моделями «самоподобных» процессов привела к созданию целого класса моделей потоков, управляемых цепью Маркова. Этапы разви- тия указанных моделей представлены в обзоре [1]. В нашей стране они были названы МС-потоками, а в США эволюционировали от «разносторонних (versatile) потоков», через «Ν-потоки (потоки Ньютса) [2] до марковских входных потоков (MAP ‒ Markovian Arival Process) и их обобщения ‒ групповых марковских входных потоков (BMAP ‒ Batch Markovian Arival Process) [6‒13].

Стимулом к развитию ВМАР-моделей явились их матричные представления, предложенные в работах М. Ньютса. Переход к матричным представлениям вероятностных характеристик ВМАР-потоков позволил осуществлять описание их работы и открыл широкий простор для аналитических исследований. Однако определение характеристик входного потока заявок часто осуществлялось отдельно от характеристик обрабатывающей его системы. Вместе с тем такая характеристика, как время обработки пакета в телекоммуникационных системах, зависит не только от пропускной способности системы, но и тесно связана с размером пакета, который является одной из характеристик входного потока. Наиболее значительной работой в области анализа систем массового обслуживания (СМО) с подоб- ными потоками, по-видимому, можно считать [3]. Одним из перспективных, на наш взгляд, направлений изучения пакетного трафика является разрабатываемый нами интервальный метод [4], позволяющий заменить анализ интервалов времени между соседними заявками и интервалов времени обработки заявок, анализом одной случайной величины ‒ числом заявок, поступающих в течение последовательных интервалов времени обработки каждой из заявок. Показано, что дисперсия и корреляционные свойства указанной случайной величины при заданной загрузке полностью характеризуют средний размер очереди в СМО [4].

Для одноканальных СМО было получено соотношение (1), обобщающее известную формулу Хинчина ‒ Поллачека для среднего значения очереди q(р) и справедливое для любых стационарных потоков заявок при заданном коэффициенте загрузки р:

-(-) = Dm (р) + 2 Cov [ q,—1 (р); mi (Р)] -Р qР>            2(1 -р)            2

_ mE(р) р

= 2(1 -р ) — 2'

Анализ числителя mE ( р ) формулы (1) показывает, что среднее значение очереди для потоков любого вида зависит от двух составляющих: первая составляющая - это дисперсия D m ( р ) числа заявок (пакетов) m i ( р ), поступающих в течение интервала времени обработки одной заявки, а вторая ‒ это составляющая, обусловленная наличием корреляционных связей в указанном потоке. Корреляционные связи учитываются ковариацией Cov [ q. 1( р ); m. ( р )] между значениями m i ( р ) и значениями очереди q i - 1 ( р ) на предыдущем интервале анализа.

В частном случае для пуассоновского потока указанная составляющая равна нулю, а дисперсия D m ( р ) = р . Тогда при постоянном времени обслуживания обобщенная формула (1) приобретает обычный вид:

q ( р ) = —^р— 2(1 -р )

.

Групповой неординарный пуассоновский поток

Одной из разновидностей ВМАР-потоков является неординарный пуассоновский поток событий. В таком потоке выполняются свойства стационарности и отсутствия последействия, но не выполняется свойство ординарности. Рассмотрим пуассоновский поток независимых событий с параметром Х. Каждое событие заключается в одновременном появлении в момент tk «пачки» из µk независимых случайно распределенных чисел заявок с распределением P |цk = k| = fk. Τакой поток называют пуассоновским неординарным (групповым) потоком независимых событий, и он рассмотрен в [5].

Примем, что τ ‒ это интервал времени обработки одной заявки. Разделим достаточно большой промежуток времени Т , в течение которого действует поток указанных событий, ʜa N _τ таких последовательных интервалов. Пусть m i ( т ) - число событий, произошедших в течение i -го интервала времени т . Тогда вероятности наступления на интервале τ ровно n событий подчиняются закону Пуассона:

P\mi (т) = n\ = Pn (Хт) = (^т) e'".

n!

Каждому из событий сопутствует появление «пачки» с распределением вероятностей чисел заявок fk. Введем производящую функцию ∞ f (z) = Zfkzk. Поскольку все цk взаимно неза-k=0

висимы и одинаково распределены, появлению на интервале т ровно m i ( т ) заявок при условии, что на указанном интервале произошло n событий, соответствуют вероятность ( f_k ) " ипроизво-дящая функция [ f ( z )] n .

Производящая функция G_{m ( т )} ( z ) числа заявок на интервале τ есть

∞

Gm(т)(z) = Z P (Хт)[ f (z)]n = n=0

= Z (Xr£ e _XT [ f (z)] n = n=0 n!

= [ Z ( Хт f ( z )) n. e -Хт f ( z ) ] e Хт [, f ( z ) - 1] = e Хт [. f ( z ) - 1] .

n = 0      n !

Определим среднее число заявок на т :

Г                     ^{d G} m ( т )^{( z} )

m (т) = >, m. (т) P1[ m. (т)] =----------

= 0                        ∂ ^z

= Хт f ¹ ( z ) e ^^[- ^{f ( z ) - 1]}|     =Хт f ¹ (1).

z = 1

Учитывая, что ∞∞

f1 (1) = d;- Z fkzk   =Z kfk = k, dz k=0       z=1 k=0

получим m ( т ) = Хт k , где k - среднее число заявок в «пачке». Определим второй начальный момент:

∞

m (т)2 = Z mi2 (т) P2 [ mi (т)] =

= 0

m (т)\ 7

z = 1

= Xtf1 (z) eX2[ f(2 )-1]|    = z=1

= [Xtf11 (z) + (Xtf1 (z ))2 ] eX2[ f(2 )-1]|    = z=1

= Xt k ² + ( Xt k ) ² = Xt k ² + m f ) ² .

Определим дисперсию D m ( t ) числа заявок на интервалах t :

D m ( t ) = m ( t ) ² - m ( t ) ² = Xt k ² = = Xt ( D_k + k ²) = p k (1 + v k ),

где p = Xt k = m ( t ) - общий коэффициент загрузки;

ν

2 k

D k

( k ) ²

‒ квадрат коэффициента вариации чи- сел заявок в пачках. Дисперсия Dm (р) линейно зависит от коэффициента загрузки р. Преобразуем формулу (1):

q p = DJ ) -р , 2(1 -р )    2

где J(р) = 1 + 2rq 1 m (р) называют ковариационным индексом дисперсии, а rq m (р) = qi-1 i

Cov [ q . - i ( р ); m , ( р )]

D m ( р )

‒ нормированная ковариационная функция.

В дальнейшем с помощью имитационного моделирования мы покажем, что при малых коэффициентах загрузки значение индекса дисперсии для потоков с пуассоновским распределением чисел заявок в пачках мало отличается от едини- цы и корреляционная составляющая практически отсутствует. При этом формула (1) упрощается mE(р) = Dm (р) = рE и q(p) = АМ_£ = _PE_-£,

2(1 -р ) 2 2(1 -р ) 2

где E = k (1 + v k ). Дисперсия D m ( р ) в (5) линейно зависит от коэффициента загрузки р , а ее значение пропорционально среднему числу заявок в пачке.

Рассмотрим частные случаи.

• 1.    Ординарный пуассоновский поток: k , = 1, k = 1, v k = 0, E = 1 - при этом справедлива формула (2).

• 2.    Все пачки имеют одинаковое число заявок: k = k , v k = 0, E = k .

• 3.    Числа заявок в пачках распределены по за

• 4.    Числа заявок в пачках целые и распределены по экспоненциальному закону: k = k , v 2 = 1, E = 2 k .

кону Пуассона: k = k , v k = —, E = k + 1. k

Групповые неординарные пуассоновские потоки с зависимым числом заявок в пакете

Мы рассмотрели групповые пуассоновские потоки, в которых случайные, взаимно независимые числа заявок µ _k в пачках не зависят также и от интервалов времени между соседними событиями (соседними пачками). Рассмотрим теперь поток, в котором указанные числа заявок в пачках пропорциональны длительностям интервалов врем е ни ϑ _k = t_{k + 1} - t_k межд у со с едними пачками ц _k = k X3 _k . Очевидно, что ц _k = k . Поскольку интервалы ϑ _k между соседними пачками взаимно независимы и имеют экспоненциальное распределение, числа заявок µ _k в пачках также взаимно независимы и имеют экспоненциальное распределение со средним значением k , параметрами v k = 1 и E = 2 k .

Однако, в отличие от рассмотренного выше примера, числа заявок в каждой из пачек пропорциональны длительностям соответствующих интервалов 3 _k , и очередь, возникающая с появлением каждой пачки, успевает завершиться до появления следующей пачки заявок, причем даже при коэффициенте загрузки, равном единице.

Покажем это, принимая во внимание, что µ _k τ = k λτϑ _k = ρϑ _k ‒ длительность времени обработки всех заявок на интервале 3 _k . Обозначим через A _k = 3 _k - р3 _k = 3 _k (1 - р ) запас по времени обработки всех заявок на указанном интервале. Относительный запас по времени _ϑ ^k = 1 -ρ остается постоянным на всех интервалах и зависит только от коэффициента загрузки. При максимальной загрузке ρ= 1 запас равен нулю, но обработка всех заявок в очереди успевает завершиться до появления очередной пачки заявок (это хорошо иллюстрируют рисунки 7, 8 в разделе с результатами имитационного моделирования).

Даже в случае максимальной загрузки, когда на интервале, предшествующем интервалу появления пачки, происходит обработка последней заявки, очередь заявок q i - 1 ( р ) = 0, и, следовательно, q . - 1 ( р ) m i ( р ) = 0. Учитывая, что Cov [ q , - 1 ( р ); m , ( р )] = q , _ 1 ( р )[ m , ( р ) - р ], преобразуем формулу (1):

q ( р )(1 -р ) = D m ^ +

+ Cov [ q , - 1 ( р ); m , ( р )] - ^{р (1}2 ^{р )} =

= D m 2 p ) + q , - 1 ⁽ р ) m , ⁽ р ) ^- q ⁽ р ) р^{- р (1} ₂ ^{р )} ,  (6)

—~ = Dm (Р) Р(1 -Р) = EР-Р(1 -Р) qρ 22    2

q ⁽ р ) = k Р^{- Р (}12 ^{Р )} -

Максимальное значение дроби в полученном выражении не превышает 0.125, поэтому даже при небольших значениях чисел заявок в пачках характеристика q ( р ) практически линейна, как это будет видно из рисунка 9 в разделе имитационного моделирования.

Равенств о нулю математического ожидания q i - 1 ( р ) m i ( р ) = 0 свидетельствует, что для данного потока взаимная ковариация Cov [ q i - 1 ( р ); m i ( р )] не равна нулю и отрицательна:

Cov ^[ q - ⁽ р ); m ⁽ Р ^)] =

= q i - 1 ( р ) m ⁽ р ) ^- q ( р ) р = ^- q ( р ) р -

Подставляя значения q ( р ) из (6), получим: Cov ^[ q i - 1 ⁽ р ); m ⁽ р ^)] =

• = - k р 2 ,Р" Р > = — k р 2 (1 - 1 —Р ). ' 2 2 k

При достаточно больших значениях чисел заявок в пачках ковариация имеет практически квадратичную зависимость от коэффициента загрузки.

Соотношение (7) позволяет определить значения числителя в первой дроби (1), обозначенного нами в разделе моделирования на рисунке 9 через mE ( р ):

mE ( р ) = 2 k р (1 -р )(1 + Д). (8) 2 k

Указанная зависимость имеет максимум при значениях р~ 0,5 - см. рисунок 9. Именно наличие члена (1 -р ), сокращающегося при подстановке в формулу (1), приводит для данного потока к практически линейной зависимости среднего размера очереди от коэффициента загрузки, показанной в (6).

Групповые гиперпуассоновские потоки

Сумму независимых одновременно параллельно протекающих рассмотренных выше потоков назовем групповым гиперпуассоновским потоком. В отличие от большинства потоков, управляемых цепью Маркова, протекание всех суммируемых потоков происходит не последовательно, а непрерывно, параллельно во времени. При получении гиперпуассоновского потока происходит суммирование нескольких пуассоновских потоков событий, каждое из которых представляет пачку одновременно поступающих заявок. Однако суммарный поток событий (появлений пачек) является пуассоновским. Следовательно, суммарный поток заявок также является групповым пуассоновским потоком.

Линейная зависимость числителя в формуле (5) от коэффициента загрузки при малых загрузках существенно упрощает определение средних размеров очередей суммарного гиперпуассоновского потока при мультиплексировании взаимно независимых групповых пуассоновских потоков:

M

Р^=ЕРг j=1

M _ρ

E = "Z- E - j = 1 ρ Σ

С точки зрения средних значений образуемых очередей полученный суммарный гиперпуассоновский поток эквивалентен соответствующе- му групповому пуассоновскому потоку, однако характеристики их мгновенных значений могут существенно отличаться. В дальнейшем мы покажем, что соответствующим выбором характеристик суммируемых потоков можно получить суммарный гиперпуассоновский поток с характеристиками, весьма близкими к реальному моде- лируемому потоку.

Имитационное моделирование

В этом разделе подтвердим полученные выводы результатами имитационного моделирования с помощью разработанной нами программной системы АМС [4]. Система позволяет получить и исследовать основные интервальные характеристики потоков, представленных в формате .txt в виде последовательности моментов поступления заявок.

Групповой поток с пуассоновским распределением вероятностей независимых чисел заявок в пачке. Были сгенерированы два групповых пуассоновских потока с одинаковыми значениями интенсивностей λ= 1 заявка в секунду. Первый поток содержал пачки заявок, имеющих пуассоновское распределение чисел заявок в пачке, со средним значением k ₁ = 10 заявок в пачке и интенсивностью поступления пачек Х 1 = 0,1 пачка в секунду. X = к 1 X 1 = 1. Второй поток имел следующие характеристики:

X = X 2 = 1; k2 = к2 = 1, то есть каждая пачка состояла точно из одной заявки и, следовательно, второй поток был обычным пуассоновским потоком с интенсивностью, равной X.

Ηа рисунке 1 совмещены графики чисел заявок на интервалах обслуживания для первого и второго потоков при коэффициенте загрузки р = 0,1. Пуассоновский поток весьма равномерен

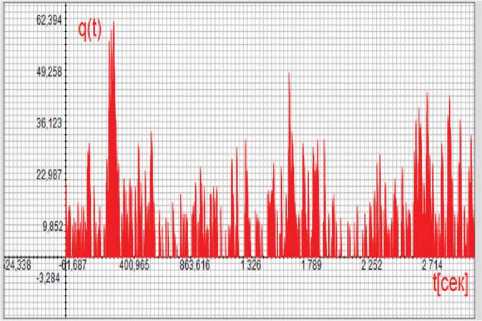
Рисунок 2. Очереди, возникающие при обслуживании группового пуассоновского потока в однолинейной

СМО при коэффициенте загрузки р = 0,5

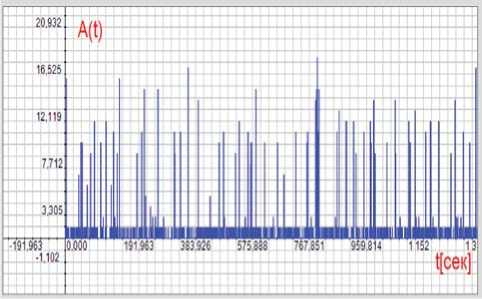
Рисунок 1. Числа заявок на интервалах обслуживания для первого и второго потоков при коэффициенте загрузки р = 0,1

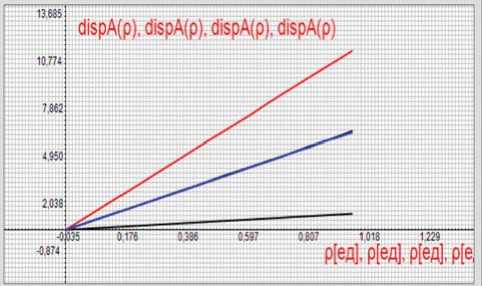
Рисунок 3. Зависимости дисперсии D m ( р ) чисел заявок на интервалах обслуживания от коэффициента загрузки

и в основном имеет не более одной заявки, в то время как групповой пачечный поток на аналогичном интервале имеет свыше 10 заявок, числа которых распределены по закону Пуассона. Пачечный характер группового потока приводит к возникновению больших очередей при его обслуживании.

На рисунке 2 показан график изменения очереди при обслуживании группового пуассоновского потока в однолинейной СМО при коэффициенте загрузки р = 0,5. Максимальные значения чисел заявок в очередях превышают 60, что является результатом высокой пачечности потока.

Наиболее значительной интервальной характеристикой рассматриваемых потоков является зависимость дисперсии D m ( р ) чисел заявок на интервалах обслуживания от коэффициента загрузки. Нами было показано, что указанная зависимость носит линейный характер и для пуассоновского распределения вероятностей чисел заявок в пачках определяется соотношением (3). При заданных параметрах группового потока:

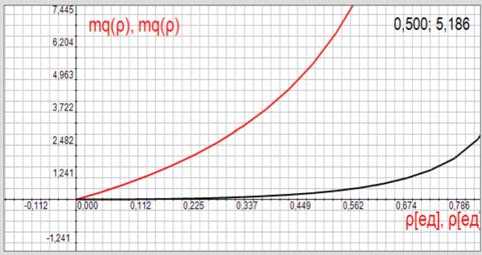
Рисунок 4. Зависимости средних размеров очередей q(р) от коэффициента загрузки v 2 = D =1 = 0,1; E = к (1 + v 2) = 11,

(к) к в то время как для обычного пуассоновского потока E = 1. Зависимости дисперсии Dm (р) чисел заявок на интервалах обслуживания от коэффициента загрузки, полученные в результате имитационного моделирования обоих потоков, отражены на рисунке 3. Верхний график соответствует групповому пуассоновскому потоку с углом наклона E = 11. Нижний график соответствует обычному пуассоновскому потоку с углом наклона E = 1.

Средний график соответствует потоку, полученному в результате суммирования указанных потоков. Видно, что все зависимости строго линейны. На рисунке 4 пок аза ны зависимости средних размеров очередей q ( р ) от коэффициента загрузки, полученные в результате имитационного моделирования обоих потоков.

Верхний график ‒ групповой поток, нижний график ‒ пуассоновский поток. В верхнем углу показано значение размера очереди для группового потока при коэффициенте загрузки р = 0,5, полученное непосредственно с графика, q ( р ) = 5,186. Теоретическое значение, определенное по формуле (4), q ( р ) = 5,25. Незначитель-

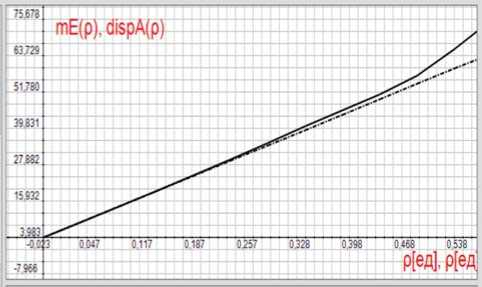
Рисунок 5. Изменение значений числителя

D m ( p ) J ( p ) и изменение значений дисперсии D m ( р )

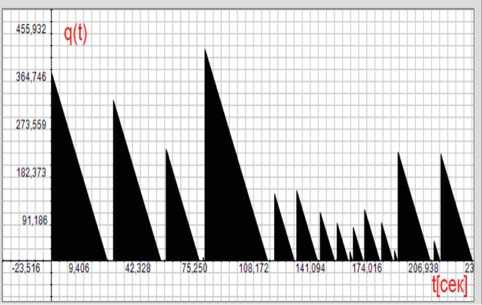
Рисунок 7. Изменение размеров очередей во времени для первого потока

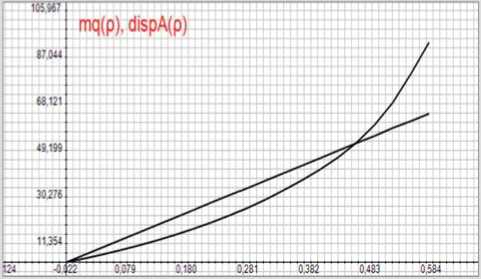
Рисунок 6. Изменение средних значений размера очереди и дисперсии для коэффициентов загрузки р , не превышающих 0,5

участке разница составляет примерно 30 %. Исследуем этот параметр более подробно:

А(р) = Dm (р) - q(р) = рE - -р^- - р.

2(1 — р ) 2

Τочка пересечения линий соответствует за-

грузке

^ρ 0 ⁼

E + 1 2 E

» 0,5.

Максимальное значение разности соответствует загрузке

ρm

E + 1

2(2 E - 1)

» 0,25.

ная разница объясняется погрешностью процесса имитационного моделирования и влиянием корреляционных связей.

Очереди при малых загрузках. Был сгенерирован групповой пуассоновский поток со значением интенсивности λ= 100 заявок в секунду. Поток содержал пачки заявок, имеющих пуассоновское распределение чисел заявок в пачке, со средним значением k ₁ = 100 заявок в пачке и интенсивностью поступления пачек λ ₁ = 1 пачка в с, х = к 1 X 1 = 100.

На рисунке 5 показаны изменение значений числителя D m ( р ) J ( р ) в формуле (4) (сплошная линия) и изменение дисперсии D m ( р ) (точечная линия) для коэффициентов загрузки р , не превышающих 0,5.

На участках, где линии совпадают, индекс дисперсии равен единице, что означает малое влияние корреляционной составляющей. Среднее значение очереди определяется в основном дисперсией.

На рисунке 6 показаны изменение средних значений размера очереди и изменение дисперсии D m ( р ) (прямая линия) для коэффициентов загрузки р , не превышающих 0,5. На указанном

Максимальная разность А ( р m ) ® 8,3 превышает значение очереди q ( р m ) также примерно на 30 %.

Групповой поток с экспоненциальным распределением вероятностей чисел заявок в пачках, зависимых от интервалов времени между пачками

Моделирование проводилось в сравнении с групповым потоком, имеющим пуассоновское распределение вероятностей независимых заявок в пачках. Были сгенерированы два потока пачек с одинаковыми интенсивностями λ= 1 и экспоненциальным распределением вероятностей интервалов между соседними пачками. Числа заявок в пачках первого потока имеют экспоненциальное распределение вероятностей со средним значением k 1 = 100 и пропорциональны длительностям интервалов между пачками. Числа заявок в пачках второго потока распределены по закону Пуассона со средним числом заявок в пачке к 2 = 200. Это позволило для обоих потоков сделать одинаковыми дисперсии чисел заявок на интервалах обслуживания. Для каждого из потоков было сгенерировано по 10 ⁵ заявок.

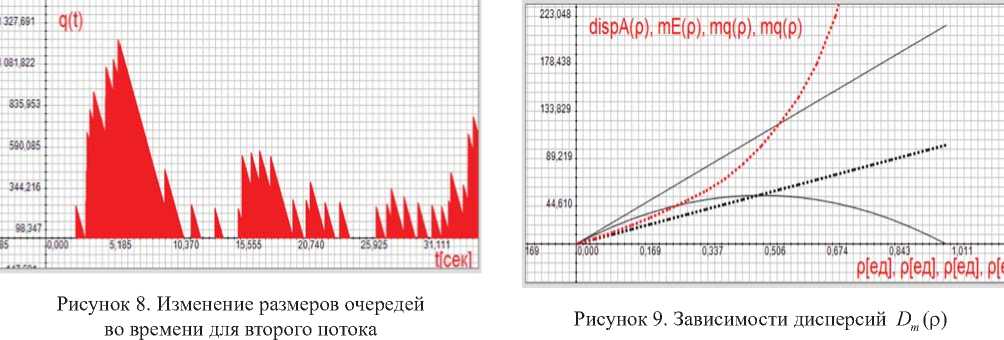
На рисунках 7, 8 показаны графики изменения очередей при коэффициенте загрузки р = 0,9 для первого и второго потоков соответственно. Из рисунка 7 видно, что очереди, возникающие при появлении пачек заявок, не пересекаются во времени и перед появлением каждой очередной пачки очередь отсутствует. Для второго потока, показанного на рисунке 8, наоборот, очереди пересекаются и максимальные значения очередей намного превышают максимальные значения первого потока.

На рисунке 9 для сравнения совмещены некоторые характеристики рассматриваемых потоков. Зависимости дисперсий D m ( р ) для обоих потоков совмещены и представлены верхней (спл ош ной) прямой линией. Зависимость очереди q ( р ) для первого потока также линейна, представлена нижней (точечной) прямой линией, имеющей угол наклона, вдвое меньший линии дисперсии, что полностью соответствует (6).

Для обоих потоков совмещены (верхняя сплошная прямая). Зависимость очереди для первого п ото ка (точечная прямая); зависимость очереди q ( р ) для второго потока (точечная кривая); зависимость mE ( р ) числителя в формуле (1) для первого потока (дуга, сплошная линия).

Аппроксимация средних значений очередей реального трафика

Анализ двух рассмотренных выше потоков показал, что они имеют принципиально различные характеристики зависимостей очередей от коэффициента загрузки. Если характеристика потока с зависимыми заявками строго линейна, то характеристика потока с независимыми числами заявок в пачках нелинейно возрастает при больших загрузках. Эти различия можно использовать, создав групповой гиперпуассоновский поток из двух таких потоков. Соответствующим выбором параметров этого потока можно получить зависимости средних размеров очередей

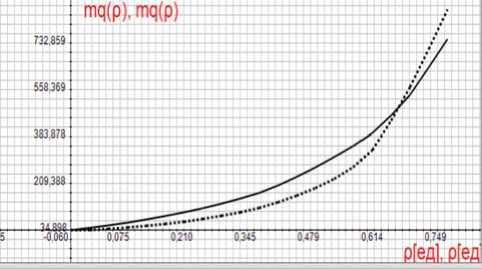
Рисунок 10. Зависимости средних размеров очередей q ( р ) для реального видеотрафика (точечная линия) и для группового потока (сплошная линия)

q ( р ) от коэффициента загрузки, весьма близкие к соответствующим характеристикам реального трафика.

На рисунке 10 показаны зависимости средних размеров очередей q ( р ) от коэффициента загрузки для реального видеотрафика и для группового потока, имеющего пуассоновское распределение чисел заявок в пачках со значением к = 420. Наблюдаем удовлетворительное совпадение. Однако причины возникновения очередей в обоих случаях существенно различны. В случае видеотрафика основной вклад в образование очередей вносят корреляционные связи. Во втором случае, наоборот, основной вклад вносит дисперсия при незначительном влиянии корреляционных связей.

Сказанное хорошо иллюстрируется представленными на рисунке 11 зависимостями дисперсий обоих потоков от коэффициента загрузки.

Размеры дисперсии чисел заявок группового пуассоновского потока при одинаковых загрузках значительно превышают соответствуюшие значения дисперсии потока реального видеотрафика.

Выводы

• 1.    Незначительное влияние корреляционных связей в групповом пуассоновском потоке

• 2.    При суммировании нескольких групповых пуассоновских потоков результирующий поток также является групповым пуассоновским потоком.

• 3.    Предложенный в работе групповой пуассоновский поток с зависимым числом заявок в пачках имеет линейную характеристику среднего размера очереди q ( р ).

• 4.    В групповом потоке с независимым числом заявок в пачках, распредленным по закону Пуассона, ковариационная составляющая числителя в обобщенной формуле Хинчина ‒ Поллачека практически отсутствует и средний размер очереди определяется значениями дисперсии D m ( р ), линейно зависящими от коэффициента загрузки.

• 5.    Принципиальное различие характеристик указанных выше потоков позволяет при их мультиплексировании получить суммарную зависимость, хорошо аппроксимирующую характеристику реального телекоммуникационного трафика.

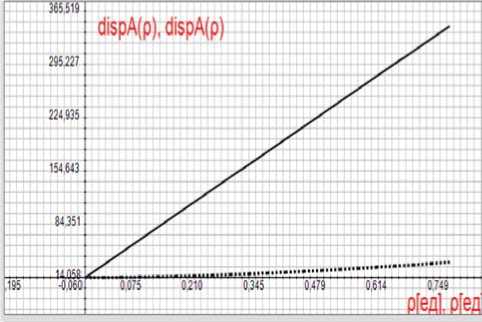
Рисунок 11. Зависимости дисперсий для реального видеотрафика (точечная линия) и для группового потока (сплошная линия)

делает его привлекательным в качестве модели телекоммуникационного трафика.