Интервальный метод определения задержек в одноприборных СМО с потоками заявок общего вида

Основным соотношением, определяющим размер очередей в системах массового обслуживания, является формула Хинчина-Полля-чека, устанавливающая зависимость между средним размером очереди и коэффициентом загрузки системы        [1-2] известного вида

- п"

Указанная формула справедлива

2(1-р)

только для пуассоновских потоков при постоянном интервале времени обслуживания.

Имеется много попыток преобразования указанной формулы [7-11], однако они оперируют в основном с пуассоновскими потоками. Поэтому возникала необходимость нахождения зависимостей, пригодных для определения размеров очередей в системах, с потоками общего вида. Такая зависимость была получена в результате применения интервального метода, основанного на определении чисел заявок, поступающих в течение интервалов обслуживания [3-6]:

= D,„(T) + 2Соу[дн(т);т((г)] р (1) 2(1-р) 2’ где q(^ – среднее значение длины очереди, Dm(r) – дисперсия числа заявок т^ на i - ом интервале обслуживания т )а Соу^-Л^т^А – ковариация чисел заявок на i-ом интервале и длины очереди q^ на предыдущем интервале. Соотношение (1) обобщает формулу Хин-чина-Поллячека, оно справедливо для любых стационарных и ординарных потоков заявок при постоянном времени обслуживания т и было получено в результате анализа уравнения баланса q^ = ^(г) + m^ - 55(т).

О, если q_i-x (г) = m_t (г) = О; (2) 1 в противном случае.

Формула (2) устанавливает зависимость между размером очереди q. (г), числами заявок т^ на текущем интервале времени и размером очереди q^ на предыдущем интервале.

Преобразование обобщеннойформулы

Выразим в (1) значения qn^) через q^), согласно (2):

Соотношение (3) также обобщает формулу Хинчина-Поллячека и также справедливо для любых стационарных и ординарных потоков заявок при постоянном времени обслуживания T.

Временные задержки в очередях

Рассмотрим временные задержки в очередях на основе анализа уравнения баланса интервалов времени между соседними заявками:

ВД =

^-i (г) + г - 0,., если Ж, (r) + t > 0 •

^4(r) + r <0„ где 0, – i-ый интервал времени между двумя соседними заявками; W.(t^ и W,.^) – промежутки времени ожидания в очереди (задержки) для заявок на i-ом и ()i–1-ом интервалах между соседними заявками, соответственно.

Как и прежде, здесь T – детерминированная переменная величина, характеризующая интервал времени обработки одной заявки. Указанная величина может изменяться в пределах, соответствующих изменению значений коэффи циента загрузки p от нуля до единицы, то есть p = t) 0 = Xt , где 0 – математическое ожидание интервалов между соседними заявками; X – средняя интенсивность потока заявок; p – коэффициент загрузки.

Анализ удобнее проводить в безразмерных относительных временных интервалах. Введем обозначения:

У(г) = [и;(г)/г]; ц(г) - [0,(r)/ r], (5)

где [и;.(г)/т] и [0,.(^)/г] – целые числа интервалов Т, укладывающиеся в ^Х⁷") и О,, соответственно, и принимающие значения 0;1;2... Уравнение баланса в указанных безразмерных единицах может быть представлено в следующем виде:

и; (г) = иу (г) +1 - ц (г), если w^ (г) +1 > ц. (г); и’,, (г) = 0, если w,._, (г) +1 < ц (г).

Перепишем уравнения как wH (г) = w,. (г) + ц (г) -1, если w,._, (г) +1 > и, (г); wM(7) = и’1.(г) + ц (г), если иу(г) + 1 < ц(г).

Введем случайную величину с\(г):

^(г) = 1, если у (г) + ц(т) > 1;

^(г) = 0, если w,.(r) + р(т) < 1.

Тогда уравнение баланса (6) может быть представлено в виде w,-, (г) = ил (г) + и^т) - З^т).      (8)

Обратим внимание на то, что неравенство ил (г) + и^т) < 1 выполняется лишь при условии, что каждое из слагаемых равно нулю, поскольку оба слагаемых неотрицательные целые числа. Это означает, что Wj^-S^t^wAtX а также и^уЗ^и^. Одновременно 8ДгУ"=ЗХг\

Возведем в квадрат обе части уравнения (8) и произведем усреднение:

vC, (г) = w² (г) + 2 ил (ф_{ (т) + Uj^T) - 2ил (г) -

Из основного уравнения баланса (7) непосредственно следует, что З^тфи^У Учи ты вая, ч то для стационарного процесса <_х(т) = Ч^Д а также, что

ИЛ (г) ■ ц (г) = w^t) • ц (г) + Cov [ил (г), ц (т)], а

”3---  -----2

и^ (г) = Uj (г) + D_v (г), получим:

2 w_; (г) [1 - ц. (г)] = 2Cov[w,. (г), ц. (г)] +

*О_и(тфиУф [1-ц(г)]

или

—^(гЕ + гСоуЕ^Дг), ц(г)] и^

Wi           2[l-t^)i        2

Соотношение (9) обобщает формулу Хинчи-на-Поллячека для среднего значения времени ожидания в очередях систем массового обслуживания с потоками заявок общего вида.

Преобразование формулы временных задержек

Обратим внимание на то, что соотношение (9) по форме аналогично (1), однако оно определяет среднее значение времени ожидания в очереди в зависимости от интервалов между соседними заявками. Коэффициент загрузки Р = т1<д=\1ифу как и следовало ожидать, обратно пропорционален среднему значению интервалов между заявками.

Определим w,^ из выражения (8):

w, (г) = ИЛ., (г) - ц (г) + ЗфУ

Ковариация

Cov [ил (г); Ц (г)] =

= [w,-! (г) - и, (г) + 3; (г) - w(r)] ■ [ц (г) - и(г)] = = Cov ^(г); ц^-^^ + ф)^!-^?-)].

После подстановки в (9) получим:

ил(г) =

-РЛ^ + гСоуЕил-Дг); ц.(г)] ! и^р 2[1-ц(й]          2

Суммирование (9) и (10) дает ил(г) =

СоуЕЕилЕгЭ + ил.,^-)]; ц(т)}

2[1-ц(г)]

Учитывая, что и^т) = Y/p, после преобразования получим ил(г) =

- Cov {[ил(г) + w_w(г)]; и, (г)} • р (11) 2(1-Р)

Введем обозначения w0,(r) = w,.(7-)-y9;

U_Qi(^ = «1(тУ р. Очевидно, что ^е/М = 1. С учетом этого соотношение (12) примет вид

₌ Cov ₍[и ₀₁ (г) + W_Q , (г)], и_@, (г)} (12)

°'                   2(1-/?)                1

Время ожидания и интервалы между заявками здесь выражены в относительных единицах, по отношению к среднему значению интервала между соседними заявками

Инвариантность корреляционных связей

Полученный результат позволяет сделать весьма важный дополнительный вывод. В соответствии с теоремой Литтла [1]:

^w&i(^ = ^_;(тр©- W; (г) • Я - qDY

Приравняв (3) и (12), получим фундаментальное соотношение

Cov{VQj (г) + q;__x (г)]; m^V

= ^— Cov {[w_e/(г) + уу_{0( ]} (t)]; l>_q/ (r)},    (13)

которое устанавливает равенство по модулю значений ковариаций при различных методах определения средней длины очереди в одноприборных СМО с потоками заявок общего вида. Знак «минус» в правой части возникает здесь потому, что с увеличением интервала между заявками размеры очередей уменьшаются. Можно сказать, что числители в (3) и (12) характеризуют динамическую составляющую мощностей потоков, которая не зависит от способа ее определения.

На рис. 1 представлены результаты моделирования (13) для реального видеотрафика. Левая часть равенства соответствует кривой «для интенсивностей», правая соответствует кривой «для интервалов между заявками». Незначительные различия между ними возникают в результате погрешностей моделирования.

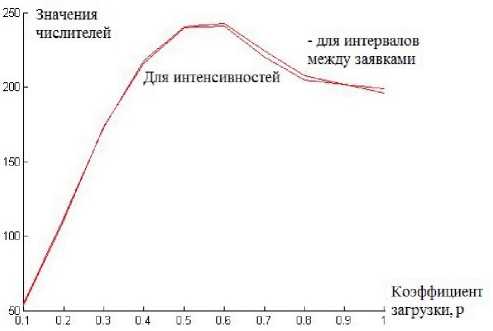
Рис. 1. Результаты моделирования равенства (13) для реального видеотрафика

Заключение

В то время как приведенное в [3-6] соотношение (3) обобщает формулу Хинчина-Полля-чека для определения среднего размера очереди в СМО с потоками заявок общего вида, полученные в настоящей работе соотношения (10)-(12) обобщают указанную формулу для определения среднего значения времени ожидания в очередях. В отличие от (3), где анализируются интенсивности заявок, по ступающих в течение интервала времени обслуживания, основными анализируемыми параметрами в рассматриваемых соотношениях являются временные интервалы между соседними заявками.

• 2.    Степанов С.Н. Теория телетрафика. Концепции, модели, приложения. М.: Горячая линия-Телеком, 2015. – 808 с.

• 3.    Лихтциндер Б.Я. Интервальный метод анализа трафика мультисервисных сетей // Модели инфокоммуникационных систем: разработка и применение. Приложение к журналу ИКТ. Вып. 8, 2011. – С. 101-152.

• 4.    Лихтциндер Б. Я. О некоторых обобщениях формулы Хинчина-Поллячека // ИКТ. Т.5, №4, 2007. – С.253-258.

• 5.    Лихтциндер Б.Я. Интервальный метод анализа мультисервисного трафика сетей доступа // Электросвязь. №12, 2015. – С. 5254.

• 6.    Лихтциндер Б.Я. Интервальный метод анализа трафика мультисервисных сетей доступа. Самара: ПГУТИ, 2015. – 121 с.

• 7.    Chan W.C., Lu T.C., Chen R.J. Pollaczek– Khinchin formula for the M/G/1 queue in discrete time with vacations // IEE Proceedings-Computers and Digital Techniques. 1997. V.144. № 4. – P. 222-226.

• 8.    Lakatos L. A note on the Pollaczek-Khinchin formula // Annal. Univ. Sci. Budapest Sect. Comp. 2008. V.29. – P. 83-91.

• 9.    Zheng F.U., Wang J. A new method for the Pollaczek-Khinchin formula // ICIC express letters. Part B, Applications: an international journal of research and surveys. 2015. V.6. – P. 1619-1624.

• 10.    Huang L., Lee T.T. Generalized pollaczek-khinchin formula for markov channels // Communications, IEEE Transactions on. 2013. V. 61. №. 8. – P. 3530-3540.

• 11. Huang L. Generalized Pollaczek-khinchin Formula for Queueing Systems with Markov Modulated Services Rates: diss. – The Chinese University of Hong Kong. 2013.