Intuitionistic fuzzy weighted sum and product method for electronic service quality selection problem

• I.    Introduction

  In early times decision making has been done with the traditional methods. With the surging increase in users of online network decision making behavior has been changed, and sharing information with the social media, provides a better reference for decision making by(Court, Elzinga, Mulder, & Vetvik, 2009)[13].Communicating sites (e.g., Facebook (FB), Twitter, Plurk, YouTube) and other types of online network services in modernistic

  years have grown dominating throughout the globe, and count of entities or businesses have emerged into communicative practices (Edelman,2010)[12]. Additionally it motivates for providing service excellency in products, outlook market tendency, and highly increases the efficiency of their advertisement on social media (Constantinides, Romero, & Boria, 2008)[16]. This also emphasizes business communications with users, to uprise communications with company websites, and search more service contingency(Michaelidou, Siamagka, & Christodoulides, 2011)[29].(Rust, 2001)[36] proposed the approach as “the foundation of service over electronic networks”. His determination was at the combination of the major establishment in the world of business. The increasing development of service ability and the rising compliance of informatory and communicating technology like a interchanging pathways, through online networks. There is abundant indications that quality of service conveyance had a conclusive blow on passionate opinion, discoverable, and commercial assistance(Cronin Brady, and Hult 2000)[25]. Additionally, this approach in which quality of service (QoS) opositively effects internet services achievement have been deep rooted (Yang & Fang, 2004; Zeithaml, Parasuraman, & Malhotra, 2002)[46,43] . Moreover, the article emphasizes on the communication which is established among quality of service and value perceived, and the encounter them according to user fulfillment, corporate apperance, and acceptations (Al Dmour, Alshurideh, & Shishan, 2014; Wu, 2014; Hu, Kandampully, & Juwaheer, 2009; Cronin, Brady, & Hult, 2000) [6,45,21,25].

Shin, 2014)[15], goals of Facebook users (Dong, Cheng, presently used service quality models do not consistently cover activities of customers on internet. The introduction of social media operation has transform the way of management of business institutions their relationship with customers or also known a Customer Relationship Management (CRM). Traditional CRM or CRM 1.0 is used more to manage consumer’s information make profitable decisions (Mohan, Choi, & Min, 2008; Greenberg, 2010)[38,31].

• II.    Literature Survey

  Particularly, social media merges electronic-service sites with Web 2.0 to represent a stage for e-commerce (Constantinides et al., 2008)[16]. Now how service quality of social commerce to be calculated has become an emerging issue. Prior to the introduction of ecommerce, an advanced approach– The network service had emerged as a brand-new business application. Additionally, internet quality of service had a heavy punch on most of the aspects of electronic business that is the reason for a trend of researchers to enforce and aggregate their research in this upcoming area of interests. The ancient evolution of the internet quality of service of literature represents numerous theoretical concepts and measuring techniques. There can be two methods to develop dimensions of quality of service of internet. The dimension attempted to determine QoS as the layout as well as properties of service providers which added attributes that leads to customer’s fulfillment through a service provider (Alpar, Porembski, & Pickerodt, 2001; Szymanski & Hise, 2000)[34,11]. Alpar et al. (2001)[34] symbolized four factors of fulfillment using a service provider’s functional benefit, knowledge of content, happiness, and accomplice. Liu and Arnett (2000)[10] additively marked the basic element of service providers qualification, those are, knowledge and quality of service, efficiency, privacy and design quality of the system, while Szymanski and Hise (2000)[11] defined various

dominating attributes in customers’ e-fulfillment, namely accessibility, advertising, site architecture, and economic compliance. And the next factor is, the analysts make efforts to advance more explicit and extensive attributes to construct the e-SQ.

The Weighted Sum method and weighted Product method is a decision making method was defined and anticipated by Zavadskas et al (2012), which has been practiced and continued in many resolutions making problems and circumstances. (Chakraborty and Zavadsk , 2014)[39] explored the method as an efficient MCDM tool while evaluating eight executing decision making problems. These advancements are the assimilation of Weighted Product Model (WPM) and Weighted Sum Model (WSM). (Zavadskas, Turskis, Antucheviciene and Zakarevicius, 2011)[24]represented this approach and contended that; the certainity of this approach strengthens the WPM and WSM. (Zavadskas, Turskis, Antucheviciene and Zakarevicius,2014)[18] suggested such new approach and demonstrated that this accumulated method executes more accurately than other methods . Recently, numerous studies organised using this approach to find a under-water port; (Zavadskas, Antucheviciene, Šaparauskas and Turskis,2011)[24] switched this to calculate the facade alternatives; (Bitarafan, Zolfani, Arefi, Zavadskas and Mahmoudzadeh,2013)[28]used the method to operate of real-time intelligent sensors for architectural monitoring of bridges; (Dėjus and Antuchevičienė,2013)[14] applied it to estimate health and safety results on the construction site; and (Hashemkhani Zolfani, Aghdaie, Derakhti, Zavadskas and Morshed Varzandeh,2013)[40]   used

WSM and WPM for decision making by considering business issues in the insight perspective.

In the decision making process, the criterion weight determination is a vital issue for the accuracy of evaluation results, for this reason, various weightdetermining methods have been launched by many authors. At a time, FSs and its extensions have gained more attentiveness in the field of decision making because of increasing intricacy and limitation of time, so that, copious MCDM methods such as COPRAS (Mishra et al. 2018a)[8], TOPSIS (Mishra et al. 2018a[8], TODIM (Mishra and Rani, 2018; Rani et al. 2018a)[8,37], VIKOR (Mishra and Rani, 2017; Rani et al. 2018b)[4,33], PROMETHEE (Rani and Jain 2017)[32], WASPAS (Zavadskas et al., 2012; Mishra et al, 2018b)[19,9] and many others have been generalized under uncertain decision atmosphere with diverse weight-determination approaches. Vijay athawale (et.al.2010)[44] preferred the most applicable CNC machine is by using TOPSIS (technique for order preference by similarity to ideal) algorithm, which has been an effective MCDM (multi criteria decision matrix) method for solving various types of complicated decision-making problems in construction domain. It was conceded that application of TOPSIS algorithm to be adequate and computable to evaluate and select the appropriate machine tool from a provided set of attributes. Abhang et al (2012)[27] suggested best lubricant in inclining process among numerous alternative lubricants in machining process of EN 31 steel work piece by using incorporate MADM. They have implemented TOPSIS model and concluded that the lubricant index assesses and ranks best lubricant at the time when steel turning operation and contribute an suitable method for solving complex MADM problems in construction domain. Nikunj et al (2012)[29] represented logical advancement for tool Insert Selection for Inclining Operation on CNC Turning Centre positioned on three well known Multiple Attribute Decision Making (MADM) approach such as TOPSIS. Mishra (2016)[2] and Mishra et al (2017)[5] proposed fuzzy TOPSIS and IF-TOPSIS method based on the similarity measure and intuitionistic fuzzy entropy for MCDM problem to rank the alternatives.This advancement is an assimilation of Weighted Product Model (WPM) and Weighted Sum Model (WSM) and TOPSIS (Technique for Order Preference by Similarity to Ideal System) algorithm that rank the rising development of services and the growing compliance of information and communication technology as a transposing medium,through Internet using facebook acoounts of top ranking social commerce companies, the criterion weight is evaluated by proposed divergence measure for IFSs . This will help in outranking the top performer with providing highest rank. Therefore, it may help consumers to consider only the ranked service providers in MP work. Additionally, it may help the consumers to chose the best service providers and also to the top brand companies improve the services by benchmarking the top rankers.

• III.    Preliminaries

  In this section, some fundamental ideas about FSs, divergence measure for FSs & IFSs are discussed. In fuzzy sets, the association of an component is stated for value from the interval [0, 1] and the non membership is simply its complement. But, actually, these assumptions do not satisfy with human perception. Thus, Atanassov (1986)[26] extended the concept of fuzzy sets (FSs) to intuitionistic fuzzy sets (IFSs) by characterizing membership function and a non membership function such that the sum of both values is less than or equal to one [Mishra (2016)[2], Ansari et al (2018)[7]].

Definition 1. (Atanassov (1986)[26]). An IFS Z on discourse set P = { p_x , p₂ , ..., p_n } is given by

^Z = {( Pi , ^a z ⁽ P i ), P z ⁽ P i )): Pi ^{G P} } ,     ⁽¹⁾

where a _z : P ^ [0, 1] and в ^: P ^ [0, 1] are the degrees of membership and non- membership of p to Z in P respectively, such that

0 <  a _z ( p , ) <  1,0 <  P z ( P i ) <  1

⁰ <  ^a z ⁽ Pi ) + P z ⁽ Pi ) <  1, ^V Pi ^e P.        ⁽²⁾

For an IFS Z in P , we call the intuitionistic index (hesitancy degree) of an element p. g P to Z the following expression:

П ⁽ P i ) = ¹ - ^a z ⁽ P i ) - P z ⁽ P i )

0 < K z ( P i ) < 1, V p g P.           (3)

For ease, the intuitionistic fuzzy number (IFN) is denoted by ф к = ( с ф , p ^ ) which satisfies а ф^ P * g [ 0,1 ] and 0 ^ + P ^ <1. [Xu(2007)]

Definition 2. Let ф = (ak, P ),   к = 1(1) n, be intuitionistic fuzzy values. Then

S ( ф к ) = ( a k - P k ) , X( Z ) = {a_k + p k ) ,     (4)

are, respectively, called the score and accuracy functions of the IFN ф _к , where §( ф ) g [ - 1,1 ] and Х( ф ) g [ 0,1 ] can be considered as net membership and accuracy degree, respectively.

Since §( ф ) g [ - 1,1 ] , when many score functions are aggregated with linear weighted summation method, it maybe appears that positive score functions are offset by negative score functions. Here, we define a new score function of IFNs as follows:

Defintion 3: Let ф _к = ( a _k , P _k ) , к = 1 ( 1 ) m , be intuitionistic fuzzy values.

Then s * (Ф, ) = 1 (8(ф,) +1),              (5)

are called a normalized score and uncertainty functions, where §( ф ) is given in (4). Obviously, S* ( ф ) g [ 0,1 ] .

Definition 4 (Xu (2007)): Let ф = ( ^ , ^ ) , к = 1 ( 1 ) n , be intuitionistic fuzzy values, then IFWA operator is defined as follows:

IFWA w ( ф , ф ₂ ,..., ф , ) =

1 - П ( 1 - a k ) w j , П P kw к = 1                    к = 1

Similarly, intuitionistic fuzzy weighted geometric (IFWG) operator is given as follows:

IFWG_w ( ф , ф 2 ,.., ф ) = П

_ к =1

wk ak

,1 - П ( 1 - P k )' ,⁽⁷⁾

к =1                 _

where w = ( w_x , w ₂,..., w_n ) L is a weight vector of ^ф к , ^k = 1 ( 1 ) ⁿ , with     ^ к =1 W k = 1,         w k g [ ^0,1 ] .

Definition 5. (Montes et al. (2015)[22] ):    Let

Y , Z e IFSs , then M : IFS ( Z ) x IFS ( Z ) ^R is called a divergence measure or cross entropy, if it fulfills the following axioms:

(D1). M ( Y , Z ) = M ( Z , Y ) ;

(D2). M ( Y , Z ) = 0 if and only if Y = Z ;

(D3). M ( YOZ Z Q Q ) < M ( Y , Z ) for every Q e IFSs ( Z );

(D4). M ( Y U Q , Z U Q ) < M ( Y , Z ) for every Q e IFSs ( Z ).

Definition 6 (Szmidt and Kacprzyk (2001)[20]. A real valued function h : IFS ( Z ) ^ [0,1] is called an entropy measure for IFSs if it satisfies the following axioms:

(P1). h ( Z ) = 0 (minimum), iff Z is a crisp set;

(P2). h ( Z ) = 1 (maximum), iff «_z ( y^ ) = в ( У /) for any У1 e Y ;

(P3). h ( Y ) <  h ( Z ) and if Y is less fuzzy than Z , i . e .

F y ⁽ yi ) <  F z ⁽ yi )     ^and      P y ⁽ У1 ) >  P z ⁽ У/ )      ^for

« y ⁽ yi ) <  ^p z ( У; ) or « y ⁽ yi ) >  « z ⁽ yi ) and P y ( yi ) <  в ⁽ yi ) for F y ⁽ xi ) >  ^v z ⁽ xi) any y ^e Y ;

(P4). h ( Y ) = h ( Y^c ).

Firstly, entropy measure for IFSs is proposed by Szmidt and Kacprzyk (2001)[20]. Here, we recall entropy measure for IFSs introduced by Mishra (2016)[2] to evaluate criteion weight of MCDM as follows:

« y ⁽ y i ) + ¹ - ^p Y ⁽ у / )

n h (Y )= 2П S

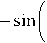
Based on Mishra et al (2016, 2017)[2,5], we propose new Jensen-Shannon divergence measure for IFSs as follows:

h ( Y , Z ) = h f  ±   ⁾ - hM ± h

v    7 l  2  J

«Y ( A)± «Z ( P,)± 2 — Fy ( P;)-pz ( Pi))    fPY ( Pi)± pz ( P,)± 2 - «Y ( Pi )-«Z ( Pi)

n

= ² S n i = 1

ln

4                  J    l                  4

f ^P Y ⁽ P i ) ± ^P Z ⁽ P i ) ± ^{2 -} « Y ⁽ P i ) — « Z ⁽ P i ) )    f « Y ⁽ P i ) ± ^P Z ⁽ P i ) ± ² — ^P Y ⁽ P i ) — ^P Z ⁽ P i )

exp l                  4                  J    l ln

f «Y ( Pi)± 1 — PY ( Pi)L_fPY ( Pi)± 1 - «Y ( Pi)) exp l           2           J l           2           J f PY ( Pi)± 1 - «Y ( Pi)L.nf «Y ( Pi) +1 - PY ( Pi )

±l         2         J p l         2

f «z (Pi)±1 -PZ (Pi))pv„f PZ (Pi)±1 -«z (Pi)) exp l            2            J l            2             J f PZ (Pi )±1 -«z (Pi)) f «z (Pi )±1 -PZ (Pi)

l          2          J^eXp l          2

WSM, WPM and TOPSIS method for IFSs

Step 1: Consider set of alternatives and set of criteria

In decision making process, our main goal is to choose the most appropriate variable from set of m alternatives S = { S j, S ₂,..., S_m } with respect to the criterion set P = { P , P ₂,..., P } . Assume that a committee (group) of t decision experts e = { e_x , E ₂,..., E_t } has been constituted to determine the most suitable alternative(s).

Step 2: Construct performance evaluation linguistic table Compute decision experts’ weights

Step 3: Construct performance evaluation table for alternatives and calculate aggregation table ^ = Г _z 1 ij m x n for smart phone selection problem

Step 4: Compute criterion weights for top brands selection problem

From eq. (8), compute the information of each intuitionistic fuzzy value in the intuitionistic fuzzy judgment matrix and get the information matrix of this judgment matrix as d = ( h )    , where h = h ( r ) .

ij n x m

Normalize the information values in the above decision matrix by using the equation hij hik =---------, h = 1,2,...,m;i = 1,2,...,n.(10)

maxh ij

And the normalized information matrix is expressed as c = ( hik)

n x m

Step 5: Determination of weights of criteria

Compute the weight vector to = (to, to,...,to)

where to - 0 and T _to = 1, by applying the given i =1

formula

m

1 - T hij w. =-----j—------, j = 1,2,...,n.      (11)

j    mn n -T T hij i=1 j=1

Step 6: Find out the positive-ideal and negative-ideal solution

In this method, the decision criteria can be classified into two criterias, benefits and cost. Let C be a collection of benefit criteria and F be a collection of cost criteria. As per intuitionistic fuzzy theory and principle of the classical TOPSIS method, positive-ideal E ⁺ and negative-ideal solution E can be defined as follows:

E ⁺

max p i j | j e B ,min p i j | j e F j ,

E. ( i = 1,2,..., m ) and the positive-ideal solution E ⁺ and the divergence measure m ( e , e ^- ) among the options E. ( i = 1,2,..., _m ) and the positive-ideal solution E ^-.

Step 8: Calculation of relative closeness coefficient (CC)

At last, relative closeness coefficient of each alternative with respect to intuitionistic fuzzy ideal solutions can be computed by using the following expression:

.   .           M ( E ,., E ^-)

S ( E ) =              i         _, i = 1 ( 1 ) m .    (14)

^V i⁷ M ( E , E ⁺) + M ( E , E )

Step 9 : Choose the highest value, denoted by m ( E_k ) , among the values M ( E_t ) , i = 1 ( 1 ) m . And hence E_k is the optimal choice.

Step 10: End.

IF-WSM and IF-WPM Methods

Steps 1-6 : As the previous method.

Step 7: Compute weighted additive and product measures

Based on WSM [Triantaphyllou and Mann (1989)][17], total relative importance of i ^th alternative as weighted sum (or additive aggregation measure) is estimated as

S =(B wn„ i = 1 ( 1 ) m ,          (15)

i     j=1 J У min v,   J e B,max v--i e F : i = 1,2,...,n , i ij         i ij

where w is the jth criterion weight,

T j

Wj = 1.

—

E

Gj’VinPij 1J eB’max Pij । j e F/’ max v j e B,min v j e F : i = 1,2,...,n , i ij         i ij

where for each j = 1,2,..., n .

IF-TOPSIS method

Step 7: Calculation of divergence measures from positive-ideal and negative ideal solution

Using eq. (9), calculate the weighted divergence measure     m ( E , E ⁺ )     among    the    options

Similarly, based on WPM [Triantaphyllou and Mann (1989)][17], the total relative importance of i ^th alternative (multiplicative aggregation measure) is calculated by

n

P i = 0 ( n_y ) j , i = 1 ( 1 ) m .              (16)

Step 8: Calculate score values of S and P by using eq. (5).

Step 9: Rank the alternatives.

Step 10: End.

Table I. Dimensions and Sub Dimensions as Criterias

Dimension (abbreviation)	Subdimensions (abbreviation)
1.Reliability (REL)	• Accurate and Reliable Service (ARS)
2.Responsiveness (RESP)	•    Accurate Description of Product (ADP) 1 •    Sincere desire to Solve Problems for Customers (SSPC) •    Promptness in Response to Requests (PRR) •    Availability of Alternative Communication Channels (AACC)
3.Functional benefit	•    A fun working environment •    A springboard for future employment •    Gaining career-enhancing experience •    High-quality products and services
4.Efficiency	•    Mobility n •    Mean SD Pain n •    Mean SD Social n
5.Privacy	•    Social context •    System privacy •    Feeling of privacy
6.Satisfaction	•    Situational satisfaction. •    Reactional satisfaction •    Expectancy satisfaction

Table II. Alternatives and Factors for E-Commerce Service Quality

Alternatives (S)	Factors (P)
• FaceBook (S 1 )	• Reliability (P 1 )
• IBM      (S 2 )	• Responsiveness (P 2 )
• Microsoft (S 3 )	• Funtional Benefit (P 3 )
• Google    (S 4 )	• Efficiency (P 4 )
• Coca-Cola (S 5 )	• Privacy (P 5 )
• American Express (S 6 )	• Satisfaction (P 6 )

Table III. Intuitionistic Fuzzy Numbers for Linguistic Attributes

Linguistic variables		IFNs
Extremely high	(EH)	(1.0,0.0)
Very high	(VH)	(0.9,0.05)
High	(H)	(0.8,0.15)
Medium High	(MH)	(0.7,0.2)
Medium	(M)	(0.6,0.4)
Medium low	(ML)	(0.45,0.5)
Low	(L)	(0.35,0.6)
Very low	(VL)	(0.2,0.7)
Extremely low	(EL)	(0.1,0.9)

Table IV. Decision Makers Weight

Decision experts	E1	E2	E3
Linguistic terms	VH	MH	H
Ifns	(0.9,0.05)	(0.7,0.2)	(0.8.0.15)
Weights	0.31	0.31	0.38

Table V. Linguistic Values Assigned by Decision Makers to the Top Brands

P1

P2

P3

P4

P5

P5

S1

E1

M

E1

:  M

E1

: L

E1

: ML

E1

L

E1

: VL

E2

ML

E2

:   L

E2

: ML

E2

: M

E2

VL

E2

: L

E3

M

E3

: MH

E3

: M

E3

: L

E3

L

E3

: VL

S2

E1

VH

E1

: M

E1

: M

E1

: H

E1

H

E1

: M

E2

H

E2

: H

E2

: H

E2

: H

E2

VH

E2

: MH

E3

M

E3

: VH

E3

: VH

E3

: VH

E3

M

E3

: M

S3

E1

VH

E1

: VH

E1

: H

E1

: VH

E1

M

E1

: H

E2

H

E2

: H

E2

: VH

E2

: H

E2

MH

E2

: VH

E3

M

E3

: H

E3

: H

E3

: VH

E3

M

E3

: H

S4

E1

VH

E1

: H

E1

: VH

E1

: H

E1

MH

E1

: H

E2

VH

E2

: H

E2

: H

E2

: VH

E2

H

E2

: H

E3

VH

E3

: H

E3

: VH

E3

: H

E3

MH

E3

: H

S5

E1

M

E1

: M

E1

: L

E1

: L

E1

M

E1

: M

E2

L

E2

: MH

E2

: VL

E2

: L

E2

L

E2

: M

E3

ML

E3

: H

E3

: L

E3

: VL

E3

L

E3

: M

S6

E1

L

E1

: M

E1

: MH

E1

: L

E1

L

E1

: M

E2

M

E2

: L

E2

: L

E2

: ML

E2

L

E2

: ML

E3

ML

E3

: ML

E3

: M

E3

: L

E3

L

E3

: M

Fig.1. Top Brands and Classification Criteria

Table VI. Aggregated Matrix for Electronic Service Quality From (6)

	P1	P2	P3	P4	P5	P6
S1	(0.74,0.179)	(0.59,0.34)	(0.53,0.47)	(0.45,0.49)	(0.32,.62)	(0.73,0.139)
S2	(0.79,0.118)	(0.83,0.11)	(0.66,0.28)	(0.84,0.10)	(0.79,0.15)	(0.64,0.31)
S3	(0.87,0.07)	(0.82,0.105)	(0.85,0.14)	(0.80,0.15)	(0.64,0.34)	(0.88,0.11)
S4	(0.90,0.04)	(0.79,0.11)	(0.80,0.11)	(0.84,0.14)	(0.54,0.24)	(0.80,0.14)
S5	(0.48,0.51)	(0.72,0.21)	(0.32,0.62)	(0.49,0.28)	(0.45,0.52)	(0.605,0.394)
S6	(0.484,0.468)	(0.423,0.524)	(0.579,0.362)	(0.48,0.28)	(0.349,0.604)	(0.498,0.431)

Table VII. Entropy Measure for Aggregated If Matrix From (9)

	P1	P2	P3	P4	P5	P6
S1	0.6362	0.9239	0.9956	0.9980	0.8910	0.5992
S2	0.4927	0.2805	0.8271	0.3971	0.5358	0.8686
S3	0.3090	0.4329	0.4399	0.5225	0.8910	0.3827
S4	0.2181	0.4818	0.4679	0.4540	0.8910	0.5090
S5	0.9981	0.6959	0.8910	0.9461	0.9940	0.9456
S6	0.9997	0.9874	0.9425	0.951	0.9208	0.9945

Table VIII. Normalised Entrpy Matrix(10)

P1 P2 P3 P4 P5 P6 S1 0.6363 0.9356 1.0000 1.0000 0.8963 0.6025 S2 0.4928 0.2840 0.8307 0.3978 0.5390 0.8734 S3 0.3091 0.4384 0.4418 0.5235 0.8963 0.3845 S4 0.2182 0.4879 0.4699 0.4549 0.8963 0.5118 S5 0.9984 0.7047 0.8949 0.9479 1.000 0.9508 S6 1.0000 1.0000 0.9466 0.952 0.9263 1.0000 C 0.1414 0.1491 0.1773 0.1654 0.1994 0.1672 w = (0.1414,0.1491,0.1773,0.1654,0.1994,0.1672)T.

Table IX. Rank Calculations of Wsm and Wpm From (11).

S	WSM	S * ( Ф )	Rank	WPM	S * ( Ф . )	Rank
S 1	(0.5735,0.3390)	0.61725	4	(0.5242,0.4125)	0.5558	4
S 2	(0.7682,0.1633)	0.8034	3	(0.7518,0.1857)	0.7083	2
S 3	(0.8183,0.1409)	0.8387	1	(0.7984,0.1673)	0.8155	1
S 4	(0.7922,0.1740)	0.5169	2	(0.4638,0.1385)	0.6626	3
S 5	(0.5564,0.4026)	0.5769	5	(0.4886,0.4469)	0.5208	5
S 6	(0.4718,0.4772)	0.503	6	(0.4604,0.4583)	0.501	6

IF-TOPSIS method

	P1	P2	P3	P4	P5	P6
S1	(0.74,0.179)	(0.59,0.34)	(0.53,0.47)	(0.45,0.49)	(0.32,.62)	(0.73,0.139)
S2	(0.79,0.118)	(0.83,0.11)	(0.66,0.28)	(0.84,0.10)	(0.84,0.14)	(0.64,0.31)
S3	(0.87,0.07)	(0.82,0.105)	(0.85,0.14)	(0.80,0.15)	(0.64,0.34)	(0.88,0.14)
S4	(0.90,0.04)	(0.79,0.11)	(0.80,0.11)	(0.84,0.14)	(0.54,0.24)	(0.80,0.14)
S5	(0.48,0.51)	(0.72,0.21)	(0.32,0.62)	(0.49,0.28)	(0.45,0.52)	(0.605,0.394)
S6	(0.484,0.468)	(0.423,0.524)	(0.579,0.362)	(0.48,0.28)	(0.349,0.604)	(0.498,0.431)
( E +)	(0.90,0.04)	(0.83,0.11)	(0.85,0.14)	(0.84,0.14)	(0.84,0.14)	(0.88,0.14)
( E - )	(0.48,0.51)	0.423,0.524)	(0.32,0.62)	(0.45,0.49)	0.32,.62)	(0.498,0.431)

Table XI. Relative Closeness of E-Sq (14)

Attributes	h ( E , E + )	h ( E , E - )	S ( E i )	Rank
E1	h ( E , E + ) = 0.0842	h ( E , E ") = 0.287	S ( Ev ) = 0.2542	5
E2	h ( E 2, E + ) = 0.0166	h ( E 2, E ") = 0.1167	S ( E 2 ) = 0.8754	2
E3	h ( E 3, E + ) = 0.00636	h ( E 3, E ") = 0.1278	S ( E 3 ) = 0.9525	1
E4	h ( E 4, E + ) = 0.1019	h ( E 4, E ") = 0.1068	S ( E 4 ) = 0.5117	4
E5	h ( E 5, E + ) = 0.1298	h ( E , E ") = 0.141	S ( E 5 )= 0.5206	3
E6	J ( E 6 , E + ) = 0.1231	J ( E 6, E ") = 0.0109	S ( E 6 ) = 0.0813	6

• IV.    Conclusions

This advancement is an assimilation of Weighted Product Model (WPM) and Weighted Sum Model (WSM). TOPSIS (Technique for Order Preference by Similarity to Ideal System) algorithm to rank the rising development of services and the increasing compliance of information and communication technology as a transposing medium, through Internet using facebook acoounts of top ranking social commerce companies, the criterion weight is evaluated by proposed divergence measure for IFSs. This will help in outranking the top performer with providing highest rank rank. Therefore, it may help consumers to consider only the ranked service providers in MP work. In this paper the service quality of e-commerce websites is calculated through comparing Weighted Product Model (WPM) and Weighted Sum Model (WSM). TOPSIS (Technique for Order Preference by Similarity to Ideal System) methods so that it may help the consumers to chose the best service providers and also to the top brand companies improve the services by benchmarking the top ranker.