Инвариантная передача сигналов с обработкой в частотной области

В [1] была предложена относительная амплитудная модуляция (ОАМ). Ее суть заключается в том, что предыдущая посылка служит опорной для последующей, а их отношение на приеме, несмотря на воздействие мультипликативной помехи с коэффициентом передачи канала К, равно отношению этих посылок на передаче. ОАМ позволяет существенно снизить влияние мультипликативной помехи. Однако влияние аддитивной помехи при этом не устраняется.

Автор данной статьи воспользовался идеей ОАМ, но при этом опорные посылки одинаковой величины выделялись им в последовательность одинаковых обучающих сигналов с их дальнейшим усреднением для снижения воздействия аддитивной помехи, а информационные сигналы различной амплитуды выделялись в информационную последовательность. В результате отношение сигналов информационной последовательности к значению усредненных обучающих сигналов также снижало воздействие мультипликативной помехи. Такой способ формирования сигналов на передаче и их демодуляции на приемной стороне позволяет улучшить помехоустойчивость предложенной структуры как минимум на два порядка по сравнению с классическими системами с ОАМ.

Данная статья посвящена синтезу алгоритма обработки информации инвариантной системой передачи информации в частотной области и анализу полученных технических характеристик.

Постановка задачи. Пусть имеется аналоговый канал связи с полосой пропускания от f _н до f _в, по которому передаются амплитудно-модулированные прямоугольной огибающей сигналы. Последовательности сигналов информационной и обучающей частей объединены в блоки.

Передаваемые сигналы подвергаются действию следующих помех: мультипликативной, описываемой изменением коэффициента передачи канала связи k(t) на определенной частоте, и аддитивной, представляющей собой белый шум с некоррелированными отсчетами и дисперсией s2 (при моделировании дисперсия принимает значение, равное 1). Помимо этого на принимаемый сиг- нал воздействуют амплитудно-частотные и фазочастотные искажения канала связи.

Будем считать, что канал связи подвержен гладким общим замираниям и поэтому можно выделить интервалы стационарности свойств канала, в частности интервалы, на которых коэффициент передачи канала связи и амплитуда отсчетов амплитудно-частотной характеристики (АЧХ) постоянны, т. е. не меняются, а также что длительность передаваемого блока не превышает длительность интервала стационарности.

Для борьбы с аддитивной помехой введено накопление с усреднением обучающих сигналов. Для этого арифметически складываются одноименные отсчеты обучающих сигналов и затем эта сумма делится на количество слагаемых.

Необходимо синтезировать алгоритм обработки сигналов, устойчивый к воздействию комплекса помех (мультипликативной и аддитивной), а также структуру системы передачи информации, позволяющую демодулиро-вать сигналы передачи в соответствии с предложенным алгоритмом с последующим анализом количественных характеристик этой системы.

Синтез алгоритма обработки сигналов. Для решения поставленной задачи потребуется, во-первых, сформировать сигнал передачи (противоположная сторона) и, во-вторых, синтезировать алгоритм обработки на приеме.

Сигнал передачи сформируем блоками (рис. 1). Каждый блок будет состоять из обучающего сигнала (пилот-сигнала) и информационного сигнала. Сигнал обучения будет одинаковым на всех последующих блоках. Для простоты формирования обучающий сигнал S об ( nT) представим в виде отсчетов равной амплитуды. В соответствии с законами цифровой обработки сигналов обучающему сигналу S _о б ( kT) соответствует энергетический спектр S об ( jk ).

Энергетический спектр информационного сигнала определим как

S (jk ) = S (jk) S (jk), (1) инфобмод где Sо6(/k) - энергетический спектр сигнала обучения; Sмод(/k) - энергетический спектр сигнала передачи. Таким образом, энергетический спектр сигнала передачи на входе блока ОБПФ будет иметь вид

[ ^S . ( jk ) - ^S _ ( jk ) ] , ;

[ ^S. ( jk )- ^S „( jk ) ] 2 ; k ;

[ ^S . ( jk )- ^S ... ok ) ]; -

В блоке ОБПФ производится преобразование отсчетов энергетических спектров в отсчеты сигнала передачи S _ин ф ( nT) , а затем в модуляторе с помощью АМ-модуляции происходит модуляция информационного сигнала.

Первыми за время T об передаются радиоимпульсы одинаковой амплитуды, представляющие собой сигналы обучающей последовательности. Значения амплитуд отсчетов обучающих сигналов на выходе канала связи впоследствии запоминаются в элементе памяти и служат для демодуляции совместно со значениями амплитуд отсчетов информационных сигналов. Кроме того, значения амплитуд отсчетов сигналов обучающей последовательности на выходе канала связи используются и при определении коэффициента передачи канала связи. Затем за время Т инф передается последовательность радиоимпульсов различной амплитуды, представляющая собой последовательность информационных сигналов. Их количество равно количеству обучающих сигналов, а время передачи информационной последовательности равно времени передачи обучающей последовательности, и поэтому T и _Н ф = T об . В дальнейшем вновь следует передача обучающей последовательности, а за ней информационной и так далее до конца передачи всего блока.

После приема обучающих сигналов значения амплитуд отсчетов обучающих сигналов в элементе памяти арифметически складываются и усредняются по количеству слагаемых для борьбы с аддитивной помехой, что повышает помехоустойчивость всей системы передачи информации.

Отсчеты информационной и обучающей последовательности сигналов и их энергетические спектры характеризуются следующими особенностями (рис. 2). Следует отметить, что амплитуды отсчетов обучающего сигнала во временной области на входе канала связи равны между собой, как и значения амплитуд отсчетов энергетических спектров обучающих сигналов, а амплитуды отсчетов сигналов информационной последовательности на входе канала связи отличаются своей величиной во временной области и имеют различные значения амплитуд отсчетов энергетических спектров сигналов. Совокупности N отсчетов информационной части во временной области соответствует N отсчетов его энергетического спектра. Аналогично совокупности N отсчетов обучающего сигнала во временной области соответствует N отсчетов его энергетического спектра.

Тогда энергетический спектр для сигнала информационной последовательности i -го блока может быть представлен в виде

S (jk) = S (jk) ■ ki( jk) ■ H i( jk) + N„( jk), (2) вых вх где k- номер гармоники; SiвЬIX(/k) - энергетический спектр сигнала на выходе канала связи на i-м блоке; Siвх(/k) -энергетический спектр сигнала на входе канала связи на i-м блоке; k(jk) - энергетический спектр мультипликативной помехи на i-м блоке; H.(jk) - передаточная харак-

Рис. 1. Структура передающего устройства:

БПФ - быстрое преобразование Фурье; ОБПФ - обратное преобразование Фурье

теристика канала на i -м блоке обработки; N ₁ i (jk ) - спектральная плотность мощности аддитивного шума сигнала информационной последовательности на i -м блоке обработки.

Энергетический спектр для сигнала обучающей последовательности i -го блока находится аналогично:

5 (jk) = 5 (jk)х i об.вых i об.вх х k( jk )■ H_( jk) + N 2i( jk), (3) где 5.об вых(jk) - энергетический спектр обучающего сигнала на выходе канала связи; 5.об ra(jk) - энергетический спектр обучающего сигнала на входе канала связи; N2i(jk) - спектральная плотность мощности аддитивного шума сигнала обучающей последовательности на i-м блоке обработки.

Следует заметить, что после усреднения сигналов обучения значения амплитуд отсчетов N _{2 i} ( jk ) будут много меньше значений амплитуд отсчетов N ₁ .(jk ) за счет эффекта накопления с усреднением. Значения амплитуд отсчетов N ₁ .(jk ) больше, чем значения амплитуд отсчетов N ₂ .(jk ) в 1 000 раз, т е. N 1 .(jk ) = 1 000 N ₂ .(jk ), при количестве усреднений, равном 1 000 [5].

Как было отмечено ранее, модулирующий параметр на передаче модулирует отношение энергетических спектров информационной и обучающей частей. Тогда для демодуляции сигналов приема необходимо поделить энергетический спектр информационной части на энергетический спектр обучающей части. В результате получим:

S i мод.вых

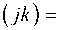
⁵_ ( jk )

5    (jk)

i об.вых

5„, ( jk ) ■ k. ( jk ) ■ H ( jk ) + N, ( jk )        Ш

____ *^вх                          *                            i                                ¹ i                                               I /I 1

S-Jjk )k'" )■ Hij)+N,Uk) ■

В силу того что значения амплитуд отсчетов энергетического спектра аддитивного шума в обучающей пос- ледовательности существенно меньше значений ампли- туд отсчетов энергетического спектра аддитивного шума информационной последовательности, то величиной N2i(jk) в выражении (4) можно пренебречь [3]. Тогда выражение (4) после элементарных преобразований сводит- ся к виду

⁵ i мод.вых ^{( jk} ) = ⁵ i вых ^{( jk} ) ⁺

₊            ^N 1i ^{( jk} )

5одвх (jk )■ ki( jk )■ Hi( jk) ’

где 5 . _модвых( /k ) - энергетический спектр модулирующей последовательности на выходе канала связи на i -м блоке; S_{i модвх}( /'k ) - энергетический спектр модулирующей последовательности на входе канала связи на i -м блоке.

По теореме Парсеваля, энергия сигнала, вычисленная во временной области, равна энергии сигнала, вычисленной в частотной области. Поэтому отношение энергии информационного сигнала к энергии обучающего сигнала сохраняется как во временной, так и в частотной области. Следовательно, результаты обработки во

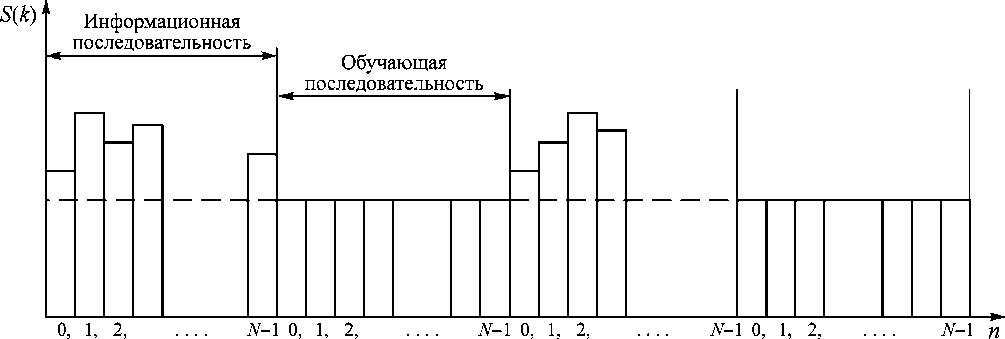
z-йблок                                   z+1-й блок

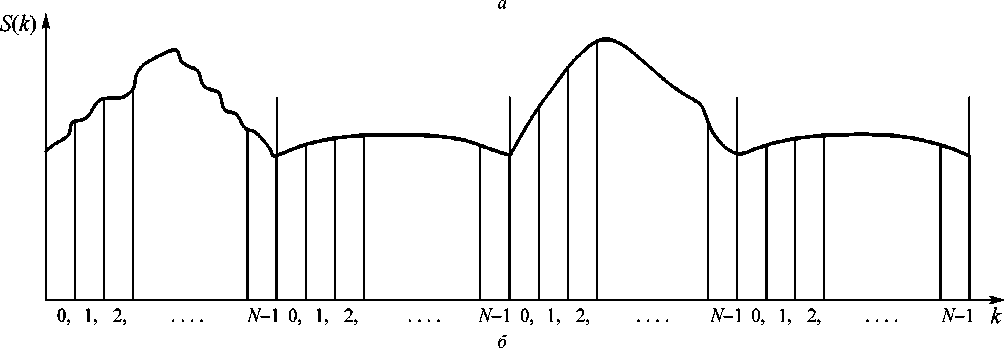
Рис. 2. Информационные и обучающие последовательности сигналов ( а ) и их энергетические спектры ( б)

временной и частотной области дают одинаковый результат, в связи с чем оценку помехоустойчивости произведем во временной области. Для этого обратимся к рис. 3, показывающему принцип такой обработки сигналов.

В точке а информационные и обучающие сигналы представлены в виде отсчетов во временной области. На выходе БПФ (точка б) сигнал представлен отсчетами энер- гетического спектра, в точке в – отсчетами энергетического спектра информационной части, в точке г – отсчетами энергетического спектра обучающей части, в точке д – отсчетами энергетического спектра модулирующей последовательности совместно с отсчетами энергетичес- кого спектра аддитивного шума, величина которого оценивается по формуле (5). В точке е сигнал представлен отсчетами модулирующей последовательности во временной области.

Для расчета вероятности ошибочного приема во временной области введем понятие инварианта.

С учетом используемой относительной амплитудной модуляции оценку значения инварианта можно найти следующим образом [2]:

L INV, ■ S    ы e

___           об    ^N ■ INV ■ ^S

INV = ^1-=-------- об- .

N ■ S.

L S об           об j=1

Будем оценивать вероятность перебора инвариантов, выбрав первым в паре самый наименьший по значению инвариант – INV1 = 1, а в качестве второго инварианта перебирая значения от 2 до 6. При переходе одного инварианта в другой происходит ошибочный прием, когда вмес- то первого инварианта в паре сравниваемых принимается второй с определенной вероятностью и, наоборот, вместо второго инварианта в паре сравниваемых инвариантов принимается первый с той же вероятностью.

Произведем расчет вероятности ошибочного приема.

Для этого воспользуемся известным подходом [2]:

z p             Ю

Р пер = P J W 2 ⁽ z ) dz + P 2 J W ⁽ z ) dz ,        (6)

-”            zp где Рпер – вероятность перехода первого инварианта во второй и наоборот; Р1 – вероятность появления первого инварианта; Р2 – вероятность появления второго инварианта; первый интеграл – это вероятность появления второго инварианта, когда послан первый; второй интеграл – вероятность появления первого инварианта, когда послан второй; zp – пороговое значение, необходимое для вычисления Рпер, при известных Р1 и Р2.

Величина z_p определяется с помощью наилучшей байесовской оценки путем минимизации Р _пер по z_p . Полагаем, что появление первого и второго инвариантов равновероятно и поэтому выбираем Р ₁ = Р ₂ = 0,5.

Для дальнейших вычислений, исходя из выражения (6), необходимо знать аналитические выражения для W ₁( z ) и W ₂( z ).

Для когерентного приема с синусоидальной поднесущей расчет функции W ₁( z ) и W ₂( z ) известен и приведен в [2].

В нашем случае прямоугольная огибающая сигнала выделяется с помощью синхронного детектора, а значит, помеха имеет нормальное распределение [4]. Поэтому мы можем использовать тот же подход для нахождения аналитического выражения плотности вероятности оценки инварианта [2].

Итак, величина оценки инварианта в рассматриваемой нами системе определяется по выражению

N

L( k ■ INV + ^( i))

INV/ = S _o6, (7) у L L( k^s об +n ( m , j ) )

L m = 1 j = 1

где в числителе INV _l – первый передаваемый инвариант, ^ ( i ) - i -е значение гауссовой помехи; в знаменателе S _о6 -значение обучающего сигнала, n ( m, j ) - j -е значение гауссовой помехи в m -й реализации сигнала S _об, k – коэффициент передачи канала связи, N – число отсчетов, взятых по огибающей INV _l или S _об, L – число обучающих сигналов.

Для расчета Р _пер необходимо знать математическое ожидание и дисперсию числителя и знаменателя выражения (7). Для их расчета воспользуемся следующими выражениями:

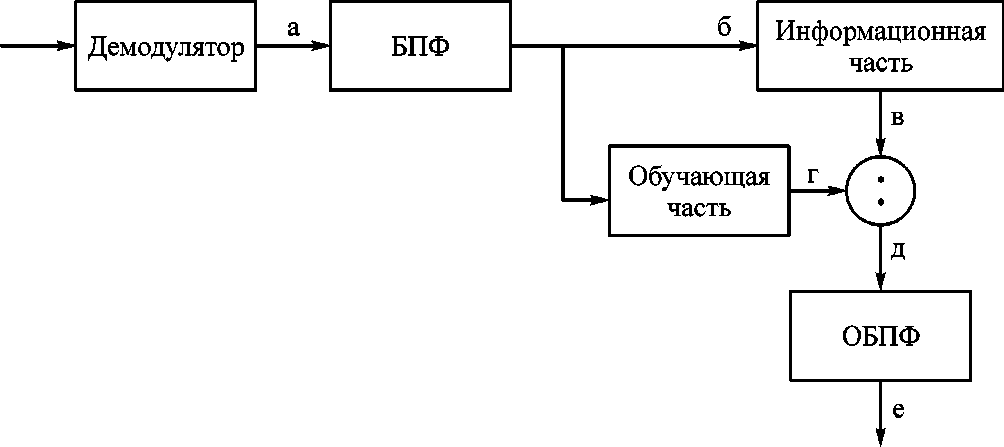
Рис. 3. Структурная схема инвариантной системы передачи информации

– математическое ожидание числителя (7) m _числ = k ⋅ N ⋅ INV _l ;                   (8)

– дисперсия числителя (7)

D числ = N ⋅ σ ²,                    (9)

где σ ² – дисперсия гауссовой помехи;

– математическое ожидание знаменателя (7) после преобразований mзнам = k ⋅ N;

– дисперсия знаменателя (7) после преобразований

N 2

D =    2 ^{σ .}

знам _LS ² об

Тогда выражение для плотности вероятности оценки инварианта с учетом (8)–(11) будет иметь вид [2]:

∞

W ( z ) = ∫

-∞

( zx - kN INV _l ) ² _{× e} ^-     2 N σ 12

e

×

2πσσ

LS ² ( x - kN ) ²

об

2 N σ ² 2      I x I dx ,

где σ ₁ = D _числ ; σ ₂ = D _знам ; L – количество сигналов обработки.

Расчет Р _пер проводился численно аппроксимацией формулы (12). Предложенная система сравнивалась с классической когерентной системой. Вероятность попарного перехода вычислялась в обоих случаях для одинаковых значений h -отношения сигнал/шум по формуле

N h2= ∑i=1k2INVli2Δt = k2INVl2

NΔtσ2σ2.

Пороговые значения Z_p рассчитывались путем минимизации Р _пер в формуле (6). Для k = 1 и INV₁ = 1, INV₂ = 2, 3, 4, 5, 6 вычисления дают результат Z_p = 1,5; 2; 2,5; 3; 3,5. Для k = 0,7 и INV₁ = 1, INV₂ = 2, 3, 4, 5, 6 получены значения Z_p = 1,5; 2; 2,5; 3; 3,5.

Результаты моделирования приведены ниже (рис. 4, 5).

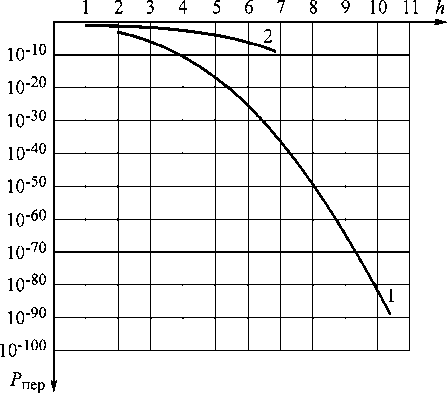
Рис. 4. Вероятность попарного перехода одного инварианта в другой при следующих заданных условиях: k = 1; INV₁ = 1;

INV2 = 2, 3, …, 10; кривая 1 – когерентный прием, инвариантная относительная амплитудная модуляция, прямоугольная огибающая; кривая 2 – классическая относительная амплитудная модуляция

Следует отметить, что особенностью любой инвариантной системы, основанной на принципе инвариантной относительности амплитудной модуляции, является то, что по каналу передаются амплитудно-модулированные сигналы, образованные INV_l и S _об. Передача этих сигналов на основе классических алгоритмов обработки информации обеспечивает невысокую помехоустойчивость [4]. И только после обработки этих сигналов в соответствии с алгоритмом частного по выражению (7) будет получена оценка инварианта, являющегося по сути числом, а не сигналом. Вероятность попарного перехода одного инварианта в другой при больших отношениях сигнал/шум определяется величинами 10^–30...10^–80 (см. рис. 4, 5). При тех же значениях отношения сигнал/шум вероятность ошибочного приема единичного символа в классических системах лежит в пределах 10^–6...10^–10.

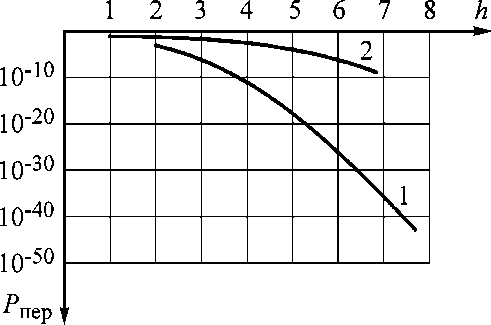
Рис. 5. Вероятность попарного перехода одного инварианта в другой при следующих заданных условиях: k = 0,7; INV₁ = 1;

INV2 = 2, 3, …, 10; кривая 1 – когерентный прием, инвариантная относительная амплитудная модуляция, прямоугольная огибающая; кривая 2 – классическая относительная амплитудная модуляция

По мнению автора, помехоустойчивость исследуемой инвариантной системы необходимо сравнивать с помехоустойчивостью аналогичных инвариантных систем, что и будет сделано в последующих работах.

Таким образом, предложена инвариантная когерентная система передачи информации и определены ее качественные характеристики. Проведенный анализ показывает, что эта система обладает высокой помехоустойчивостью: вероятность попарного перехода в инвариантной системе как минимум на два порядка меньше вероятности ошибки классического алгоритма с относительной амплитудной модуляцией. Поэтому предложенную систему следует использовать в телекоммуникационных системах, системах телеуправления и других системах, предъявляющих высокие требования к помехоустойчивости.