Инвариантно-групповой подход в теории планирования эксперимента

Получение многофакторных статистических моделей с использованием регрессионного анализа в общем случае связано с решением некорректно поставленных задач. Для того чтобы построить статистические модели с наилучшими критериями качества, необходимо применение методов теории планирования эксперимента [1; 2].

В основу классической концепции теории планирования эксперимента положена декартова ортогональная система координат и форма факторного пространства в виде многомерного прямоугольного параллелепипеда. В его вершинах сочетаются минимальные Х_{i min} и максимальные Х_{i max} уровни варьирования факторов Х_i при их задании на отрезках Х_{i min} ≤ Х_i ≤ Х_{i max} . Однако в сложных технических и технологических системах такие сочетания не всегда возможны. Реальные формы факторного пространства нередко не соответствуют стандартным, например кубу, сфере или симплексу, при этом различные фак-торы Х_i , Х_j (1 ≤ i < j ≤ k ) будутмультиколлинеарны (сопряжены) в многофакторной статистической модели как близкие к линейной зависимости [3]. В этом случае задача становится некорректно поставленной, а основным методом ее решения будет регуляризация [4–6].

Многие исследователи обращают внимание на проблему мультиколлинеарности факторов (эффектов) в регрессионном анализе.

Так, профессор Дж. Райс приходитк следующему выводу: «Если задача плохо обусловлена, то никакие усилия, потраченные на организацию изощренных вычислений, не могут дать правильных ответов, исключая случайности» [7].

По мнению Э. Фёрстера и Б. Ренца, с возрастанием коррелированности факторов вычисленные коэффициенты уравнения регрессии теряют прикладной смысл в попытке их интерпретации, так как их среднеквадратичные ошибки существенно возрастают, а сами коэффициенты становятся очень чувствительными к выборочным наблюдениям, и тогда даже незначительное изменение исходных данных «можетпривести к очень сильным сдви-гамв значениях оценок» [8].

Если решение прикладных задач отягощено исходной мультиколлинеарностью факторов, то использование известных методов планирования эксперимента, дающих наилучшие критерии качества определяемых моделей, невозможно. Необходима разработка метода и алгоритмов устойчивого оценивания коэффициентов статистических моделей в условиях мультиколлинеарности факторов.

В данной статье впервые предложены и исследованы методы получения устойчивых структур моделей и устойчивых коэффициентов при исходных некорректных условиях, которые используют топологическое отображение (гомеоморфизм) хорошо обусловленного факторного пространства – прообраза – в плохо обусловленное факторное пространство – образ [9].

Разработаны следующие методы отображения прообраза в образ [10]:

– получения функций отображения прообраза в образ с линейными (рис. 1) и криволинейными (рис. 2, 3) ограничениями факторного пространства в образе. Отображение проводится с использованием алгоритмов RASTA4, RASTA5.1 для линейного ограничения образа [9] и алгоритма RASTA4К для криволинейного ограничения [9];

– установления собственной кодированной системы координатв области образа (рис. 4, 5), для чего применяется алгоритм RASTA10 [9].

На рис. 1…3 приведены коэффициенты парной корреляции rij для натуральных значений факторов Хiо воб-ласти образа и для собственной кодированной системы координат хiо образа, а также для факторов прообраза в натуральной Хiпр и собственной кодированной хiпр системах координат; на рис. 4 натуральная x%iпр и кодированная xiпр системы координат эквивалентны друг другу; на рис. 5 x%iо является натуральной системой координат об- раза, а кодированная система координат показана линиями внутри фигуры образа.

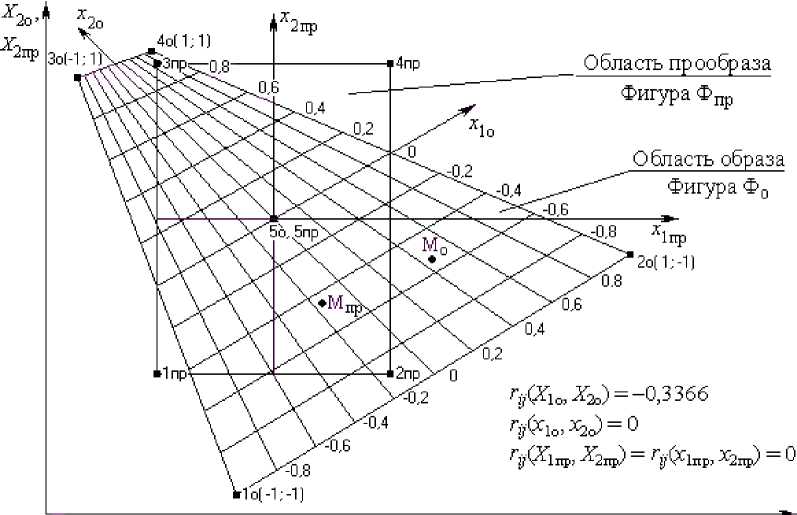
Области образа и прообраза факторного пространства с матрицами натуральных и кодированных значений факторов для отображения области прообраза (фигуры Ф _пр ) в область образа (фигуру Ф _о ) (см. рис. 1) приведены в таблице. Функции отображения прообраза f _отоб воб-раз факторного пространства следующие:

⎧⎪ X 1о = 5,2 + 1,9 x 1пр - 2,6 x 2пр - 1,3 x 1пр x 2пр , ^⎨⎪_⎩ X 2о = 5,35 + 1,05 x 1пр + 2,45 x 2пр - 0,85 x 1пр x 2пр .

Однозначность обратного отображения f _о ^- _т¹_об для функций f _отоб была установлена с использованием якобиана отображения. В области прообраза якобиан отличен от нуля и, следовательно, обратное отображение является однозначным. Для этого отображения используются ал-горитмыRASTA4 иRASTA5.1.

Представив область образа факторного пространства в кодированных значениях факторов (см. таблицу), мож-

^1о’ ^

Рис. 1. Системы натуральных и собственных кодированных координат областей образа и прообраза при линейном ограничении образа ( k = 2)

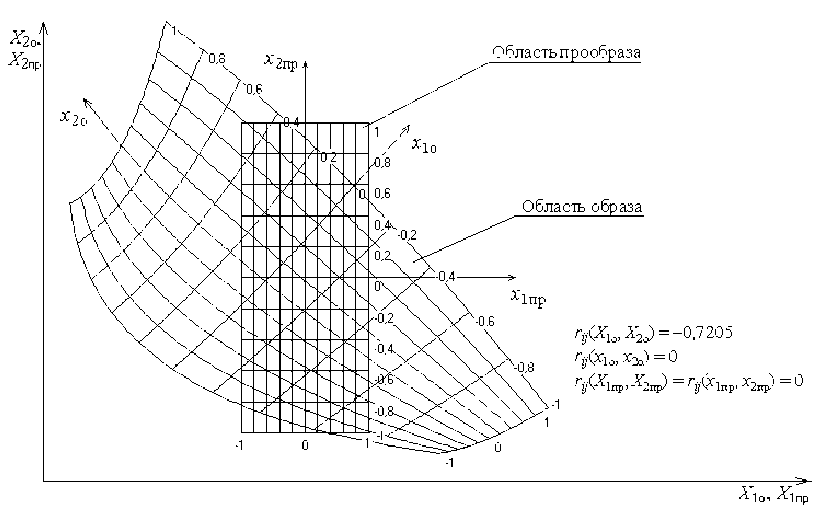
Рис. 2. Системы натуральных и собственных кодированных координат областей образа и прообраза при криволинейном ограничении образа ( k = 2)

Рабочие матрицы и планы экспериментов областей образа и прообраза факторного пространства

Области факторного пространства прообраза образа Номер точки в натуральных значениях факторов в кодированных значениях факторов Номер точки в натуральных значениях факторов в кодированных значениях факторов Х1пр Х2пр х1пр х2пр Х1о Х2о х1о х2о 1пр 3,3 2,9 –1 –1 1о 4,6 1,0 –1 –1 пр 7,1 2,9 1 –1 2о 11,0 4,8 1 –1 3_ пр 3,3 7,8 –1 1 3о 2,0 7,6 –1 1 4 пр 7,1 7,8 1 1 4о 3,2 8,0 1 1 5пр 5,2 5,35 0 0 5о 5,2 5,35 0 0 но получить в численном виде функции отображения, связывающие образ с прообразом факторного простран- ства в натуральных значениях факторов Xiпр:

Г X 1пр = 5,2 + 1,9 x , | X 2пр = 5,35 + 2,45 x _2о.

Функции отображения для прообраза факторного пространства в кодированных значениях факторов в численном виде для точки М_u будутследующими:

X, = X, ,

1uпр      1uо, x 2 и пр = x 2 и о.

Как в прямом (1), так и в обратном (2), (3) отображениях наблюдается взаимно однозначное соответствие между отображаемыми топологическими пространствами прообраза и образа. Кроме того, в функциях отображения (1)…(3) наглядно представлено взаимно однозначное соответствие между прообразом и образом и наоборот.

Ограничительные линии 1 _о 2 _о , 3 _о 4 _о , 1 _о 3 _о , 2 _о 4 _о в области образа (см. рис. 1) топологически эквивалентны ограничительным линиям 1 _пр 2 _пр , 3 _пр 4 _пр , 1 _пр 3 _пр , 2 _пр 4 _пр в области прообраза факторного пространства.

В основу изучения общих свойств геометрических преобразований в виде топологического отображения прообраза факторного пространства в образ независимо от вида ограничения факторного пространства и метода отображения следует положить понятия группы преобразований и их инвариантов.

Группа преобразований – это геометрическое преобразование фигур, удовлетворяющее следующим условиям:

• – каждая фигура Ф _{( · )} равна сама себе (свойство рефлексивности). Фигура Ф _{( · )} представляется как фигура Ф_o или Ф_пр ,и каждая из них равна сама себе;

  – если фигура Ф_пр равна фигуре Ф_o (преобразование П), то Ф_o равна Ф_пр (преобразование П^–1) (свойство симметричности). Фигура Ф_пр получается из заданной фигуры Ф_o по алгоритмам RASTA4 или RASTA4К. Посредством системы функций отображения (1) фигура Ф_пр отображается в фигуру Ф_o . Используя собственную кодированную систему координат для образа (фигуры Ф_o ), которую можно построить путем отображения собственной кодированной системы координат прообраза (фигуры Ф_пр )в образ (аналогично таблице), по выражению (2) можно отобразить Ф_o вФ_пр ;

• - если фигура Ф_пр равна фигуре Ф Пр (преобразование П 1 ), а Ф П _р равна Ф _о (преобразование П 2 ), то и Ф_пр равна Ф_o (свойство транзитивности). Преобразование П ₂ П ₁ состоит в том, что сначала производится преобразование П ₁ , а затем П ₂ .

Если эти условия выполняются, то геометрические преобразования представляют группу преобразований [11]. Ее геометрические свойства будут заключаться в сохраняющихся при преобразованиях свойствах фигур образа Фo и прообраза Фпр .

Другой вариант областей образа и прообраза факторного пространства с линейным ограничением образа представлен ниже (рис. 6).

Ортогональность факторов другкдругув прообразе при указанных преобразованиях сохраняется и в нестандартном факторном пространстве образа в собственной кодированной системе координат (см. рис. 1). Это свой-

^Зо. ^Зпр

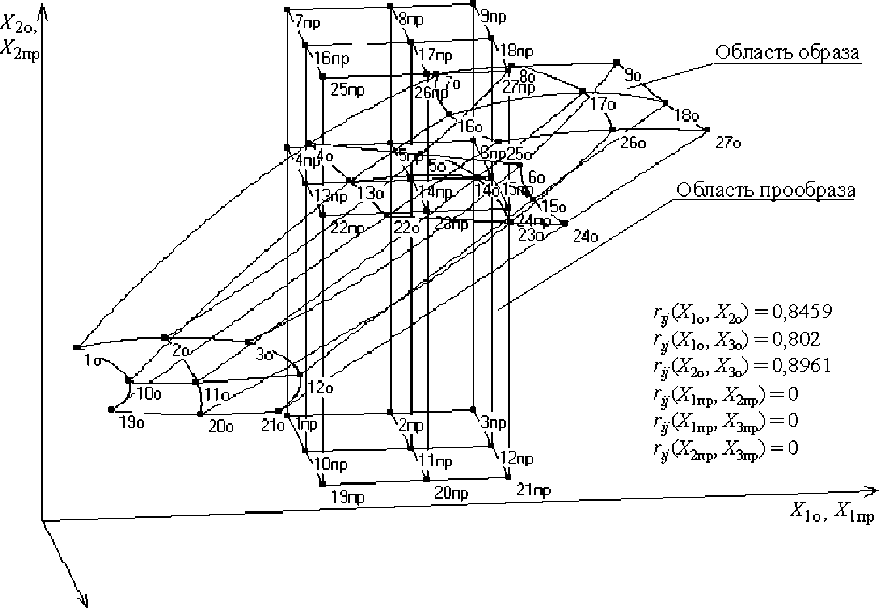
Рис. 3. Области образа и прообраза при криволинейном ограничении образа ( k = 3)

ство ортогональности является инвариантным свойством по отношению к используемому преобразованию. Рассматриваемые преобразования фигур Фпр и Фo относятся к теории непрерывных групп преобразований.

Введем понятие инвариантов в исследование отображения прообраза в образ.

Инварианты – это числа или алгебраические выражения, связанные с определенным математическим объектом и остающиеся неизменными при преобразованиях этого объекта или системы отсчета, в которой описывается объект. Характеристика геометрической фигуры и ее свойств осуществляется с помощью чисел и системы координат (или вспомогательной системы отсчета). Величины, описывающие определенную геометрическую фигуру, характеризуют и их отношение к системе координат. Свойства фигуры не должны зависеть от системы координат, т. е. должно выполняться равенство

f(x1uпр,…, xkuпр) =f(x1uo,…, xkuo), где x1uпр,…, xkuпр – координаты точек плана эксперимента в собственной кодированной системе координат для фигуры Фпр области прообраза; x1uo, …, xkuo – координаты точек плана эксперимента в собственной кодированной системе координат для фигуры Фo области образа, которая является отображением фигуры Фпр области прообраза; f– определенная функция отзначений x1(⋅) ,..., xk(⋅) координатточек плана эксперимента в собственной кодированной системе координат для фигур Ф(·).

Изучаемым свойством геометрии факторного пространства в данном исследовании является ортогональность факторов друг к другу. В этом случае функциями f(⋅) откоординат точек фигур Фпр и Фo являются парные коэффициенты корреляции rij(xiпр, xjпр) и rij(xiо, xjо), 1Јi < j ≤ k. В различных формах факторного пространства – прообраза и образа – при использовании в прообразе регулярного плана эксперимента коэффициенты парной корреляции факторов rij (xi(⋅),xj(⋅))равняются нулю и в прообразе, и в образе. Рассматриваемая геометрия факторных пространств тесно связана с теорией инвариантов. По Ф. Клейну, каждая геометрия является теорией инвариантов соответствующей группы преобразований [12].

Разработка теории непрерывных групп преобразований геометрических фигур прообраза Фпр и образа Фo , представляющих собой геометрическое выражение плана эксперимента и сохраняющихся при этом их статистических характеристик – инвариантов – в собственных кодированных системах координат, приводит к созданию инвариантно-группового подхода в теории планирования эксперимента. Этот подход позволяетполучать многофакторные статистические модели с наилучшими возможными характеристиками для нестандартных областей факторного пространства в именованной системе координат в условиях исходной мультиколлинеарности факторов в образе.

Таким образом, впервые разработана и исследована концепция инвариантно-группового подхода в теории планирования эксперимента. Данный подход ориентирован на использование для произвольных форм факторного пространства планов экспериментов, разработанных для областей в виде прямоугольных параллелепипедов.

Статистические свойства планов экспериментов для стандартных форм факторного пространства прообраза (фигуры Фпр):ортогональность факторов и их главных эффектов друг к другу в группе преобразований в собственных кодированных системах координат прообраза и образа – сохраняются и в нестандартном факторном пространстве образа (фигуры Фо ).

Дальнейшее развитие инвариантно-группового подхода в теории планирования эксперимента будет связано с понятием структуры плана эксперимента и сохранением его статистических (информационных) свойств при отображениях прообраза в образ факторных пространств (URL: .