Инвариантное к масштабу определение задержек между двумя одномерными цифровыми сигналами

Постановка задачи

Методы определения временной или пространственной задержки имеют широкий спектр применения в научных и технических задачах, среди которых: совместный анализ измерений, полученных в разное время, определение задержки в отраженном сигнале, определение положения источника звука и многих других задач из об- ласти проведения измерений, информационных технологий, медицины, радио- и эхолокации т.д [1].

Задача определения задержки одного одномерного цифрового сигнала относительно другого может быть осложнена в случае непостоянства этой задержки на протяжении процесса анализа, то есть задержка может быть переменной по времени величиной.

Рис. 1. Вектор задержек и сигналы с переменной задержкой

В таком случае каждым двум соответствующим локальным участкам сигналов будет соответствовать собственное значение задержек (см. рис. 1).

Следует также отметить, что задержка, меняющаяся во времени со значительной скоростью, приводит к частотным искажениям сигналов, то есть первая производная от функции задержек – величина, характеризующая локальную разницу в масштабах сигналов.

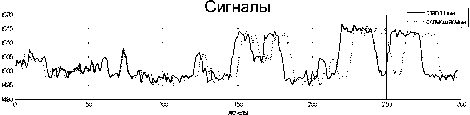
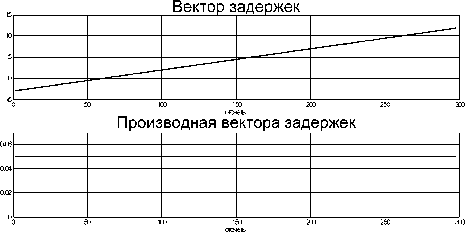
Рис. 2. Связь производной вектора задержек с разницей в масштабах

В случае, когда переменность задержки во времени обусловлена разницей в частоте дискретизации сигналов, связь между производной функции задержки и разницей в масштабах наиболее очевидна (см. рис. 2).

Другая задача, требующая инвариантности к масштабу при определении задержки, – корреляционный анализ сигналов с заведомо разной частотой дискретизации.

Решение

При оценке локальных взаимных корреляций различными способами воспользуемся окном Хемминга, которое позволяет снизить влияние разницы в масштабах сигналов, а также усилить влияние центра окна на положение корреляционного максимума (таким образом, задержка определяется в большей степени для центральной точки окна, чем для точки с наиболее выраженными корреляционными признаками).

В качестве показателя локальной коррели-рованности сигналов воспользуемся оценками корреляционного коэффициента Рте и значениями взаимно-корреляционных функций, полученных методами PHAT и ML[2] в г = О( ^РНА Т (О) и Км№ ). При этом в методах PHAT и ML интерес представляет только одна нулевая точка из всей корреляционной функции, т.к. все значения корреляционной функции кроме нулевого во взаимно-корреляционном или автокорреляционном анализе с использованием преобразования Фурье получаются циклическим смещением сигнала в окне. Таким образом, точность оценки падает с ростом н , если сигналы не являются периодическими с периодом, равным выбранному окну.

Корреляционный коэффициент Рху является нормированной величиной и определяется во временной области:

_ т^ху^-т^т^у)

где х, у – локальные участки сигналов в окнах, т – оператор определения математического ожидания.

Метод фазовой трансформации PHAT использует при определении корреляционной функции только фазы гармоник, принимая амплитуды всех гармоник равными 1, такой подход называется «выбеливанием» сигнала. Преимущество метода фазовой трансформации в том, что возрастает чувствительность к коррелированным гармоникам с малой амплитудой, но при этом снижается помехоустойчивость оценки.

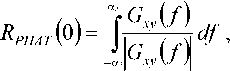
где G_xv^ ) – взаимный спектр локальных участков сигналов.

Метод максимального правдоподобия ML использует когеренцию для обеспечения взвешенного влияния гармоник на корреляционную функцию. Фазы гармоник с высокой когеренцией берутся с весом, близким к 1, независимо от их амплитуды. Такой подход обеспечивает высокую помехоустойчивость и чувствительность к гармоникам с малой амплитудой, причем rmA^=

■<уд _МД_ \^GM i-M/f

где Gn, (y) – взаимный спектр локальных участков сигналов; /YV (/) – комплексная когеренция локальных участков сигналов.

При анализе различных способов оценки взаимных корреляций было установлено, что при относительно небольшой разнице в масштабах (порядка 2%) наиболее выраженный корреляционный максимум проявляется при оценке корреляционного коэффициента.

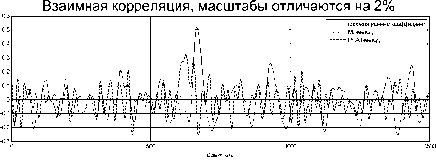
Рис. 3. Оценка выраженности максимума корреляции

Эффективность методов с фазовой трансформацией (PHAT) или метода с окном наибольшего правдоподобия (ML) очень низка (рис. 3).

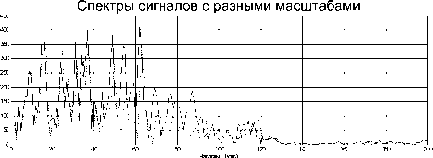
Рис. 4. Амплитудные спектры сигналов с разными масштабами

Низкая эффективность методов, определяющих корреляцию в частотной области, объясняется значительным несоответствием в частотах сигналов с разным масштабом (см. рис. 4).

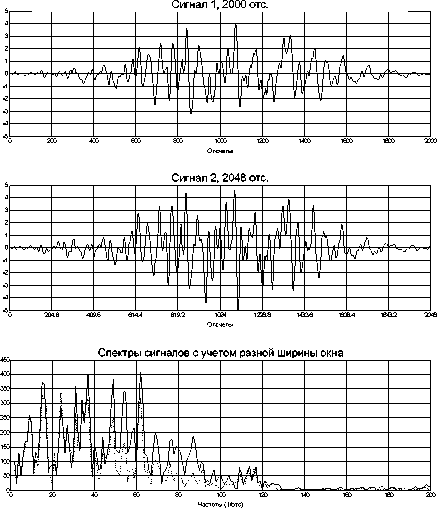
Рис. 5 . Сигналы с заведомо известной разницей в масштабах

Предположим, что разница в масштабах заведомо известна. Оценим амплитудные спектры сигналов, взятых в окнах неравной длины с поправкой на разницу в масштабах (см. рис. 5). Таким образом, для достижения полного соответствия сигналов в спектральной области достаточно отсечь гармоники, не представленные в сигнале с окном меньшей длины. Оценка корреляционного коэффициента с учетом масштаба требует передискретизации или интерполяции, что в общем виде ведет к дополнительным погрешностям.

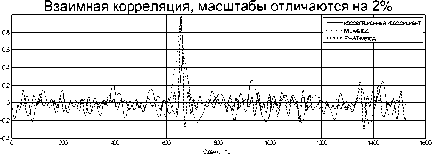
Рис. 6. Оценка взаимной корреляции при известном масштабе

Отобразим на рис. 6 результат оценки взаимных корреляций с учетом разницы в масштабах в методах MLи PHAT и метода расчета корреляционного коэффициента в стандартном виде. Для наглядности отображения в единой шкале ординат рис. 5 и рис. 6 графики RmM отображены с коэффициентом 0,143; а RpHAT^) – с коэффициентом 11,111.

В задачах, в которых масштаб заведомо неизвестен, возможен анализ задержек в некотором диапазоне возможных масштабов с достаточно малым для определения выраженного максимума шагом.

Взаимно-корреляционные функции, метод РНАТ

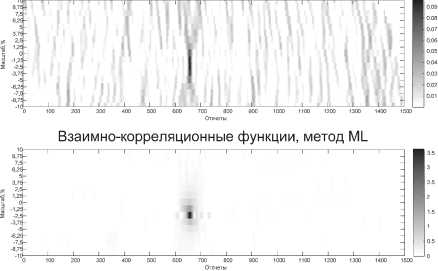
Рис. 7. Оценка взаимной корреляции при неизвестном масштабе

Для каждой разницы в масштабах анализируется взаимная корреляция сигналов. Для большей экономии в использовании ресурсов оперативной

памяти возможен отказ от полных взаимно-кор-

реляционных векторов, тогда сохраняются толь-

ко максимумы этих векторов.

Максимумы корреляции, метод РНАТ

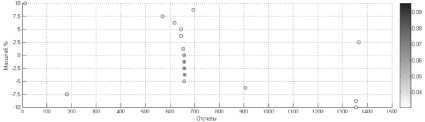
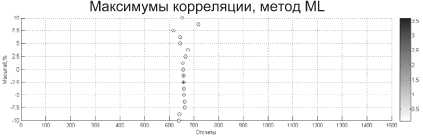
Рис. 8. Оценка максимумов взаимной корреляции при неизвестном масштабе

Как видно из рис. 8, локальная задержка анализируемого участка сигнала составляет около 650 отсчетов, масштаб второго сигнала больше масштаба первого примерно на 2,5%.

Вывод

Таким образом, располагая представлением о диапазоне, в котором может меняться относительная разница в масштабах сигналов, возможна инвариантная к масштабу оценка задержки между сигналами.

Подобный подход к проведению взаимно-корреляционного анализа без приведения сигналов к единой частоте дискретизации позволяет получать результат с меньшими вычислительными затратами и без внесения дополнительной ошибки передискретизации.

Подобный метод особенно эффективен для задач совмещения результатов измерений (для их последующей совместной оценки), полученных с применением измерительных средств, имеющих разную частоту дискретизации.