Инвариантные свойства цифровых систем

Цифровые системы обработки сигналов – это дискретные системы, описываемые разностными уравнениями и реализуемые с помощью универсальных или специализированных процессоров. При проектировании цифровых устройств полагают, что коэффициенты умножителей, а также результаты арифметических операций имеют бесконечную точность. Однако при обработке сигналов в реальных цифровых системах неизбежно возникают ошибки, обусловленные конечной разрядностью представления чисел. Эти ошибки можно разбить на две группы. Первая группа, связанная с квантованием коэффициентов умножителей, приводит к смещению расположения полюсов и нулей передаточной функции и искажению вследствие этого частотных характеристик цифровой системы. Для оценки таких ошибок можно использовать функции абсолютной чувствительности к вариациям коэффициентов умножителей, определяемые по формуле

H Ski

dH ( e^{j m} ) dk_i

Здесь H ( e^jω ) – реализуемая передаточная функция, k _i – коэффициент i -го умножителя.

или плавающей запятой). Ошибки, вызванные квантованием результатов арифметических операций, имеют случайный характер и получили название шумов квантования.

Традиционной формой реализации цифровых фильтров и корректоров является каноническая форма либо каскадное соединение звеньев первого-второго порядков. Однако рост сложности и эффективности алгоритмов цифровой обработки сигналов, развитие технологии СБИС и совершенствование архитектуры цифровых процессоров обработки сигналов привели к появлению новых конфигураций цифровых систем. В последние годы значительное развитие получили методы синтеза низкочувствительных цифровых структур, образованных каскадным соединением многополюсных секций. К их числу следует отнести решетчатые, волновые, ортогональные фильтры. Анализ характеристик волновых и решетчатых фильтров показывает, что они имеют меньшую чувствительность частотных характеристик к точности представления коэффициентов умножителей, а также уровень шумов на выходе, обусловленных округлением результатов арифметических операций.

Исследование чувствительности и шумовых свойств таких структур в аналитическом виде возможно лишь в простейших случаях. Для анализа шумовых свойств и чувствительности цифровых систем высокого порядка необходимо специализированное алгоритмическое и программное обеспечение.

Для определения потенциальных возможностей таких структур необходима информация общего, качественного характера об их свойствах. При определении минимальных границ различных критериев многопараметрической чувствительности большое значение имеют инвариантные свойства суммарной чувствительности [1, 2]. Исследование инвариантных свойств цифровых систем позволяет глубже понять механизм минимизации эффектов, обусловленных квантованием арифметических операций.

Цель работы – исследование общих свойств цифровых систем, обусловленных конечной точностью представления арифметических операций.

Удобной формой графического представления цифровых систем является сигнальный граф. Узел графа соответствует сумматору, если он имеет несколько входов и один выход, и разветвлению, если он имеет один вход и несколько выходов. Ветви графа соответствуют умножителям и элементам задержки.

Математический анализ проблемы

Для анализа характеристик цифровых систем, представленных в виде сигнального графа, используем уравнения в полном координатном базисе сигналов узлов и ветвей [3, 4]. Система уравнений цифровой системы в полном координатном базисе, записанная в блочной форме, имеет вид

Г—И   [ A ]

[Bi] —[K]-1 _[B 2 ]     [0]

Здесь [ X n ] [ X m J [ X d ]

сигналы на выходах сумматоров, умножителей и элементов за- держки соответственно, [A1 ], [A2 ], [B1 ], [B2 ] - топологические матрицы, определяющие ин цидентность ветвей и узлов схемы; [K] - диагональная матрица коэффициентов умножите-

лей. Топологические субматрицы имеют следующие размерности: [ A 1 ] - N * m, [ B 1 ] - m * N , [ A ₂ ] - N * d , [ B ₂ ] - d * N . Здесь N - число узлов в схеме, m - число умножителей, d - число элементов задержки. Элементы топологических субматриц имеют значения, равные нулю или единице. Ненулевые элементы располагаются на пересечении строк и столбцов, номера которых соответствуют номерам элементов цепи и номерам узлов, связанных с этими элементами. Например, если выход j -го умножителя подключен к i -му узлу, то элемент субматрицы [ A 1 ] , который находится на пересечении i -и строки и j -го столбца, равен 1. Остальные элементы j -го столбца нулевые. Аналогичным образом формируются и остальные топологические субматрицы.                     _{d m}

Исключая в уравнениях (1) векторы [ x ] и [ x ] , получим уравнения в сокращенном базисе узловых сигналов:

ИН A I K I » . ] + = -[ .A , I ^B , И X n ] = [ — X * ] .                    (2)

Определим чувствительность сигналов в узлах цифровой цепи к вариациям умножителя k _i . Дифференцируя (2) по коэффициенту i -го умножителя k _i , получим:

d [ K ]                                d [ x n ]

Ml dk Mix [ [Ц + ИГОМИ d

Из последнего выражения следует, что d [ X" ] = -[-[1] + [ A ][ K ][ B, ]]-i[ A jd [ K ] [ BJ[ X, j.                   (3)

dki                       -           .         . dki ,

Обозначим

[ 2 ] = [ - [] + [ A l K I B , ]].

Произведение

[ ^{T ] [ A , ]} dk i ^{B 1 ]}

можно рассматривать как вектор сигналов цифровой системы, у которой источник включен на выходе i -го умножителя. Таким образом, для расчета чувствительностей узловых сигналов к изменениям коэффициента умножителя к, необходимо выполнить два анализа. На первом шаге следует рассчитать цепь с источником, включенным на входе, и определить сигнал на выходе i -го умножителя. На втором шаге анализируется цепь, у которой источник включен на выходе i -го У--.

При проектировании систем, предназначенных для частотной селекции сигналов, больший интерес представляет, как правило, чувствительность сигнала выходного узла к вариациям всех или нескольких умножителей. Будем полагать для определенности, что необходимо рассчитать чувствительность сигнала j -го узла к отклонениям коэффициентов умножителей. Умножив левую и правую части (3) на j -й единичный вектор [ u _j ], получим: n

^[ u ^] j 7--• u ^] j ^{[ T ] -, [ A ]} ^ г^[ B ^][ X " ^]                        (4)

1                                                                                                J

Произведение - [ u ] ' [ T ] ^{- 1} можно рассматривать как вектор узловых сигналов цифровой системы, матрица коэффициентов которой является транспонированной по отношению к матрице коэффициентов исходной системы:

^

[ T ]=T] -.

Такую систему называют присоединенной, или транспонированной. При этом источник сигнала, равный -1, подключается к узлу, являющемуся выходным для исходной системы. Символом “Л” будем обозначать матрицы и переменные, относящиеся к транспонированной структуре.

Итак, в соответствии с формулой (4) чувствительность к вариациям параметра k i можно определить, выполнив анализ исходной и транспонированной систем. Функция чувствительности рассчитывается затем по формуле

.=[> i [.1 ^ 14.• ]. (5)

Обратимся теперь к анализу шумов округления цифровых систем.

Рассмотрим сначала случай арифметики с фиксированной запятой. Эффекты квантования результатов операций умножения учтем, включая источники шума e ( n ) на выходах умножителей. Структурная схема, моделирующая эффекты округления на выходе умножителя в системе с фиксированной запятой, показана на рис. 1.

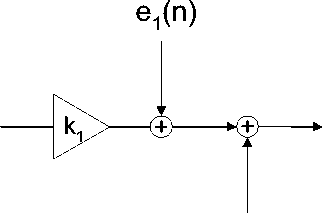
Рис. 1. Шумовая модель умножителя, использующего представление чисел с фиксированной запятой

В соответствии с этой схемой умножитель, вычисляющий произведение с конечной точностью, заменен идеальным умножителем и источником шума округления. Дисперсия шумов округления на выходе цифрового фильтра определяется передаточными функциями от выходов умножителей до выхода всей цепи:

f Ы--   fSIHi Z1

j -

Если все операции перемножения выполняются с одинаковой разрядностью, то о спектральной мощности шумов квантования на частоте ю можно судить по коэффициенту усиле-"ия шума', „

G n I ^H - e " ) .

Здесь H i (e j ) - передаточная функция от выхода i -го умножителя до выхода цифровой схемы.

Для определения этих передаточных функций запишем уравнения цифровой системы в смешанном координатном базисе сигналов узлов и умножителей, полагая, что на выходе каждого умножителя включен единичный источник:

- [ 1 ] + _Z - [ A ₂ ][ B 2 ] [ B 1 ]

гA11 ifX"]

-[K ]-1 JL[Xm 1

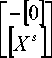
Здесь [ X^s ] - вектор размерности n m , каждый элемент которого равен единице. Исключая вектор [ X m ], получим

[ - [ 1 ] + [ A ][ K ][ B 1 ] + _Z ^{- 1} [ A 2 ][ B 2 ] ] X ] = - [ A ] [ X^s ] .                             (6)

Обозначим

^{7 ] [ [ 1 ]+[} A ^][ K ^][ B ^] + _Z ^[ A ₂ ^][ B ₂ Ц.

Из последних соотношений следует, что вектор узловых сигналов, обусловленный действием источников на выходах умножителей,

[X" ]=—7 Г [Ai ][Xs ].

n

Для того чтобы определить сигнал только выходного узла x_iⁿ , умножим левую и правую части последнего равенства на i -й единичный вектор [ u i ] t . В результате получим:

X ” = —№ И A 1 ] [ X - ] ■

Произведение - [ u i ] t [ Г ] ¹ = [ X ] представляется как вектор сигналов в узлах присоединенной системы, имеющей матрицу коэффициентов, транспонированную по отношению к исходной. Единичный источник при этом подключается к узлу i , являющемуся выходным для исходной цепи. Коэффициент усиления шумов квантования определим по формуле

G -I=| М - | ^[ Л Х ' ^] . ⁽⁷⁾

Таким образом, коэффициент усиления шумов квантования равен взвешенной сумме квадратов модулей сигналов на входах умножителей в транспонированной структуре. Этот факт - следствие свойства взаимообратимости структур, представленных сигнальным графом [5]. Произведение [ A 1 ] [ X^s ] является вектором, j -й элемент которого равен суммарному числу умножителей, выходы которых подключены к узлу с номером j.

Рассмотрим теперь цифровые системы с плавающей запятой. Использование арифметики чисел с плавающей запятой приводит к появлению шумов квантования не только на выходах умножителей, но и на выходах сумматоров. Моделирование такой системы требует включения источников шума, как на выходах умножителей, так и на выходах сумматоров [5]. Это существенно усложняет анализ. Шумовая модель, учитывающая округление результатов при выполнении операций умножения и суммирования, показана на рис. 2.

е1(п)          е2(п)

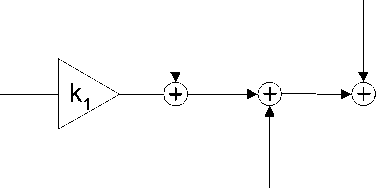
Рис. 2. Шумовая модель при выполнении операций умножения и суммирования с плавающей запятой

Выведем соотношения, позволяющие определить спектральную плотность мощности шумов округления на выходе цифрового устройства, использующего арифметику с плавающей запятой. Запишем уравнения в смешанном базисе сигналов узлов и умножителей:

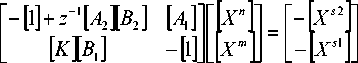
Здесь [ X^s * ] и [ X^{s 2}] - сигналы источников, включаемых на выходах умножителей и сумматоров соответственно. Исключая вектор сигналов умножителей, получим уравнения в базисе узловых сигналов:

[ - [ * ] + [ A *I K ][ ^ 1 1 + - Ч A ₂ ][ B ₂ 11 X n ] =— [ A * ] [ X * ] — [ X ² ] -

Обозначим

[ T ] = [ - [ 1 ]+[ A 1 K I B ]+Х'[ ,A , I B 2 Ц .

ТЧ                                                 -                                                                         Г'Г’1 -1

Вектор узловых сигналов найдем, умножив левую и правую части на [ T ] :

[ x n ] =- [ T Г ( [ A ] [ x s 1 ] + [ x s 2 ] ) .                                    (8)

Для определенности будем считать, что выходным является узел с номером j . Выходной сигнал найдем, умножая левую и правую части (8) на j -й единичный вектор и ]:

u j 1^[ xn ^ j TA l     x s ² 1.

Произведение

„ = »  = e one        [1 о"e^1   [u^"[^ e C                  e о представляет вектор сигналов в узлах присоединенной си стемы с матрицей коэффициентов,

A

[T ^{] [ T ]}.

Итак, сигнал на выходе системы, обусловленный действием дополнительных источников, определяется выражением

X . "- [ X n I A .X^ Ч X - 21.                                (9)

Сигналы дополнительных источников пропорциональны сигналам на выходах умножителей исходной цепи. Последние можно определить по формуле

[ X ] m = [ K ][ S 1 ][ X^- ] .

С учетом равенства (10) формула (9) примет вид

X i- l X - ] - [[ < 11 K I ^{B ]} - i][ X 4

Включим на входах исходной и транспонированной схем единичные источники. Тогда коэффициент усиления шумов к вантования в цифровой цепи, использующей представление чисел с плавающей запятой, -                                       ■

G ( ю ) = [ X^- ] t [ А_х ][ K ][ B 1 ][ X^- ] + [ X^- ] t [ X^- ].                       ⁽¹¹⁾

Спектральная плотность мо щности шума на выходе цифровой системы равна

Ф ( _Z ) = ^ G ²( w ) Ф _х ( _Z ) ,                                     (12)

где Ф _x ( z) - спектральная плотность мощности входного сигнала.

Полученные соотношения показывают, что на уровень шумов округления на выходе цифровой системы влияет не только конфигурация, но и способ представления чисел. Необходимо подчеркнуть также, что при расчете чувствительности и уровня шумов округления цифровых систем большое значение имеет анализ транспонированной структуры. По существу, шумовые свойства и чувствительность цифровой системы зависят в первую очередь от свойств транспонированной структуры. Этим можно объяснить тот факт, что между функциями суммарной чувствительности и уровнем спектральной плотности мощности шумов округления на выходе цифрового устройства существует тесная связь [5].

Исследования инвариантных свойств цифровых систем

Рассмотрим сначала свойства функций чувствительности исходной и транспонированной структур. Функция чувствительности цифровой цепи к отклонениям коэффициентов умножителей определяется формулой (5).

В уравнениях для транспонированной цепи матрицы [A1 ], [A2 ] и [B1 ] , [B 2 ] меняются местами. Формула, определяющая критерий суммарной чувствительности транспонированной цифровой системы, примет вид dj=[X-1[»,l dJK [

Нетрудно видеть, что функции чувствительности, определяемые выражениями (5) и (13), одинаковы.

Сказанное позволяет сформулировать следующее свойство.

Свойство 1. Функции чувствительности узловых сигналов цифровой системы к вариациям коэффициентов умножителей одинаковы для исходной и транспонированной структур.

Сформулированное свойство справедливо как для суммарных критериев, так и для чув-ствительностей к изменениям коэффициентов отдельных умножителей.

Обратимся теперь к исследованию инвариантных свойств спектральной плотности мощности шумов квантования на выходе цифровой системы. Коэффициент усиления шума в цифровом устройстве, использующем представление чисел с плавающей запятой, определяется выражением (5). Коэффициент усиления шума в транспонированной структуре

__

G (с о ) = [ х " ] [ 8 ,1 ^ р, ] х "  ]+ [ x n ] [ X "  ] ■

Нетрудно убедиться, что для цифровых фильтров любой конфигурации выполняется равенство

Сформулируем этот результат в виде свойства 2 : спектральная плотность мощности шумов округления на выходе цифровой системы, использующей представление чисел с плавающей запятой, одинакова для исходной и транспонированной структур.

Рассмотрим теперь шумовые свойства цифровых систем, использующих арифметику с фиксированной запятой. В этом случае коэффициент усиления шумов квантования цифрового устройства определяется выражением (11).

Для транспонированной структуры сигналы узлов, обусловленные действием источников на выходах умножителей, определяются соотношением

^[ X n ^]=- [ ^ П B 1 ] [ X^s ] .

Если выходным является узел с номером i, то сигнал этого узла x =-[u И? -8 Iх*].

Таким образом, спектральная плотность мощности шумов округления на выходе транспонированной структуры

G И 2 -| ^{X ]}1² 1 B l ^X ]■                              04)

Сравнение соотношений (11) и (14) позволяет сформулировать свойство 3: спектральная плотность мощности шума квантования на выходе цифровой системы, использующей арифметику с фиксированной запятой, одинакова для исходной и транспонированной структур, если выполняется равенство

[ A ] = [ B i ] t -                                                               (15)

Отметим, что условие (15) выполняется для многих распространенных структур цифровых фильтров. Оно справедливо, например, для БИХ-фильтров канонической формы.

Выводы

• 1.    Получены матричные соотношения для расчета чувствительности и спектральной плотности мощности шумов квантования цифровых фильтров, реализуемых с помощью арифметики с фиксированной и плавающей запятой.

• 2.    Исследованы инвариантные свойства чувствительности и шумов округления исходных и транспонированных цифровых цепей. Показано, что чувствительность, а также уро-

• вень шумов округления в случае использования арифметики с плавающей запятой одинаковы для исходной и транспонированной структур цифровой цепи.

• 3.    Определены условия, при которых свойство инвариантности шумов округления справедливо в случае использования арифметики с фиксированной запятой.

Статья опубликована при поддержке Программы развития Сибирского федерального университета.