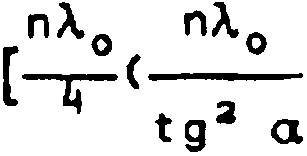Инвариантные свойства элементов дифракционной квазиоптики

Развитие элементов интегральной оптики, средств ввода-вывода оптической информации, обработки изображений, создание основ элементной базы оптических ЭВМ стимулируют разработку новых элементов дифракционной квазиоптики (ЗДК). Основные достоинства ЭДК заключаются в возможности применения планарной технологии изготовления, высокой разрешающей способности, мало отличающейся от дифракционного предела, наличии частотных свойств и т.п. Изучение свойств ЭДК и разработку их новых типов удобно проводить в СВЧ диапазоне, где соблюдается масштабный эффект. Кроме того, ЭДК СВЧ диапазона представляют собой и значительный самостоятельный интерес.

Исследованиям фокусирующих и частотных свойств простейшего дифракционного квазиоптичес ко го объектива (зонной пластины (ЗП)) посвящено достаточно много работ. Так, в работе [1] показано, что в миллиметровом диапазоне длин волн фазоинверсная ЗП по своим фокусирующим свойствам эквивалентна плосковыпуклой СВЧ линзе с гиперболической поверхностью, но из-за значительно меньшей толщины обладает гораздо меньшими потерями СВЧ мощности на поглощение в материале объектива. В работе [2] в приближении дифракции Френеля показано, что ЗП обладает разрешением, как и идеальный безаберрационный объектив. Подробно частотные и фокусирующие свойства ЗП, предназначенной для преобразования расходящегося сферического волнового фронта в сходящийся сферический при осевом точечном источнике излучения, представлены в работе [3] . Показано, что светосильный объектив на основе ЗП сохраняет свои фокусирующие и частотные свойства в широком спектральном диапазоне длин волн, отличных от номинальной (то есть от той, на которую рассчитывалась ЗП). При этом ЗП с относительным отверстием 1/2 и апертурой D/X “200 обеспечивает поле зрения порядка 30 градусов при числе элементов изображения в кадре не более 50х50 [4].

В ряде работ индийских ученых [5“7] рассматриваются дифракционные объективы на поверхностях вращения второго порядка (сфере [5], параболе [?]). В этих работах получены соотношения для радиусов зон Френеля на соответствующих поверхностях; в приближении геометрической оптики проанализировано влияние точности установки излучателя в фокусе на величину смещения его изображения вдоль оптической оси. На основе аналитических расчетов, проведенных в приближении Френеля, показано, что у объектива со сферической поверхностью полуширина распределения интенсивности поля вдоль оптической оси в области фокуса несколько уже, чем для ЗП, однако уровень боковых лепестков рассеяния выше [5].

Что касается дифракционного объектива, выполненного на параболической поверхности, то из результатов работ [6, 7] следует, что по сравнению с ЗП и сферическим объективом "параболический" обеспечивает наиболее узкое распределение интенсивности поля вдоль оптической оси в области фокуса. Кроме того, в работе [?] показано, что при изменении частоты излучения примерно в 1,35 раза его фокусное расстояние изменяется в 2 раза.

Изучение информативных свойств (частотных и фокусирующих) светосильных одно и двухкомпонентных дифракционных объективов на параболической поверхности проведено в работе [8]. Показано, что при относительном отверстии 1/2 и апертуре D/X -40 такие фокусирующие системы обеспечивают поле зрения не менее 20-30 градусов соответственно при разрешении, мало отличающемся от дифракционного предела, и при сохранении Фокусирующих свойств в диапазоне длин волн, отличных от номинальной до ±20?. Отмечено также, что дифракционная квазиоптика на неплоских поверхностях обладает свойством невзаимности, заключающимся в том, что при расчете объектива следует учитывать ориентацию источника и приемника излучения относительно вершины его поверхности.

В то же время известные работы носят частный характер, не позволяют установить взаимосвязь информативных свойств плоских и неплоских ЭДК.

Целью настоящей работы является установление инвариантных свойств элементов дифракционной квазиоптики, выполненных на произвольной поверхности вращения второго порядка.

Частотные свойства

Не снижая -общности задачи, рассмотрим для наглядности ЭДК, преобразующий плоский падающий волновой фронт в сходящийся сферический. Записывая выражения для эйконалов дифрагированной и опорной волн, легко показать, что дискретная фазовая функция пропускания дифракционного объектива (радиусы зон Френеля) определяется из условия (для произвольной формы поверхности):

v (В-хп)2+Уп=В-хп+п у )                                                (1)

где

В - расстояние от вершины объектива до области фокусировки; XQ - номинальная длина волны; (xnz уп) - декартовы координаты границы n-й зоны Френеля (рис. 1).

Для случая падения электромагнитной волны на вогнутую поверхность дифракционного объектива следует поменять знак при хп.

Для определения частотных свойств объективов на неплоских поверхностях из выражения (1) необходимо выразить величину В:

y^-Cn £)2

^Bn^c^ = — Fa--- * ^xn-                                          (2)

Подставляя в (2) значения координат зон Френеля рассматриваемого объектива, получаем искомые зависимости.

Полученное выражение (2) позволяет сделать важный вывод о частотных свойствах дифракционных объективов, выполненных на произвольной поверхности вращения. В самом деле, найдем асимптотики границ рабочего спектрального диапазона длин волн объектива на произвольной поверхности. Минимальная длина волны находится из (2), если знаменатель приравнять нулю:

• 1    n v

Максимально возможная длина волны определяется из условия равенства числителя выражения (2) нулю:

^•тах-* ™ ^хп+^п^                                                           ^*)

где Rn=(x2+y2)l/2, что при уп»хп дает 2

^-тах"* Й^п+Уп5 *

Сравнивая полученные оценки для рабочего спектрального диапазона элементов дифракционной квазиоптики на произвольной поверхности вращения (3)—<4>, можно сделать следующие выводы:

• -    максимально возможная длина волны объектива не зависит от направления падения излучения относительно вершины поверхности объектива и определяется стрелкой прогиба данной поверхности;

• -    при падении электромагнитного излучения со стороны вершины объектива его рабочий спектральный диапазон шире, чем в противном случае;

• -    скорость изменения фокусного расстояния от относительной расстройки длины волны при падении излучения со стороны вершины поверхности меньше, чем в противоположном случае.

Приведенные аналитические зависимости наглядно показывают, что частотные свойства рассматриваемой дифракционной квазиоптики существенно отличаются от аналогичных свойств ЗП (плоской квазиоптики), у которой стрелка прогиба поверх ности равна нулю.

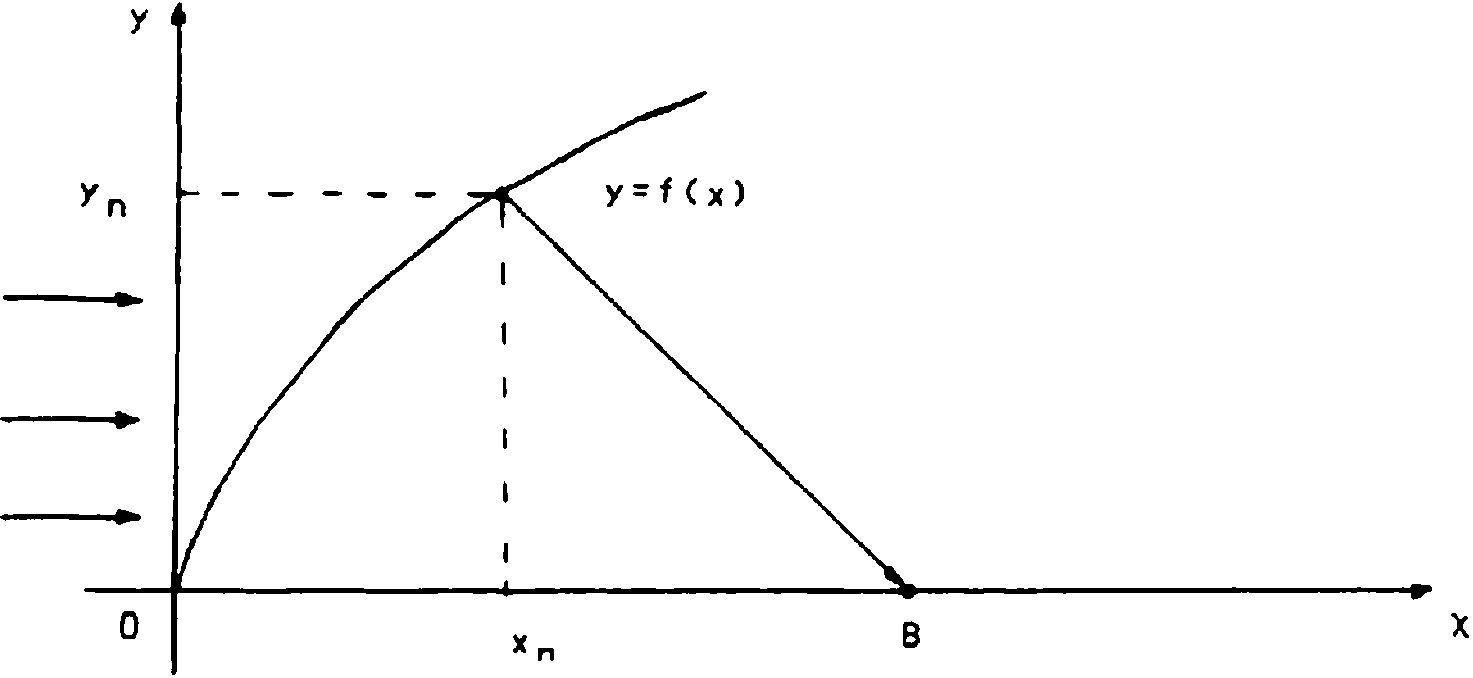
Рис. 1. Схема расчета элемента дифракционной к.вазиоптики на поверхности вращения второго порядка

Указанные особенности частотных свойств дифракционной оптики на неплоскои поверхности свидетельствуют о том, что выбором формы поверхности объектива и ее ориентацией в пространстве возможно управлять его частотными свойствами -как усиливать их, так и ослаблять.

Продольное разрешение

Рассмотрим продольное разрешение (глубину резкости) "неплоских" объективов. Следуя работе [з], из условия синфаэности излучения в точке В и противофазности его в некоторой точке В+Д2 легко получить следующее выражение для продольного разрешения Да:

<.) фа f х[св ; хп)> ♦ у’] '/, = - ^----------------------------------------  ’                             (5)

2[((В ; хп)2 + у2)1/а - (В i хп) ± у где знак (±) при хп относится к выпуклому (+) и вогнутому (-) объективам соответственно. Знак (±) при X относится к положению первого минимума распределения интенсивности поля вдоль оптической оси дальше точки В (+) и ближе ее (-).

Из (5), в частности, следует, что выбором стрелки прогиба поверхности объектива хп возможно регулирование его продольного разрешения и глубины резкости. Так, при уп»(В-хп) и уп»Х из (5) для вогнутого объектива получаем, что а^1* ; Х/2.

Для выпуклого объектива при уп«(В + хп) и (В+хп)>>Х соответственно имеем

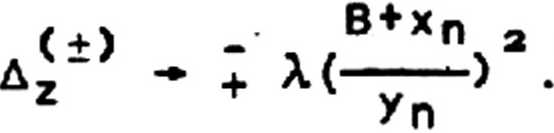
Указанные особенности поведения глубины резкости дифракционного объектива на неплоской поверхности позволяют, в частности, создать системы, обладающие значительно большим коэффициентом усиления, чем известные квазиоптические дифракционные объективы.

Дифракционный интеграл Френеля-Кирхгофа

Теоретические исследования фокусирующих и частотных свойств дифракционной квазиоптики на поверхностях вращения второго порядка проводились в форме вычислительного эксперимента с использованием скалярной теории дифракции.

Рассмотрим вычисление дифракционного интеграла Френеля-Кирхгофа в трехмерном случае (рис. 2). Пусть образующая поверхности элемента ЭДК описывается уравнением вида: r = f(z) .

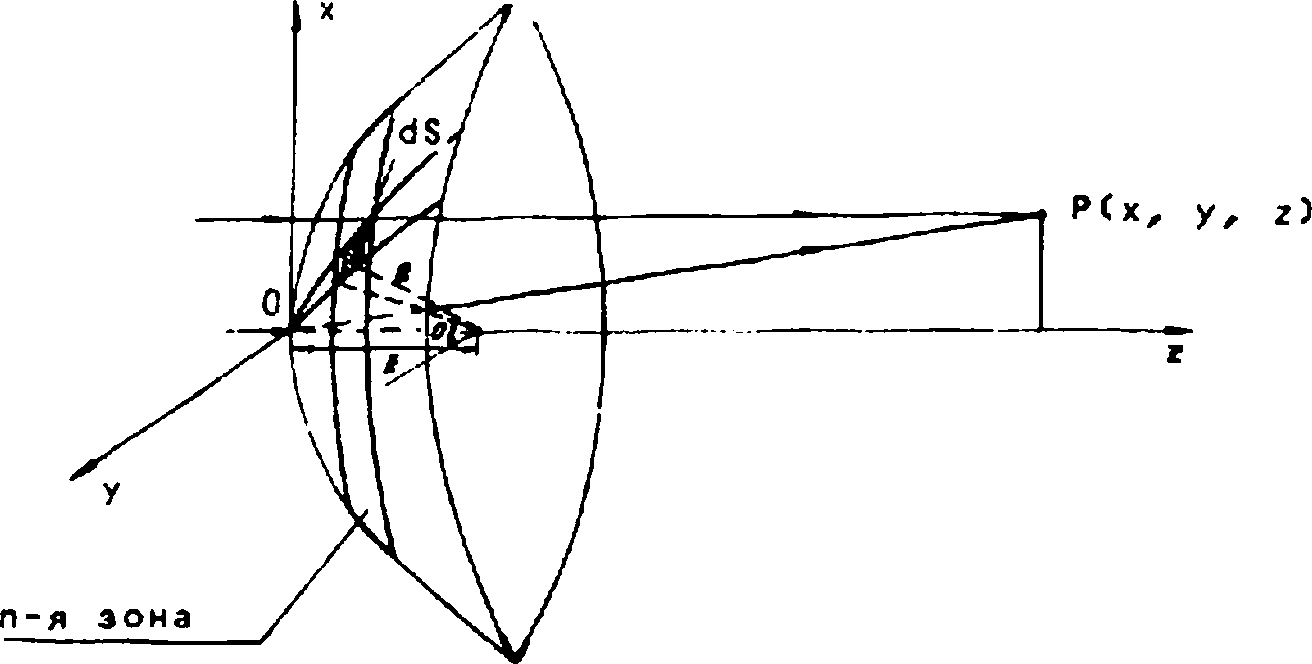
Рис. 2. Расчет дифракционного интеграла

Тогда элемент площади можно записать в виде dS = г Г1 + <^)3] Vadzde.                                                    <6)

• ^L dz ^J

Для точки наблюдения Р с координатами (xlZ ylZ z5) в случае падения на дифракционный объектив плоского волнового фронта дифракционный интеграл записывается как zn 2п

Un =   / / ^^ exp(-i ^ Q)dS,                                    (7)

П-1

где

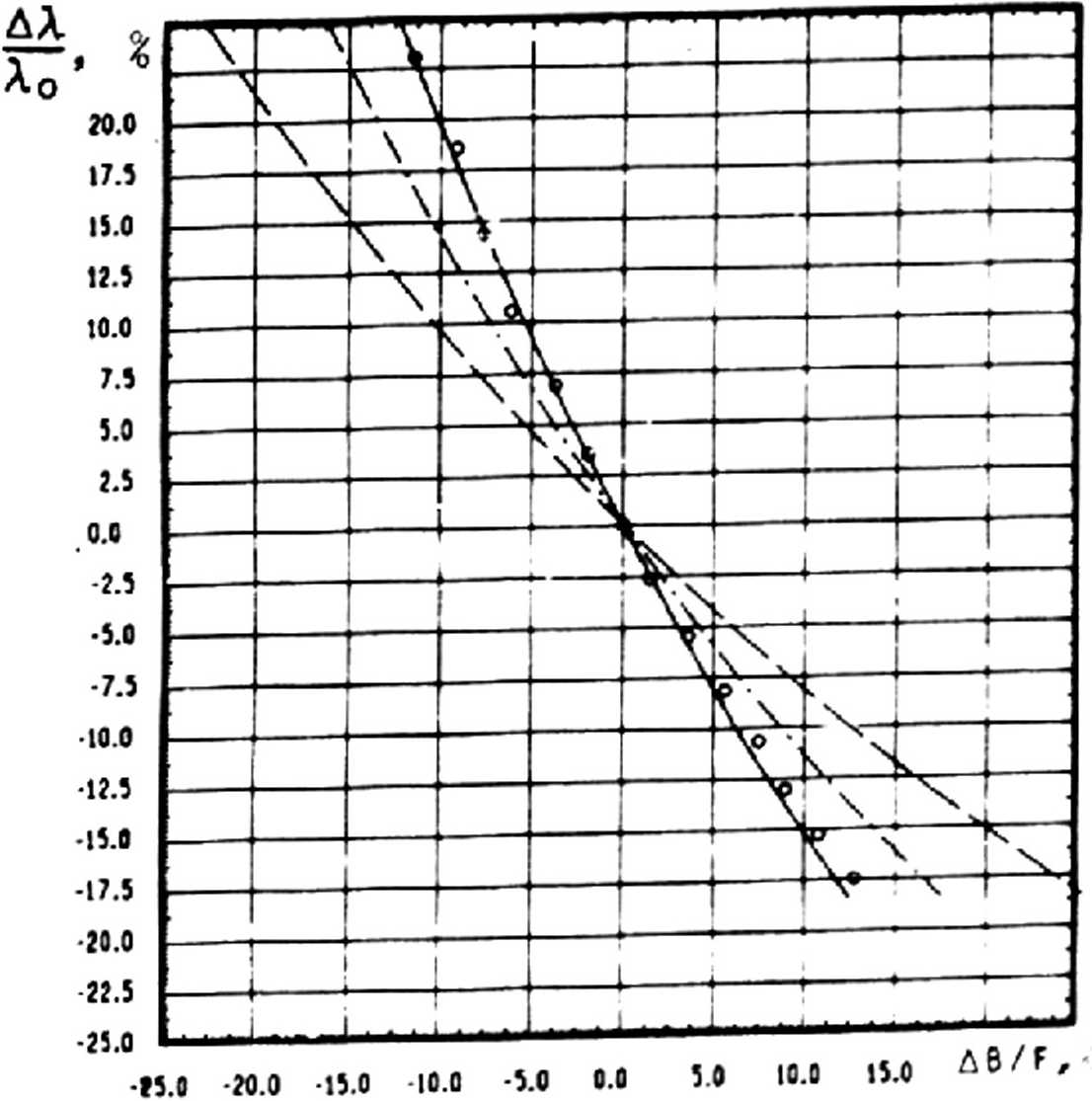
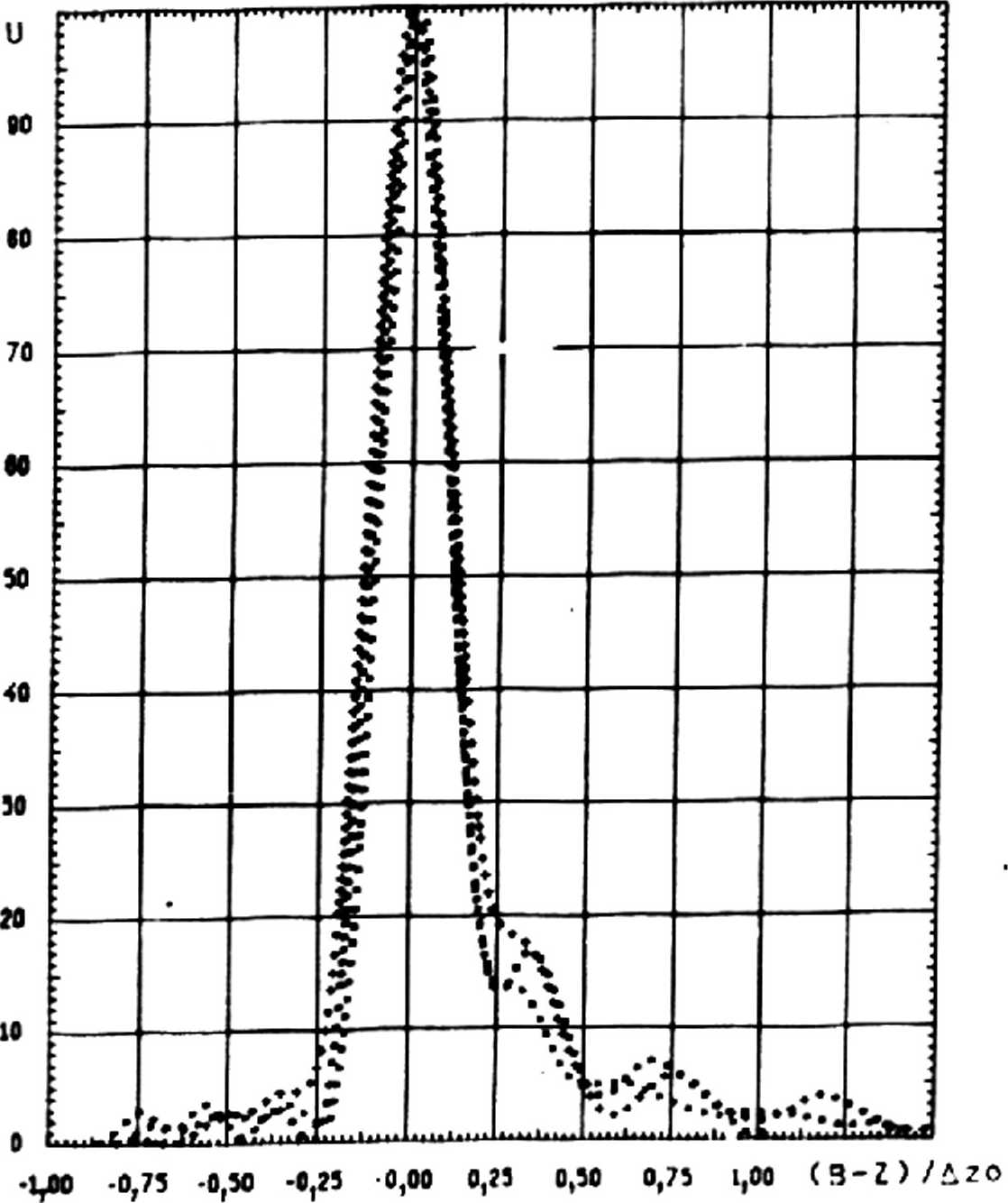
Q = [

X

X(Q) = 1 ♦ (B-z)/Q.

Примем, что образующая поверхности дифракционного элемента описывается корнем квадратным из квадратного трехчлена:

г = [az2 + 0z + с]1/я .                                                          (8)

Эта форма представления удобна потому, что уравнение (8) описывает:

• -    эллипс при ас - 8^а/4 <0 , а<0;

• -    конус при р = с =0, а>0;

• -    гиперболу при ас - З^а/4 <0, а>0;

• -    параболу при a = с =0, 0^0.

Вычисляя элемент площади по (6)z с учетом (8) имеем:

dS = 0z5[(2r)2 + (2az ♦ pJ^Vadedz.

Подставляя полученное выражение в (7), получаем окончательное выражение для интеграла Френеля-Кирхгофа, описывающего дифракцию скалярной волны на дифракционном квазиоптическом объективе, выполненном на поверхности вращения второго порядка. Для сокращения времени счета вычисление (7) проводилось по алгоритму, предложенному в работе [3] , на разработанной интерактивной системе проектирования компьютерной оптики [9]•

Экспериментальные исследования проводились в четырехмиллиметровом диапазоне длин волн; в качестве источника излучения использо.вались стандартные генераторы типа Г4-142, приемником служил кремниевый диод типа Д-407, нагруженный на открытый конец четырехмиллиметрового волновода.

Измерения проводились на оптической скамье, где были приняты меры по устранению переотражения излучения от металлических частей экспериментальной устано-ки. Ее схема и методика проведения экспериментальных исследований подробно описаны в работе [9] » погрешность эксперимента составляла - 7% .

Дифракционный объектив был выполнен на конической поверхности и изготовлен на станках с числовым программным управлением из оптического полистирола, имеющего следующие оптические константы: показатель преломления n=1.59z показатель поглощения к~10-э. Фазовый профиль наносился на внутреннюю поверхность полого конуса с углом расствора а=70 градусов, высота фазовой ступеньки определялась по выражению:

«п-П

Радиусы зон Френеля определялись в соответствии с выражением

nA о

2 tg а +

+ 4 В + nA)]1/ = ,

хп =

Номинальная длина волны составляла А_О=4.6 мм, апертура D/A_o=44, задний отрезок B*D. Максимальная стрелка прогиба поверхности ЗДК составляла <х>/А_о=32.

Внешний вид дифракционного объектива приведен на рис. 3.

Рис. 3. Внешний вид ЭДК на конической поверхности

Результаты исследований

Распределение интенсивности поля вдоль оптической оси в области фокуса рассматриваемого элемента ЭДК для различных длин волн СВЧ излучения приведено на рис. 4. По оси абсцисс отложено относительное расстояние вдоль оптической оси в единицах продольного разрешения для эквивалентной зонной пластины.

Анализ приведенных результатов показывает следующее:

• -    полуширина распределения интенсивности поля вдоль оптической оси Сна полу-высоте) для конической ЭДК с приведенными выше параметрами в 2 раза уже, чем для эквивалентной зонной пластины (при падении излучения со стороны вершины ЭДК);

• -    при падении излучения со стороны основания ЭДК ширина распределения интенсивности поля вдоль оптической оси примерно в -2,5 раза больше, чем для экви валентной ЗП;

• -    Форма рассматриваемого* распределения, представленная в относительных величинах, изменяется мало (~23) в диапазоне длин волн, отличных от расчетной не менее чем на ±133;

• -    при уменьшении длины волны СВЧ излучения от расчетной возрастает интенсивность первого бокового максимума, расположенного дальше от ЗП относительно максимума распределения. При этом величина возрастания его относительной интенсивности примерно совпадает с величиной расстройки длины волны излучения.

При падении на элемент ЭДК плоской электромагнитной волны оценку продольного разрешения (5) можно записать как

± <Х">'                                                            (9)

где д3~  - продольное разрешение эквивалентной ЗП;

<хп> - средняя величина стрелки прогиба поверхности ЭДК.

Таким образом, основной вывод заключается в том, что выбором стрелки прогиба поверхности ЭДК и ее ориентацией в пространстве можно регулировать продольное разрешение дифракционного объектива; при этом имеет место инвариант продольного разрешения (9).

Рассмотрим следующую характеристику элемента ЭДК - его частотные свойства. На рис. 5 приведены зависимости величины заднего отрезка от относительной расстройки длины волны СВЧ излучения, падающего на его вершину. По оси ординат отложена относительная расстройка длины волны излучения, по оси абсцисс - относительное смещение области фокусировки вдоль оптической оси (сплошная линия -теоретическая кривая, кружочки - экспериментальные данные, штриховая линия -зависимость для эквивалентной зонной пластины, штрихпунктирная - для ЗП с измененной величиной заднего отрезка В* = В - <х>/2, где <х> - стрелка прогиба поверхности конического элемента ЭДК.

Рис. 5. Зависимость изменения фокусного расстояния от относительной расстройки длины волны:

теория

Рис. 4. Распределение интенсивности поля вдоль оптической оси в области фокуса ЭДК при падении излучения со стороны его вершины

ЗП

ЗГ с 9’-0-<х>/2

Анализ приведенных частотных зависимостей конического ЭДК и зонных пластин показывает следующее:

• -    скорость перестройки положения области фокусировки вдоль оптической оси для конического объектива в 1.5“1.6 раза больше, чем для эквивалентной зонной пластины;

• -    частотные свойства конического ЭДК совпадают с таковыми для зонной пластины, имеющей величину заднего отрезка конического объектива, уменьшенной на зна-

• чение стрелки прогиба его поверхности, (Последнее также может быть использовано для целей моделирования частотных свойств конической ЭДК.)

Последнее утверждение следует из частотного инварианта рассматриваемого ЭДК, который с учетом (2) и хп«Уп можно записать как

В (X) » О , 5 с в +) (X) * В<-> (X)) , где

В<+\ В(-) - частотные свойства ЭДК при падении излучения со стороны основания и вершины его поверхности соответственно;

В(X) - частотные свойства эквивалентной ЗП.

Исследования поперечного разрешения рассматриваемого ЭДК показали, что во всем рабочем спектральном диапазоне он обеспечивает разрешение не хуже дифракционного предела.

Таким образом, в настоящей работе впервые установлены инварианты частотных свойств и продольного разрешения элементов дифракционной квазиоптики, выполненных на произвольной поверхности вращения второго порядка. Показано, что выбором Формы поверхности таких элементов и ее ориентацией в пространстве относительно положения области фокусировки возможно управлять их фокусирующими и частотными свойствами. Это позволяет существенно расширить функциональные возможности дифракционной квазиоптики и тем самым значительно увеличить область ее возможного применения.