Инвариантный метод с асимметричной структурой построения эхокомпенсатора

Для решения проблемы «последней мили» используются многочисленные эхо-компенсаторы, принцип работы которых основан на моделировании параметров неизвестной системы. Такой принцип обработки информационных сигналов имеет ряд положительных и отрицательных сторон. Среди существенных отрицательных моментов работы подобных алгоритмов следует считать сложность их реализации в реальном масштабе времени при организации высокоскоростного дуплексного обмена, а также критичность их работы от корреляционных связей сигналов двух направлений.

Другим подходом в построении адаптивных эхо-ком-пенсаторов является использование инвариантных соотношений, являющихся неизменными при изменении геометрических координат в выбранном пространстве.

Инвариантные методы построения эхо-компенсаторов позволили избавиться от серьезного недостатка работы классических эхо-компенсаторов. Технические характеристики инвариантных эхо-компенсаторов не зависят от корреляционных связей сигналов двух направлений.

Однако в подобных эхо-компенсаторах используются зеркально симметричные структуры и необходимо применять особые меры для устойчивой работы рекурсивных цепей.

Данная работа является продолжением исследования в области построения инвариантных эхо-компенсаторов и направлена на синтез устойчивых инвариантных алгоритмов эхо-компенсации.

Постановка задачи . Имеется канал связи, отвечающий условию стационарности. Полоса пропускания канала связи ограничена нижней и верхней частотами. В качестве эхо-компенсатора используются инвариантные ал- горитмы эхо-компенсации, включающие зеркально-симметричные структуры. Необходимо синтезировать инвариантный алгоритм эхо-компенсации, не требующей дополнительных мер к устойчивой работе.

Теория . В работах [1; 2] приведены алгоритмы функционирования инвариантных эхо-компенсаторв с защитным и без защитного временных интервалов. Суть этих алгоритмов основана на использовании инвариантного соотношения энергетических спектров. При синтезе инвариантного эхо-компенсатора с защитным временным интервалом использовался инвариант, равный [1]

S ( z ) = П( z ) S - 1 ( z )   П - 1 ( z )’

где S , . ( z ), S,. - 1 ( z ) - z- изображение сигнала передачи соответственно на -м и ( – 1) блоках обработки; П , ( z ), П , - 1 ( z ) - z -изображение эхо-сигнала соответственно на -м и ( – 1) блоках обработки.

При построении инвариантного алгоритма работы эхо-компенсатора без защитного временного интервала параллельно передающему устройству включен дополнительный, физически реализуемый четырехполюсник [2]. В работе [3] доказано, что если на входы параллельно работающих четырехполюсников подается одинаковое возмущающее воздействие, то отношение энергетических спектров, вычисленных на соседних блоках обработки на выходах указанных выше четырехполюсников, есть величина постоянная, т. е. является инвариантом.

В первом и втором случаях сама структура эхо-ком-пенсатора, включенного перед приемным устройством, представляет собой зеркально симметричный четырехполюсник с передаточной характеристикой, равной

Математика, механика, информатика

H ( z ) =

1 - M_t ( z ) • z

1 - M i ( z ) • с • z ¹ ’

где M i ( z ) - z -изображение управляющего коэффициента на i -м блоке обработки; c < 1 - дополнительный атте

нюатор, включенный в рекурсивную цепь.

Если реализуется алгоритм эхо-компенсации с защитным временным интервалом, то M i - ( z ) равно

Технические характеристики . Для определения величины собственного шума необходимо знать импульсные реакции первого и второго цифровых фильтров. Импульсные реакции h 1 (nT ) и h ₂( nT ) необходимо определить при единичном сигнале управления ( M i ( z ) = 1). При других значениях сигнала управления импульсные реакции линейно изменяются.

M i ( z )

= S i ( z ) S i - 1 ( z ) '

Если реализован алгоритм эхо -компенсации без защитного временного интервала, то M i ( z ) равен:

m , ( z )= Qirzr; •             (4)

ЙД z z)

В выражениях (3) и (4) приняты следующие обозначе-

ния:

M i ( z ) - z -изображение управляющего коэффициента на i -м блоке обработки;

S i ( z ) - z -изображение сигнала передачи на i -м блоке обработки;

Q i (z ) - z -изображение сигнала, наблюдаемого на выходе дополнительного четырехполюсника, если на его вход подан сигнал S i ( z ) .

Из теории цифровой фильтрации известно, что физически реализуемый цифровой фильтр по выражению (2) должен иметь полюс, лежащий внутри единичного круга на z плоскости [4]. Отсюда следует, что

M( z ) <  1.                  (5)

Для достижения условия (5), в работах [1; 2] использовались нормирующие четырехполюсники, которые были включены на информационные и управляющие входы

самого эхо-компенсатора.

Однако устойчивость рекурсивной структуры любого цифрового фильтра можно обеспечить путем преобразования ее в нерекурсивную структуру.

Преобразуем передаточную рекурсивную характеристику, описываемую выражением (2) в нерекурсивную

структуру:

1 - M i ( z ) • с • z

K - 1

= Z [ ^M-; ( z ) ]

j = ⁰

z

где M i ( z ) - z- изображение управляющего коэффициента на i -м блоке обработки; к - число сигналов во вновь

синтезированной нерекурсивной структуре цифрового фильтра.

Структура инвариантного эхо-компенсатора первого порядка, использующая в своей работе два нерекурсив-

ных цифровых фильтра приведена на рис. 1.

Впервые такое преобразование приведено в [5].

В первом цифровом фильтре производится компенсация эхо-сигналов. Наряду с компенсацией эхо-сигналов, в этом цифровом фильтре одновременно производится преобразования сигналов приема.

Во второй части синтезированной структуры произ-

водится восстановление сигнала приема.

Следует отметить, что синтезированная структура представляет собой однородный цифровой фильтр [4].

У двух каскадно-соединенных нерекурсивных цифровых фильтров фазочастотная характеристика будет линейной [4].

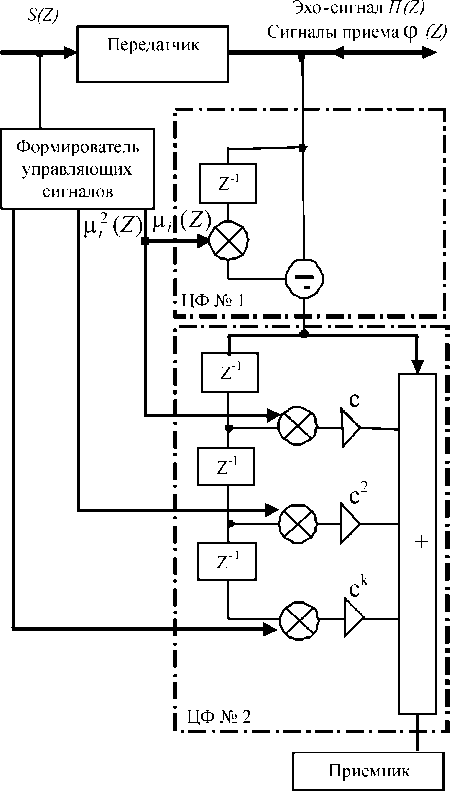
Рис. 1. Инверторный ассиметричный эхо-компенсатор

Тогда h1( nT) = { 1 -1}, h2(nT) = { 1, c, c2,..., c}= cn.

Общая импульсная реакция всего эхо-компенсатора определяется сверткой :

h _E ( nT ) = h 1 ( nT ) • h ₂ ( nT ) = cⁿ - c^{n - 1},         (7)

где с < 1 - коэффициент передачи аттенюатора.

Мощность собственных шумов определяется известным соотношением д2 K- 1             д2 K - 1K- 1

»² = 7т X h Й nT ) + ^ XX h j nT ),   (8)

¹² n = 0               ¹² j = 0 n = 0

где A - шаг квантования в эхо-компенсаторе; А ₀ - шаг квантования входного информационного слова; h _z ( nT ) -определена выражением (7); h _X j ( nT ) - импульсная реакция от j -го источника шума ( j' -й ветви) до выхода; K - число отводов в ЦФ2.

Для упрощения расчетов будем полагать что А ₀ = А , h _у ( nT ) = h _у j ( nT ). Тогда величина собственного шума определяется как

Л 2

о2 = — (K +1) у hУ( nT) = д 1       K -Г 0

_ ( K ⁺ 1) у ( c n - c n - 1 ) 2 .

Но

K -1                     K -1           1             1      2k k—A

У ( c n - c n "  1 ) 2 = у c²ⁿ (1 - -)² = (1 - -)² ■ c y-- .

n = 0                  n = 0         c           cc

Тогда общая формула расчета величины собственного шума при указанных выше ограничениях будет равна 22

о2 =_°( K +1) ■ (1 - 1)2 ■ £^.(10)

• 12             c c - 1

Таким образом, синтезирован инвариантный асимметричный эхо-компенсатор и найдено аналитическое выражение для расчета собственных шумов.

Синтезированный алгоритм может быть широко применен в телекоммуникационном оборудовании для борьбы с эхо-сигналом.