Inverse optimum safety factor method for reliability-based topology optimization applied to free vibrated structures
Автор: Kharmanda Ghias, Antypas Imad R., Dyachenko Alexey G.
Журнал: Инженерные технологии и системы @vestnik-mrsu
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 1, 2019 года.
Бесплатный доступ
Introduction. The classical topology optimization leads to a prediction of the structural type and overall layout, and gives a rough description of the shape of the outer as well as inner boundaries of the structure. However, the probabilistic topology optimization (or reliability-based topology optimization) model leads to several reliability-based topologies with high performance levels. The objective of this work is to provide an efficient tool to integrate the reliability-based topology optimization model into free vibrated structure. Materials and Methods. The developed tool is called inverse optimum safety method. When dealing with modal analysis, the choice of optimization domain is highly important in order to be able to eliminate material taking account of the constraints of fabrication and without affecting the structure function. This way the randomness can be applied on certain boundary parameters. Results. Numerical applications on free vibrated structures are presented to show the efficiency of the developed strategy. When considering a required reliability level, the resulting topology represents a different topology relative to the deterministic resulting one. Discussion and Conclusion. In addition to its simplified implementation, the developed inverse optimum safety factor strategy can be considered as a generative tool to provide the designer with several solutions for free vibrated structures with different performance levels.
Deterministic topology optimization, reliability-based topology optimization, modal analysis, optimum safety factor, optimization domain
Короткий адрес: https://sciup.org/147220610
IDR: 147220610 | УДК: 515.1:004.9 | DOI: 10.15507/2658-4123.029.201901.008-019
Текст научной статьи Inverse optimum safety factor method for reliability-based topology optimization applied to free vibrated structures
Topology optimization attempts to answer one of the first questions concerning the nature of the structure to fulfill the necessary technical specifications. The topology problem would then consist of determining the structure’s general characteristics, and the goal of topology
Сomputer science, computer engineering and management
optimization would be to make that initial choice as automatically as possible [1]. In addition, when using topology optimization concepts, both macroscopic structures and microscopic materials can be found. In other word, we determine not only the optimal spatial material layout distribution at the macroscopic structural scale, but also 9
the optimal local use of the cellular material at the microscopic scale1.
In the literature, two main models of topology optimization can be distinguished: deterministic model and probabilistic (or reliability-based) one. In Deterministic Topology Optimization (DTO), a single solution for a given domain can be searched2. However, the ReliabilityBased Topology Optimization (RBTO) model developed in this paper can lead to several solutions with different advantages. It enables us to choose the best solution to fulfill the technical specifications. The structural weight of the resulting topologies obtained by this model is reduced in comparison to the DTO model. In addition, when using the RBTO model, the structure obtained is more reliable compared to deterministic topology for the same weight levels3. Two points of view are presented for the development of this model: topology optimization and reliability analysis. A literature review is established in the next section, to show the different advantages of the RBTO model.
Literature Review
The main difference between deterministic topology optimization and reliability-based topology optimization is to consider the hazards about the parameters having important roles for optimal topology. The main idea of the RBTO is based on the Reliability-Based Design Optimization (RBDO). In a RBDO problem, the uncertainties regarding the sizing variables are taken into account in order to ensure greater reliability of the proposed
Том 29, № 1. 2019
solution. However, the RBTO seeks to provide designers with several solutions that have several reliability levels. This way the designer can select best solution. In the Reliability-Based Design Optimization (RBDO), several methods have been developed. The different developments can be classified in two points of view:
From point of view “topology optimization”, Kharmanda and Olhoff 4 have elaborated an RBTO model with object of providing the designer with several reliability-based structures however in the classical topology optimization, the designer produces only one deterministic topology. It has been shown the importance of the RBTO model yields structures that are more reliable than those produced by deterministic topology optimization (for the same weight, see also5 [2; 3]). In the RBTO model reliability constraints have been introduced into deterministic topology optimization problem. The initial sensitivity analysis is used to identify random variables which have significant effect on the objective function and the limit state function used is a linear combination of the random variables. Therefore, the proposed approach is a heuristic strategy that aims to reduce mass while improving the reliability level of the structure without greatly increasing its weight. But the limit state function used by them was not based on failure criteria for the structure. This formulation considered uncertainty with respect to geometrical dimension and applied load only. Also their reliability analysis seems to be independent of the boundary and loading condition, so
Vol. 29, no. 1. 2019 their results showed similar values for the uncertain variables for different structures. Next, Patel and Choi [4] used probabilistic neural networks in the case of highly nonlinear or disjoint failure domain problems. This strategy has been efficiently applied on different truss structures. Recently, Wan et al. [5] developed a non-probabilistic reliability-based topology optimization method for detailed design of continuum structures, in which the unknown but bounded uncertainties (UBB) existing in material and external loads are considered simultaneously. Their results show that considering the UBB uncertainty effects during the whole procedure of topology optimization may have a significant influence on the final structural configurations.
From a point of view “reliability analysis”, the classical topology optimization is formulated as finding the stiffest structural layout with a volume constraint. Here, the feasibility of volume constraint is not critical in structural design problems. It is more important to consider the variations of the stiffness under uncertainties. To maintain the robustness of stiffness in the topology design, Bae and Wang [6] formulated the topology design optimization as volume minimization problem with a displacement constraint and applied the RBDO technique. They minimize the structural volume subject to linear limit state function. In the research of, the extension of the work of Bae and Wang for the geometrically non linear problems is studied or reformulated to avoid repetition. They minimize the structural volume subject to a nonlinear limit state function. Next, Patel et al. [7] have developed the Hybrid Cellular Automaton (HCA) method for structural synthesis of continuum material where the state of each cell is defined by both density and strain energy. In6, a decoupled RBDO approach is employed such that the topology optimization is separate from the reliability analysis [7] showed the use of RBTO using the gradient free Hybrid Cellular Automata (HCA) method. Their formulation incorporates uncertainty with respect to material property also. They considered limit state function based on failure modes on the output displacements. Eom et al. [8] performed the RBTO model using bi-directional evolutionary structural optimization and the standard response surface method. Jalalpour and Tootkaboni [9] developed a computationally method for reliability-based topology optimization for continuum domains under material properties uncertainty.
Comparing both different points of view, RBTO methods from a point of view “reliability analysis” are inherently computationally expensive because of additional required system analysis associate with RBDO since a large number of design variables are associated with continuum topology optimization problems7.
So the point of view “topology optimization” seems to be interesting for topology designers because it provides several reliability-based structures relative the reliability index changes. It leads to different layout structures while the developments from a point of view “reliability analysis” leads to same layout structures with different densities that have no sense for the following optimization stages [10].
To perform the RBTO problems, different RBDO techniques can be used since we deal with different problem definition or philosophy. Several RBDO methods have been developed regarding to their use8; 9 [11]. For example, the OSF method as an efficient RBDO tool, has been simply implemented by performing two main stages [12]. The first stage is to find the failure point (design point) using a simple optimization process while the second stage consists of using the OSF formulations to find the optimum solution. In this work, for the RBTO model, the developed Inverse Optimum Safety (IOSF) method consists of first finding the configuration using Deterministic Topology Optimization (DTO). Next, the OSF formulations [12] are used with inverse derivative signs in order to provide several reliability-based topologies. The resulting topologies are controlled by a given design space (loading, material, geometry, meshing…). In the modal analysis, there is no applied loads. So the integration of topology optimization into free vibrated structures may lead to unrealistic topologies. Therefore, the choice of optimization domain is highly important in order to be able to eliminate material taking account of the constraints of fabrication and without affecting the structure function. For this purpose, several choices are carried out to demonstrate the importance of optimization domains relative to the static studies [3] where the used boundary conditions can lead to admissible topologies.
Materials and Methods
Deterministic Topology Optimization The topology optimization problem relates to the minimization of the strain energy, subject to the limitation of the structural volume10. All the loading parameters and material properties are considered deterministic. The topology optimization problem is to minimize the compliance, subject to a target percentage value of volume f t . This problem can be mathematically written as follows:
min : Comp st.: - £ f,, (1)
‘ where Comp is the compliance considering the material densities in each element as optimization variables that belong to the interval [0, 1]. V0 and V are the initial and current volume values. Formulation (1) is a basic form and can be used with several topology optimization methods such as SIMP (Solid Isotropic Microstructure with Penalty), homogenization approach, ... [13; 14].
Reliability-Based Topology Optimization
In deterministic structural optimization, the designer aims to reduce the construction cost without taking into account the effects of uncertainties concerning materials, geometry and loading. This way, the resulting optimal configurations may represent a lower reliability level and then leads to higher failure rate. The balance between the cost minimization and the reliability maximization is a great challenge for the designer. The importance of the reliability criteria on the deterministic design optimization is to improve the reliability level in the system without largely increasing its weight. Thus, when integrating the reliability concept into the sizing and shape optimization, the model is called Reliability-Based Design Optimization (RBDO), which allows us to design structures, which satisfy economy and safety requirements. But when coupling the reliability analysis with the topology optimization being considered non-quantitative of nature. The coupling model is called Reliability-Based Topology Optimization (RBTO) [15]. The purpose of the Reliability-Based Topology Optimization (RBTO) is to consider some uncertainties of the geometry or the loading of the structure, by introducing the reliability criteria in the optimization procedure. This integration takes into account the randomness of the applied loads and the geometry description. The RBTO problem is generally written as:
min : Comp st.: в ^ P, and : — < f,
t,
V 0
where β and βt are the reliability index of the system and the target reliability index, respectively (for more information about reliability methods, see11 [16]). The integration of reliability analysis into the topology optimization has been carried out by performing two decoupled problems for static studies [2]. However, in this work, an efficient method called Inverse Optimum Safety method, is developed and applied to free vibrated structures considering the design domain uncertainty.
U = e t
n
∂ G
∂yi
∂ G
1 dy j
, i = 1,..., n , (3)
where the sign of ± depends on the sign of the derivative of the limit state function with respect to random vector yi , i. e.,
e-G > о dУг
i
Considering that the random variable vector follows the normal distribution law, the safety factor can be written as fol-lows12 [16]:
Sf = 1 + 7 . • u i , i = 1 ,...,n , (5) where the variance coefficient γi relating the mean mi and standard-deviation σi equals to: γi = σi / mi .
However, the idea of the developed IOSF is to find a resulting deterministic topology Py * considered as a failure point, and next we seek a reliability-based topology Px * that should be more reliable than the first solution Py * as well as should respect a required reliability level βt . So the failure point Py * is found by a DTO procedure and the reliability-based topologies Px * are found using the OSF formulations but with inverse derivative signs (formulation 4). This strategy generates several reliability-based topologies according to the reliability index values. The generation of several topologies is controlled by a sensitivity analysis being an efficient indicator to find the role of each parameter.
Results
In this section, the topology optimization is applied to a 2D cantilever beam (dimensions: 200 × 50 mm) to find the best distribution of material. The material in this beam is steel, which has a Young’s modulus E = 200 000 MPa and a Poisson’s ratio equal to: v = 0.3. The density of the material is ρ = 7.190 × 10 Kg/mm.The behavior of the material is linear elastic isotropic. The objective is to perform topology optimization to obtain the best distribution of the materials. The topology optimization problem is to minimize the compliance of the structure, subject to the volume fraction 50 %. To carry out topology optimization, the meshing model is constructed using the nonlinear element (PLANE82 – 8-node) and the used method is the Optimality Criteria (OC) implemented in ANSYS Software.
When considering the modal studies, the choice of optimization domain is very important in order to be able to eliminate material taking account of the constraints of fabrication and without affecting the function of the resulting cantilever beam.
-
11 Kharmanda G., Antypas I. Integration of reliability and optimization concepts into composite yarns. In: 10th International Scientific-Practical Conference of Current Status and Prospects of Agricultural Engineering, “INTERAGROMASH-2017”. Rostov-on-Don: DSTU Publ. Centre; 2017. p. 174-176.
-
12 Kharmanda G., El-Hami A. Biomechanics optimization, uncertainties and reliability. ISTE–Wiley, 2017. Available at: http://ebook-dl.com/book/8163
For this purpose, we optimize several cases in order to first demonstrate the importance of the initial design domain and then show the advantages and disadvantages of each model.
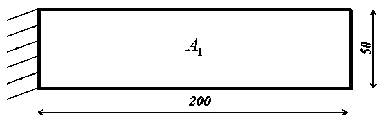
Fig. 1, a‒b respectively show the geometric model of the studied beam and the resulting topology, considering the entire geometry as an optimization domain A 1 (i. e. the domain to be optimized).
Том 29, № 1. 2019
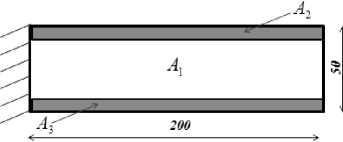
Fig. 2, a shows the geometric model of the studied beam, considering middle part as the optimization domain A 1 and the upper and lower parts as the domain not to be optimized ( A 2 and A 3). Fig. 2, b shows the corresponding resulting topology.
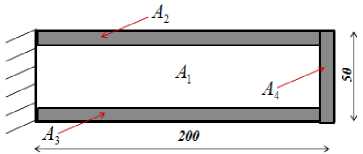
Fig. 3 shows the geometric model of the studied beam, considering inner part as the optimization domain A 1, the upper,
a)

b)
F i g. 1. Configurations of model 1 when considering deterministic topology optimization:
-
a) a cantilever beam with a single optimized area; b) resulting topology
Р и с. 1. Конфигурация модели 1 при рассмотрении оптимизации детерминированной топологии: a) консольная балка с одной оптимизированной областью;
-
b) результирующая топология
a)
b)
F i g. 2. Configurations of model 2 when considering deterministic topology optimization:
-
a) a cantilever beam with double non-optimized areas; b) resulting topology
Р и с. 2. Конфигурация модели 2 при рассмотрении оптимизации детерминированной топологии: a) консольная балка с двойными неоптимизированными областями;
-
b) результирующая топология
a)

b)
F i g. 3. Configurations of model 3 when considering deterministic topology optimization: a) a cantilever beam with triple non-optimized areas; b) resulting deterministic topology optimization
Р и с. 3. Конфигурация модели 3 при рассмотрении оптимизации детерминированной топологии: a) консольная балка с тройными неоптимизированными областями; b) результирующая оптимизация детерминированной топологии lower and lateral parts as the domain not to be optimized (A2, A3 and A4).
Here, the dimensions (x1, x2, x3) of non-optimized domain of the third model are considered as random variables (see fig. 4, a). At the initial point, these variables equal to: 5 mm. The target reliability index is equal to βt = 3 and that the proportion of the standard deviations compared to the average values is equal to13. Fig. 3, b and 4, b show the corresponding resulting DTO and RBTO configurations, respectively.

-
a) b)
F i g. 4. Configurations of model 3 when considering reliability-based topology optimization: a) initial design with 3 random variables; b) resulting reliability-based topology optimization Р и с. 4. Конфигурация модели 3 при рассмотрении оптимизации топологии на основе надежности: а) первоначальная конструкция с 3 случайными величинами;
-
b) результирующая оптимизация топологии на основе надежности
T a b l e 1
Т а б л и ц а 1
Reliability-based topology optimization results
Результаты оптимизации топологии на основе надежности
|
Parameters / Параметры |
Thickness of lower part x 1 / Толщина нижней части x 1 |
Thickness of lateral part x 2 / Толщина боковой части x 2 |
Thickness of upper part x 3 / Толщина верхней части x 3 |
|
Failure point P y / Точка отказа P y |
5.00 |
5.00 |
5.00 |
|
Compliance Comp / Соответствие Comp |
1.37700 |
1.37766 |
1.37766 |
|
Compliance sensitivity d C / d y , / Соблюдение чувствительности d C / d y |
–0.020 |
–0.018 |
–0.025 |
|
Normalized vector u* / Нормализованный вектор ui |
1.683 |
1.626 |
1.877 |
|
Optimum safety factors S f / Оптимальные факторы безопасности S fi |
1.420 |
1.407 |
1.469 |
|
Optimum point P X / Оптимальная точка P X |
7.10 |
7.03 |
7.35 |
Table 1 presents the different parameters concerning the failure point P y and the optimum point P x considering the target reliability index βt = 3.
At the failure point Py * , the normalized vector u i is evaluated according to formulation (3) considering the central finite difference technique to evaluate the required derivatives of the compliance d C / d y i 14 . The safety factors S f. are next computed according to formulation (5) and the corresponding reliability-based topology is finally evaluated at the optimum point Px * .
Discussion and Conclusion
According to our previous [2; 3], when considering a static case, the loading and the fixation can control the external geometrical boundaries However, when considering the modal studies, the choice of optimization domain is very important in order to be able to eliminate material taking account of the constraints of fabrication and without affecting the function of the resulting structures. Three models with different optimization domains are studied to show the effect of the optimization domain choice.
For the first model, when considering the entire geometry as an optimization domain, the resulting topology changes totally the external geometry and then affects its function. Fig. 1, b shows that the cantilever beam length is reduced which can totally change the detailed design stage. Therefore, the initial design domain should be modified to attend the design objectives. For second model, the upper and lower parts are considered as non-optimized domains. This way the resulting topology is better than the first model but some other failure scenarios can occur at the right region. However, in the
Том 29, № 1. 2019
third model, all free boundaries are considered as non-optimized domains. The resulting topology will not affect beam function. Here, the DTO algorithm leads to a single topology considering a given initial design space while the RBTO algorithm leads two several topologies relative to the reliability index values.
The main different between the IOSF and OSF method is to invert the sign of the derivatives is inverted. Here, the mean values are considered to be the failure point Py * , and the objective is to increase the reliability level starting from this point. The resulting DTO configuration leads to weak sections (fig. 3, b) and meets difficult fabrication constraints while the RBTO configuration (fig. 4, b) is much more reliable than that produced by DTO.
In general, the choice of the initial domain depends on the designer experience and may lead to several failure scenarios. A reliability concept can be integrated during the optimization process in order to control the resulting topology performance and to generate several reliability-based topologies. In this problem, when applying the IOSF method to obtain a layout which respects a required reliability level, a different topology is obtained. The advantage of this strategy is to produce different topology with additional computing cost regarding the reliability stage.
Thus, reliability-based topology optimization is able to generate multiple topologies, giving the designer a range of solutions by adding certain reliability constraints. The efficiency of the developed IOSF method is to perform the RBTO in a single loop relative to the previous method proposed by [2] which also needs double loops.
14 Ibid.
Список литературы Inverse optimum safety factor method for reliability-based topology optimization applied to free vibrated structures
- Bendsee M. P., Kikuchi N. Generating optimal topologies in structural design using a homo-genization method // Computer Methods in Applied Mechanics and Engineering. 1988. Vol. 71, Issue 2. P. 197-224. DOI: 10.1016/0045-7825(88)90086-2
- Reliability-based topology optimization / G. Kharmanda [et al.] // Structural and Multidisciplinary Optimization. 2004. Vol. 26, Issue 5. P. 295-307. DOI: 10.1007/s00158-003-0322-7
- Reliability-based topology optimization for different engineering applications / G. Kharmanda [et al.] // International Journal of CAD/CAM. 2007. Vol. 7, no. 1. P. 61-69. URL: https://www.research-gate.net/profile/Ghias_Kharmanda/publication/259383338_Reliability-Based_Topology_Optimization_ For_Different_Engineering_Applications/links/0a85e53c7adb1a24d6000000.pdf
- Patel J., Choi S.-K Classification approach for reliability-based topology optimization using probabilistic neural networks // Structural and Multidisciplinary Optimization. 2012. Vol. 45, Issue 4. P. 529-543. DOI: 10.1007/s00158-011-0711-2
- A novel method of non-probabilistic reliability-based topology optimization corresponding to continuum structures with unknown but bounded uncertainties / L. Wang [et al.] // Computer Methods in Applied Mechanics and Engineering. 2017. Vol. 326. P. 573-595. DOI: 10.1016/j.cma.2017.08.023
- Bae K., Wang S. Reliability-based topology optimization // 9th AIAA/ISSMO Symposium on Multi-disciplinary Analysis and Optimization. 2002. AIAA 2002-5542.
- DOI: 10.2514/6.2002-5542
- Reliability based topology optimization using the hybrid cellular automaton method / N. M. Patel [et al.] // 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. 2005. AIAA 2005-2134.
- DOI: 10.2514/6.2005-2134
- Reliability-based topology optimization using a standard response surface method for three-dimensional structures / Y.-S. Eom [et al.] // Structural and Multidisciplinary Optimization. 2011. Vol. 43, Issue 2. P. 287-295.
- DOI: 10.1007/s00158-010-0569-8
- Jalalpour M., Tootkaboni M. An efficient approach to reliability-based topology optimization for continua under material uncertainty // Structural and Multidisciplinary Optimization. 2016. Vol. 53, Issue 4. P. 759-772.
- DOI: 10.1007/s00158-015-1360-7
- Kharmanda G. The safest point method as an efficient tool for reliability-based design optimization applied to free vibrated composite structures // Вестник Донского государственного технического университета. 2017. Т. 17, № 2 (89). С. 46-55.
- DOI: 10.23947/1992-5980-2017-17-2-46-55
- Reliability based design optimization for multiaxial fatigue damage analysis using robust hybrid method / A. Yaich [et al.] // Journal of Mechanics. 2018. Vol. 34, Issue 5. P. 551-566.
- DOI: 10.1017/jmech.2017.44
- Харманда М. Г., Антибас И. Р. Стратегия оптимизации проектирования надежности почвообрабатывающей техники с учетом параметрической неопределенности почвы // Вестник Донского государственного технического университета. 2016. Т. 16, № 2. С. 136-147.
- DOI: 10.12737/19690
- Bendsee M. P. Optimal shape design as a material distribution problem // Structural Optimization. 1989. Vol. 1, Issue 4. P. 193-202.
- DOI: 10.1007/BF01650949
- Bendsee M. P., Sigmund O. Material interpolation schemes in topology optimization // Archive ofApplied Mechanics. 1999. Vol. 69, Issue 9-10. P. 635-654.
- DOI: 10.1007/s004190050248
- Харманда М. Г., Антибас И. Р. Интеграция концепции надежности в проектирование почво-обрабатьшающих машин // Вестник Донского государственного технического университета. 2015. Т. 15, № 2. С. 22-31.
- DOI: 10.12737/11610
- Ibrahim M. H., Kharmanda G., Charki A. Reliability-based design optimization for fatigue damage analysis // The International Journal of Advanced Manufacturing Technology. 2015. Vol. 76, Issue 5-8. P. 1021-1030.
- DOI: 10.1007/s00170-014-6325-2


