Инверсия циркулярной поляризации в анизотропных оптических волокнах с крутильной акустической волной

Акустооптическое взаимодействие (АОВ) широко используется для динамического управления параметрами оптических пучков. В волоконной акустооптике для модуляции диэлектрической проницаемости волноводов используют все три семейства упругих колебаний цилиндра: продольные, изгибные и крутильные [1, 2]. Продольные аксиально-симметричные моды не обеспечивают непосредственного взаимодействия оптических мод между собой, но находят применение в модуляции уже имеющейся в волокне брэгговской решетки. Такая комбинация стационарной и нестационарной волоконных решеток позволяет управлять пропусканием (отражением) пучка на боковых относительно несущей длинах волн [3, 4]. Изгибные акустические волны обеспечивают такое преобразование мод волокна, при котором происходит изменение их азимутальных чисел совместно со сдвигом частоты оптического излучения [5, 6]. На основе волокон с изгибными акустическими волнами создано множество полностью волоконных устройств для динамического управления пучками: переключатели мод и преобразователи частоты [7, 8], управляемые фильтры [9, 10] и ответвители [11, 12] и т.д. Обширные недавние исследования показывают, что такие волокна способны эффективно генерировать и модулировать топологически заряженные [13, 14] и цилиндрические векторные [15, 16] пучки. В свою очередь, крутильные акустические волны обеспечивают резонансное АОВ собственных ортогонально линейно-поляризованных мод анизотропного волокна. Так, в пионерской работе 1991 года [17] была экспериментально продемонстрирована конверсия поляризационных мод анизотропного волокна с эффективностью 6%. В последующие годы удалось продемонстрировать высокоэффективное преобразование мод в стандартных [18] и в фотонно-кристаллических [19] волокнах с сильной линейной анизотропией. Крутильные акустические волны нашли применение в устройствах генерации и фильтрации особым образом поляризованных пучков, а также в оптоволоконных преобразователях частоты [20, 21].

Несмотря на значительный прогресс в изучении АОВ в анизотропных волокнах с крутильными акустическими модами, внимание исследователей было сосредоточено на качественном описании экспериментально наблюдаемых преобразований мод посредством теории связанных мод [22]. Альтернативный подход заключается в установлении структуры собственных мод и их постоянных распространения посредством применения теории возмущений к волновому уравнению. Установленная модовая структура значительно упрощает последующее изучение эволюции произвольно-поляризованных мод, поскольку решение соответствующей краевой задачи сводится к решению простой системы линейных уравнений и не требует повторного решения исходных дифференциальных уравнений. Кроме того, такой подход имеет несомненное преимущество в возможности описания трансформации мод в окрестности соответствующего акустооптического резонанса.

Таким образом, целью данной работы является построение последовательной модели АОВ в анизотропных циркулярных волокнах с бегущей крутильной акустической волной основного порядка, определение структуры резонансных мод и их спектра постоянных распространения. Это позволит детально описать экспериментально наблюдаемое преобразование линейно-поляризованных LP 0 -мод. Кроме того, впервые будет изучена трансформация циркулярно-поляризованной LP 0 -моды, переносящей спиновый угловой момент.

1. Модель и моды циркулярного анизотропного волокна с крутильной акустической волной основного порядка

Диэлектрическая проницаемость циркулярного изотропного волокна описывается следующим выражением [23]:

s IF ( r ) = s co [1 - 2 Л f ( r )],                              (1)

с бегущей крутильной акустической волной основного порядка может быть записана в виде:

s ( r , ф , z , t ) = s AF ( r ) + 5s p ( r , ф , z , t ) + 5s b ( z , t ).        (4)

Здесь второе слагаемое получено из симметричной части тензора фотоупругости и имеет вид:

5s p ( r , ф , z , t ) = s 2o C 0 Krp 44 x
' 0      0     - sin ф^	(5) ,
x sin( Kz -Q t )   0      0 cos ф ч- sin ф cos ф 0 у

где p 44 – соответствующий элемент тензора фотоупругости. Последнее слагаемое вида

ˆ

^5s b ^{( z} , t ) = ^{2 С} 0 ^5s AN

( 0

cos( Kz - Q t ) 1

0 "

⁰ J

где Л = ( s _co - s cl )/2 s _co - высота профиля диэлектрической проницаемости, s _co и s cl - значения проницаемо-стей сердцевины и оболочки волокна соответственно, f ( r )-функция профиля. Влияние линейной анизотропии материала волокна с фиксированной ориентацией осей учитывается следующим преобразованием [24]:

s af ( r ) = diag( s x , s _y , s _y )[1 - 2 Л f ( r )] « ~s if - 1 + 5s an ■ S ,

где введены обозначения s _co = (1/2)( s x + s _y ), 5s AN =(1/2)( s x - s y ) - параметры линейной анизотропии, 1 – единичная матрица размерности 3×3, Ŝ = diag (1, – 1,– 1).

С точки зрения теории упругости циркулярное оптическое волокно представляет собой упругий изотропный цилиндр некоторого радиуса a [1]. В экспериментально реализуемом длинноволновом приближении Ka << 1 решение волнового уравнения для упругой среды может быть выбрано в виде крутильной акустической волны основного порядка с единственной ненулевой ф компонентой вектора деформации [22]:

u _ф = C 0 r cos( Kz -Q t ). (3)

Здесь C ₀ - нормировочная константа, K и Q - постоянная распространения в z -направлении и угловая частота крутильной волны соответственно, использована цилиндрическая система координат ( r , j , z ).

Как было ранее показано [22], диэлектрическая проницаемость циркулярного анизотропного волокна

происходит из антисимметричной части тензора деформации [25] и учитывает эффект вращения оптически анизотропной среды под действием крутильной акустической волны.

Собственные моды волокна в присутствии крутильной акустической волны могут быть получены как решение векторного волнового уравнения:

2 — —                 ^         ^

V² E +— [ s ( r , Ф , z , t ) E ] = V ( divE ),               (7)

d t ²

где V = ( S / 5 x , 5 / 5 y , 5 / 5 z ), E - вектор напряженности электрического поля. Для производных по времени во втором слагаемом (7) справедлива оценка:

dE     — s К s co йE, dt

E ^d5s p к s 2 o C 0 Kr ₀ p 44 Q E ,                       (8)

d t

— к 5s anC0 QE, dt где й - частота оптического излучения, r0 - радиус сердцевины волокна. Несложно видеть, что для экспериментально реализуемых параметров Q / й <<1 производной по времени от диэлектрической проницаемости в волновом уравнении можно пренебречь. Правую часть уравнения (7) принято называть градиентным членом, данное слагаемое описывает эффект спин-орбитального взаимодействия света [27], явный вид соответствующего оператора можно найти в работе [28]. Для слабонаправляющих циркулярных волокон с параметрами Л~10-2-10-3 и kr0>>1 данное слагаемое имеет порядок (Л / r02)Et, где Et - поперечная компонента E . Отсюда находим порядок величины отношения АОВ к спин-орбитальному k02С05sANr0 / Л > 1, где k0=й / c, c - скорость света, что позволяет рассматривать скалярное волновое уравнение:

* 2 + £ ( r , ф , z , t ) a ² c ²       5 1 ²

—*

E =0.

В силу нестационарного характера проницаемости модели (4) решение (29) ищем в виде анзаца [29]:

E = J e m ( ^r , Ф )ехр( i ( P + mK ) z - ( ® + m ^ ) t ),    (10)

m=-да где в - искомая постоянная распространения. Полученную после подстановки бесконечную систему уравнений на Фурье-амплитуды удобно представить в виде уравнения на собственные функции и собственные значения:

H f + V af + V aoi ) | ф> = в ² | ф> .                 (11)

Здесь введено обозначение

1 V> = JmLem 1 m> с m =(…0, 1, 0,…)T, где <<1>> расположена на m-й позиции, T соответствует операции транспонирования. Первый оператор HIF управляет распространением света в невозмущенном изотропном циркулярном волокне и имеет вид:

H if = J [* 2 + ^е co k m — ² m^K в — m 2 K 2 ] I m X m \. (12) m = -да

Второй оператор V ^ˆ _AF описывает влияние линейной анизотропии:

Поскольку моды и спектр постоянных распространения анизотропного циркулярного волокна известны [28], в качестве оператора нулевого приближения удобно выбрать оператор H ₀ = T H_lF + V_4F .

2. Резонансная теория возмущений и резонансные моды

Собственные ф унк ц ₂ии уравнения нулевого приближения H ₀ \ ф> = в \ ф> являются линейно-поляризованными LP _t , n модами невозмущенного анизотропного циркулярного волокна [28] со всевозможными частотами ю _m = ю + m Q и k_m = ю _m / c , азимутальными I и радиальными n числами. Далее ограничимся рассмотрением случая взаимодействия фундаментальных I = 0 мод, в базисе линейных поляризаций ( E x , E y , E z ), представленных выражениями:

I                                                                                         I

\ m , LP, X >  = 1^ ( r ),0, KF l \ m > , l в dr J

I                                                                  I

\ m , LP 0y > = | 0, F 0 ( r ), . l \ m > , l ^{в dr} J

где мы опустили радиальное число, F 0 ( r ) – известное поперечное распределение поля [23]. Данным модам соответствуют зависящие от акустического волнового вектора K постоянные распространения:

xy вm = в0 + -~- - mK, вm = в0 - -- - mK,     (18)

2 ^в 0                      2 ^в 0

да

Т 7-           V^ 7 9 О . Г* I \ / I

Vaf = J km8sanS I mXm |, m=-да

в то время как АОВ описывается оператором V_AOI

вида:

где E = k ² 3s _AN , в 0 — известная скалярная постоянная распростра н ения [23]. Важно, что при резонансном значении K имеет место так называемое случайное вырождение спектра – пересечение определенных спектральных уровней [30]:

»          »»

Vaoi = Vaoi + Vaoi ,(14)

где да

m = -да

—ст —ст'

в m = в m ' ,

где ст = { x , у }. Из этого следует резонансное значение акустического волнового вектора:

Здесь n = C 0 3s an , ^ = (1 / 2) s co C o Krp 44 , а также

—ст —ст' в 0 -в 0 K =.

m - m '

B =

' 0

0 ,

0 ,

A

P =

( 0 0

_ч- sin ф

Поскольку

ˆ

HIF

ж k ² S co , V af

cos ф

- sin ф² cos ф . (16)

0 ?

« k ² 3s _AN , оператор

акустооптического взаимодействия может быть оце нен как VAOI ж C0k23sAN, легко видеть,   что

ˆˆ       ˆˆ

H IF / V AF ^{ж S} co / 3^s an ^ ¹ и V AF / V AOI ^Ж 1/ ^C 0 ^ ¹ , ^по-

скольку C 0 << 1 для всех экспериментально реализуемых параметров акустической волны, что соответствует иерархии операторов T H_IF ^ V_4F ^ V_4OI и позволяет рассматривать влияние АОВ как возмущение.

Данное кинематическое условие показывает, какие из базисных мод \ m , LP ₀ ^ст > и \ m ' , LPo ) могут быть эффективно связаны даже незначительным аку-стооптическим возмущением. Для рассматриваемого случая t = 0 мод существует три резонансные точки (рис. 1). Естественно, что для реального взаимодействия мод нулевого приближения построенный на них матричный элемент оператора АОВ должен быть отличен от нуля:

А        .      .

< m , LP o ^ст \ V AOI \ m ' , LP 7 > =                             (21)

= n[ k m - 1 3 m - 1, m ‘ + k m ₊ 1 3 m + 1, m ‘ ] ■ [З ст , x З ст' , у + З ст , у З ст' , x ] * 0.

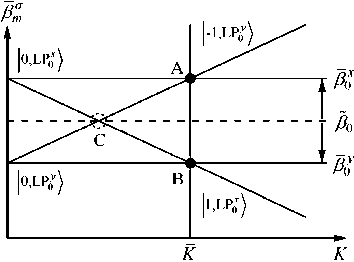
Рис. 1. Спектр постоянных распространения нулевого приближения в зависимости от акустического волнового вектора. Вертикальные стрелки показывают расщепления вырожденного по циркулярной поляризации уровня фундаментальной моды под действием линейной анизотропии. Указанные состояния удовлетворяют кинематическому и динамическому условиям резонанса и эффективно взаимодействуют в точках пересечения спектральных графиков <<А>> и <<В>>

Здесь использовано стандартное скалярное произведение с интегрированием по всему поперечному сечению волокна, 5 ij - дельта-символ Кронекера. Отметим, что вклад в матричные элементы (21) дает только оператор n B ^х C 0 5s AN , обусловленный гибридным действием оптического двулучепреломления 5s AN и акустической волны C 0 . В то же время фото-упругая часть оператора АОВ ^ P не обеспечивает связи мод нулевого приближения (17). Из (21) имеем следующие правила отбора для спариваемых мод нулевого приближения:

ст = { x , у }, ст' = { y , x}, m ' = m ± 1.              (22)

Первые два условия обусловлены тензорной природой оператора АОВ, в то время как последнее условие описывает эффект акустооптической перестройки частоты пучка. Легко видеть, что оптические моды вблизи резонансной точки > и <<В>> условиям (19) и (22) одновременно удовлетворяют наборы мод

• 10,    IP0 >,|-1, LP0y>,(23)

и

• 10,    IPy >,|1, LPox >

соответственно. Обе резонансные точки реализуются при резонансном значении

K = E « k ^ .(25)

P 0 V^s co

Отметим, что резонансное значение K определяется только величиной линейной анизотропии в отличие от случая изгибных акустических волн, где в условие резонанса вовлечены параметры А и r 0. Как хорошо известно [29], для определения структуры резонансных мод и спектра их постоянных распространения в окрестности точки случайного вырождения необходимо построить матрицу полного оператора Hij на тех базисных модах, которые одновременно удовлетворяют кинематическому и динамическому условиям резонанса.

Выполнив соответствующие вычисления, приходим к набору резонансных мод в окрестности точки >:

| y A >  = [ sin 0 1 IP ₀x > + cos 0 | IP ₀y > e^{i( n} t ^- Kz ) ] x x exp( i ( P A z -ю t )),

| v A >  = [ cos 0 1 IP ₀ x > — sin 0 1 IP ₀ y > e i ^{< n} t ^- Kz ) ] x x exp( i ( P A z -ю t )),

где cos_2 0 = s / ^s ² + Q ² , отстройка от резонанса s = K - K , интеграл перекрытия оптических состояний Q = k ₀ ² C ₀ 5s AN / P 0 . Модам (26) соответствуют спектры:

P A 2 = P 0 + E- + ¹ ( s±7i ^?T Q ² ) . ² P 0 ²

В окрестности резонансной точки <> имеем моды:

| y A >  = [ cos 0 | IP ₀ y > + sin 0 | IP ₀ x > e i ⁽ K ° t ) ] x x exp( i ( P B z -ю t )),

| y f >  = [ sin 0 | IP ₀ y > — cos 0 | IP ₀x > e i ⁽ Kz ° t ) ] x x exp( i ( P B z -ю t ))

и соответствующие им постоянные распространения:

&= ^e 0 - <+ 2 ( -s±vs 2 + q 2 ) .

Проанализируем полученные выражения для резонансных мод и их спектров. Вблизи резонансной точки <<А>> гибридные моды представлены взвешенной суперпозицией x -поляризованной LP 0 -моды на основной частоте ю - и у -поляризованной IP ₀-моды на сдвинутой вниз частоте ю - Q . Вблизи резонансной точки <<В>> моды являются взвешенной суперпозицией y -поляризованной LP 0 -моды на основной частоте ю - и x -поляризованной моды IP ₀ на сдвинутой вверх частоте ю + Q . Параметр 0 отражает конкуренцию между отклонением от резонанса s и силой межмодовой связи Q и управляет распределением энергии между парциальными ортогонально-поляризованными состояниями. Наибольшая степень гибридизации достигается при строгом выполнении резонанса ( s = 0). Видно, что постоянные распространения вблизи каждого резонанса невырождены по состоянию поляризации мод и демонстрируют наибольшее расщепление в резонансе при s = 0.

3.    Акустооптическая конверсия линейно-поляризованнных мод

Теперь можно перейти к изучению эволюции фундаментальной моды в волокне с бегущей крутильной механической волной. Рассмотрим возбуждение волновода x -поляризованной модой основного порядка на некоторой частоте ω :

| ψ in 〉 =|0, LP 0 ^x 〉 .                                      (30)

Очевидно, что такое поле возбудит в волокне суперпозицию мод резонансной точки <<А>> (26):

| ψ ( z ) 〉 = a 1 | ψ 1 ^A ( z ) 〉+ a 2 | ψ 2 ^A ( z ) 〉 .                  (31)

Условие сшивки поперечных компонент поля на входном торце волокна позволяет определить неизвестные коэффициенты a i и с точностью до общего фазового множителя записать поле в виде:

| ψ ( z ) 〉 = c 1 ( z )|0, LP 0 ^x 〉+ c 2 ( z )| - 1, LP 0 ^y 〉 , (32)

где весовые коэффициенты c 1,2 выглядят так:

c 1 ( z )=cos µ z + i cos2 θ sin µ z , c ₂ ( z ) = i sin2 θ sin µ z ,

где µ =(1/2) ε ² + Q ². Сохранение входящей энергии W 1 + W 2 = 1, где энергия парциального состояния W i = c i | ² сразу следует из (32). Из (32) и (33) следует, что при (i) строгом выполнении условия резонанса ε = 0 и (ii) оптимальной длине волокна z = L n :

L n

(2 n + 1) π

энергия падающей x -поляризованной LP 0 -моды оказывается полностью сосредоточенной в y -поляризованной моде на пониженной частоте:

| LP 0 x _〉 e - i ω t _→ | LP 0 y _〉 e - i ( ω-Ω ) t .

Проводя аналогичные вычисления для случая возбуждения в волокне y -поляризованной фундаментальной моды на основной частоте:

| ψ in 〉 =|0, LP 0 ^y 〉 ,

находим следующее выражение для распространяющегося в волокне поля:

| ψ ( z ) 〉 = c 1 ^*( z )|0, LP 0 ^y 〉+ c 2 ( z )|1, LP 0 ^x 〉 ,           (37)

с весовыми коэффициентами (33). Таким образом, в резонансе ε = 0 и на оптимальных длинах z = L n вся энергия оказывается аккумулирована в сгенерированной x -поляризованной моде на сдвинутой вверх частоте:

| LP 0 y _〉 e - i ω t _→ | LP 0 x _〉 e - i ( ω+Ω ) t .

Полученные строго в рамках развитой здесь теории АОВ трансформации мод (35) и (38) описывают экспериментально известные [22] преобразования ортогонально-поляризованных фундаментальных мод в резонансе.

Принципиально важным здесь является то, что полученные общие выражения (35) и (38) позволяют описывать преобразования возбужденных на входном торце волокна £ = 0 мод при произвольных оптических и акустических параметрах. В частности, они дают возможность изучить модовую трансформацию в спектральной области (рис. 2). Для построения спектральной характеристики предполагаем, что волокно имеет длину L ( P 0 , λ 0 ), оптимальную для полной трансформации мод при определенной акустичес ко й мощности P 0 , длине волны λ 0 и фиксированном K , при котором выполняется условие ε ( λ 0 )=0. С квантово-механической точки зрения, АОВ можно трактовать как фотон-фононное рассеяние, при котором сохраняются энергия, импульс и момент импульса взаимодействующих частиц. Согласно данной концепции, процесс преобразования мод (35) представляется как испускание фотоном с энергией Й ш и импульсом Й ( в ₀ + E / (2 в о )) фонона с энергией Й О и импульсом Й E / в ₀, что переводит его в состояние с уменьшенной энергией Й ( ш-О ) и импульсом Й ( в ₀ - E / (2 в ₀)). Обратно, процесс (38) предполагает поглощение таким же фотоном фонона с энергией Й О и импульсом Й E / в ₀, что переводит его в состояние с увеличенной энергией Й ( ш + О ) и импульсом Й E / в ₀. Отметим, что в данных процессах не реализуются процессы передачи спинового и орбитального угловых моментов между квазичастицами, поскольку они ими не обладают.

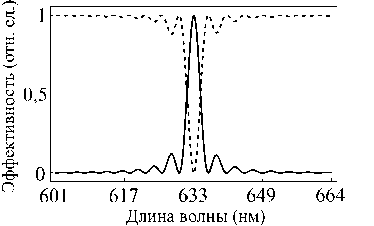
Рис. 2. Эффективность преобразований мод (35) и (38) в спектральной области. Пунктирная линия соответствует падающему на волокно полю, пунктирная – сгенерированному акустооптическим взаимодействием. Волокно имеет оптимальную для длины волны λ = 633 нм длину L = 26 см. Параметры волокна V = 2,96, r⁰ = 4,5 мкм, Δ = 0,001, δε AN = 2 ⋅ 10 –4 . Мощность акустической волны

P = 50 мВт, линейная частота f = 19,9 кГц

4.    Акустооптическая инверсия спинового угловогомомента t = 0 моды

Наконец рассмотрим эволюцию возбуждаемой на входном торце волокна циркулярно-поляризованной моды основного порядка на некоторой частоте ω . Такое поле является суперпозицией x - и y -поляризованных LP 0 с соответствующим сдвигом фазы:

| ^ n ) =|0, LP ox ) + i o |0, LP oy ) =| a) , (39) где a ±1 определяет направление циркулярной поляризации. Используя выражения (26) и (28) и пренебрегая несущественным общим фазовым множителем, находим:

| V ( z ^{) )} =

= [ C 1 ( z ) | 0, LP ox ) + c 2 ( z ) | - 1, LP oy )] e ^z +           (40)

+ i a[ c * ( z ) 10, LP oy )+ c 2 ( z ) 11, Lp )] e '^z , где Y = El 2 p ₀ +s/ 2 . В резонансе s = 0 имеем:

| ^ ( z ) ) = cos

—

Q ( P ) z 2

| ^LP 0x ^{) e}xp⁽ i -E z ) + i ^a | ^LP 0y ^{) e}xp^{( —} i Л- z ) ² P 0                        ² P 0

^^^^^^B

•   Q ( p ) z a sin ------

| LPo ) exp( i     z — Q t ) — i a | LPo ) exp( — i ²- z — Q t ) .

1 2 p 0       J                 1 2 p 0       Л

Известное выражение для вычисления cпинового углового момента (СУМ) параксиальных пучков позволяет определить проекцию СУМ поля (41) на направление распространения. В резонансе s = 0 имеем:

S_z ( z ) = h a cos [ Q ( P ) z ] cos [ Ez /P ₀ ] .              (42)

Видно, что знак и величина СУМ пучка определяется совместным действием АОВ и линейной анизотропии. Поскольку Q = C ₀ ( P ) E / p ₀ ^ E / p ₀, влияние АОВ может быть интерпретировано как модуляция обусловленных линейной анизотропией осцилляций СУМ пучка (рис. 3 а ). При длине волокна z = L = 2 n E / P ₀ выражение (42) упрощается: S_z ( z ) = h a cos [ Q ( P ) L ] . В этом случае знак и величина СУМ определяется акустооптической связью мод Q ( P ), что предопределяет возможность динамического и непрерывного контроля СУМ падающего поля путем простого варьирования акустической мощности P (рис. 3 б ). В таком режиме поле (41) может быть записано через циркулярно-поляризованные моды |± a ) так:

| у ( L ) ) =cos ( Q ( P ) L /2 ) | a) + + i a sin ( Q ( P ) L /2 ) | —a) ,

где мы пренебрегли частотной зависимостью парциальных состояний в силу соотношения Q / ю << 1. Заметим, что при некоторой акустической мощности P 1 такой, что sin( Q ( P 1 ) L /2)=± 1, поле (43) сводится к ортогонально-поляризованному состоянию | ^ ( L ) ) = |- a ) . Такое преобразование мод свидетельствует об акустически управляемой инверсии СУМ в полном соответствии с выражением (42). В волокне с параметрами V = 2,96, r 0 =4,5 мкм, А = 0,001, 5s AN =5 - 10 ^{- 5} , L =24,3 см, данный эффект может быть экспериментально реализован при акустической мощности P 1 =56 мВт.

В заключение покажем, что волокно с крутильной акустической волной в таком режиме способно генерировать пучки с локальным перепутыванием их поляризационных и частотных степеней свободы. Действительно, падающее поле:

| Фи ) = ( | x )+ i a | У ) ) | m ) ,

являющееся прямым произведением определенных поляризационных | p ) и частотных | m ) состояний, преобразуется в состояние вида:

| Ф out ) =| У ) | m + 1 ) + i a | x ) | m — 1 ) * | p ) | m ) ,       (45)

которое уже не может быть представлено в таком виде. Такое состояние соответствует так называемому максимально запутанному состоянию [30].

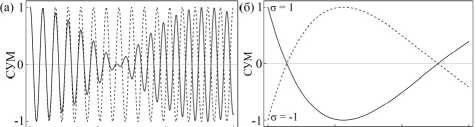
О 0,1          0,2          0,3 о so 100         150

z (м)                          Акустическая мощность (мВт)

Рис. 3. (а) График зависимости СУМ поля (39) от длины волокна при фиксированной акустической мощности P = 50 мВт. Сплошная линия соответствует эволюции поля при совместном действии АОВ и линейной материальной анизотропии, пунктирная – без АОВ. (б) График зависимости СУМ поля (39) от акустической мощности при фиксированной длине волокна z = 25,2 см.

Параметры волокна V = 2,96, r 0 = 4,5 мкм, А = 0,001, Sean = 5 - 10 5 . Частота акустической волны f = 198,5 кГц

Заключение

В данной работе мы исследовали эволюцию циркулярно-поляризованной фундаментальной моды в одномодовом анизотропном циркулярном оптическом волокне с бегущей крутильной акустической волной основного порядка. Структуры резонансных мод и спектра постоянных распространения получены путем применения резонансной теории возмущений к волновому уравнению. Изучена акустооптическая конверсия поляризационных мод, и установлено, что данные трансформации обусловлены влиянием антисимметричной части тензора деформации. Теоретически продемонстрирован эффект акустически управляемой инверсии знака спинового углового момента пучка. Показана возможность генерации запутанных состояний, в которых запутанными являются направление поляризации и частота пучка.

Данная работа выполнена при поддержке Российского научного фонда (проект № 20-12-00291-П).