Инверсия продольной составляющей спинового углового момента в фокусе оптического вихря с круговой поляризацией

В ряде работ [1 –6] сообщалось о появлении орбитального углового момента в сильном фокусе обычного циркулярно-поляризованного Гауссова пучка, который затем передавался микрочастице, помещенной в фокусное пятно. Это явление связано с преобразованием спинового углового момента (СУМ) в орбитальный угловой момент (ОУМ) и называется спин-орбитальной конверсией. Будучи лишенным орбитального углового момента, исходный пучок имеет только осевую проекцию вектора СУМ. Между тем в сильном фокусе наблюдается поперечный поток энергии, приводящий к ненулевой продольной проекции ОУМ. Спин-орбитальная конверсия в остром фокусе уже изучалась в работах [1 –6], но не было аналитического описания СУМ и ОУМ в рамках формализма Ричардса–Вольфа [7]. Теория Ричардса– Вольфа (ТРВ) [7], которая описывает электромагнитное поле вблизи острого фокуса, была обобщена на случай плоской границы раздела вблизи фокуса в [8]. ТРВ была также обобщена для резкой фокусировки цилиндрических векторных пучков в [9]. В [10] были рассчитаны только продольные компоненты СУМ и ОУМ с использованием ТРВ в остром фокусе светового поля с топологическим зарядом и круговой поляризацией. В [11] с использованием ТРВ изучалось усиление спин-орбитального взаимодействия вблизи фокуса при наличии двух границ раздела, образующих слоистую среду. В [12] спиновый эффект Холла был рассмотрен для Гауссова пучка в остром фокусе при наличии стратифицированной среды, как в [11]. Однако вышеприведенные статьи [8– 12] не содержат аналитических выражений, полученных в рамках ТРВ для всех компонентов орбитального потока энергии и спинового потока, а анализ таких выражений позволяет определить обратный поток энергии в остром фокусе. В [13– 17] вектор Пойнтинга (поток энергии) представлен в виде суммы орбитального потока энергии и потока спина. Поток спина не несет энергию, но является измеримой величиной [4, 18]. Наиболее эффективный подход к анализу световых полей вблизи острого фокуса дает ТРВ [7]. Она позволяет в замкнутом виде (то есть без использования рядов) описывать все компоненты электромагнитного поля вблизи фокуса для произвольного светового поля на входе в апланатическую оптическую систему. Чем больше фокусное расстояние по сравнению с длиной волны, тем точнее эта теория. В работах [8– 12] ТРВ позволила получить ряд физических величин в остром фокусе, таких как плотность потока энергии и плотность спинового потока, орбитальный угловой момент и спиновый угловой момент. Известны и другие приближенные [19] и точные [20–23] методы для описания электромагнитного поля вблизи резкого фокуса. Хотя эти методы точные, решения для компонентов электрического и магнитного полей выражаются либо через бесконечные ряды [20], либо через конечное число громоздких членов со специальными функциями [21, 22, 23]. Теоретический анализ точных решений уравнений Максвелла в фокусе затруднен. Кроме того, существует очень ограниченное число извест- ных точных решений уравнений Максвелла, в то время как ТРВ позволяет получать относительно простые замкнутые выражения вблизи острого фокуса для широкого класса начальных световых полей, таких как Гауссовы и Бесселево-гауссовы пучки, световые поля с целочисленным топологическим зарядом, световые поля с однородной (линейной, круговой, эллиптической) и неоднородной (азимутальной, радиальной) поляризацией. Поэтому мы используем эту теорию в данной работе. Имея только осевую проекцию СУМ, плоская волна с круговой поляризацией способна приводить во вращение поглощающую сферическую микрочастицу [24] и генерировать магнитное поле в немагнитных дисперсионных средах (эффект намагничивания) [25]. В [26] была продемонстрирована левитация сферических кварцевых частиц с низкими потерями в вакууме. Исследовано также вращение диэлектрических микрочастиц по круговому пути в сфокусированных лазерных пучках [11, 27]. В [12] наблюдалось вращение поглощающей асимметричной микрочастицы вокруг её центра масс, но частица располагалась в боковом лепестке дифракционной картины. Благодаря СУМ, световое поле может вращать любую поглощающую частицу и двулуче-преломляющую частицу, в том числе сферическую [24]. Вращение слабо поглощающей сферы вокруг своей оси в фокусе Гауссовского пучка с круговой поляризацией впервые было теоретически показано в [28]. Разложение вектора Пойнтинга на орбитальную и спиновую составляющие позволяет дать интерпретацию эффекту обратного потока энергии в сильном фокусе лазерного света [29, 30]. Например, в [31] обратный поток энергии (отрицательное значение осевой проекции вектора Пойнтинга) связывают исключительно с фазовой (вихревой) особенностью светового поля. Но это не совсем так, поскольку было показано, что обратный осевой поток энергии происходит в фокусе невихревого светового пучка [30]. Используя разложение вектора Пойнтинга на две составляющие, соответствующие орбитальному потоку энергии и потоку спина, мы предлагаем интерпретацию обратного потока энергии, который был известен в оптике довольно давно (с 1919 г. [32, 7]). Обратный поток энергии является довольно универсальным оптическим явлением, которое происходит не только в остром фокусе, но и в некоторых лазерных пучках, таких как, например, векторные X-волны [33], непараксиальные пучки Эйри [34] и дробные вихревые пучки Бесселя [35]. Обратный поток энергии имеет место в областях оптического поля, где осевая проекция спинового потока отрицательна и больше по величине, чем всегда положительная осевая проекция потока орбитальной энергии. Разложение вектора Пойнтинга на две составляющие [13– 17] приводит к тому, что угловой момент также разлагается на два слагаемых: СУМ и ОУМ [36]. В [37] (уравнение (4) в [37]) было показано, что, когда плоская волна с левой или правой круговой поляризацией дифрагирует на диэлектрической микросфере, азимутальная проекция СУМ и продольная компонента вектора Пойнтинга в рассеянном свете не зависят от спиральности. Однако поведение орбитального потока энергии и спинового потока в этой работе не обсуждается, хотя именно их соотношение определяет наличие обратного потока энергии. Как было показано в [17] для затухающих волн, поперечные компоненты СУМ не зависят от круговой поляризации, в то время как продольная компонента СУМ и поперечная компонента спинового потока зависят от спиральности (уравнения (8), (9) в [17]). Однако сравнение продольных компонент орбитального потока энергии и спинового потока (уравнения (8), (9) в [17]) показывает, что в этом случае нет обратного потока энергии.

В этой работе мы рассмотрим еще одно интересное оптическое явление, которое ранее не было замечено. А именно инверсию продольной компоненты вектора СУМ в остром фокусе в присутствии обратного потока на оптической оси. Ранее было показано, что в остром фокусе оптического вихря с топологическим зарядом 2 и левой круговой поляризацией на оптической оси формируется обратный поток энергии [29, 30]. Мы найдем проекции вектора СУМ в фокусе с обратным потоком и покажем, что продольная проекция СУМ положительная, то есть поляризация света в фокусе правая круговая, хотя исходный пучок имеет левую круговую поляризацию.

Спиновой угловой момент в фокусе Гауссова пучка с круговой поляризацией

Рассмотрим для сравнения фокусировку обычного Гауссова пучка с круговой поляризацией. С помощью формализма Ричардса–Вольфа [7] можно найти проекции вектора напряженности электрического поля в остром фокусе апланатической системы. Например, для начального светового поля с круговой поляризацией

A ( ° ) ( 1 1 n A ( ° ) f- i °)

I I , h = I I , V2 I i °)       V2 I 1 J

где σ=1 – правая круговая поляризация, σ = -1 – левая круговая поляризация, E и Н – вектора напряженности электрического и магнитного поля, в плоскости фокуса проекции вектора напряженности электрического поля будут иметь вид [6] для правой круговой поляризации:

E xR    - 2 ( 1 0,0 ⁺ e ^ 1 22 ) ,

E yR ^{= —}j=( I 0,0 - e ² ' ^ф I 2,2 ) , ₂,,

E zR = - V2 e ' ^ I_ц

и для левой круговой поляризации:

E xL =-2 ( 1 0,0 + e ^{- 2 ф} 1 ₂,₂ ) ,

E yL = ^^( ^- I 0,0 ⁺ e 2 i ^Ф I 2,2 2 ,                 ,

EzL = - 72e-i» 11,1, где

I v , H

f ) f sin ^{v+ 1}( - )cos^{3 -v} ( - ) x ,

X J ^J₀        2         2

x cos1/2 (9) A (9) eitzcos zJц (x) d 9, где λ – длина волны света, f – фокусное расстояние апланатической системы, x=krsinθ, Jμ(x) – функция Бесселя первого рода и NA=sinθ0 – числовая апертура. Начальная функция амплитуды A(θ) (предположим, что это действительная функция) может быть константой (плоская волна) или в виде Гауссова пучка f-Y9

A ^{( 9 )} = ^exPI   . _2n

( sin² 9 0

.

Найдем проекции вектора СУМ:

S = 2 Im [ E * x E ] ,

где Im – мнимая часть числа, E *– комплексное сопряжение вектора напряженности поля. Для правой круговой поляризации подставим (2) в (6) и получим в плоскости фокуса ( z = 0) (интегралы (4) – действительные функции):

S xR = - ( 1 0,0 + 1 2,2 ) 1 1,1 Sin Ф ,

S yR = ( 1 0,0 + 1 2,2 ) 1 1,1 COS Ф ,

SzR = 2 (10,0 — 12,2 ), и для левой круговой поляризации

S xL = — ( 1 0,0 + 1 2,2 ) 1 2,2 Sin Ф ,

S yL = ( 1 0,0 + 1 2,2 ) 1 1,1 COS Ф ,                              (8)

S zL =- 2 ( 1 0,0 — 1 2,2 ) .

Из сравнения (7) и (8) видно, что при смене направления вращения круговой поляризации в фокусе и направление вращения, и величина поперечной составляющей СУМ не меняются. А вот продольная составляющая СУМ меняет только знак. Для нас сейчас важно именно то, что при фокусировке света с левой круговой поляризацией в фокусе свет не меняет направление вращения вектора поляризации. Для левой поляризации вектор вращается по часовой стрелке, и поэтому продольная проекция СУМ отрицательная (8). А для правой круговой поляризации вектор поляризации вращается против часовой стрелки, и поэтому продольная проекция СУМ положительная (9). Левая круговая поляризация на входе так и осталась левой круговой поляризацией вблизи фокуса, также и правая круговая поляризация на входе остаётся правой круговой поляризацией в области фокуса. Также из (7) и (8) следует, что на оптической оси (r = 0) продольные проекции СУМ максимальны по модулю. Если на оптическую ось в фокусе поместить сферическую частицу с небольшим поглощением, то СУМ будет вращать эту частицу вокруг оптической оси и вокруг своего центра масс [28]. Для света с левой круговой поляризацией (8) частица будет вращаться по часовой стрелке, а для света с правой круговой поляризацией (7) – против часовой стрелки.

Далее мы покажем, что в случае фокусировки оптического вихря с круговой поляризацией в фокусе продольная проекция СУМ меняет свой знак по отношению к начальному СУМ пучка.

Спиновой угловой момент в фокусе оптического вихря с топологическим зарядом 2 и круговой поляризацией

Если на вход апланатической системы подать, вместо поля (1), поле вида

A ( 9 ) e m ^ф f 1

E =--—I

7 2 I i ст

A ( 9 ) e^{im ф} f- i o) H = ,

72   I 1 J

где m – целое число, топологический заряд оптического вихря, то с помощью формализма Ричардса– Вольфа в плоскости острого фокуса можно получить проекции вектора напряженности электрического поля для правой круговой поляризации

E xR = 72 ^ e^{4i ф} 1 2,4 + e^{2i ф} 1 0,2 ) ’

E yR = 2= ( e^{4i ф} 1 2,4 - e^{2i ф} 1 0,2 ) ,                        (10)

Ezr = 72e3iф 11,3, и для левой круговой поляризации

E xl = ^2 ( 1 2,0 + e^{2i ф} 1 0,2 ) ,

E yL =“/=( ^{- 1} 2,0 ⁺ e ² i ^Ф I 0,2 ) , 2 ,                ,

E_Z L =- 72 e i» 1 1,1 .

Мы выбрали топологический заряд оптического вихря m =2, так как только при этом значении топологического заряда вблизи фокуса на оптической оси у вихревого пучка будет иметь место обратный поток энергии для левой круговой поляризации [28]. Действительно, проекции вектора Пойнтинга (потока энергии) P =Re [ E *× H ]/2 имеют следующий вид в фокусе оптического вихря ( m =2) с правой круговой поляризацией

P xR = - 1 1,3 ( 1 0,2 + 1 2,4 ) Sin Ф ,

P yR = 1 1,3 ( 1 0,2 + 1 2,4 ) COS Ф ,                          (12)

PzR = 2 (102,2 — 122,4 ), и для оптического вихря (m =2) с левой круговой поляризацией

P xL = — 1 1,1 ( 1 0,2 + 1 2,0 ) Sin Ф ,

P yL = 1 1,1 ( 1 0,2 + 1 2,0 ) COS Ф ,                             (13)

P zL = 2 ( 1 02,2 — 1 2,0 ) .

Из (12) следует, что в фокусе поперечный поток энергии для оптического вихря с правой круговой поляризацией вращается против часовой стрелки, а продольная проекция вектора Пойнтинга на оптической оси равна нулю и вблизи оси положительна. Для оптического вихря с левой круговой поляризацией в фокусе из (13) следует, что поперечный поток энергии также вращается против часовой стрелки (как и для правой круговой поляризации), а на оптической оси продольная проекция вектора Пойнтинга максимальна по модулю и отрицательна ( P_zL ( z = r = 0) = - 1 ₂ ² ,₀ / 2). Если в плоскости фокуса расположить диэлектрическую частицу (с поглощением или без), то она будет вращаться по окружности против часовой стрелки. И направление её вращения не изменится, если изменить направление вращения поляризации в падающем пучке [38].

Далее рассчитаем проекции СУМ для случая фокусировки оптических вихрей с топологическим зарядом m = 2 и правой круговой поляризацией:

S xR = — 1 1,3 ( 1 0,2 + 1 2,4 ) Sin Ф ,

S yR = 1 1,3 ( 1 0,2 + 1 2,4 ) COS Ф ,

SzR = 2 (I02,2   I22,4 ), и левой круговой поляризации:

S xL = 1 1,1 ( 1 2,0 + 1 0,2 ) Sin Ф ,

S yL = — 1 1,1 ( 1 2,0 + 1 0,2 ) COS Ф ,                           (15)

S zL = 2 ( I 22,0 - I 02,2 ^{) .}

Из (14) следует, что для правой круговой поляризации поперечная составляющая вектора СУМ вращается вокруг оптической оси против часовой стрелки, а продольная проекция СУМ в фокусе на оптической оси равна нулю и вблизи оптической оси положительная. А для левой круговой поляризации из (15) следует, что поперечная составляющая СУМ вращается по часовой стрелке, а продольная проекция СУМ в фокусе на оптической оси положительная ( S zL ( z = r = 0) = 1 22,0 /2).

Таким образом, имеет место оптический эффект инверсии продольной составляющей СУМ, который не был замечен ранее. Суть эффекта в том, что исходное световое поле (9) с левой круговой поляризацией имело продольную проекцию СУМ на оптической оси отрицательную, а в фокусе вблизи оптической оси произошла инверсия и продольная проекция СУМ на оптической оси положительная. То есть если исходный вектор поляризации светового поля (9) с левой круговой поляризацией вращался по часовой стрелке, то в фокусе вблизи оптической оси вектор поляризации вращается против часовой стрелки, как в случае правой круговой поляризации. Этот эффект инверсии спинового углового момента в фокусе происходит в присутствии обратного потока энергии и может служить для его обнаружения. Действительно, из сравнения продольных проекций вектора Пойн-тинга (13) и вектора СУМ (15) видно, что они равны, но противоположны по знаку:

P zL =— S zL =— 2 ( 1 22,0 — 1 02,2 ) . (16)

То есть вблизи оптической оси в области фокуса именно в том месте, где имеется обратный поток энергии, происходит инверсия СУМ. Сферическая частица с поглощением, помещенная в фокус с центром на оптической оси в область обратного потока, должна вращаться вокруг оптической оси под действием спинового орбитального момента против часовой стрелки, хотя свет, освещающий эту частицу, имеет левую круговую поляризацию.

Моделирование

Для проверки теоретических предсказаний было проведено строгое численное моделирование. Моделирование проводилось с помощью разностного решения уравнений Максвелла FDTD – методом, реализованным в пакете RSoft FullWAVE, при следующих параметрах: длина волны λ = 0,633 мкм, апертура падающей волны D = 8 мкм. Падающее поле представляло собой плоскую волну единичной амплитудой с правой и левой круговой поляризациями и фазовым вихрем, умноженную на сферическую волну, сходящуюся на расстоянии f = 1,31 мкм (числовая апертура NA=0,95):

E x = exp ( i ( kf - m ф-ю t ) ) ,

Ey = exp(i I kf - mф - юt - в случае левой круговой поляризации,

E x = exp ( i ( kf - m ф-ю t ) ) ,

I                      n

E y = exp( i I kf - m ф - ю t + —

в случае правой круговой поляризации. Здесь m = 2 топологический заряд оптического вихря, k =2π / λ,

, _                        X, мкм J L

а)

£, отн. ед.

в)

ω – циклическая частота. Использовалась правая тройка векторов.

г)

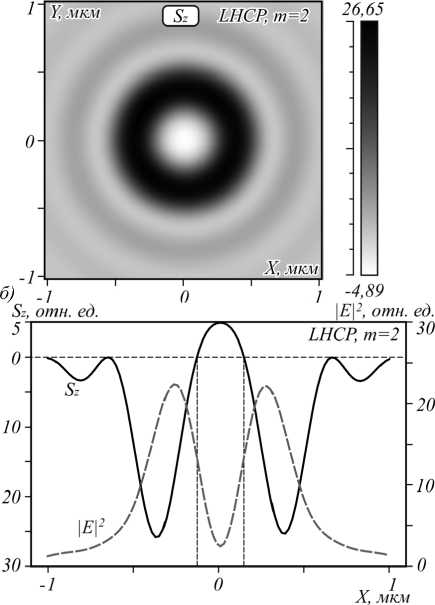
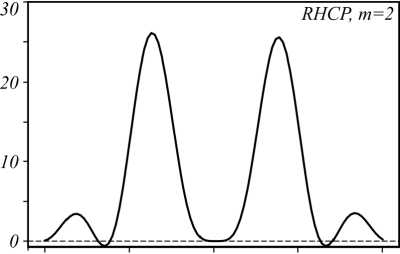
Рис. 1. Проекция на оптическую ось СУМ для падающего поля с правой (а) и левой (б) круговой поляризациями и с фазовым

вихрем порядка m = 2, а также их сечения соответственно (в, г) вдоль оси X. На график (г) наложена интенсивность | Е | ²

пучка

На рис. 1 показаны распределения в фокусе продольных проекций вектора СУМ и их радиальных сечений для начального оптического вихря с правой (а, в) и левой (б, г) круговой поляризацией. Из рис. 1 видно, что при падающем поле с левой круговой поляризацией и фазовым вихрем m =2 в центре образуется область с положительным значением вектора СУМ диаметром примерно 0,3 мкм. Положительная осевая проекция СУМ означает, что в этой малой области вблизи оптической оси в фокусе имеет место правая круговая поляризация. А это значит, что если туда поместить сферическую частицу с небольшой мнимой частью показателя преломления (с поглощением), то она будет вращаться вокруг оптической оси относительно своего центра против часовой стрелки. Хотя начальное световое поле имеет левую круговую поляризацию. Из рис. 1 б , г видно, что при r >0,3 мкм продольная проекция СУМ отрицательная, то есть вектор поляризации вращается по часовой стрелке, как у световой волны с левой круговой поляризацией. Если в эту область ( r >0,3 мкм) плоскости фокуса поместить ту же частицу, то она будет вращаться по часовой стрелке.

На рис.1 в видно, что на некоторых радиусах продольная проекция СУМ меняет знак. То есть на этих радиусах также происходит инверсия поляризации. Именно на этих радиусах возникает обратный поток

энергии (в данном случае тороидальный поток энергии). Действительно, из (12) и (14) следует, что P zR = S zR = ( 1 1,2 - 1 2,4 ) /2. То есть продольная проекция вектора Пойнтинга и вектора СУМ меняют знак на одних и тех же радиусах в фокальной плоскости, когда I 0,2 = I 2,4 .

Далее был проведен расчет момента силы, действующей на шар диаметром 250 нм, центр которого расположен в плоскости фокуса. Сначала решалась задача дифракции света с начальной амплитудой (18) на диэлектрическом шаре и рассчитывались все проекции электромагнитного поля вблизи шара. Расчет светового поля осуществлялся методом FDTD. Момент силы рассчитывался с помощью тензора напряжений Максвелла:

M = cf[ r x ( ^ - n ) ] d S , (19)

S

где n – нормаль к поверхности S , охватывающей частицу (шар), r – радиус-вектор из точки в центре шара, относительно которой рассчитывается момент, к поверхности S, ст - тензор напряжений Максвелла, компоненты которого в системе СГС имеют вид:

^CT ik = "^—

4 n

1 fl El²+1 HI

5 ,

)

- E i E k - H i H k

где E i , H i – компоненты электрического и магнитного полей, δ ik – символ Кронекера.

Мощность падающего пучка была принята 100 мВт. Сетка отсчетов в FDTD-методе была λ / 80 в области, где расположена частица (в границах – 1,5< X <1,5; -0,65< Y <0,65, 0,3< Z <2), во всей остальной области она была равна λ/30. Момент сил для шара с показателем преломления n = 1,5+0,01 i и с центром в плоскости фокуса на оптической оси получился равным M z = 3,23 ⋅ 10^-21 Нм. Для частицы с большим поглощением n = 1,5+0,3 i момент сил увеличился и стал равным M z = 7,9 ⋅ 10^-20 Нм. На рис. 2 приведен график зависимости продольной проекции момента силы M z от смещения центра шара в плоскости фокуса вдоль оси X в диапазоне от 0 до 1 мкм с шагом 50 нм. Из рис. 2 видно, что момент M z вблизи оптической оси положительный и вращает шар против часовой стрелки.

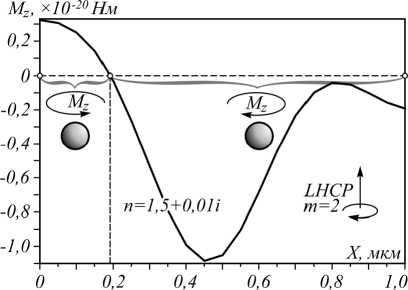
Рис. 2. Зависимость момента M z от смещения шара в плоскости фокуса вдоль оси X

Это аномальное вращение происходит в области обратного потока энергии. При смещении центра шара с оптической оси в плоскости фокуса момент меняет знак при X = 0,19 мкм и становится отрицательным. В этой области, где продольная проекция момента сил отрицательна, шар вращается нормальным образом по часовой стрелке, то есть так же, как вращается вектор поляризации света с левой круговой поляризацией.

Заключение

С помощью теории Ричардса–Вольфа получены аналитические выражения для проекций спинового углового момента и вектора Пойнтинга в фокусе Гауссова пучка с круговой (левой и правой) поляризацией, а также для оптического вихря с топологическим зарядом 2 и круговой (левой и правой) поляризацией. Показано, что СУМ для Гауссова пучка с левой круговой поляризацией имеет в фокусе на оптической оси отрицательную продольную компоненту СУМ, а для правой круговой поляризации – положительную. И наоборот, при фокусировке оптического вихря ( m =2) с левой круговой поляризацией в фокусе на оптической оси продольная компонента СУМ положительная, а для правой круговой поляризации – отрицательная.

Такое аномальное поведение продольной компоненты СУМ объясняется тем, что при фокусировке оптического вихря ( m =2) с левой круговой поляризацией в фокусе на оптической оси формируется обратный поток энергии (отрицательная проекция вектора Пойн-тинга). Показано также, что при фокусировке оптического вихря ( m =2) c правой круговой поляризацией на некоторых радиусах в плоскости фокуса, где возникает тороидальный поток энергии, также происходит инверсия СУМ (продольная компонента СУМ меняет знак). На этих радиусах у поля имеет место левая круговая поляризация, хотя фокусировалось световое поле с правой круговой поляризацией. Численно с помощью строгого расчета поля в области фокуса с помощью FDTD-метода показано, что продольная компонента СУМ ведет себя в плоскости фокуса, как предсказывает теория. Также строго (без дипольного приближения) с помощью тензора напряженности Максвелла рассчитан момент сил, действующий на наношар с комплексным показателем преломления, центр которого помещен в плоскость фокуса. На шар действует момент сил, осевая проекция которого положительна вблизи оптической оси. То есть шар будет вращаться против часовой стрелки, хотя освещающее световое поле имеет левую круговую поляризацию и вектор поляризации вращается по часовой стрелке. Найденное аномальное поведение вектора СУМ в фокусе в области, где имеет место обратный поток энергии, служит физическим доказательством существования обратного потока энергии в фокусе и средством его обнаружения.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант 18-2920003 в части «Спиновой угловой момент в фокусе оптического вихря с топологическим зарядом 2 и круговой поляризацией»), Российского научного фонда (грант 18-19-00595) в частях «Спиновой угловой момент в фокусе Гауссова пучка с круговой поляризацией» и «Моделирование», а также Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН в частях «Введение» и «Заключение».