Инвестиционные технологии в управлении развитием инфраструктуры городских систем

Проблемы целенаправленного влияния на развитие города являются одними из главных, от решения которых во многом зависят условия жизни миллионов людей и рост эффективности общественного производства. Особое значение они приобретают в условиях развивающейся экономики , когда необходимо оперативно реагировать на факторы нестабильности отдельных секторов и форм концентрации производства, сохраняя при этом стратегические тенденции в развитии города. Собственно, гра-достроительств о, связано, в первую очередь, с инвестиционным аспектом этих процессов, т.е., с проблемой развития.

Сеть городов образует территориальноэкономический базис “опорный каркас” геоин-формационной решетки системы расселения России. Задавая внутреннюю структуру поселения, региональная система стимулирует необходимость в динамике увязать региональное развитие с городским – “управление через урбанизацию”. При этом инфраструктурные проекты (далее по тексту «проект») являются катализатором комплексного прогнозирования социокультурной среды.

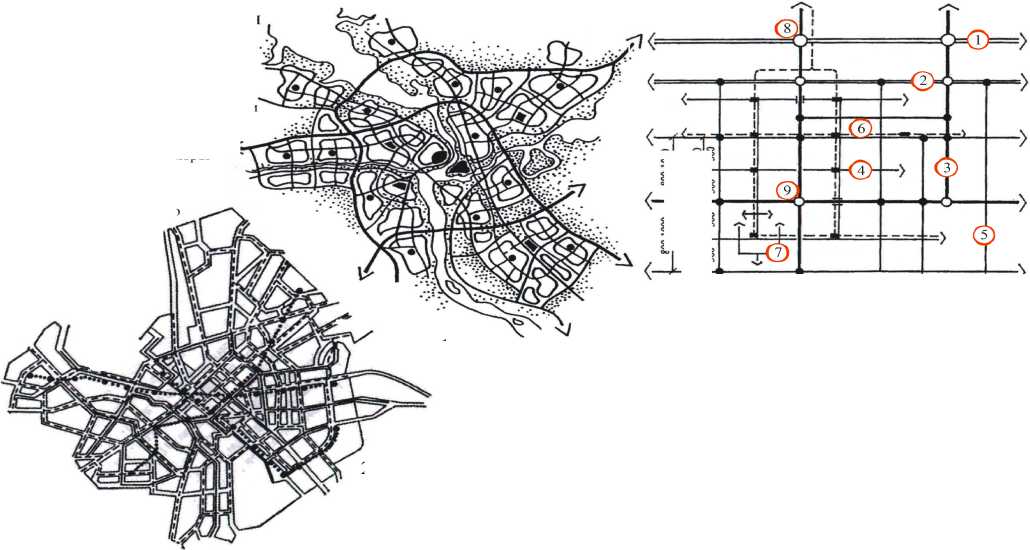
Для многих исследователей наиболее важным аспектом этой проблемы является то, что именно инфраструктура образует техникоэкономическое ядро городских систем. Это нашло отражение в известном и, пожалуй, наиболее фундаментальном для градостроительства понятии “каркас” (рис. 1), которое в данном случае должно рассматриваться не с морфологической, а с экономической стороны

Город выступает как активный субъект хозяйственной жизни. Это требует внесения в экономическую политику серьезных изменений. Их суть – учет интересов города и создание условий, необходимых для выполнения его администрации задач обустройства территории и развития человеческих ресурсов. И вот здесь на первый план выходит частный бизнес. Потенциальные инвесторы требуют достаточно четких обоснований своих инвестиций. В этом случае инвестиционный потенциал конкретных районов развития рассматривается и анализируется на основе многокритериальной оценки. А это, безусловно, предмет и задача управления.

В аспекте качественного совершенствования города инвестиционный проект должен исходить из необходимости целенаправленного усложнения и обогащения его структурнофункциональной организации. При этом увеличивается диапазон и свобода выбора различных типов поведения и соответствующих им форм организации пространства, что является однозначным функционалом управления (табл. 1).

Линия рельсового транспорта

1 - Структуроформирующая роль автомобильных дорог и магистральных улиц

Внешние скоростные дороги Городские магистрали Прочие улицы и дороги Общественные центры

Л иния наземного безрельсового транспорта

§

i

I

I

I

I

250-300 м

■800-1000-

1-внешняя скоростная дорога; 2-городская дорога (кольцевая с хордами, и рад иусами, образующими равнозначные сегменты) ; 3-общегородская магистраль с непрерывным движением; 4-общегородская магистра ль с регулируемым движением; 5-магисталь районного  значения;

6-трасса скоростного рельсового трансп орта; 7-местный про езд ; 8-транпортный узел высшего класса; 9-прочие пересечения

2 - Организация пассажирского Принципиальная схема трассировки - 3 транспорта (по Малояну Г.А.)          магистральных улиц и дорог

(интерпретация авторов)

800-1000

■ 500-4=- 500-^———4-1400-1600Ж

§

Рисунок 1. Транспортная инфраструктура как элемент инвестиционного потенциала

Таблица 1 . Функции управления

Процессное управление (функции и задачи)	планирование	организация	стимулир ование	контроль
Проектное управление (фазы проекта)	концепция	разработка	реализация	завершение
Управление деятельностью (процессуальные компоненты)	цель	способ	мотив	результат

В процессном управлении выделяют следующие основные функции: планирование, организация, мотивация (стимулирование) и контроль. В данном случае процессное управление является предметом научного исследования. Важно подчеркнуть, что одна и та же сторона предмета научного исследования, может рассматриваться как задача или проблема на стыке изысканий различных наук.

В проектном управлении в соответствии с фазами жизненного цикла проекта выделяются:

• •    начальная фаза (концепция): сбор исходных данных и анализ существующего состояния; определение целей задач, критериев,

требований и ограничений (внешних и внутренних) проекта, экспертиза основных положений, утверждение концепции проекта;

• •    фаза разработки: формирование команды, развитие концепции и основного содержания проекта, структурное планирование, организация и проведение торгов, заключение договор ов и субдоговоров с основными исполнителями, представление проектной разработки и ее получение одобрения;

• •    фаза реализации проекта: ввод в действие разработанной на предыдущих фазах системы, организация выполнения работ, ввод в действие системы мотивации и стимулирования исполнителей, оперативное планирование,

управление материально-техническим обеспечением, оперативное управление;

• •    завершающая фаза: планирование процесса завершения проекта, проверка и испытание результатов реализации проекта, подготовка персонала для эксплуатации результатов реализации проекта, их сдача заказчику, реализация оставшихся ресурсов, оценка результатов и подведение итогов, расформирование команды проекта.

В этом случае проектное управление выступает в качестве конкретного инструмента деятельности - метода исследования. В соответствии с логикой научного поиска осуществляется разработка комплекса теоретических и эмпирических способов исследования, сочета ние которых дает возможность с наибольшей достоверностью познать сложные и многофункциональные объекты.

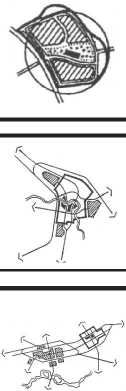
Обычно при рассмотрении механизмов управления проектами, особенно если это касается проектов территориального размещения, практически не рассматривается динамика реализации проекта во времени [1, 2, 3]. Это обусловлено статичностью компонентов городской инфраструктуры. Их динамические состояния (рис. 2), применительно к планировочным и транспортным каркасам городов, практически не рассматриваются с точки зрения полезности использования их геоинформационного размещения и управления объектами перемещения.

Потенциал планировочной

V структура города /

Вектор развития сегменто

• V инфраструктуры /

  Стабильные территории

  
  
  
  
  

  Равновесные территории

  
  

  Динамичные территории

  
  
  
  
  

  Общественные центры Сфера культурнобытовых услуг

  Улично-дорожная сеть

  Торговые предприятия, в зависимости от степени

  насыщения торговыми функциями, структуроформирующие дороги

  Жилые территории

  Крупные торговые комплексы

  Школы, детские сады

  Спортивные сооружения

  

  Прозрачные режимы ранжирования типов городской системы, прогнозирование регламентов застройки

  Стимулирование отдельных составляющих равновесия в циклы приращения

  Пофакторная оценка динамики развития, которая показывает по стоянный хар актер с большим пер иодом изменений

  
  

  Рисунок 2. Структурная интерпретация развития территорий по динамическим показателям

  
  

Действительно, при решении задачи синтеза того или иного механизма неявно предполагается, что механизм «включается» в момент начала выполнения проекта и однозначно определяет результаты деятельности всех исполнителей и результат всего проекта в целом. Такое одношаговое описание проекта адекватно многим реальным ситуациям, однако, далеко не всем из них [4, 5].

Если перед началом проекта и центр, и исполнители имеют достаточно полное и точное представление обо всех параметрах самого проекта и параметрах внешней среды, существенно влияющих на результат реализации проекта, то все возможные ситуации могут быть учтены (например, в рамках метода сценариев) при синтезе механизма управления на начальном этапе [2]. Такой механизм может оказаться достаточно громоздким, так как он должен учитывать значительное число факторов.

На практике ситуации, в которых априори имеется полная информация о будущих значениях существенных параметров, встречаются достаточно редко. Зачастую имеется большая неопределенность относительно результатов реализации проекта. Понятно, что со временем эта неопределенность будет умень- шаться за счет поступления новой информации, идентификации параметров, наблюдений за ходом реализации проекта и т.д. В этом случае создавать механизм управления (рис. 3), который изначально учитывал бы всю неопределенность и давал универсальные рецепты (идеальные модели) на все случаи жизни, неэффективно, а порой просто нереально [2].

Исходя из вышеизложенного, возникает необходимость реализовывать проект в динамических вероятностных характеристиках. Наиболее простым обобщением статических моделей на динамический случай является следующее рассуждение. Пусть процесс реализации территориального размещения объектов различных функций разбит на T периодов. В каждом отдельно взятом периоде центру необходимо решать задачи распределения ресурса, синтезировать механизмы финансирования, стимулирования и т.д. Если считать, что ставить и решать эти задачи для статических моделей (одного периода) представляется возможным, то необходимо просто решить N задач

• - каждую для своего периода. Такая модель называется квазидинамической (или моделью с несвязанными периодами функционирования) [5]. Квазидинамические модели позволяют описывать динамику процесса, но при их использовании некоторые эффекты, связанные именно с динамикой, могут быть потеряны. Поэтому иногда более адекватными являются динамические модели, в которых задачи, решаемые в каждом периоде, связаны между собой.

Следует признать, что, во-первых, динамические модели являются несравненно более сложными (с точки зрения проблем синтеза, вычислительной сложности, анализа решений и т.д.), чем статические. Во-вторых, модели, достаточно полно учитывающие динамику, исследованы гораздо менее глубоко, чем статические модели. Результаты исследования некоторых динамических активных систем приведены в работах [1, 5, 6] и эти результаты можно использовать при решении задач оптимального управления.

Система

Теоретическое исследование

Описание системы и

построение модели

Задача синтеза управлений

Анализ модели i

Исследование устойчивости решений ।

Имитационное моделирование

Идентификация

Настройка модели

Рисунок 3. Технологическая процедура принятия решения в задачах управления

Принцип Беллмана дает достаточные условия оптимальности процесса в задаче оптимального управления[7, 8]. Он базируется на следующем ключевом факте:

Если кривая х*(t) является оптимальной траекторией в задаче управления динамической системой на отрезке времени [t0, T], с некоторым начальным условием х(t0) = х0, то для любого момента времени т е[t0, T] оптимальным решением задачи управления системой на от резке времени [т, T] с начальным условием х(т) = х*(т) будет являться участок той же самой траектории х*(t). Рассмотрим задачу оптимального управления в виде:

t 1

J(х(•), u(t)) = jF(t,х (t), u(t))dt + t 0

. .+ Ф ₀( 1 1 , х ( 1 1 )) ^ max.                (1)

х ( t ) = f ( t , х ( t ), u ( t )), х ( t о ) = х о ,        (2)

u ( t ) E U t ,                               (3)

и пусть J * - значение функционала на оптимальном ее решении ( x *( t ), u *( t )).

Теперь для произвольного момента времени т e [ t о , T] и произвольной точки фазового пространства у положим в задаче (1 -3) 1 ₀= т , x ( т )= у . Функцию J *( т , у ), равную значению функционала на оптимальном решении такой задачи, будем называть функцией Беллмана или функцией выигрыша.

Отметим, что J * = J *( 1 ₀, x ₀).

Исследуем теперь изменение функции J *( t , x ) с течением времени вдоль оптимальной траектории системы, то есть, при x = x *( t ).

Рассмотрим малое приращение времени dt . За это время система перейдет в новое состояние

x*(t + dt) ~ x*(t) + dx*(t), где, из (2), dx*(t) = f(t, x*(t), u *(t))dt.

Изменение значения функционала (1) на отрезке [t, t + dt] может происходить только за счет интегральной его части и приближенно составляет j* F(t, x *(t), u *(t)) dt ~ F(t, x*(t), t u *(t))dt, а оставшаяся часть, согласно принципу оптимальности Беллмана, будет равна J*(t+dt,x*(t+dt)). Таким образом, получено следующее рекуррентное соотношение [8]:

J *( t , x *( t )) » F ( t , x *( t ), u *( t )) dt + J *( t

+ dt , x *( t + dt )).                         (4)

Теперь, пользуясь оптимальностью u *( t ), можем переписать (4) следующим образом:

J *( t , x ( t )) ~ max { F ( t , x ( t ), u ( t )) dt + u ( t ) e U,

J *( t + dt , x ( t + dt ))}.                (5)

Далее, в предположении дифференцируемости J *( t , x ) по своим аргументам, переходя к пределу при dt ^ 0 получим следующее соотношение:

d J * ( t , x )

---—- = max { F ( t , x ( t ), u ( t )) + d t         “ ( t ) e U ,

5 J * ( t , x )

—-—- ftt , x ⁽ t ), u ⁽ t ^))}.         ⁽⁶⁾

∂ x

Соотношение (6) представляет собой дифференциальное уравнение в частных производных первого порядка для определения функции J *( t , x ). Оно называется уравнением Беллмана в дифференциальной форме.

Краевым условием для данного уравнения является оптимальное значение функционала при t = 1 1 , равное терминальному члену:

J *( 1 1 , x ( 1 1 )) = Ф о ( 1 1 , x ( 1 1 )).               (7)

Как правило, аналитическое решение уравнения (6) найти довольно сложно или вовсе невозможно. Поэтому прибегаем к дискретизации задачи (1 - 3) с последующим ее численным решением. Дискретная задача формулируется следующим образом [8]:

N - 1

J ( x ( • ), u ( • )) = £ F ( t , , x„u i ) A t i + Ф o ( x n ) ^

i = 0

max.(8)

xi+1 = fx,, u,), xо - задано.(9)

ui E Ui,(10)

Отметим, что в дискретной задаче состояние системы будет описываться вектором x =( x ₀, x 1 ,..., x_N ) e R N ⁺¹, а управление - вектором u =( u 0 , u 1 ,., u n -1 ) e R .

Для (8) - (10) уравнение Беллмана будет иметь следующий вид:

J*(x ) = max { F ( t , x , , u , ) A t , + J +1 *( fx„ u , ))}, u _i ∈ U _i

(11) с краевым условием J_N *( x_N ) = Ф ₀( x_N ).

Решение задачи (11) при заданных краевых условиях производится последовательным решением уравнения (11) для шагов , = N -1, N -2, ., 0 (обратный ход метода Беллмана). При этом на каждом шаге получается оптимальное управление u , * как функция от текущего состояния системы x , . На втором этапе по полученным функциям u , *( x , ) производится синтез оптимального управления для задачи с конкретным начальным условием x ₀.

Таким образом, метод динамического программирования, в отличие от рассмотренных выше необходимых условий, дававших оптимальное управление как функцию времени u *( t ) (программное управление), позволяет определять оптимальное управление как функцию состояния системы u *( t , x ) (синтезированное управление), что дает возможность отыскивать решение сразу для целого класса задач с различными начальными условиями [7].

Далее будем считать, что в функционал задачи время не входит явно. Положим шаг A t , равным 1. Введем понятие горизонта планирования как количества шагов, оставшихся до завершения управления. Обозначим

Vk (x) = JN-k *(x), т.е. максимальный выигрыш, который можно получить за к* шагов, если начать из состояния x. В этом случае рекуррентное соотношение для Vk(x) принимает вид:

V_k ( x ) = max { f ( x, u ) + y^ ( fx, u )),    (12)

u∈ U с краевым условием: V0(x) = Ф0(x).

Для реализации проекта по территориальному размещению объектов различных функций имеется некоторый ресурс в объеме, D > 0, который необходимо распределить между N объектами, так, чтобы максимизировать их суммарную полезность, если функция полезности i -го объекта F i ( u i ) = ln u i , где: u i - объем ресурса, получаемый i -м объектом. (Считаем, что объекты перенумерованы согласно точек не-котрой градостроительной модели).

В формальной постановке задача имеет вид:

N

J ( u ) = S ln ^ui ^ max; (13)

i = 1

N

^ u_t <  D ; D > o.

i = 1

Приведем ее к задаче оптимального управления. Для этого необходимо выделить переменную, являющуюся аналогом времени (номера шага) в задаче оптимального управления, горизонта планирования, а также параметры состояния и управления в каждый момент времени.

Пусть номером шага в задаче является номер объекта i, для которого принимается решение о распределении ресурса. Тогда величина ui будет являться управлением на i-м шаге. Введем параметр состояния системы xi как объем ресурса, имеющийся к i-му шагу (i = 1, N). Тогда, из условия задачи получаем xi+1 = xi — ui; x 1 = D. (14)

Так как может быть распределено ресурса не более чем имеется в наличии, то имеет место ограничение на управление

0 <  u i <  x i. (15)

Таким образом, (13 - 15) представляет собой задачу оптимального управления в дискретном времени. Решим ее с использованием принципа Беллмана [8]. Обозначим через Vk(x) значение функции выигрыша, когда горизонт планирования равен к*, т.е. ресурс х распределяется между n агентами (не важно, что последними, так как все агенты имеют одинако- вые функции полезности, что очень существенно при формировании равномерного расширения границ города на всех направлениях).

Рассмотрим следующий шаг в задаче, который имеет место после того, как ресурс полностью распределен между всеми агентами. Согласно краевому условию функция Беллмана V ₀ на этом шаге равна V ₀( x ) = Ф ₀( x ) = 0.

Рассмотрим теперь ситуацию, когда ресурс должен быть распределен одному агенту. В этом случае горизонт планирования к = 1 и рекуррентное соотношение (12) принимает вид:

• V 1 ( x ) = max {ln u + V ₀( x - u )} = ^ 0 <  u <  x

. .= max {ln u } = ln x , откуда u_N *( x ) = x .

0 < u <  x

Аналогично, при горизонте планирования к^* = 2 имеем:

• V 2 ( x ) = max { ln u + V 1 ( x - u )} = .

0 < u <  x

. .= max {ln u + ln( x - u )}. 0 < u <  x

Максимум выражения в фигурных скобках по u е [0, x ] достигается при u* ( x )= —,

x при этом V2(x)=2ln —. Значит, оптимальное управление в этой ситуации uN-1 *(x) = x.

Покажем далее, что для горизонта к * = 0,., N оптимальное управление на шаге ( N +1- к * ) и функция Беллмана горизонта к * имеют вид:

u n +1 - к * ( x ) = x , V k ( x ) = к * ln x . (16) к * к *

Предположим, что это верно на некотором шаге ( N +1- к * ). Определим оптимальное управление и функцию Беллмана горизонта к * [8]:

Vk+1(x) = max {ln u + Vk(x - u)} = 0< u < x max {ln u + к* ln x-u}.

0 < u < x                       к *

Обозначим A ( u ) = ln u + к * ln —-—.

Условия первого порядкa мaксимумa функции

A ( u_{N - к} ) имеют вид:

dA ₌1_ к * = ₀

du u x- u откуда un-к *( x) = —x , Vk+1(x) = (к*+1) ln —x .

к + 1                      к + 1

Таким образом, определен общий вид оптимального управления для произвольного шага в задаче. Теперь проведем синтез оптимального управления для задачи с N объектами и начальным объемом ресурса, равным D:

xD и 1 *( x 1) = — = --;   x 2 = x 1 - u 1

NN

= D ( N - 1)

D

* = D--

N

N ’ xD и 2 *( x2) =--— =   ;   x3 = x2 - u 2

N - 1 N

* =

^{D (} N ^- 1) _- D = D ( N - 2).

NN N

U k * ( x k ) =-----—- =   ; x k +1 = x k - U k * =

N + 1 - k N

D ( N + 1 - k ) _ D = D ( N - k )

N N N ’

Таким образом, в данной задаче опти- мальным является равномерное распределение ресурса между всеми агентами:

и * = ( D , D , ..., D ).           (17)

NN N

Наиболее характерный недостаток со- временных градостроительных планировочных документов и правил заключается в том, что они не в полной мере учитывают естественную динамику городских процессов. Даже тогда, когда оказывается правильным исходный прогноз увеличения размеров границ поселений, в процессе эволюционного усложнения внутренней структуры объекта генеральный план нередко обнаруживает свою низкую социальную и транспортную эффективность. Неравномерное приращение городских районов относительно друг друга нарушает первоначальные планировочные и функциональные связи, не удается достичь органического единства старых и новых характеристик пространства. Целостность транспортной системы нарушается. Это выражается в закупорке транспортных артерий от непродуманных решений, которые образуют тромбы от точечной и уплотнитель- ной застройки, неэффективным регулированием скоростных режимов, бестолковым планированием развязок и путепроводов. Эффективность функционирования различных логистических подсистем, связующим звеном которых является транспорт, объективно низка.

Математическое утверждение равномерного распределения ресурса агентам конкретных градостроительных моделей, входящих в урбанизированный каркас городской инфраструктуры, подразумевает соответствующее равновесие ёмкости пунктов отправления-прибытия. В гносеологическом смысле это можно трактовать как пропорциональное поступательное приращения всей городской системы. Это исключает перекосы и концентрацию отдельных направлений территориального роста, являясь катализатором инвестиционной политики, различного уровня администрирования и бизнеса.