Investigations of Cellular Automata Game of Life Rules for Noise Filtering and Edge Detection

Published Online April 2012 in MECS

Ulam [1] and Von Neumann [2] at first proposed Cellular Automata (CA) with the intention of achieving models of biological self-reproduction. After a few years, Amoroso and Fredkin and Cooper [3] described a simple replicator established on parity or modulo-two rules. Later on, Stephen Wolfram formed the CA theory [4],[5]. Nowadays, CA are widely used in many tasks because of their useful characteristics and various functions. CA are models for systems which consist of simple components and behavior of each component is obtained and reformed upon the behavior of its neighbors and their previous behavior. The constructing components of these models can do robust and complicated tasks by interacting with each other. Cellular automata are widely used in many areas of image processing such as de-noising, enhancing, smoothing, restoring, and extracting features of images.

Detecting the edge components of the image, one of the most important image processing tasks, is used for object background separation, 3-D interpretation of a 2-D image, and pre-processing in image understanding and recognition algorithms [6],[7]. It usually gives as output a binary image in which the edge points have been highlighted. Edge detection is a mandatory step in many image analysis procedures, and the quality of edge detection is a crucial characteristic [8]. Quality is assessed in two different ways: accuracy of edge detection, and level of connectivity in continuous edges. If some edges are still unconnected after edge detection, then an additional edge linking process is required [9],[10].

In transmission process, the data value of input image will suffer from various kinds of noises. These sources of noise may come from external interferences, e.g. atmospheric noise, man-made noise, that will cause the perturbations to the system. These perturbations can produce the wrong information in system operation. The random disturbances in the images are shown as noise and are often caused by the malfunctioning pixels in camera sensors, faulty memory locations in hardware or transmission in the noisy channel. The noises well reduce the quality of images and damage the expression of information for images effectively. Suppose if the images are corrupted by noise it smears some details and thus resulting in inaccurate edge detection.

Image filtering can effectively reduce the noise and make the image smooth. The common methods of image filtering in general are spatial filtering and frequency domain filtering. The goal of impulse noise removal is to suppress the noise while preserving the integrity of edge and detail information, to reduce the degradation related to noise of any kind, a preprocessing or filtering step could be applied [16]. There has been a lot of effort in designing an efficient filtering algorithm. Median filter has been known to perform better in removing impulse noise than the linear filters [17][18]. Others are adaptive median filter [19] and progressive switching median [20]. In this paper, we present a filter based on cellular automata, which is used to remove impulse noise from noise-corrupted images [21][22],[26].

There are many methods for edge detection, and most of them use the computed gradient magnitude of the pixel value as the measure of edge strength [11]. The early days of works on edge detection are done by Sobel and Roberts [28]. Their detection methods are based on simple intensity gradient operators. Later on, much of the research works have been devoted to the development of detectors with good detection performance as well as good localization performances. A different edge detection method i.e. Prewitt, Laplacian, Roberts and Sobel uses different discrete approximations of the derivative function. For comparison purposes, we have used here four most frequently used edge detection methods namely Sobel edge detection [29], Prewitt edge detection [29], Canny edge detection [31] and Roberts edge detection[30].

A method for the evolutionary design of CA rules for edge detection was proposed by Batouche et al. [12], [15]. Two dimensional binary CA are used for binaryimage edge detection, and transition rule evolution is guided by a genetic algorithm. Another application of this method was done by Rosin and the method was extended to handle gray-scale images [13]. The images are decomposed into a number of binary images with all possible thresholds. Each of the binary images is processed using binary CA rules. Rosin later applied an improved version of this method to edge detection [14]. However, this method has a very long calculation time due to the iterative process used for hundreds of binary images.

In this paper a new and optimal approach of noise filtering and edge detection based on Cellular Automata Game of Life (CA GoL) has been proposed. The idea is simple but effective technique for edge detection that greatly improves the performances of complicated images. The comparative analysis of various image edge detection methods is presented and shown that CA GoL based algorithm performs better than all these operators under almost all scenarios. The paper is organized as follows: CA is defined in section 2. Section 3 begins with a brief description of CA GoL and then goes on to propose a new method of edge detection with noise filtering based on CA GoL followed by the experimental results.

• II.    Cellular automata

CA model is composed of cell, state set of cell, neighbourhood and local rule. Time advances in discrete steps and the rules of the universe are expressed by a single receipt through which, at each step computes its new state from that of its close neighbours. Thus the rules of the system are local and uniform. There are one- dimensional, two-dimensional and threedimensional CA models. For example, a simple two-state, one dimensional CA consists of a line of cells, each of which can take value ‘0’ or ‘1’. Using a local rule (usually deterministic), the value of the cells are updated synchronously in discrete time steps. With a k-state CA model each cell can take any of the integer values between 0and k-1. In general, the rule controls the evolution of the CA model.

A CA is a 4-tuple {L, S, N, F}: where L is the regular lattice of cells, S is the finite state of cells, N is the finite set of neighbors indicating the position of one cell related to another cells on the lattice N, and F is the function which assigns a new state to a cell where F:S|N| S.

As the image is a two dimensional, here we use 2DCA model. In a 2DCA the cells are arranged in a two dimensional grid with connections among the neighboring cells, as shown in the figure (1). The central box represents the current cell (that is, the cell being considered) and all other boxes represents the eight nearest neighbours of that cell. The structure of the neighbours mainly includes Von Neumann neighbourhood and moore neighbourhood are shown in figure–(2):

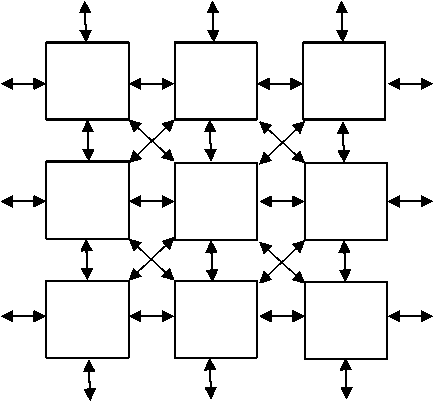
Figure (1): Network Structure of 2DCA

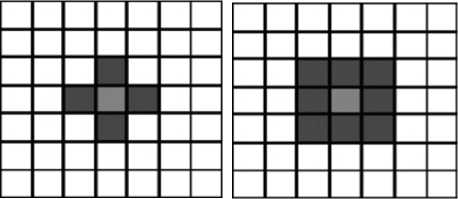
Figure (2) : structure of neighbourhoods

• (a)    Von Neumann neighbourhood

• (b)    Moore neighbourhood

Von Neumann neighbourhood, four cells, the cell above and below, right and left from each cell is called von Neumann neighbourhood of this cell. The radius of this definition is 1, as only the next layer is considered. The total number of neighbourhood cells including itself is five as shown in the equation (1)[10]:

N(I,j) = { (k,l) Є L : |k-i| + |l-j| ≤ 1 }             (1)

where, k is the number of states for the cell and l is the space of image pixels. Besides the four cells of von Neumann neighbourhood, moore neighbourhood also includes the four next nearest cells along the diagonal. In this case, the radius r=1 too. The total number of neighbour cells including itself is nine all as shown in the equation (2)[10]:

N(I,j) = { (k,l) Є L : max (|k-i|,|l-j|) ≤ 1 }         (2)

The state of the target cell at time t+1 depends on the states of itself and the cells in the moore neighbourhood at time t, that is:

S i,j (t+1) = f ( S i-1,j-1 (t) , S i+1,j (t) , S i-1,j+1 (t) , S i,j-1, S i,j (t) , S i,j+1 (t) , S i+1j-1 (t) , S i+1,j (t) , S i+1,j+1 (t) )    (3)

• III.    Game of life

John Horton Conway’s Game of Life [23][24] is a simple two-dimensional, two state cellular automaton (CA), remarkable for its complex behaviour [23][25]. That behaviour is known to be very sensitive to a change in the CA rules. Here we continue our investigations into its sensitivity to changes in the lattice, by the use of periodic boundary conditions for noise filtering and edge detection.

The bi-dimensional CA called the GoL was designed by Conway. It consists of an [M × N] matrix of cells, where each cell may take only two states: alive (represented by one) or dead (represented by zero). Each cell has eight neighbors, according to the Moore neighborhood. At every time step, also called a generation, each cell computes its new state by determining the states of the cells in its neighborhood and applying the transition rules to compute its new state. Every cell uses the same update rule, and all the cells are updated simultaneously.

As Figure (1.(b)) shows, “life-game” is a special cellular automata with two dimensions, determining the state of center cell in the next step according to the states of the neighborhood of it. In Figure (1(b)), center cell is colored with grey, neighborhood cells are colored with black. There are some characteristics about this pattern as follows [27].

• • . Cells are scatted in the grid.

• • . The cell has two states with 0 or 1, we can define state

0 as “dead” and state 1 as “live” and neighbourhood radius is set to 1.

• • . The eight cells adjacent to center cell is defined as neighborhood cells.

• • . A state of a cell depends on the states of its neighborhood cells and its state in the moment.

The next state of a cell is determined as follows:

• •    "Birth": A cell dead at time t becomes alive at time t+1

if exactly three of its neighbors are alive at time t.

• •    "Death by overcrowding": A cell alive at time t dies at time t+1 if four or more of its neighbors are alive at time t.

• •    "Death by exposure": A cell alive at time t dies at time t+1 if one or none of its neighbors are alive at time t.

• •    "Survival": A cell alive at time t will remain alive at time t+1 if two or three of its neighbors are alive at time

t.

Mathematically, the overall evolutions rules of the GoL can be described as follows:

• 1,    Sum=2,3

If St = 1, then St+1 =

0, Sum ≠2,3

• 1,    Sum = 3

If St = 0, then St+1 =

• 0,    Sum ≠ 3

Where, St is cell state at the t-0, St+1 and sum is the number of “live” cells in the eight neighborhood cells.

• IV.    proposed model

The following is the construction of CA model for edge detection and noise filtering:

At first we use the greyscale image f(x,y) for initial condition. Then calculate statistical data M and from data it is easy to find a bigger threshold value v. At the same time , we establish a matrix B[bi.j]m*n , where i=1,2,3,-------,m and j=1,2,3,------n

If mi,j>=v then bi,j =1

else

B i,j =0

Lattice geometry: two dimensional square lattice of size M*N.

Neighbourhood: moore’s neighbourhood with radius r=1

Boundary condition: periodic on all four sides, in order to avoid the boundary problem

Initial condition: the matrix B

State set: s={0,1}

To judge the edge point and non-edge point, the centre cell S^t i,j needs to meet the criterion of the CA GoL described in the above section.

Secondly, we take a binary image corrupted with “Salt and pepper Noise”. In order to remove the noise as well as detect the edges, we apply the same CA GoL rule. And from the experimental simulations we found that the results are more desirable than that of previously defined techniques. Also, we find more desirable results by changing the parameters of the CA GoL.

• V.    experimental results

The experimental image is selected as the classical Lena image and cameraman image, whose sizes are 256×256. Figure (3), figure (4) and figure (5), figure (6) shows the simulations of the proposed method based on CA GoL on the Lena image and Cameraman Image.

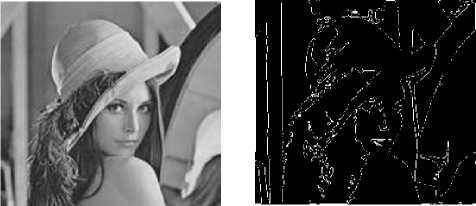
(a)                             (b)

Figure (3): CA GoL based Edge Detection without added noise

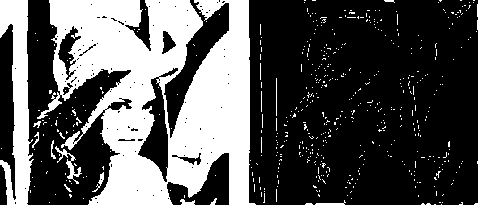
(a)                           (b)

Figure (4): CA GoL Based Edge Detection with Noise Filtering

Quality is assessed in two different ways: accuracy of edge detection, and level of connectivity in continuous edges. If some edges are still unconnected after edge detection, then an additional edge linking process is required. From the above results, we see that the edges obtained based on CA GoL are little weak. In order to enhance these edges, we change the parameters of CA GoL. Only by changing the “Survival” parameter of the CA GoL shows improvements over the standard game of life, while the other parameters does not change or improve the original image.

Figure (7) shows the simulations on the Lena image without added “Salt and pepper Noise”. Fig. (7.a) is the original image, figure (7.b) is the edge detected image obtained after applying CA GoL, whereas the figure (7.c)-figure (7.f) shows the results after changing the parameters of “Survival” state by fixing the sum between 1-5, 1-6, 1-7, 1-8. It is clearly seen that by changing the sum between 1-8 gives better edge detection.

Figure (8) shows the simulations on the Lena image added with “Salt and pepper Noise”. Fig. (8.a) is the original image, figure (8.b) is the edge detected image obtained after applying CA GoL, whereas the figure (8.c)-figure (8.f) shows the results after changing the parameters of “Survival” state by fixing the sum between 1-5, 1-6, 1-7, 1-8. Also its clearly seen that by changing the sum between 1-6 gives better edge detection whereas, by changing the sum between 1-7 and 1-8 produces some noise also.

Figure (9) shows the comparative results of the proposed method and the traditional methods of edge detection, whereas figure (9.a) is the original image, figure (9.b) is the image obtained after applying the proposed model, figure (79.c) is the edged image produced by the Sable method and figure (9.d) is the edged image produced by Canny method. It is clearly visible from the results that the proposed method is the best method than the traditional methods of edge detections.

(a)                              (b)

Figure (5): CA GoL based Edge Detection without added noise

(a)                              (b)

Figure (6): CA GoL Based Edge Detection with Noise Filtering

(a)

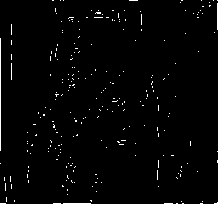
(b)

(e)

(f)

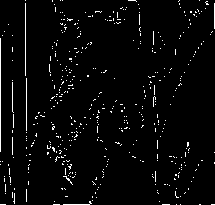
(c)

(d)

Figure (8): Simulation on Lena Image without added “Salt and Pepper Noise”.

(e)

(f)

Figure (7): Simulation on Lena Image without added “Salt and Pepper Noise”.

VI. CONCLUSION

In this paper we have propose a new method for edge detection with noise filtering based on CA GoL. Further, we investigate new rules base on CA GoL for edge detection with noise filtering that shows great improvements over the standard CA GoL. By experimental comparison of different methods of edge detection we observe that the proposed method leads to a better performance. The experimental results also demonstrated that it works satisfactorily for different digital images. This method has potential future in the field of digital image processing. The work is under further progress to examine the performance of the proposed edge detector with noise filtering for different digital images affected with different kinds of noise.

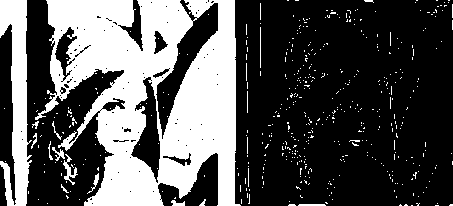
(a)                          (b)

(a)                             (b)

(c)                           (d)

(b)                            (d)

Figure (9): Comparative results on Lena, (a) original image, (b) edge image with Soble operator, (c) edge image with Canny method, (d) edge image with proposed method