Инженерная методика оценки несущей способности и ресурса конструкции с дефектом

Практически каждый изготовленный экземпляр изделия ракетно-космической техники, комплектуемый десятками тысяч деталей, имеет те или иные отступления от конструкторской документации, обусловленные различными причинами, наиболее распространенные из которых следующие: дефекты конструкционных материалов, несовершенство применяемых технологий, ошибки при изготовлении деталей, несоответствия при сборочных операциях, забоины, царапины, вмятины в результате несанкционированных воздействий и т. д. Достаточно часто возникшие несоответствия устранить сложно, иногда невозможно, при этом всегда их устранение связано с потерями времени и дополнительными затратами. В связи с этим весьма важно достоверно установить степень влияния несоответствий на обязательные характеристики конструкций, сохранение их работоспособности, функциональной пригодности, прежде всего, в аспекте надежности и безопасности эксплуатации изделия.

дефекты

Проблема производственных дефектов особенно актуальна для конструкций, изготавливаемых сваркой плавлением. К таким конструкциям относятся топливные баки двигательных установок, баллоны высокого давления, герметичные приборные отсеки, обитаемые отсеки космических кораблей и орбитальных модулей, трубопроводы. Эти конструкции являются не только основными составными частями любого космического объекта, но и важнейшими компонентами, определяющими надежное его функционирование, а в случае пилотируемого аппарата — обеспечение жизнедеятельности экипажа. Причем, для перечисленных выше конструкций необходимым условием является не только гарантия их прочности, но и сохранение герметичности на протяжении всего жизненного цикла изделия.

Сварные швы содержат множество разнообразных дефектов. Это непровары, поры, вольфрамовые, окисные, неметаллические включения, проплавы, кратеры, трещины, прожиги и др. Допустимость дефектов, их размеров, взаимного расположения регламентирована стандартами [1, 2]. Для силовых сварных конструкций обязательна заводская опрессовка — контрольные испытания каждого изготовленного экземпляра на прочность нагрузками не ниже эксплуатационного уровня. Упомянутые выше конструкции проходят также испытания на герметичность. В результате каждая изготовленная конструкция имеет экспериментальное подтверждение как прочности, так и герметичности на момент изготовления. Вместе с тем, современные автоматические космические аппараты разрабатываются, исходя из срока службы на орбите в течение 10–15 лет [3]. Не меньше срок эксплуатации модулей действующей Международной космической станции [4, 5]. Успешно выполняли летную программу многоразовые транспортные космические системы Shuttle и «Энергия–Буран». Космические корабли нового поколения разрабатываются с учетом обеспечения многократного запуска возвращаемого аппарата. Отсюда проистекают требования к достоверным оценкам и прогнозам поведения дефекта в условиях длительного воздействия эксплуатационных факторов в течение жизненного цикла изделия.

задачи

Важной особенностью изделий ракетно-космической техники являются невозможность ремонта в процессе эксплуатации для ракет-носителей и автоматических аппаратов, и значительные трудности — для пилотируемых объектов. При этом научно-технические наработки, ориентированные на другие отрасли, нормативные принципы, действующие в других отраслях, в т. ч. в авиационной промышленности, не могут быть перенесены в ракетно-космическую отрасль без существенной коррекции, что обусловлено специфическими особенностями конструкций и условий их эксплуатации: высоким уровнем нагружения, комбинированным воздействием факторов в широком амплитудном и частотном диапазонах, доминирующим принципом минимизации массы. Причем, как правило, главным условием в оценке и критерием принятия решения является не прочность, а герметичность, т. е. задачей расчета является прогноз ресурса не до разрушения, а до потери герметичности из-за прорастания на всю толщину оболочки усталостной трещины, образовавшейся из несквозного дефекта или совокупности дефектов. Изложению принципов и подхода к разработке такой инженерной методики расчета посвящена настоящая статья.

Составные части методики

Процесс оценки ресурса конструкции с производственным дефектом охватывает различные сферы деятельности инженерного состава научно-технического предприятия и, соответственно, складывается из следующих составных частей:

• •    выявление дефекта, определение его параметров, расположения и ориентации;

• •    расчет нагрузок для всего жизненного цикла изделия;

• •    определение условий эксплуатации изделия для расчетных случаев;

• •    определение характеристик конструкционных материалов для всех условий эксплуатации;

• •    расчет напряженно-деформированного состояния конструкции для всех расчетных случаев;

• •    формирование критерия критического состояния;

• •    расчет поведения дефекта и оценка условий достижения критического состояния.

Каждая из составляющих является самостоятельным направлением, и поставленная задача предусматривает выполнение соответствующей части на уровне, который в настоящее время обеспечивают возможности технологий, оборудования, вычислительной техники и программных продуктов.

характеристики дефекта

Классификация дефектов сварных соединений приведена в отраслевом стандарте [2]. Она охватывает швы, полученные плавлением и контактной сваркой. Для выявления дефектов разработано множество методов, наиболее распространенные и освоенные из которых — радиографический, ультразвуковой, капиллярный, магнитопорошковый. Применение методов неразрушающего контроля регламентировано стандартами [6–9]. Оставшиеся после устранения недопустимых в соответствии с нормативной документацией дефекты должны быть зафиксированы, при этом отмечаются их величина, расположение и ориентация. По той же схеме фиксируются для особого рассмотрения неразрешенные нормативной документацией, но неустранимые по тем или иным причинам дефекты, а также несоответствия, имеющие другое происхождение. В случае, если неразрушающие методы контроля не выявили дефектов, их начальный размер назначается в соответствии с границей чувствительности примененного метода, а расположение и ориентация считаются произвольными, обеспечивающими наибольшую предрасположенность к росту при имеющем место поле напряжений.

Для дальнейшего схематизируем начальный дефект, считая его трещиной с размером l , расположенной в поле равномерного плоского напряженного состояния σ и ориентированной относительно главных напряжений σ = σ ₁ в соответствии с рис. 1.

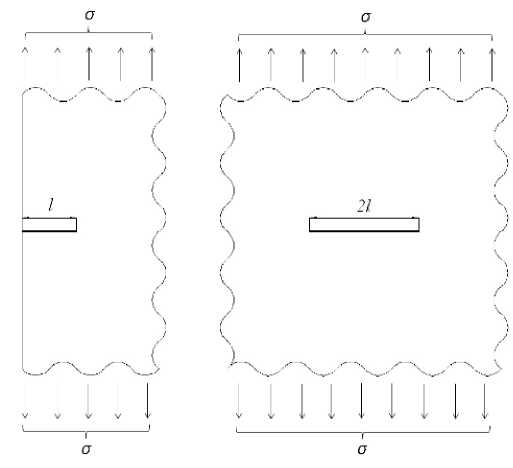
Рис. 1. Схематизация дефекта

Поскольку радиус в вершине трещины стремится к нулю, и решения сингулярных уравнений равновесия в этой особой точке стремятся к бесконечности, в механике хрупкого раз- рушения введено и стало основным понятие «коэффициент интенсивности напряжений» K = σ πl .

Численное значение K (или K1 для плоского напряженного состояния) характеризует состояние дефекта и склонность его к росту в условиях эксплуатации конструкции. Множество исследований и публикаций, начиная с середины прошлого века, посвященных кинетике усталостной трещины, трещино-стойкости, сопротивлению хрупкому и квазихрупкому разрушению, свидетельствует не столько об актуальности проблемы, сколько о трудности обобщения результатов и распространения их на достаточно большую область материалов и конструкций. Это обусловлено принципиально различным поведением различных материалов, более того — одного и того же материала при различиях в его структуре, а материала одной и той же структуры — при различных температурах, под действием различных нагрузок и их сочетаний при наличии разных дефектов. В связи с этим задачу корректного прямого расчетного определения ресурса имеет смысл ставить только в исключительных случаях. Она должна содержать разработку конечноэлементной модели конструкции с акцентом на воспроизведение зоны дефекта, достоверные сведения о характеристиках материалов с учетом их структурных особенностей и эксплуатационных условий. Расчет должен проводиться на мощном программном комплексе уровня NASTRAN или ANSYS с привлечением вспомогательных программных продуктов. В процессе расчета должно быть смоделировано, с учетом хронологической последовательности, воздействие на конструкцию всех нагрузок полного жизненного цикла изделия в совокупности с другими эксплуатационными воздействиями, прежде всего температурой. В результате будет получена исчерпывающая картина кинетики дефекта, но достоверность и точность результата не может быть выше достоверности и точности исходных посылок, заведенных в модель: характеристик дефекта, свойств конструкционных материалов, спектра нагрузок с амплитудными значениями и количеством циклов каждого уровня, эксплуатационных условий.

Механика разрушения изначально формировалась с ориентацией на хрупкие материалы. При идеально хрупком разрушении пластическая зона у вершины трещины отсутствует. Пороговое значение параметров, при котором начинается рост трещины, совпадает с прогнозом на основе критериев линейной механики разрушения [10, 11]. Удовлетворительный прогноз начала роста трещины линейная механика дает и при квазихрупком разрушении, когда у вершины трещины формируется локальная пластическая зона. При вязком разрушении пластические деформации распространяются на всю зону трещины, при этом контур ее вершины скругляется. Начало роста трещины прогнозируется на основе критериев нелинейной механики разрушения [12–14].

напряженно-деформированное состояние

Уровень напряжений имеет определяющее значение как для старта трещины, так и дальнейшего ее поведения. При этом необходимым условием роста трещины является либо монотонное возрастание нагрузки, либо, при фиксированном значении максимальной нагрузки, наличие переменной составляющей определенного уровня. Для расчета напряженно-деформированного состояния необходимы значения перегрузок для всех расчетных случаев, соответствующие им условия эксплуатации, в первую очередь — температурные режимы, а также механические характеристики материалов. Диаграмма σ–ε должна заводиться в расчет с учетом сложного напряженного состояния. Расчет напряженно-деформированного состояния в настоящее время проводится практически всегда методом конечных элементов с применением универсальных программных комплексов, наибольшее распространение из которых получили NASTRAN и ANSYS. В случае высокоградиентных температурных полей, особенно циклически меняющихся по времени, необходим расчет температурных напряжений. Поскольку скорость роста трещины при циклическом нагружении зависит от размаха переменной составляющей напряжений, а ресурс — от числа циклов их действия, формируется блок напряжений, состоящий из спектра напряжений с различными значениями амплитуд, коэффициентов асимметрии и числа циклов действия (рис. 2).

Для дальнейшего целесообразно привести все напряжения к единому стандартному виду: симметричному или пульсирующему циклу. Можно рекомендовать для этого формулу Одинга [15], наиболее употребительную на практике и часто цитируемую в специальной литературе:

σ _–1 = σ _a ( σ _m + σ _a ) ;

σ0 = 2σa(σm + σa), где σ–1 — значение напряжений эквивалентного симметричного цикла; σ0 — значение напряжений эквивалентного пульсирующего цикла.

Следующим действием осуществляется приведение циклов к единому (наибольшему) или нескольким уровням. Приведение выполняется в соответствии с усталостной кривой, что предпола-

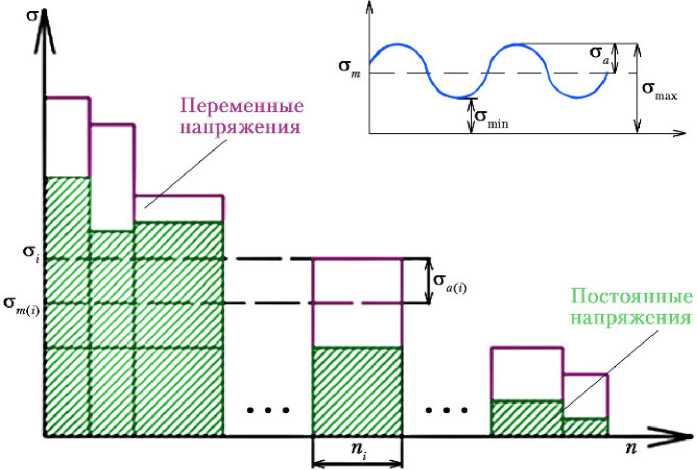
Рис. 2. Блок напряжений напряжений;

амплитуда переменной составляющей напряжений:

Примечание. r — коэффициент асимметрии цикла; σ _m — среднее значение

гает эквивалентность повреждаемости. Количество нагружений в эквивалентном цикле при линейном суммировании повреждаемости определяется по формуле

m n = Ё экв    i = ]

σ i

α

σ а

—

с пр

n ,

где nэкв — количество нагружений; σпр — амплитудное значение напряжений в эквивалентном цикле; σi — амплитудное значение приведенного напряжения i-го цикла; ni — количество нагружений

σ min r =       ; σ =

σm max

max min

2       ^{; σ a}

=

max min

.

в i -ом цикле.

Показатель кривой усталости α , как правило, принимается равным четырем, если о нем нет более достоверных сведений.

Если диапазон изменения амплитудных значений напряжений настолько велик, что составляющие блока располагаются по обе стороны от точки излома кривой усталости, то для каждой из двух частей следует принимать свое значение показателя степени α . Точка излома размещается между пределом пропорциональности и пределом текучести материала. Физический смысл ее заключается в появлении остаточных деформаций и петли гистерезиса при циклическом нагружении в левой от точки излома области кривой усталости (рис. 3).

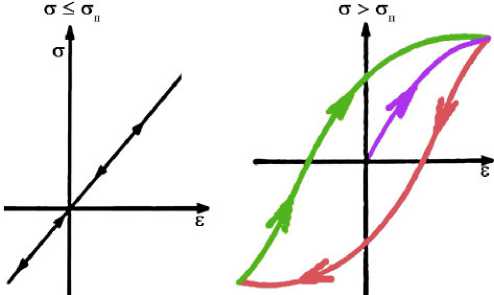
а) б)

Рис. 3. Деформирование: а — упругое; б — упругопластическое: ■ — первичное нагружение; ■ — разгрузка; ■ — вторичное нагружение

Выбор между симметричным и пульсирующим циклами целесообразно осуществлять в зависимости от располагаемых данных о свойствах конструкционного материала. В качестве рекомендации, основанной на опыте и экспериментах, можно рекомендовать значение α , равное четырем, для левой части кривой, и α , равное восьми — для правой. Необходимо подчеркнуть, что для достоверного подтверждения значений α необходимы эксперименты с соответствующим конструкционным материалом, конкретным сортаментом (лист, плита, профиль, штамповка и т. д.), конкретным состоянием (отожженное, нагартованное, закаленное) и, конечно, для сварных швов. Для примера на рис. 4 приведена типичная кривая усталости для алюминиевого сплава.

Приведение количества циклов с переходом в другую часть диапазона (переходов через точку излома) должно осуществляться, естественно, в два приема: до точки излома с одним значением α , после — с другим.

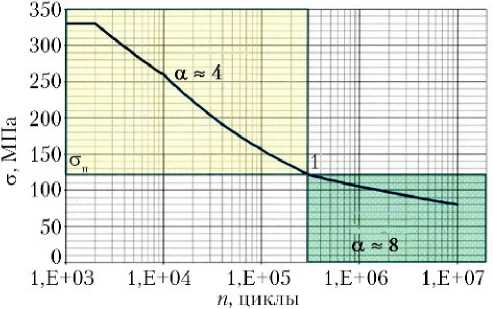
Рис. 4. Кривая усталости. 1 — точка излома кри- вой усталости

Следует отметить также, что скорость роста трещины dl/dn как функция размаха коэффициента интенсивности напряжений Δ K параметрически зависит от уровня напряжений σ . Поэтому приведение блока напряжений целесообразно осуществлять к значению σ _пр, по которому имеются или определяются экспериментальные данные для соответствующего материала.

коэффициент интенсивности напряжений

Ключевым параметром, на котором базируются критерии механики разрушения, является коэффициент интенсивности напряжений K . Начало изучения процесса разрушения восходит к основополагающей публикации Гриффитса [16] в 1920 г., в которой рассмотрена плоская задача теории упругости: равномерное растяжение с напряжениями σ пластины с эллиптическим вырезом (рис. 5).

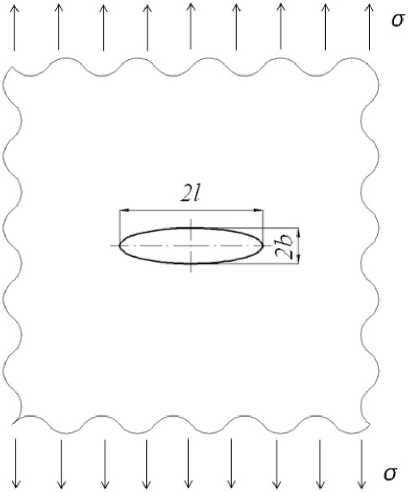
Рис. 5. Задача Гриффитса

Решая задачу энергетическим методом при значении поперечной полуоси эллипса, стремящемся к нулю ( b → 0), Гриффитс получил формулу

2 E γ

σ ² =            = const,

π l (1 – ν ²)

где Е — модуль упругости; ν — коэффициент Пуассона; γ — некоторая константа материала, названная плотностью поверхностной энергии.

Таким образом, коэффициент интенсивности напряжений

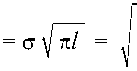
2 E γ

(1 – ν ²)

= const

является определяющим параметром, характеризующим конструкционный материал в аспекте трещиностойкости. Экспериментальное подтверждение Гриффитс получил опытами со стеклом.

Для пластичных материалов имеют место значительные количественные отклонения. В пятидесятые годы XX века Орован [17] и Ирвин [18, 19] ввели понятие γ _р — работа пластической деформации при образовании единицы поверхности.

Формула Гриффитса приняла вид:

σ ² =

^{2 E ( γ + γ p )} π l (1 – ν ²) ^.

Коэффициент интенсивности напряжений

K = σ π l =

2 E ( γ + γ _p )

(1 — V 2 )

= const.

Учитывая, что для пластичных материалов γ _р на несколько порядков больше γ (для стали γ _р ≈ 1 000 γ ), легко понять и количественно оценить, насколько трещиностойкость у пластичных материалов выше, чем у хрупких.

Актуальность проблемы обусловила обилие исследований и публикаций по теории хрупкого и квазихрупкого, а в последнее время и вязкого разрушения. Наиболее системное изложение теоретических основ линейной механики разрушения можно найти в книгах [10, 11]. Представление о современном состоянии и проблематике науки о трещинах и разрушении можно почерпнуть из монографии [20].

критерии разрушения

Основным параметром, характеризующим прочность материала или конструкции, являются напряжения σ , τ или, точнее, тензор напряжений

T

σ

σ 1	τ 12
τ 21	σ 2
τ 31	τ 32

^τ 13

^τ 23     ^.

σ ₃

Механические характеристики материала ( σ _В, τ _В, σ _Т, τ _Т) определяются, как правило, простыми нагружениями образцов: одноосным растяжением, сжатием, кручением, изгибом. Затем определяется склонность материала в его структурном состоянии к тому или иному виду разрушения, и выбирается для него теория прочности, которая соответствует сложному напряженному состоянию. Критерии прочности, а также текучести для различных теорий формируются из компонентов тензора напряжений. Исчерпывающую информацию о многочисленных критериях прочности можно получить из книги [21], там же приведена обширная библиография по этой тематике.

Критерии разрушения формируются как функции трех коэффициентов: Р = f ( K _I, K _II, K _III), где K _I = σ π l ;

K _II = τ ₁₂ π l ; K _III = τ ₁₃ π l .

Для трещин основных типов критерий разрушения имеет вид:

• •    нормальный разрыв K _I = K _{I C} , K _II = K _III = 0;

• •    поперечный сдвиг K _II = К _{II C} , K _I = K _III = 0;

• •    продольный сдвиг K _III = К _{III C} , K _I = K _II = 0.

Здесь K _{I С} , K _{II С} , K _{III С} — важнейшие константы материала, предельные значения коэффициентов, определяющие его трещиностойкость. Величина K _{I C} называется вязкостью разрушения. В дальнейшем изложении приводятся выкладки, касающиеся только представляющих наибольший интерес трещин разрыва. Экспериментальное определение вязкости разрушения сопряжено со значительными трудностями. Применяемые на практике методы делятся на три группы:

• •    методы, использующие корреляцию вязкости с другими характеристиками материала, определение которых более доступно;

• •    прямые методы измерения необратимой работы γ _р ;

• •    методы, основанные на решении конкретных задач механики разрушения.

Следует отметить обилие факторов, влияющих на критерии разрушения [10, 11, 22], а также многочисленные попытки различных авторов уточнить эти критерии [10, 11, 13, 23].

разрушение

Процесс разрушения возможен двух видов:

• •    при статически действующей монотонно возрастающей нагрузке;

• •    при циклически повторяющейся нагрузке.

При статически действующей нагрузке более явно проявляется различие в характере разрушения хрупких и пластичных материалов. Если известен начальный размер дефекта (трещины) l _н и критическое значение коэффициента интенсивности напряжений K _{I C} , то из формулы

KI = σ πl следует, что величина разрушающих напряжений в зоне трещины играет следующая константа материала KV [10], соответствующая пределу усталости материала. Значение KV лежит в пределе 5…10% от KIC и является точкой старта усталостной трещины. То есть, при KI ≥ KV при переменной нагрузке возможно начало роста трещины. Условие зависимости скорости роста трещины от переменной составляющей коэффициента интенсивности напряжений впервые сформулировано в работе [24], и затем получило экспериментальное подтверждение в многочисленных публикациях [10]. В соответствии с этим условием, скорость роста трещины является функцией удвоенной амплитуды (размаха) коэффициента интенсивности напряжений, т. е.

dl

= f ( Δ K _I).

Известны различные зависимости для скорости роста трещины, например, формула Пэриса [10]

dl

= G ₀( K _Imax – K _Imin)⁴, dn

σ

p

^K I C

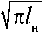
где G ₀ — постоянная материала; формула Черепанова [10]

То есть, до достижения нагрузкой величины, обеспечивающей в окрестности дефекта напряжения уровня σ _р , трещина в хрупком материале никак себя не проявляет. При достижении напряжениями значений σ _р происходит лавинообразное разрушение, ибо равновесное состояние с трещиной большего размера возможно только при соответствующем уменьшении напряжений, т. е. нагрузки.

При квазихрупком разрушении пластичного материала действует та же формула для разрушающих напряжений, но процесс разрушения будет заметно отличаться от хрупкого. Вначале в углах трещины появятся расширяющиеся зоны пластических деформаций. Углы трещины притупляются и скругляются, раскрытие трещины увеличивается. При достижении напряжениями значения σ _р трещина переходит в неустойчивое состояние, и происходит лавинообразное разрушение.

При KI < KIC и статически приложенной нагрузке трещина не растет. При циклически повторяющейся нагрузке важную роль dl dn

K ²   – K ² + ln ^{K I2 C – K I2max}

Imax Imin           _{2       2}

KIC – KImin где β — постоянная материала.

При использовании любой формулы необходимо экспериментальное определение констант материала, определяющих скорость распространения трещины. Характерная экспериментальная кривая для алюминиевого сплава приведена для примера на рис. 6.

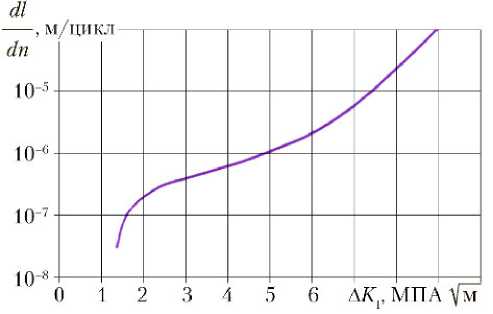
Рис. 6. Зависимость скорости роста трещины от размаха коэффициента интенсивности напряжений

В зависимости от максимального значения напряжений и критического значения коэффициента интенсивности напряжений из формулы

KIC = σmax πlк определяется критическая длина трещины l =     IC

к

πσ ²

max

.

Для достижения критической длины необходим рост трещины на величину

Δ l _к = l _к – l _н.

Поскольку циклы действующих напряжений остаются неизменными, Δ K _I = ξ изменяется с ростом трещины от начального значения

ΔK (Iн) = Δσ πlн до конечного

_{Δ K} ( _I к) ₌

Δσ π l _к .

Определив на промежутке {ΔK (Iн), ΔK (Iк)} среднее значение скорости роста трещины dl

U<к> = —, ср dn можно найти число циклов нагружения N, необходимое для выращивания трещины до критического значения:

_N (к) ₌

∆l к Uj^ ■ ср

Если требуется определить количество циклов до достижения длиной трещины определенного промежуточного значения l_n , например, нарушающего герметичность,

Δln = ln – lн, то определяются соответствующие значения коэффициента интенсивности напряжений

ΔK(n) = Δσ πl , I                  n осредненной скорости роста трещины на промежутке {ΔK (Iн), ΔK (Iк)} dl

U(р1) = — с р dp и количество циклов нагружения, необходимое для выращивания трещины до величины l n

∆ l

N(n) =       • ср

При необходимости рассчитать размер трещины после определенного промежуточного числа эквивалентных циклов нагружения Nn, длина ln находится по формуле ln = lн + Δln.

Приращение длины проще всего рассчитывать методом последовательных приближений. Исходя из осредненной скорости развития трещины U _c ⁽ n ) , определяется приращение

А l n = U ( P ^p >  N n .

Исходя из значения Δln, вычисляется значение размаха коэффициента интенсивности напряжений ΔKnI, соответствующее концу промежутка изменения аргумента ΔKI. Далее Δln находится во втором приближении интегрированием фактической функции скорости на промежутке {ΔK (Iн), ΔK (Iк)} ак| p)

Δ l_n = ∫ U ( ξ ) d ξ .

A K (н)

Если значение Δ l_n существенно отличается от полученного в предыдущем приближении, процедура вычислений повторяется. Итерационный процесс прекращается при получении требующейся точности.

обсуждение результатов

Построенная на основе критериев механики разрушения методика расчета конструкций с дефектом содержит целый ряд упрощающих допущений, дающих возможность ее использования в инженерной практике. Наиболее серьезные из них, оказывающие влияние на точность результатов, следующие:

• •    схематизация дефекта с представлением его трещиной, расположенной в плоскости главных напряжений;

• •    допущение о равномерности в зоне дефекта поля нормальных напряжений с плоским деформированием;

• •    приведение нагрузок и напряжений к одинаковому циклу с единым коэффициентом асимметрии;

• •    приведение блока нагрузок к одноуровневому единому амплитудному значению;

• •    выбор простейшего критерия разрушения;

• •    исключение из рассмотрения дополнительно влияющих факторов и условий

эксплуатации: температура, среда, электромагнитное излучение, динамическое воздействие нагрузок и др.;

• •    допущение об изотропности материала.

Необходимо отметить, что современный уровень развития вычислительной техники, функционирующие программные комплексы позволяют моделировать процесс развития трещины с высоким уровнем достоверности. Модель объекта при этом может быть построена с любой степенью подробности в окрестности дефекта, а сам дефект в его начальном виде схематизирован и встроен в модель. Могут быть воспроизведены все условия эксплуатации, а весь жизненный цикл изделия сымитирован полным набором реально действующих нагрузок во всех их сочетаниях и хронологической последовательности. Свойства материала с учетом его состава, структуры, условий эксплуатации, особенностей деформирования позволяют не только корректно воссоздать напряженно-деформированное состояние конструкции под действием нагрузок, но и получить кинетику трещины в процессе эксплуатации изделия. Постановку и решение задачи в таком виде можно себе представить как редкое исключение, и для ее реализации необходимы качественное улучшение методов и средств неразрушающего контроля, конкретизация и синхронизация условий эксплуатации, включая нагрузки, создание всеобъемлющей и достоверной базы данных по конструкционным материалам во всем их многообразии. Определенные сложности моделирования дефекта связаны с сингулярностью уравнений статики сплошной среды или уравнений теории пластин и оболочек, ибо основные процессы развиваются как раз в окрестности особых точек, каковыми являются вершины трещины.

Внедрение изложенной методики также требует увеличения объема и улучшения качества неразрушающего контроля с документальным фиксированием его результатов, повышения точности определения и документирования нагрузок в совокупности с уточнением условий эксплуатации при их действии и, главное, увеличение перечня, объема, качества и достоверности экспериментального определения свойств конструкционных материалов. Помимо общеизвестного набора механических характеристик, необходимы

• •    диаграммы σ – ε ;

• •    критерии прочности и пластичности;

• •    кривые усталости σ – N ;

• •    диссипативные свойства;

• •    критические значения коэффициентов интенсивности напряжений K_С ;

• •    функции скорости роста трещин в зависимости от размаха коэффициента

интенсивности напряжений:    = f ( Δ K _I).

dn

Всю совокупность выполняемых в рамках предлагаемой методики действий можно разбить на шесть блоков, а общую комплексную задачу — соответственно, на шесть составляющих, взаимосвязанных задач.

Блок моделирования объекта.

Задача 1: разработать конечноэлементную модель конструкции, включая геометрию, граничные условия, упругопластические характеристики конструкционного материала с учетом его состояния, структуры, условий эксплуатации и типа напряженно-деформированного состояния.

Блок контроля качества изготовления.

Задача 2: определить несоответствия и дефекты изготовленной детали; неустранимые несоответствия документировать с указанием их вида, расположения, размеров.

Блок моделирования нагрузки.

Задача 3: разработать модель воздействий, т. е. определить нагрузки, действующие на конструкцию, синхронизировать их между собой и с другими условиями эксплуатации (температура, среда, излучения и т. д.); построить блок нагружения за весь жизненный цикл изделия.

Блок расчета напряженно-деформированного состояния.

Задача 4: определить напряженно-деформированное состояние детали, построить на основе закона суммирования повреждений и кривой усталости блок напряжений, определить параметры напряжений эквивалентного цикла и количество их действия.

Блок прогноза ресурса.

Задача 5: рассчитать на основе критериев механики разрушения поведение начального дефекта в детали (задача 1 ) с дефектом (задача 2 ) из материала со свойствами (задача 6 ), под действием нагрузок (задача 3 ), в условиях напряженно-деформированного состояния (задача 4 ).

Блок характеристик материала.

Задача 6: экспериментально определить и документировать характеристики, необходимые для решения:

задач 1, 3, 4: диаграммы σ – ε для различных видов напряженного состояния;

задачи 4: закон накопления усталости повреждений и кривой Велера (усталости);

задачи 5: критические значения коэффициента интенсивности напряжений, скорость роста трещины.

Таким образом, комплексная задача оценки ресурса решается в следующей последовательности:

• •    разработка конечноэлементной модели конструкции;

• •    определение вида, расположения и размеров начального дефекта;

• •    построение блока нагружения конструкции с учетом условий эксплуатации;

• •    расчет напряженно-деформированного состояния, определение параметров эквивалентного цикла переменных напряжений и количества их действий;

• •    прогноз поведения начального дефекта в соответствии со свойствами материала и критериями механики разрушения.

Необходимо отметить следующие очевидные соображения:

• •    достоверность решения общей задачи не может быть выше достоверности решения входящих в нее составляющих задач;

• •    точность решения задачи зависит от точности исходных посылок;

• •    достоверность оценки ресурса напрямую влияет на надежность функционирования конструкции;

• •    для пилотируемых полетов достоверность оценки ресурса влияет на безопасность экипажа.

Из сказанного следует, что обеспечить необходимую достоверность оценки ресурса и повысить ее точность можно только в результате повышения точности решения всех составляющих задач. Современный уровень вычислительной техники и программных продуктов обеспечивает практически любую точность результатов расчетных работ. Поэтому для получения надежных оценок ресурса в первую очередь необходимо обеспечение базы данных по свойствам наиболее часто применяемых конструкционных материалов, прежде всего, свариваемых сплавов. Параллельно с базой данных самостоятельную практическую ценность представляет частная задача разработки структуры унифицированной модели конструкционного материала, содержащей все перечисленные выше свойства, а также алгоритмизация встраивания модели в комплексную задачу расчета прочности и ресурса.

В работе [25] с применением приема, названного пошаговой дискретизацией многоуровневого динамического моделирования, показана картина развития динамических процессов в конструкции космического корабля вдоль его оси при ударном воздействии отсечки тяги маршевого двигателя ракеты-носителя. Анализ прочности всей конструкции выявил отсек, раму, деталь и, наконец, точку детали, которая является потенциальным очагом начала разрушения. В нашем случае решается в некотором роде обратная задача: в известной точке исследуется поведение дефекта в зависимости от всего комплекса воздействий на изделие. Естественно, что совпадение этих точек чревато самыми неприятными последствиями. И наоборот, расположение дефекта вне зоны влияния внешних воздействий не скажется на работоспособности конструкции.

Тестовой комплексной задачей для изложенной методики, решение которой, кроме того, остается актуальной и представляет самостоятельный практический интерес, может служить оценка ресурса конструкции бака окислителя последней ступени ракеты-носителя. Постановка этой задачи изложена в статье [26]. Объектом рассмотрения является верхнее днище бака, точнее — завершающий изготовление корпуса замыкающий сварной шов установки тоннельной трубы. Оценка должна проводиться для всего жизненного цикла корпуса бака, включая изготовление, заводские испытания, межцеховую транспортировку, транспортировку в составе ракеты-носителя с завода-изготовителя на технический комплекс, сборочные операции по ракете космического назначения, транспортировку в составе ракеты космического назначения на стартовый комплекс, заправку бака жидким кислородом, наддув, полет участка выведения. При этом должны быть учтены температурные условия эксплуатации: жидкий кислород в качестве компонента топлива и горячий «кислый» газ наддува. Внешние нагрузки, включая вибрации, должны быть синхронизированы с давлением и температурными полями с учетом их флуктуации. Уровень напряженного состояния в зоне дефектов сварного шва должен учитывать соответствующее повышение в связи с искажением реальной геометрии оболочки при сварке [26–28].

выводы

• 1.    Разработанная методика решения комплексной задачи оценки несущей способности и ресурса дает возможность путем решения последовательности частных задач дать оценку степени влияния характерных дефектов на прочность, герметичность, ресурс конструкции в условиях ее эксплуатации.

• 2.    Алгоритм решения комплексной задачи предусматривает:

• •    разработку конечноэлементной конструкции;

• •    определение вида, расположения и размеров дефекта;

• •    построение блока нагружения;

• •    расчет напряженно-деформированного состояния;

• •    прогноз поведения начального дефекта.

• 3.    Внедрение разработанной методики расчета конструкций с дефектом сыграет важную роль в повышении достоверности расчетов прочности и ресурса, в обеспечении надежности и безопасности эксплуатации изделий ракетнокосмической техники.

• 4.    Для внедрения методики в практику инженерных расчетов необходимо проведение масштабной работы по экспериментальному определению критериальных констант и свойств материалов с позиций линейной механики разрушения.