Инженерные формулы для определения постоянной времени

При теплотехнических расчетах часто необходимо знать, через какое время после начала процесса распределение температуры можно считать регулярным, а также с какого момента процесс можно считать установившимся. Характеристикой процесса, с помощью которой можно определить это время, является постоянная времени.

Постоянной времени считается число Т в представлении решения уравнения теплопроводности в виде ряда, получающегося при решении задачи методом Фурье:

г(х,т) = ф(х) +^е ^q?!(х) + А2е Г2ф2(х)+..., (1) где z(x,t) - температура в точке с пространственной координатой х в момент времени т; Ф! (х), ф2 (х),... - собственные функции соответствующей задачи Штурма-Лиувилля; ф(х) - распределение температуры, которое установится в пределе при т -^ оо. Для нахождения постоянной времени Т следует найти наименьший положительный корень ц характеристического уравнения, после чего постоянную времени можно найти по формуле где I - толщина пластины, а - коэффициент температуропроводности.

Зная постоянную времени, можно сказать с какого времени процесс можно считать регулярным, то есть удовлетворительно описанным толь ко первыми двумя членами в разложении (1). Действительно, через время Т второй член в выражении (1) уменьшится в е «2,7 раза. В рассматриваемых здесь простых задачах второй корень характеристического уравнения по крайней мере в два раза больше первого корня ц; показатели в экспонентах обратно пропорциональны квадратам характеристических чисел. Это означает, что третий член через время Т уменьшится по крайней мере в е4 « 55 раз. Поэтому на практике можно считать, что через время Т процесс становится регулярным. Через время ЗТ первая экспонента в выражении (1) уменьшится в е3«20 раз, следующие члены ничтожно малы, и процесс можно считать установившимся.

Характеристическое уравнение может быть трансцендентным и довольно сложным. Хотя при нынешнем развитии вычислительной техники, решить это уравнение нетрудно, неплохо иметь для этого простые приближенные формулы. В данной статье выводятся такие формулы для простейших задач теплопроводности.

Постановка задачи

Для неограниченной пластины (теплоизолированного с боков стержня, стены) распространение тепла описывается уравнением

St 82t    _,

—0<х,(3)

8т 5т²

начальным условием

?(х,0) = <р(х)(3.1)

и одним из краевых условий на поверхности пластины, например, при х = / :

/(Z,t) = /_b - первого рода.

Ot, х

^(^т/= ^ ” ВТОРОГО Р°Да>

(3.2)

Х-— (/,т) = а-(г_в -/(/,т)) -третьегорода.(3.4)

Ох

Аналогичные условия ставятся и при х = 0. Здесь I - толщина пластины (стены), а - коэффициент теплоотдачи, X - коэффициент теплопроводности материала пластины (стены), t^ - температура внешней среды, q - тепловой поток. Для характеризации условий третьего рода примеси/ няют безразмерный критерий Био: Bi = —.

Краевые условия I и III рода

Предположим, что в задаче (3) заданы краевые условия первого и третьего рода. В этом случае характеристическое уравнение [1, 2] запишем в виде

HCtg(n) = -Sz. (4)

Будем считать наименьший положительный корень этого уравнения функцией критерия Био: ц = ц(5/), О < Bi < оо , причём, ц(0) и р(°о) полагаем равными предельным значениям. Поскольку в формуле (2) для постоянной времени участвует множителем выражение 1/р2, то введём функ цию ц2(^0 = —?---Функция МгС^О убывает Р (Bi)

от — до —. Её график (рис. 1) похож на график л2л дробно-рациональной функции, поэтому будем искать приближение для ц2(^0 ввВДе

/ ,х ABi + В.

M(Bi) =-------,(5)

V 7 Bi^C где три параметра А, В, С нужно найти.

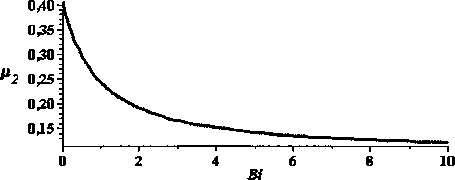
Рис. 1. График функции р2

Естественно потребовать совпадения функций р₂(^0 ^и M(Bi) при Bi-Q и Bi = оо, что даёт

В   4   ,1 равенства — = —, А = —. Тогда приближение С п л приобретает вид v ' it2 (Bi+С)

Для определения параметра С приравняем производные функций ц₂(^0 и M(Bi) при Bi = O:

32     3                Зл2 т ,

—- = ——, откуда С =--. Теперь функция л4    л2С             32

M(Bf) полностью определяется:

V 7 л2(в/+3л2/32)

График относительной погрешности „(»■)«(»)

приведён на рис. 2.            -

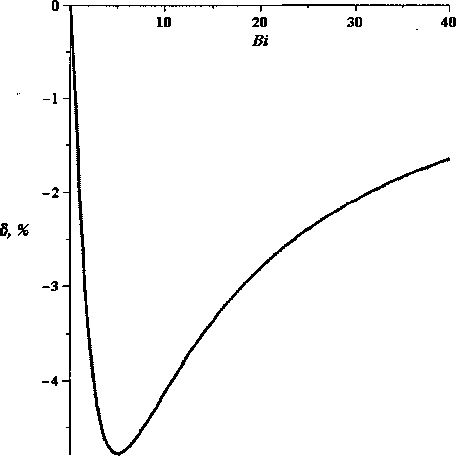
Рис. 2. Относительная погрешность формулы (7)

Из графика видно, что приближение одностороннее, т. е. М(В^>ц₂(В^ и, используя формулу (7) для определения постоянной времени, получаем приближённое значение с избытком, но не более 5 %. При выводе этой формулы мы использовали простые и вполне очевидные условия. Для применения запишем формулу (7) в виде

0,10135/+ 0,3750

Bi + 0,9255

Может оказаться, что 5 % - большая погрешность. Выведем формулу с меньшей погрешностью. Для этого поставим задачу: подобрать значения параметров А, В, С в формуле (5) так, что бы достигался минимум максимальной относительной погрешности при всех значениях Bi, то есть найти

Для решения этой задачи есть алгоритм Ремеза [3], применив который, получаем формулу

Васильев Ю.С., Донская А.Б.

Инженерные формулы для определения постоянной времени

m(5/) = °’^15/+0’³³⁶⁵,               (10)

v 7 Sz + 0,8193

относительная погрешность которой составляет 1,4 %. Это видно из графика на рис. 3.

В          ТЕ²

~ = 0, А = — . Тогда получим приближение в виде

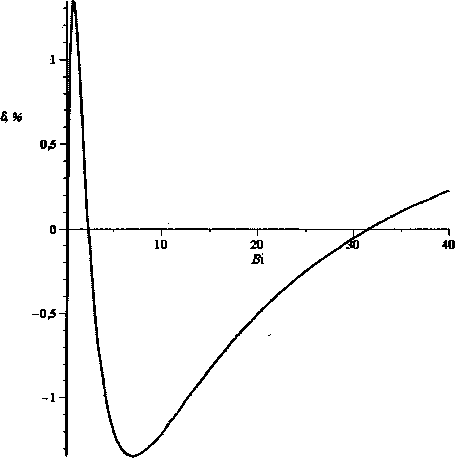
Рис. 3. Относительная погрешность формулы (11)

<12)

Неизвестный параметр С найдем из условия равенства производных функций p₂(#z) и M(Bi)

при Bi = 0 : 1 = —, откуда С = —. Таким обра зом, получим функцию М(Вг):

м^=^У±          (13>

.          Bi + Tr/4

• Так как в формуле (2) для постоянной време-1

ни участвует выражение —, то введем функцию

ц₃ (Bi) = — . Приближением для функции р₃ (Bi)

будет функция М₂ (Bi) = ^^.j ’ ^т- ^е-

М2 (Bi) =

Bi + 7t²/4

Bz-te2/4 *

По сравнению с формулой (8) погрешность при стремлении Bi к нулю или бесконечности увеличивается.

Краевые условия II и III рода

Пусть в задаче (3) заданы краевые условия второго и третьего рода. Тогда характеристическое уравнение будет иметь вид [1,2]

Ctg(n) = ^7.                          (И)

Bi

Аналогично предыдущему случаю, будем считать наименьший положительный корень этого уравнения функцией критерия Био: p = p(5z), 0 < Bi < оо . При построении графиков левой и правой частей этого уравнения в зависимости от ц,

Из графика относительной погрешности ^s/J-^fsi)

(Si)

можно увидеть, что M₂(Bi)>^₃(Bi), то есть, используя формулу (14) для определения постоянной времени, получаем одностороннее приближённое значение с избытком, но не более 5,1 %. Так же, как и в предыдущем случае, достоинство этой формулы - ее простота. Для применения запишем формулу в виде

0,4052Bz + l

^2(SO = -^:---•             (15)

Bi

становится очевидно, что

ре 0,— , 2

н(0) = 0.

функция p(Bz) возрастает. Так как в

формуле (2) постоянная времени зависит от ц2, то

Возможны ситуации, в которых 5 % будет слишком большой погрешностью и необходима более высокая точность вычислений. Для таких случаев выведем формулу с меньшей погрешностью. Аналогично предыдущей задаче воспользуемся алгоритмом Ремеза. Получим формулу

,40245/+ 0,8109)(1 + (5/+0,8051)5/

, -(°

введём функцию ц2 (^0 = И2 (^0 • Функция ц2 (^0

возрастает от 0 до —. Будем искать приближе-4

ние для ц₂ в виде (5), где три параметра А, В, С

неизвестны.

Потребуем совпадения функций p₂(Bz) и M(Bi) при Bi = ^ и Bi = оо, что даст равенства

Для вычисления значения М₂ по полученной формуле необходимо выполнить семь арифметических действий. Для того, чтобы добиться более удобного вида, запишем ее в виде суммы простейших дробей:

, а _{л АМА} 1,007    0,1179

М₂ (Bi) = 0,4024 ч----.   (16)

⁷            Bi Bz + 0,8051

Относительная погрешность полученной формулы составляет 0,8 %, что видно из графика на рис. 4.

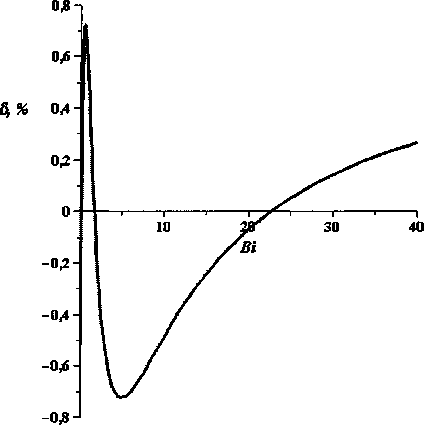
Рис. 4. Относительная погрешность формулы (16)

Коэффициенты в этом выражении определим из следующих соображений. Если р = 0, то один из критериев Bi_x или Bi₂ равен нулю, а параметр 5 совпадает со вторым из них. Имеем уже рассмотренный случай условий второго и третьего рода, и правая часть в (19) должна выглядеть как l + 45/л²                                     4

-----— (с погрешностью 5 %). Отсюда А = —, s

С = 0, D = 1. Формула (19) приобретает вид

м( ).1±±Л±±5р

V ’ s + Ep

Из свойств функции n(s,j>) следует, что

s

,2 A

л'

. о        1             и hmp2 s,— =— и ц2 s,— s^» ( 4 J Л2    (4

л2

что в применении к дроби M^s,p^ даёт равенства

Условия III рода на обеих границах

В этом случае характеристическое уравнение

ctg(n) =

ц² - Bi_xBi₂ \i^Bi_x + Bi₂) ’

1                           4       4

В/Е = \/т? и 1 + £/4 = £.Изних £=-, В = —, 3 Зя²

и окончательно

V            5 + 472/З

где В1_Х и В1₂ - критерии Био для поверхностей пластины. Обозначим s = Bi_x + Bi₂ , р = Bi_xBi₂. Считаем, что наименьший положительный корень этого уравнения есть функция параметров s,p : ц = ц^,/?) . В этих обозначениях для определения характеристического значения ц следует

Рассмотрение графика погрешности показывает, что погрешность последней формулы не более 5 %. Для применения запишем формулу в виде

, х 1 + 0,40525 + 0,135072

5 + 1,ЗЗЗр

решать уравнение 2   „ ctg(n) = ^—£.                    (18)

Ц5

Область определения функции ц^,/?): О <5 <оо, 0?<52/4. Свойства: ц(0,0) = 0,

Иш ц (5, рА = —; при р = — имеем равенство s->oo           2                4

И 5,—

~; функция ц(^,р) возрастает как

функция от р ; на граничной линии р = s² /4 име-

ем

lim ц s,—

5->00       4

= л; все линии уровня функции

p(s, р) являются прямыми. Как и раньше, для мно

жителя — в формуле (2) будем искать приближённую формулу для функции ^^s.p^—^—- в виде дробно-рациональной функции от параметров 5, р :

А/(5,72) =

1 + As + Bp C-vDs^Ep

или

, _х l + 0,4052(Bzj + £z₂) + 0,1350£z₂5z₂ М (Вй, Bi^ ) =------------------------------------.

v 1 27 Bix4-Bi2+l,333BixBi2

Более точную формулу, без заметного усложнения, авторам получить не удалось.

Сводка результатов

Сведем все возможные случаи сочетаний краевых условий и полученные формулы в таблицу.

Пример

Рассмотрим ограждающие конструкции помещений главного корпуса ЮУрГУ. Стены здания кирпичные толщиной / = 0,51 м, характеристики кирпича: плотность р = 1800 кг/м³, удельная теплоемкость с = 880 Дж/(кг*°С), коэффициент теплопроводности Х = 0,7 Вт/(м °С). Обычно расчет ведется для холодного периода, для которого коэффициенты теплоотдачи а_н =23 Вт/(м^{2 о}С), а_в =8,7 Вт/(м²*°С). Данные взяты из [4, 5]. Найдем постоянную времени.

Имеем задачу теплопроводности с краевыми условиями третьего рода с обеих сторон. Проведем необходимые вычисления. Найдем коэффициент температуропроводности а по формуле а = — = 4,41910”7 м2/с. ср

Запишем коэффициенты теплоотдачи в терминах статьи: а_х =23 Вт/(м²-°С), а₂ =8,7 Вт/(м²-°С).

Серия «Строительство и архитектура», выпуск 8

Формулы постоянной времени для неограниченной пластины

(           St    3²t _п            а/)

уравнение — = а—-, 0<я<1; Bi =—

I             9r    dr2                  X

Краевые условия		Характеристическое уравнение	Формулы для постоянной времени Т
			Точные	Приближенные (погрешность 5 %)	Уточненные (погрешность)
I и I рода	£(0,т)-1я, tQ,T^-tB '	sin(p) = 0	/2 а-л2
1иП рода	'(0,т)='я. ^^’^=0 ох	cos(p) = 0	4-/2 см^*
II и II рода		sin(p) = 0	I2
1иШ рода	^(0,т) = ^я, Ь ^0,т) = а (/я-Г(1,т))	H-ctg(p) = -Bz		/2 0,101351 + 0,3750 а В/+0.9255	/j 0,1й + 0,3365 а В/+0.8193
II и III рода	|>) = 0,	ctg(p) = n~ £>Z		/2 0,4052В/+ 1 a      Bi	/2 Гл яллл 1,007    0,1179 А — 0,4024+—---—--- а ^         Bi Bi +0,8051 J (0,8%)
III и III рода		Ctg(n) = 4Z^x ' 7 ^(b^+b^)		l2 1 + 0,4052(В/1 +В/2)+0,1350В/1В/2
				a        Bix + В/2 +1, 333BixBi2

____________________________ для определения постоянной времени

Вычислим критерии Био:

Bi, = ^ = 16,757 , Bi₂=^- = 6,339.

1 X               2 X

Найдем значение постоянной времени по соответствующей формуле из таблицы:

_ I² 1 + 0,4052 ^Bi_x + Bi₂) + 0,1 350Bi_xBi₂ _ а        Вг_х + Bi₂ +1, 333Bi_xBi₂

= 88268 с = 24,5 ч.

Затем вычислим точное значение. Для этого решим характеристическое уравнение (18), а затем подставим полученное значение в формулу (2). В результате получим точное значение постоянной времени Т =87156 с = 24,21 ч. Относительная погрешность приближенного значения 8 = 1,2 %.

Заключение

Выведенные формулы просты и удобны в применении. Они имеют небольшую погрешность, допустимую в предварительных расчетах. Их можно использовать для получения начальных приближений в численных методах. Похожим образом можно получить подобные формулы для других случаев (цилиндра, шара).