Ионная ловушка с суперпозицией линейных высокочастотных и однородных статических электрических полей

Ионные ловушки, в которых реализуется механизм удержания заряженных частиц в статических или динамических электрических и магнитных полях, являются эффективным инструментом масс-сепарации и транспортировки заряженных частиц [1–3]. Ионные ловушки со статическими электрическими полями (ловушка Кингдона) [4–7] и скрещенными статическими электрическими и магнитными полями (ловушка Пеннинга) [8–9] используются в качестве измерительных ячеек в масс-спектрометрах (МС) высокого разрешения с преобразованием Фурье. В [10] разработан общий подход к синтезу электростатических ионных ловушек для пространственной фокусировки и времяпролетного масс-разделения заряженных частиц. Радиочастотные ионные ловушки в МС с разрешением до нескольких тысяч выполняют функции масс-анализаторов, ячеек фрагментации и транспортировки заряженных частиц [1, 2]. Использование радиочастотных ионных ловушек в качестве измерительных ячеек МС с преобразованием Фурье ограничено сложностями выделения наведенных токов малого уровня на фоне интенсивных наводок от ВЧ-полей анализаторов [11]. Ослабление уровня ВЧ-наводок на детектирующих электродах на 3–4 порядка при сохранении высокой линейности квадрупольных полей позволит рассматривать радиочастотные ионные ловушки как альтернативу статическим ловушкам для их использования в качестве измерительных ячеек в МС с преобразованием Фурье. Такая задача может быть решена с помощью ионно-оптических систем (ИОС) с плоскими дискретными электродами, позволяющими образовывать суперпозиции электрических полей с различными пространственно-временными распределениями потенциала [12–16].

ДВИЖЕНИЕ ИОНОВ В СУПЕРПОЗИЦИИ ЛИНЕЙНЫХ ВЧ И ОДНОРОДНЫХ СТАТИЧЕСКИХ ПОЛЕЙ

Рассмотрим ИОС с двумя плоскими дискретными электродами (рис. 1). К i -м элементам дискретных электродов 1 и 2, где i = ± ( 0, 1, 2, . „ , n ) , приложены комбинации постоянных и переменных напряжений

U „ ( t ) = U 0 - u ( t ) , U 2 ( t ) = -U 0 + u ( t ) ,     (1)

где u, ( t ) = A V • i • cos ( tot + ф ) , A V = V / n , V , to , φ — амплитуда, частота и фаза ВЧ-напряжений. При этом в рабочей области ИОС I x | <  x a , Ь| <  У a , где x _a и y _a — параметры ИОС, образуется суперпозиция двумерного линейного ВЧ и однородного статического полей с распределением потенциала

,     . 2 V • cos (tot + ф) X ф (x,y,t) =--------2------xy + U0—,      (2)

r02                   xa где r0 = 2xa ya — геометрический параметр ИОС. Движение ионов в плоскости XOY в этом случае описывается системой уравнений лярные составляющие колебаний ионов, линейное ВЧ электрическое поле заменим эквивалентным статическим полем с распределением псевдопотенциала

U 1 i ( t )

U 2 i ( t )

Ф п ( ^Х,У ) Л ( x^{2 +}У ²) , r ₀

где псевдопотенциал линейного ВЧ электрического поля расчитывается по формуле [1, 2]

X

m =q m r02ω2 m    4

В этом случае суперпозицию двумерного линейного ВЧ и однородного статического электрических полей можно рассматривать как статическое поле с распределением потенциала

Ф с ( ^Х,У ) = U r ( x^{2 +}У ²) ^{+ U} о x .         ⁽⁷⁾

r ₀²                    x _a

Движение ионов по осям X и Y в статическом поле с распределением потенциала (7) описывается уравнениями

Рис. 1. Ионно-оптическая система с плоскими дискретными электродами 1 и 2 (пунктирные линии) для образования суперпозиции линейного ВЧ (сплошные линии) и однородного статического (точечные линии) электрических полей

d² x 2 eU _п     e U ₀

"71---2— x +---0, dt2   r2m    m x

0a

d 2 y d t ²

—

2 eU п r 0 ² m

y= 0.

d2 x dtг d2 У . dt2

— 2 q [ cos ( ro t + ф ) ] y + p x = 0,

- 2 q [ cos ( ro t + ф ) ] x = 0,

где q = 4 eV / r ₀ ² ω ² m , p_x = eU ₀ / mx _a, m и e — масса и заряд ионов. При p_x = 0 и q « 1 решения системы уравнений (3) с некоторыми приближениями можно представить в виде гармонических функций [14]:

x ( t ) = x ₀ cos ( Qt ) ⁺ “ °^ sin ( Qt ) , y ( t ) = y o Cos ( Qt ) + Q sin ( Qt ) ,

где x ₀ , y ₀ , v _{0 x} , v _{0 y} — начальные координаты и скорости ионов, Ω = 2 eV / r ₀ ² ωm — секулярная частота. В этом случае траектории движения ионов в плоскости XOY будут близки к эллипсам с центрами в начале координат.

Для нахождения приближенных решений уравнений (3) при p_x = 0 , учитывающих только секу-

Решения уравнений (8) имеют вид x (t) =( x0 — xc) cos (Qt) +—sin (Qt) + x c, Ω                (9)

v ₀

y (t) = y 0cos (Qt) + ^y sin (Qt), где xc = r02U0 / xaUп . Выражения (9) являются уравнениями эллипсов в параметрическом виде с координатами центров ( xc , 0). Из сравнения (9) и (4) следует, что действие однородного статического поля на движение ионов в суперпозиции с линейным ВЧ-полем состоит в смещении центров эллиптических траекторий в направлении действия статического поля. Величина сдвига xc зависит от параметров статического и ВЧ полей и массы ионов r4ω2U x = 0     0 m .

^c 2 ex V ²

a m

Точные решения уравнений (3), кроме составляющих с секулярной частотой Ω , содержат ВЧ-гармоники с частотами ω = kΩ , где k = 1,2,3 ,… [14].

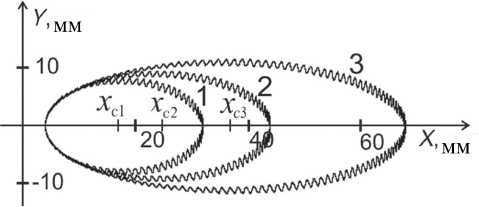
Рис. 2. Траектории движения ионов в суперпозиции линейного ВЧ и однородного статического электрических полей с параметрами r ₀ = 60 мм, V = 1 кВ, f = = 1 МГц, U 0 = 6 В.

1, 2, 3 — m = 60, 91, 136 а.е.м.

Так как амплитуды ВЧ-гармоник пропорциональны q^k / 4 ^{( 2 k} - 1 ) , точность выражений (9) возрастает с уменьшением параметра q . При q <  0.1 амплитуды высших гармоник не превышают уровня 0.025 амплитуды секулярной гармоники. Результаты компьютерного моделирования траекторий движения ионов в суперпозиции линейного ВЧ и однородного статического электрических полей приведены на рис. 2.

Выражения (9) можно представить в виде x ( t ) = Xm cos ( ^+Фх ) + xc,

У ( t ) = ^Y m C^0S ( ^t + Ф у ) ,

где

X m = V ( x 0 - x c ) ^{2 +} ( v 0 x / ^Q ) ^{2 ,} Ym^ 2 + ( v 0 у / ^Q ) ² , Ф х = arctg [ ( x 0 - x c ) ^Q / v 0 x ] , Ф у = ^arc tg [ У 0 ^Q / ^V 0 y ] — амплитуды и фазы секулярных колебаний ионов по осям X и Y . Из (11) следует, что изменением параметра U ₀ / x _a статического поля можно изменять положение x _c и амплитуду X_m периодических колебаний ионов на плоскости XOY при неизменной их частоте Ω . Это свойство колебаний ионов в суперпозиции линейных ВЧ и однородных электрических полей можно использовать для разработки новых методов энерго- и масс-сепарации, транспортировки и фокусировки заряженных частиц.

Для практического использования представляют интерес ионные ловушки с близкими к гармоническим колебаниями ионов в полупространстве x> 0 . Из (11) следует, что режим монополярных по оси X колебаний ионов в суперпозиции линейного ВЧ и однородного статического электрических полей реализуется в случае x0

x. c 22

После подстановки в (12) выражений для xc и Ω получаем условие монополярности колебаний qV x022

U0 >      2 +,

8 r02

где W _{0 x} — начальная энергия ионов в направлении оси X .

МОНОПОЛЯРНАЯ ИОННАЯ

ЛОВУШКА-MONOTRAP С СУПЕРПОЗИЦИЕЙ ЛИНЕЙНОГО ВЧ И ОДНОРОДНОГО СТАТИЧЕСКОГО ЭЛЕКТРИЧЕСКИХ ПОЛЕЙ

Режим монополярных по оси X колебаний реализуется в ИОС, изображенной на рис. 3.

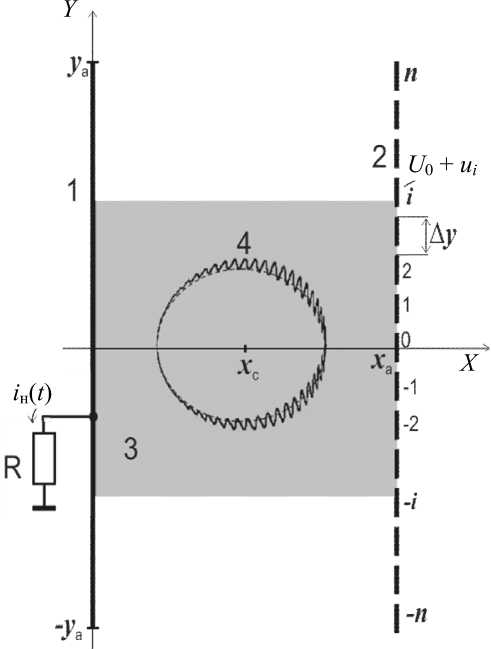
Рис. 3. Ионно – оптическая система с суперпозицией линейного ВЧ и однородного по оси X статического электрических полей с периодическими в полупространстве x > 0 колебаниями ионов.

1 — сплошной заземленный по ВЧ электрод; 2 — дискретный электрод; 3 — рабочая область анализатора

Система состоит из двух в плоскостях x = 0 и x = x _a электродов: 1 — сплошного и 2 — дискретного с размерами по осям Y и Z 2 у a , 2 z a » x a . Электрод 1 заземлен, а к дискретным элементам электрода 2 приложены постоянное U 0 и переменные ui = ЛК ■ i ■ cos ( rot ) напряжения. При шаге дискретизации А у <  0.1 у _a относительные отклонения распределений ВЧ и статического потенциалов от идеального (2) в рабочей области 0 <  x <  x a - А у , |у | <  у a - x a не превышают уровня 10 ^{- 4} .

Используя условие монополярности колебаний (13) для границ диапазона масс ионов, удерживаемых по осям X и Y в ИОС на рис. 3, получаем x2eV 2 W mmax = 4a 2 , mmin = 0x mmax. (14) r04ω2U0 eU0

Выбором геометрических и электрических параметров ИОС диапазон удерживаемых масс может устанавливаться в пределах m max / m min = 2 ^ 10 и изменением параметров V и ω ВЧ-напряжения перестраиваться в широких пределах.

В ИОС на рис. 3 поле вдоль оси Z отсутствует, и движение ионов в этом направлении определяется их начальными энергиями W _{0 z} . Если ИОС дополнить двумя электродами в плоскости z = 0 и z = z _a с задерживающим потенциалом Uz > W ₀ z [ eV ] , колебания ионов с массами m _max > m > m _min будут ограниченными по всем координатам: 0 <  x <  x a , | у | < у a , 0 < z < z _a. По оси X координаты ионов всегда положительные, поэтому ИОС с комбинацией линейного ВЧ и однородного статического электрических полей в полупространстве x >  0 можно рассматривать как монополярную ионную ловушку — monotrap. Комбинирование ВЧ и статических электрических полей в monotrap может быть использовано как для усовершенствования аналитических и коммерческих характеристик , так и разработки новых, более эффективных систем масс-разделения, удержания и транспортировки ионов.

Рассмотрим возможность использования monotrap в качестве измерительной ячейки МС с преобразованием Фурье. Конструкция ИОС monotrap позволяет оптимальным образом совместить процессы детектирования наведенных токов и подавления наводок от ВЧ-полей анализатора. Так как колебания ионов по оси X с секулярными частотами Ω происходят между параллельными электродами ИОС monotrap, наведeнные на них токи будут изменяться по гармоническому закону

ⁱ н ( t ) = Im • sin ( ^t ) ,             ⁽¹⁵⁾

где I_m = NeΩX _m x _a , N — число ионов. Гармонический характер изменения во времени наведенных токов на электродах monotrap является условием отсутствия комбинационных составляющих в получаемых с помощью преобразования Фурье масс-спектрах. Высшие гармоники колебаний ионов с частотами | к ±^в | ro » Q и малыми при

V 2 7

в « 1 амплитудами X_mk « X_m практически не

ограничивают диапазон масс измеряемых спектров.

Другое полезное свойство monotrap состоит в возможности подавления при детектировании наведeнных токов фона от ВЧ-поля, т. к. две симметричные половины дискретного электрода 2 с противофазными ВЧ-потенциалами ui = - u - i создают на детектирующем электроде 1 две одинаковые по величине, но противоположные по знаку ВЧ-наводки. Симметрированием электродной системы monotrap и еe ВЧ-питания, а также использованием режекторных фильтров можно добиться высокой степени подавления фонового ВЧ-сиг-нала.

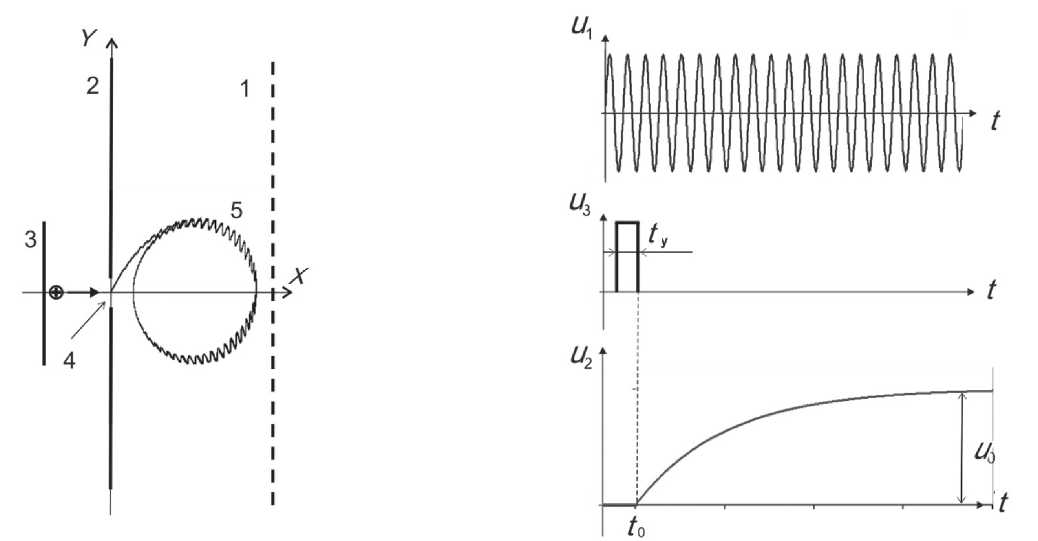
Monotrap также позволяет эффективно организовать процессы ввода и захвата анализируемых ионов. ИОС и временные диаграммы на электродах monotrap во время ввода и захвата ионов показаны на рис. 4. Ввод ионов осуществляется через щель 4 в детектирующем электроде 2. Анализируемые ионы могут быть образованы между детектирующими 2 и ускоряющим 3 электродами или введены в пространство между ними с помощью системы транспортировки от внешнего источника. Под действием импульсного напряжения u ₃ ионы ускоряются в направлении оси X и через щель 4 в электроде 2 поступают в рабочую область monotrap. Для перевода ионов с начальными параметрами x ₀ = 0 , v _{0 x} >  0 в режим периодических по осям X и Y колебаний напряжение на электроде во время ввода изменяется по экспоненциальному закону

u ₂ = U ₀

1 - e (t t0)/т

При использовании псевдопотенциальной модели ВЧ квадрупольного поля движение ионов с момента ввода t ₀ описывается уравнением

d 2 x d t ²

- e

m

2 U п r 0 ²

U x + ⁰

(    -t ^

1 - e^

x a V

б

а

Рис. 4. Схема ИОС (а) и временные диаграммы во время ввода и захвата ионов (б) в monotrap.

1, 2, 3 — дискретный, сплошной и ускоряющий электроды с напряжениями u 1 , u 2 , u 3 ; 4 — щель для ввода ионов; 5 — траектория ионов

решение которого имеет вид x (t) = x / x f vn     x Qt i \

---c— cos ( Qt ) + 0^-- ^c—— Sin ( Qt ) + (18) 1 + Q²т^{2 V} И Q 1 + Q²т ² J ^{V (18)}

+ x _c

fl     Q ² т ²    - t )

1    - ,        2 eT

1 + Q T

Параметры τ и U ₀ экспоненциального напряжения определяют граничные значения параметра Матье q _max , q _min и соответственно границы массового диапазона m _min , m _max анализатора. По результатам численного моделирования для практически реализуемых параметров monotrap установлено, что минимальная граница параметра Матье определяется соотношением q _min = 10 / τω , а диапазон его изменения составляет q / q = 5 ^ 6. max min

Таким образом, изменением параметров τ , U ₀ однородного поля и V , ω квадрупольного поля диапазон масс monotrap может изменяться в широких пределах.

ЗАКЛЮЧЕНИЕ

Рассмотренные свойства ионной ловушки с суперпозицией линейных радиочастотных и однородных статических электрических полей в сочетании с новой технологией образования таких полей системами плоских дискретных электродов позволяют использовать monotrap в качестве анализатора в масс-спектрометрах с преобразованием Фурье.