Исчерпание мест зарождения и кинетические параметры аустенитферритного превращения в сплавах Fe - 9 % Cr

Зарождение при фазовых превращениях в твёрдом состоянии часто происходит на границах зёрен. В классической работе [1] Дж. Кан подробно рассмотрел кинетику фазового превращения в условиях, когда зарождение новой фазы происходит на гранях, рёбрах или в вершинах зёрен, получил общие уравнения, описывающие изменение доли образующейся фазы со временем, и определил условия предпочтительной реализации тех или иных мест зарождения. Эти результаты подробно описаны также в монографии Дж. Кристиана [2]. Во всех случаях теория Кана предсказывает явление, которое он назвал исчерпанием (saturation) мест зарождения: доля оставшихся непревращён-ными границ (граней, рёбер, вершин) зёрен со временем убывает быстрее, чем доля непревра-щённого объёма, и процесс зарождения практически прекращается ещё до того, как превращение завершится; после этого оно развивается лишь за счёт роста уже существующих частиц новой фазы.

Кинетика изотермического фазового превращения обычно описывается уравнением Аврами fv = 1 - exp (-Ktn), (1) где fV – доля превращённого объёма; t – время; K и n – коэффициенты. Для определения этих ко- эффициентов экспериментальную кривую f (t) перестраивают в двойных логарифмических координатах In (- ln(1 - fv)) - In t, в которых уравнение (1) превращается в уравнение прямой с наклоном n:

In ( - ln(1 - f_v ) ) = n In t + In K . (2) Если скорости зарождения и роста частиц постоянны, то исчерпание мест зарождения по Дж. Кану проявляется в постепенном уменьшении наклона кривой превращения в этих координатах от n = 4 до n = 1, 2 или 3 соответственно для зарождения на гранях, рёбрах или в вершинах зёрен.

Типичный пример такого поведения наблюдался в работах [3, 4] для у^а-превращения в сплавах Fe–9 % Cr. Так, для сплава, содержавшего 0,04 % C, кинетические кривые в двойных логарифмических координатах обнаруживали отчётливый излом со сменой наклона от n = 3,5... 4,0 до n = 1,0...1,1 (рис. 1). В микроструктуре уже на ранних стадиях отчётливо наблюдалось формирование сетки из плоских кристаллов феррита вдоль границ аустенитных зёрен, от которой в дальнейшем происходил рост вглубь зёрен с сохранением плоской формы фронта или в виде видманштетто- вых пластин [4]. Момент, когда по микроструктурным наблюдениям завершалось формирование сетки, соответствовал моменту смены наклона кривых ln ( -ln(1 -fV ) ) – ln t при соответствующей температуре [4].

f_S = 1 - exp

-J Isd т-п«2 (t -т)2 I 0

, I ^п T 2,3

1 - exp I - —IS « x t

где произведение I_Sd τ отражает число частиц,

-5 0

-1

-2

-3

-4

46 ln t [с]

зародившихся в промежуток времени от τ до τ+ d τ , а πω 2 _x ( t - τ ) 2 – площадь, занимаемую каж-

дой из этих частиц к моменту t .

Введём, следуя [1], безразмерный параметр

DS

η=

V

где D , S и V – средний поперечник, пло-

щадь поверхности и объём зерна; для шара и куба η = 6 , для кубооктаэдра Кельвина η= 6,70 . Далее будем считать, что от тех участков границы, которые претерпели превращение, начинается рост вглубь зерна (по нормали к границе) со скоростью ω _z . Прирост превращённой площади граней в

единице объёма за промежуток т...т + d т равен

Рис. 1. Кинетические кривые превращения аустенит → феррит в сплаве Fe – 9,24 % Cr – 0,04 % C, перестроенные в двойном логарифмическом масштабе [3, 4]

^η df = D^S

η df_S Ddt

dτ= t=τ

Внешне эти результаты точно соответствуют теории Кана. Однако в работе [1] он в действительности рассматривал несколько иную ситуацию, считая, что зародившиеся на границах частицы новой фазы растут с одинаковой скоростью во всех направлениях, сохраняя до момента столкновения друг с другом сферическую форму.

Поэтому проведём повторное рассмотрение кинетики превращения в условиях исчерпания мест зарождения, основываясь на экспериментально наблюдавшихся в [4] особенностях морфологии роста частиц. Будем считать, что зарождение частиц новой фазы происходит на гранях зёрен, после чего они начинают расти в плоскости грани в двух направлениях с постоянными скоростями ω _x =ω _y (рис. 2). Если число зародышей, образующихся на единице площади грани зерна в единицу времени I S также постоянно, то согласно уравнению А.Н. Колмогорова [2], доля площади границы, где превращение уже прошло, будет увеличиваться со временем по закону

П Г 2 2 I П 23|>

- D nIS «2т2 exp I - 3 IS «2T3 I dт,

и к моменту t фронт превращения успеет пройти от этих участков вглубь зерна расстояние ω _z ( t -τ ). Тогда доля превращённого объёма

f_V = 1 - exp

1 - exp

I T=t                       ^

- J D ^df S •« z ⁽ t ^{-T )}

{-es [ast (1- exp (-ast3

I 4 зз

^-YI 3, ^a s t

I П | где aS = I 3 IS «x I ,

-

β _S = ^{η ω z} , а γ ( a , x ) = D α S

x

= J e ^- y y a ^{- 1} dy - неполная гамма-функция [5].

Имеются работы, показывающие, что зарождение феррита происходит не равномерно по всей площади границ аустенитных зёрен, а преимущественно в их вершинах [6]. В таком случае во всех

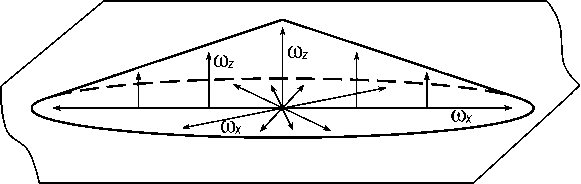
Рис. 2. Модель частицы, зарождающейся на границе и растущей в плоскости границы и вглубь зерна с различными скоростями

приведённых выше выражениях следует заменить

скорость зарождения I S на I

N N_S ^,

где I N N – число

, _I 4 _ 3 ,3 I 3 _ 4 ,4 r<-i                                 z^x

YI 3, a _st I« 4 a _st [5], поэтому вместо (5) получим

зародышей, образующихся во всех N вершинах зерна за единицу времени; при этом для идеальной полиэдрической структуры среднее значение N ≈ 22,79 [7]. Средний плоский угол у вершины грани ϑ ≈ 1,911 рад [7], а поскольку зародившаяся частица начнёт расти со скоростью ωx в плоскостях трёх сходящихся в вершине граней и со скоростью ωz вглубь зерна, то ωx, в свою очередь, ϑ следует заменить на 3ωx ≈0,912ωx . Коэффи-2π

f_V ≈ 1 - exp

- 4 β _S α 4 _S t 4

, I П n Г 2    ,4

= 1 - exp - I ω ² ω t ⁴

I 12 D S x ^z

.

(6а)

Напротив, при t >>  1 α _S имеем exp( -α 3 _S t 3 ) ≈ 0 и

γ ( 4 3, α 3 _St 3 ) ≈ Γ ( 4 3 ) ≈ 0,8930 , поэтому

f_V ≈ 1 - exp ( -β _S α _St ) = 1 - exp

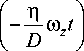
(6б)

циент α _S в уравнении (5) будет тогда иметь вид

αS=

3 ϑ ² N 1 4 π S

I/з

I N ® X I

19,87 I ω ² η Nx

Заметим, что выражение (5) отличается от того, которое получается в теории Кана [1] потому, что в нашей модели форма продолженного объёма каждой частицы новой фазы представляет собой не шар с радиусом ω ( t -τ ), а конус с радиусом ос-

Таким образом, график функции (5) в двойных логарифмических координатах должен плавно менять свой наклон от 4 до 1, как и в теории Кана, а выражения (6а) и (6б) являются его асимптотами (рис. 3). Можно считать, что выражение (5) аналогично уравнению Аврами (1), но с переменными коэффициентами n и K , причём текущее значение

нования ω _x ( t -τ ) и высотой ω _z ( t -τ ) (см. рис. 2). Кан находил продолженный объём каждой частицы путём интегрирования от нуля до ω ( t -τ ) величины S_z dz , где S z – площадь сечения частицы плоскостью, проведённой параллельно границе на расстоянии z от неё. Однако даже при одинаковых скоростях роста ω=ω _x =ω _y =ω _z для сферической частицы S z =n [to ²( t -t ) ² - z ² J , а для конической S_z =π [ ω ( t -τ ) - z ] 2 . Расчёт f V по методу [1] с использованием второго выражения даёт результат, совпадающий с (5).

При малых временах ( t <<  1 α _S ) можно использовать разложения exp( -α ³ _S t ³) ≈ 1 -α ³ _St ³ и

n равно dln(-ln(1-fV)) n== dlnt

= 1        y ( 4/3, « S t ³)    '

a S t ( 1 - exp( -a S t ³) )

График функции показан на рис. 4 в сравнении с аналогичной зависимостью согласно теории Кана [1].

Исчерпание зарождения происходит в момент, когда доля превращённых границ зёрен f S становится достаточно большой. Из (3) и (5) можно найти связь долей превращения на границе и в объёме:

f_V = 1 - exp

- 3 e s [ф s (1- exP(-vS))

-

I 4 з

-YI 3,Фs

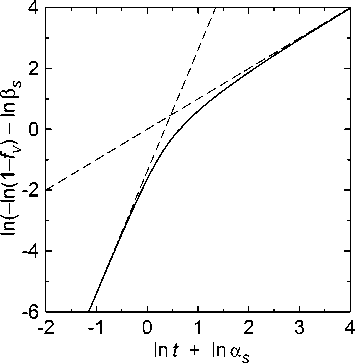
Рис. 3. График функции (5) в двойном логарифмиче-

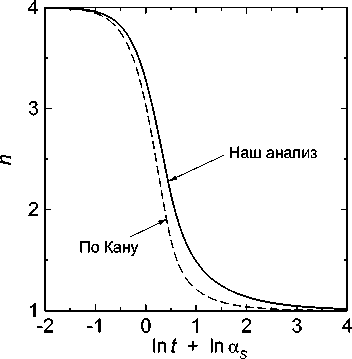
Рис. 4. Зависимость показателя n от времени согласно нашему анализу [формула (7)] и по Дж. Кану [1]

ском масштабе

где ϕ _S = ( - ln(1 - f_S ) ) ¹³. Удобно принять, что мо-

мент исчерпания зарождения соответствует излому экспериментального графика ln ( - ln(1 - f_V ) ) – ln t (как на рис. 1) или точке пересечения асимптот. Приравнивая (6а) и (6б), найдём положение этой точки:

ln t = 3ln4 - ln α _S ≈ 0,4621 - ln α _S ;

(9а)

1 ln( - ln(1 - f_V ^*)) = ₃ln4 + ln β _S ≈

≈ 0,4621 + ln β _S .                           (9б)

Сопоставляя (8) и (9б), найдём, что точке излома соответствует ϕ ^* _S ≈ 2, 4804 и f_S ^* ≈ 1 - 2,4 ⋅ 10 ^{- 7}. Величина же объёмной доли превращения в этот момент определяется β S – соотношением скоростей развития превращения на границе и в объёме согласно (9б).

Выражения (9) позволяют найти коэффициенты α S и β S , если известны точки излома кинетических кривых в двойных логарифмических координатах (как на рис. 1). Как было показано в [3], общая энергия активации превращения на ранних и поздних стадиях, когда зарождение происходит и когда оно практически прекратилось, не зависит от температуры, что, по-видимому, свидетельствует о малости работы образования критического зародыша. В таком случае температурные зависимости скоростей зарождения и роста практически совпадают. Поэтому, следуя [3], можно записать

α - фаз соответственно при данной температуре T и при температуре T_s, являющейся верхней асимпто той С - образной кривой ( которая несколько смеще на относительно равновесной температуры T 0 , где Δ G = 0 ; слагаемое Δ G s отражает затраты свобод ной энергии на формирование межфазной поверх ности , а также упругих напряжений и дислокаций в α - фазе [8]); как и в [3], мы далее будем рассчи тывать Δ G и Δ G s по данным работ [9, 10]. Для ско рости роста в объём зерна ω z значения энергии активации U₂ и константы C₂ могут иметь иные

значения , чем для процессов зарождения и роста на границе , поэтому коэффициент

β =ηωz DαS

AG-AG   I U, ) 1

= C ^s exp - ²

^x RT V RT J a S

C I = TrexpI -

C i      v

U2

- U ₁

RT

.

(10 б )

I П г 2 а 5 = I 3 IS ^x

= C 1

Δ G - Δ G_s RT

(10 а )

где R – газовая постоянная ; U 1 – энергия актива ции ; C 1 – константа . Величины Δ G и Δ G s пред ставляют собой разности свободных энергий γ - и

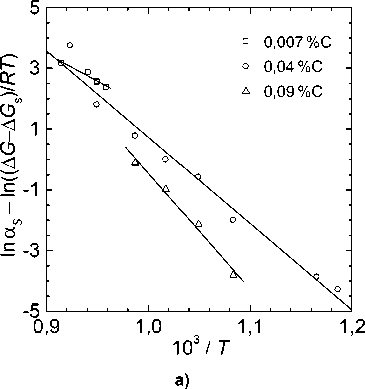
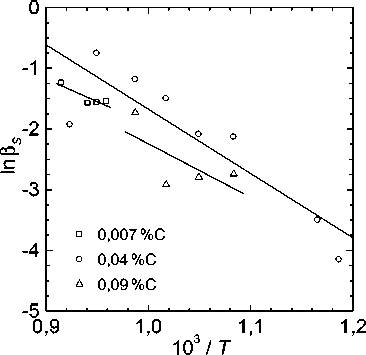
Рис. 5. Определение кинетических параметров превращения по моментам исчерпания мест зарождения (на основе экспериментальных данных [3])

Логарифмируя (10а) и (10б), получаем Δ G -Δ G       U 1

ln α- ln         s = ln C - 1 ;

^S RT ¹ R T

(11 а )

ln β S = ( ln C 2 - ln C 1 ) - ^{U 2 - U 1 1} .        (11б)

RT

Следовательно, если найти точки излома на графиках экспериментальных зависимостей ln ( - ln(1 - f_V ) )

от ln t , определить по формулам (9) значения α S и

β S , а затем отложить

ln α _S

Δ G -Δ G

- ln ^s

RT

и ln β _S

как функции обратной температуры, то мы должны получить прямые, коэффициенты уравнений которых позволят найти величины как энергий активации U 1 , U 2 , так и констант C 1 , C 2 .

Такие графики для трёх сплавов Fe–9%Cr с 0,007; 0,04 и 0,09 % C, изученных в работе [3], приведены на рис. 5, а найденные значения параметров – в таблице. Обратим внимание, что U 1 = (0,7…0,8) U 2 . Соотношение энергий активации зернограничной и объёмной диффузии Q _гз и Q _об

б)

Кинетические параметры аустенит-ферритного превращения в сплавах Fe–9 %Cr

C, мас. % Cr, мас. % т s, °C ln C1, [c–1] lnC2, [c–1] U1, кДж/моль U2, кДж/моль U0,05, кДж/моль [3] U0,50, кДж/моль [3] 0,007 9,24 835 19,7 25,3 150 213 212 231 0,04 9,24 815 29,2 38,1 237 325 290 315 0,09 9,38 800 37,8 44,4 318 391 349 341 близко к этому и обычно составляет 0,4–0,6. В частности, для самодиффузии в у-железе Qгз =160, а Qоб =284 кДж/моль [11], то есть Qгз = 0,56·Qоб; для диффузии хрома в у-железе Qгз = 209 или 238, а Qоб =409 кДж/моль [12], то есть Qгз =(0,51…0,58)Qоб.

Значения U ₁ и U ₂ увеличиваются с ростом содержания углерода. Если значения для сплавов с 0,007 и 0,04 % C сопоставимы с энергией активации самодиффузии в железе, то при 0,09 % C они приближаются к энергии активации диффузии хрома.

В той же таблице для сравнения приведены значения энергий активации U 0,05 и U 0,50 , определённые в [3] по температурной зависимости времени достижения степеней распада f V =0,05 и 0,50. Видно, что полученные из нашего анализа значения энергии активации U ₂ очень близки к U _0,50: так как при f_V = 0,50 практически идёт только рост феррита от границ к центру аустенитных зёрен со скоростью to z . В то же время U 1 заметно меньше, чем U _0,05; поскольку до исчерпания мест зарождения превращение развивается как за счёт зарождения и роста на границах, так и за счёт роста в объём зерна, то общая энергия активации превращения должна иметь значение, промежуточное между U 1 и U 2 .

Найденные значения параметров позволяют рассчитать полную диаграмму изотермического распада аустенита: либо по точной формуле (5), либо приближённо на основе формул (6а) и (6б):

I 1 1

1 - exp —Рс.а 4 t ⁴ при t <  4 1 ³ а,¹;

^РI ⁴ S S J ^Р S (12а)

• 1    - exp ( -Р S а S t ) при t >  4¹³ а -¹

или t = ‘

(-l-d - fv) )^ a S PS при fv 51 - exp (-4V3Ps );

(-ln(1 - fv)) -^7" a S P S при fv >1 - exp (-4V3 pS).

(12б)

Такая диаграмма для сплава с 0,04 % C при значениях параметров из таблицы приведена на рис. 6. Видно, что она хорошо совпадает с экспериментальной во всём диапазоне температур и долей превращения.

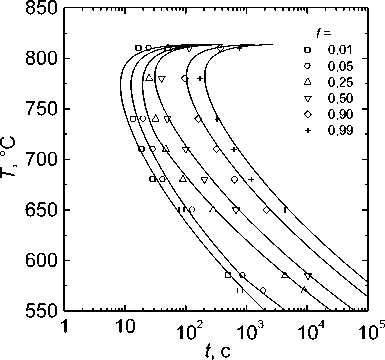
Рис. 6. Сравнение экспериментальной [3] диаграммы превращения аустенит ^ феррит в сплаве Fe–9,24%Cr–0,04%C с рассчитанной по формуле (12б)

Таким образом, разработанная теория не только лучше соответствует наблюдавшимся микроструктурным особенностям аустенит-ферритного превращения в сплавах Fe–9%Cr, но и позволяет раздельно определить кинетические параметры зарождения и роста на границе и в объёме зерна и даёт возможность при помощи единой формулы описать полную диаграмму распада аустенита в условиях исчерпания мест зарождения на границах зёрен исходной фазы.

Работа выполнена в рамках ФЦП «Научные и научно-педагогические кадры инновационной России».