Искусственный нейрон на синхронной логической свертке

Искусственный нейрон – это элемент, выполняющий простейшее преобразование комбинации входных сигналов с определенными весами, определяющими связь. Выходным сигналом является активационная функция, от полученной комбинации входных сигналов. Математическое описание нейрона можно представить в виде:

Реализация нейронных сетей, построенных на основании подобных элементов, является основной проблемой, связанной с усложнением процедур обработки информации и повышением требований к быстродействию и эффективности, и делает актуальными вопросы проведения быстрого анализа и синтеза систем информационной об- работки сигналов, создания новых алгоритмов, разработки методологии системного подхода к решению информационных задач. Обработка сигналов в дискретном времени применима к широкому классу сигналов и систем, поэтому создание новых концепций и разработка новых приложений также актуальны.

Если в основе технологии программирования использовать логические принципы анализа и синтеза дискретной обработки, в частности, использование унитарного сигнала, где обработка информации будет производиться на начальном этапе приема, передачи и обработки информации, то это позволит увеличить скорость и объем передаваемой информации, эффективность использования аппаратных средств по сравнению с аналогичными методами при использовании цифровой обработки сигналов.

Логические операции с PZ-рядами

Синхронный унитарный сигнал (СУС) – синхронная последовательность единиц, в которой информационная величина представляется в виде Р-ряда (P-prima) или Z-ряда (Z-zero). Информационным параметром является длина ( N_Р ) Р-ряда и длина ( N_z ) Z-ряда.

На дискретной шкале СУС может быть представлен в алгебраической или логической форме, например:

А(p)= Pk + Pm, или А(p) = Pk ٧ Pm, где k, m – показатель степени, определяющий местоположение переменной P в ряду.

Для компактности удобно пользоваться векторной формой записи многочленов, например:

А(p) = А(k,m) = Pк+ Pк+1+ Pк+2+

+ ...+Pm, где k – начало, m – конец ряда, « , »– символ итерации (продолжения) ряда.

В результате такого представления преобразование сигналов может быть сведено к преобразованию PZ-рядов, и формализовать логическую обработку сигналов.

Логические схемы в сочетании с синхронными элементами задержки позволят выполнять различные операции с унитарными рядами: расширение, ограничения, выделение фронтов, удвоение, селекцию по длине ряда, выборку комбинаций по шаблону, проверку условий, умножение и деление на фиксированный многочлен, преобразование, кодирование и декодирование комбинационных рядов.

При описании синхронных величин удобно использовать запись комбинаций в виде многочлена с фиктивной переменной. Индекс фиктивной переменной показывает местоположение переменной в разрядной сетке логического слова или величину задержки.

Синхронную логическую функцию, определяющую соответствие между логическими выражениями исходных двоичных последовательностей и задержанных по очереди, будем называть синхронной логической сверткой [1]. Для формализации анализа и синтеза синхронных унитарных устройств введен оператор логической свертки:

C(pn+m) = A(pn) Θ В(pn+1), где A(p) =a0P0 + a1P1 + a2P2+ … – входная последовательность, ai = {0,1}– переменная, которая определяет наличие или отсутствие переменной pi в многочлене А(p), В(p)=A(p)·p – многочлен задержки входной последовательности, Θ – символ логической операции из множества W[∧, ∨, ⊕, ▷, ◁], где ∧ – конъюнкция, ∨ – дизъюнкция, ⊕ – сложение по модулю два, ▷ – прямой запрет, ◁ – обратный запрет.

Из всего многообразия операторов логической свертки выделен функционально полный набор из пяти операторов:

Сδ(p) = A(p) ∨ B(p) → СДС, Ck(p) = A(p) ∧ B(p) → СКС, Cϕ(p) = A(p) ∧ B(p) → СФС,       (2)

Cs(p) = A(p) ∧ B(p) → ССС, Cµ(p) = A(p) ⊕ B(p) → СМС.

Синхронная дизъюнктивная свертка (СДС) – увеличивает количество единичных интервалов СУС на величину К Д (количество последовательно включенных элементов СДС).

Синхронная конъюнктивная свертка (СКС) – уменьшает количество единичных интервалов СУС на величину К_К (количество последовательно включенных элементов СКС).

Синхронная свертка по модулю два (СМС) – выделяет стробы, совпадающие с первыми интервалами F_P и F_Z единичных и нулевых последовательностей, то есть отмечает (маркирует) все перепады значений входной последовательности.

Синхронная конъюнктивная свертка с инверсией задержанной входной переменной (СФС) – формирует импульс F_p , совпадающий с первым интервалом последовательности единиц.

Синхронная конъюнктивная свертка с инверсной входной переменной (ССС) выделяет строб F_Z и идентифицирует скачок последовательности нулей.

При ограничениях по количеству входов целесообразно создать программируемый модуль, позволяющий реализовать функционально полный набор логических сверток.

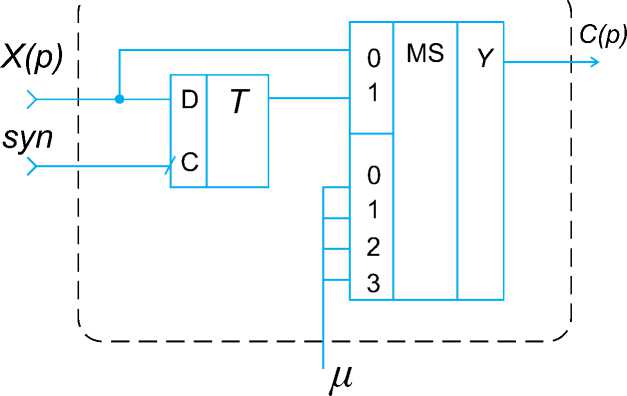
Рис. 1. Весовой элемент на управляемом модуле операторами логической свертки

Управляемый модуль ( рис. 1 ), реализующий функционально полный набор операторов свертки (2), синтезирован при помощи мультиплексора селекто-ра[4].

Модель нейрона на логической свертке

При разработке функциональных устройств на операторах логической свертки [1 – 4] с их реализацией на программируемых логических интегральных схемах возникает возможность реализации отдельных составляющих математического нейрона на элементах пороговой логики, что позволяет представить их как новый класс устройств, оперирующих в пространстве синхронных унитарных сигналов, и выполняющих преобразования над ними по аналогии с математической моделью. Дальнейшее обозначение сигналов будет базироваться в соответствии с устоявшейся терминологией нейронных сетей.

Весовая составляющая связи нейрона преобразует сигнал для суммирования на элементах, реализация которых является не столь сложной, в отличие от блоков умножения, заложенных в весовой концепции преобразования. Сложность увеличивается с переходом от пороговой логики преобразования сигнала к умножению с рациональными числами.

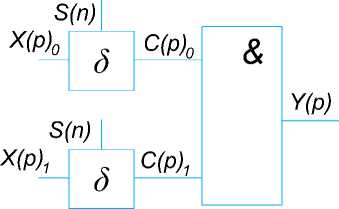
Рис. 2. Конъюнктивный пороговый элемент с δ – весовыми элементами Процедура преобразования:

Y(p) ^ {(X(P) o ° 5 ) ° v (X(p) i ° 5 )}

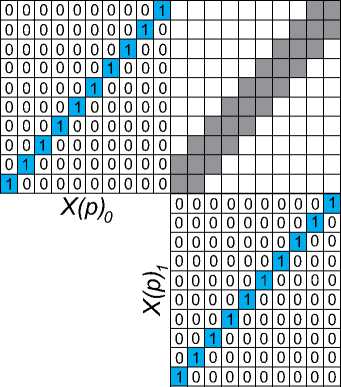
Рис. 3. Зависимость выходного ряда от входных комбинаций позиционного кода

Одной из концепций реализации весового элемента является возможность использования универсальных преобразовательных процедур на элементах пороговой логики. Представленный на рис. 1 весовой элемент имеет вход X(p) , для приема синхронного унитарного сигнала; вход синхронизации syn , и управляющий вход µ , являющийся сигналом от «учителя» в случае обучения на основании определенной выборки с априорной информацией о принадлежности объекта к определенному классу, либо сигналом, поступившим с устройства настройки веса в режиме самообучения. Выходной сигнал С(р) является преобразованной величиной, дальнейшая обработка которого сводится к комбинации с другими сигналами на входе порогового элемента, выполня-

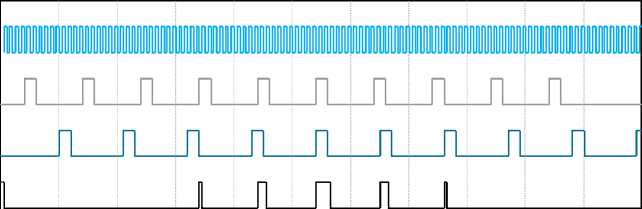
d(SYN)

d(IN1)

v(IN2) (V)

v(OUT) (V)

Рис. 4. Выходная характеристика комбинаций позиционных рядов

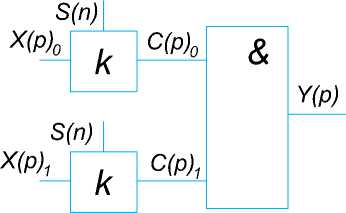
Рис. 5. Конъюнктивный пороговый элемент с k – весовыми элементами Процедура преобразования:

Y(P) ^ {(X(P) o ° k) ° v (X(p) i ° k)}

ющего роль сумматора и активационной функции.

Каждая связь данного нейрона реализуется при помощи управляемого модуля операторами логической свертки сигнала, операция которого задается управляющим сигналом.

В данном случае логическое описание результата преобразования такого нейрона можно описать формулой:

/=<> ,=o где X(p)i p– входной сигнал, задержанный на величину синхроимпульса; U — логическая операция, выполненная из набора {∧, ∨, ⊕, ▷, ◁} – функционально полного набора логических операций, реализуемого комби-

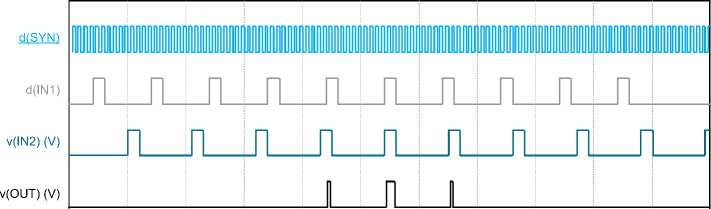
Рис. 7. Выходная характеристика комбинаций позиционных рядов

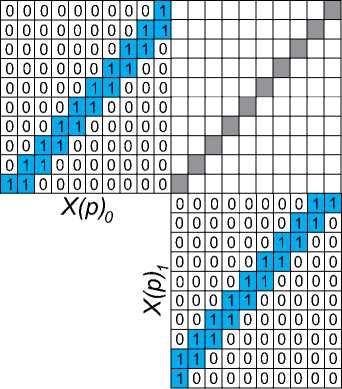
Рис. 6. Зависимость выходного ряда от входных комбинаций позиционного кода

национными схемами простейшей пороговой логики.

Таким образом, полученный элемент является техническим аналогом математической модели нейрона, выполненным на операторах логической свертки сигнала.

Рассмотрим более подробно простейшие операторные модели нейрона с двумя входами, весовыми элементами и логической функцией конъюнкции на выходе ( рис. 2 – 10 ).

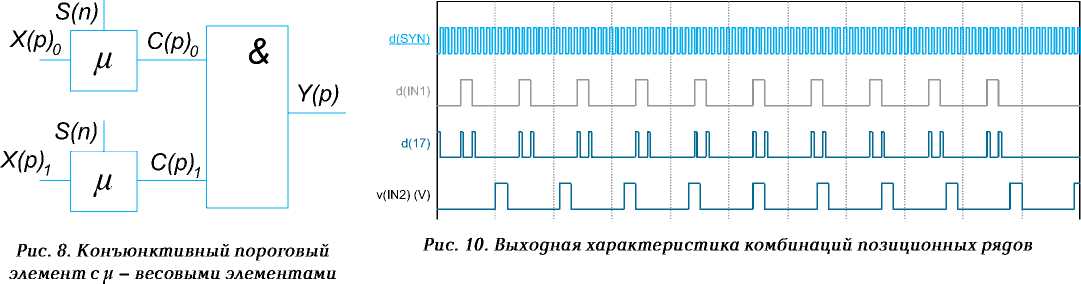
Процедура преобразования:

Y(p) ^ {(X(p) o = p) = v (X(p) i о p)}

чества входных унитарных последова- срезу, преобразование длины и др. Од-

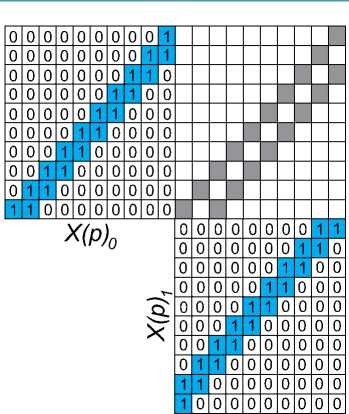
Рис. 9. Зависимость выходного ряда от входных комбинаций позиционного кода

тельностей, а так же от вида смешивающего элемента.

На сетях, построенных с применением данных элементов можно проводить такие функции логического преобразования как: модуляцию и демодуляцию, селекцию, обнаружение «совпадения», выбор минимальных и максимальных значений сигналов, преобразование частот, определение соотношений «опережение – отставание», конвертирование фазоимпульсного сигнала в широтно-импульсный, обнаружение рассогласования, ограничение длины сигнала по фронту или