Isochronous and Anisochronous Modulation Schemes in Wireless Optical Communication Systems

Published Online July 2012 in MECS

The optical channel is usually treated as an Intensity Modulation and Direct Detection (IM/DD) channel [1]. For IM/DD, The modulation OOK (On-Off Keying) is the simple and widely adopted modulation scheme used in commercial FSO communication systems because of ease in implementation, simple receiver design, bandwidth efficiency and cost effectiveness [2]. On the other hand, higher average power efficiency can be achieved by employing Discrete

Pulse Time Modulation (PTM) schemes in which a range of time dependent features of a pulse carrier may be used to convey information.

Discrete (digital) pulse time modulations (PTM) techniques fall into two categories, namely isochronous and anisochronous. Isochronous schemes encode data by varying the position or width of a pulse, but the overall symbol structure remains constant, in contrast, anisochronous schemes have no fixed symbol structure [3], a simple Digital Pulse Time Modulations (PTM) tree is shown in Fig. l.

Digital Pulse Time Modulation (PTM)

Isochronous

Anisochronous

PPM MPPM DPWM PCM

DPIM DPIWM DPPM

RZ

NRZ

Figure. 1 Digital Pulse Modulations Tree

In this paper we will try to make a comparative analysis between isochronous and anisochronous modulation categories presented by PPM (Pulse Position Modulation) and DPIM (Pulse Interval Modulation) respectively. This comparison is made to understand the basic characteristics of each modulation family, what features make such modulation category desirable and which one outperform the other depending on the circumstances and the desirable requirement of the wireless optical communication system. Symbol structures for the modulation schemes and simulation results about the normalized average power requirement, transmission capacity and band utilization efficiency will be presented.

The paper is organized as follows: section two gives the mathematical models of DPIM and PPM including a review on the OOK which will be use just as a benchmark to compare the power efficiencies of the modulation schemes, section three presents the numerical simulation results and discussion with a general comparison between the modulation schemes, where the band utilization efficiency, the power requirement and the transmission capacity will be discussed, this is followed in section four by a conclusion.

Figure. 2 Example of OOK coding

In this paper OOK will be used as a benchmark to compare the power efficiencies of the modulation schemes. To simplify the analysis, we make the high SNR assumption that the BER is dominated by the two nearest signals, the system bit error rate BER can be expressed as:

BER = Q

d min

. 2 П

Where d min is the minimum Euclidean distance between any pair of valid modulation signals (symbols), defined as:

II. MODULATION SCHEMES

The choice of the modulation format is the principle factor in realizing a high performance wireless optical communication system at a reasonable cost and acceptable complexity. For this reason, several modulations and/or encoding schemes have been proposed, which vary symbol structure and the number of slots per symbol. In this section OOK, PPM and DPIM will be introduced.

2.1 On off keying (OOK)

Among all modulation techniques based on intensity modulation with direct detection, OOK is the simple and widely adopted modulation scheme used in commercial FSO communication system because of ease in implementation, simple receiver design, bandwidth efficiency and cost effectiveness [2].

The binary information sequence can be mapped directly to a sequence of light pulses at the transmitter according to the rule: if the information bit is 1, transmit a laser pulse; if it is 0, transmit nothing (Fig. 2) Therefore, there is a one-to-one correspondence between 1’s in the data-stream, and the occurrence of light pulses emanating from the transmitter.

The envelope for OOK is given by:

d

2 min

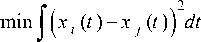
And N 0 is the power spectrum of the Gaussian noise added by the channel.

Assuming Maximum Likelihood (ML) detection, the minimum distance between the two signals in the OOK signal set and the BER are respectively:

dook

2 P

D

BER = Q

(

I

A

The power required by OOK to achieve a given BER and the power required by any other modulation scheme to achieve the same BER are, respectively:

P ook = V N 0 D" Q ^{- 1}( BER )                     (6)

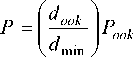
f P, for t e 0, T1 P(t) 4 ^{,          1 ,} ]

|_  0, elsewhere

These relations are used under the assumption that the SNR is high enough that (2) is accurate. Therefore, in the remainder of the paper, the distance ratio d ooK /d min will be used to characterize the power requirements of any modulation scheme.

P c : is the peak power.

2.2 Pulse Position Modulation (PPM)

Nearly all PTM schemes are suitable for optical communication systems. Among them, PPM is a

technique that achieves higher average power efficiency than OOK at the expense of an increased bandwidth requirement [4].

The transmit pulse shape is given by:

| P, for t ^G [ (m-1)T/M, mT/M ]           ^

I       0, elsewhere

Where m= {1, 2 … M}.

Pulse position modulation (PPM) is a modulation method that had been proposed to increase the transmission efficiency in optical communications systems. In PPM, the information is transmitted as follows, each symbol duration T= log 2 (M)/R b is partitioned into M sub-intervals, or slots of duration T/M , and the transmitter sends an optical pulse during one of these slots.

At the receiver side, the receiver detects the encoded PPM symbols by determining which of the M slots contains the laser pulse, and performs the inverse mapping operation to recover the bits stream. An example of PPM mapping is shown in table 1.

A PPM signal can be expressed as:

E n — 1    Г kT A

C_kP 1 1 — — I                  (9)

k = 0 ^k ( N )

Where [c o , c 1 …cn -1 ] is the PPM code word, and where P(t) is a rectangular pulse of duration T/M and unity height. All of the signals are equidistant, with:

Beside the rapid decline of bandwidth efficiency as M increase, the use of PPM increases the system complexity compared to OOK, since both slot and symbol synchronization are required in the receiver, which are critical to system performance [6].

• 2.3 Digital Pulse Interval Modulation (DPIM)

Digital pulse interval modulation (DPIM) scheme is a modified version of the Pulse Position Modulation (PPM), it displays a higher transmission capacity by eliminating all the unused time slots from within each symbol and give build in symbol synchronization ability. Therefore DPIM requires no symbol synchronization since each symbol is initiated with a pulse [7].

d ² = 2 MP ^{2 log} 2 M                          (10)

Therefore, the normalized average power requirement is approximately:

P PPM P _OOK

Mlog M

The bandwidth, B , required by the PPM scheme to achieve a bit rate “ D ”, is approximately the inverse of one chip duration [5]. Then, one can write:

In DPIM, instead of coding the data sequence by the location of the position of a pulse in a fixed frame width, the data sequence is coded such that it is represented by the time interval between the previous and the present pulse. A symbol which encodes b bits of data is represented by a pulse of constant power in one slot followed by k slots of zero power, where (1 ≤ k ≤ M) and, M = 2^b.

DPIM signal can be as:

BPPM

= M D log2 M

x (t ) = 2 a Ф k =-^

k - 1

t - T s (2 k + 2 S m )

m =-m

Where:

This paper defines the band-utilization efficiency, η , as the ratio of D to B , i.e.

ф ( t ) = l^ipp ( t )

is the unit-energy

D     log 2 ( M )

4PPM    TV             . ,

B PPM      M

rectangular pulse of duration T/(M+1) and amplitude of a [8]. T a s is the slot duration and S (S m < S) is the stochastic random data sequence representing data coded into the DPIM symbols.

For the modulation DPIM the minimum and the

maximum symbol lengths are 2Ts and (M+ l) Ts

Table . 1. Examples of the assignation of bit patterns to pulse patterns (DPIM and PPM)

Source data 4-DPIM 1GS 4-PPM 00 01 10 11 П . . , , respectively. So the mean symbol length is given by: (M+ 3) Ts/2.

Assuming the DPIM modulation system encodes b bits data per symbol, let the slot duration is chosen such that the maximum symbol duration is equal to the time taken to transmit b bits of data using OOK, so the slot duration is given as Ts = T/(M+1).

The transmitted optical power is also varied but the average transmitted optical power could be calculated according to the mean symbol length. In (13), a is chosen so that the average optical power is P (at mean symbol length), so we have:

Table. 2. Bandwidth and power efficiencies for various modulations

power efficiency Spectral efficiency PPM 2 Mlog M log2(M) M DPIM л M + 1 4 log2 M ( m + 3)42 M + 3 2log2M a = L + 3 p^- = (M + 3)dook  log2 M

2 V M + 1          4    V M + 1

4a d nn к

M + 3

log₂ M

d min   4 ² 2 a

Therefore, the normalized average power

requirement is approximately:

For the DPIM, we have defined a frame as the interval from the end of the previous pulse to the end of the present pulse, it can be seen that, if an error occurs such that a pulse is missed or a non-existing one is detected, then the PIM data stream will be resynchronized on the detection of the next pulse, this error will produce two erroneous DPIM intervals, since each PIM pulse is used to define an end or start point on two separate frames.

₄ ^M

P DPIM      log 2 M

P ook   ( M + 3)42

We assume that the transmitter conveys information at the rate of bits/s. Each symbol has b bits and b = log 2 M. For DPIM, note that the data rate is not a constant; we have to use the average bit rate based on average symbol rate. So the bandwidth required to support communication at a bit rate based on the average symbol duration, is given as:

• III.    NUMERICAL RESULTS AND DISCUSSION

  • 3.1    Transmission capacity

The transmission capacity of such modulation scheme can be expressed in terms of the number of bits which can be transmitted during the time required to transmit b bits using OOK modulation. PPM has the same transmission capacity as OOK [9] but PPM is more power efficient.

B DPIM _ ^{M + 3}

D    2log₂ M

In DPIM modulation scheme the symbol length is variable and is determined by the information content of the symbol, and in order to avoid symbols in which the time between adjacent pulses is zero, an additional guard slot (Inter Symbol Gap “ISG”) will be added to each symbol immediately following the last pulse. An example of DPIM symbol structure is given in Tab 1.

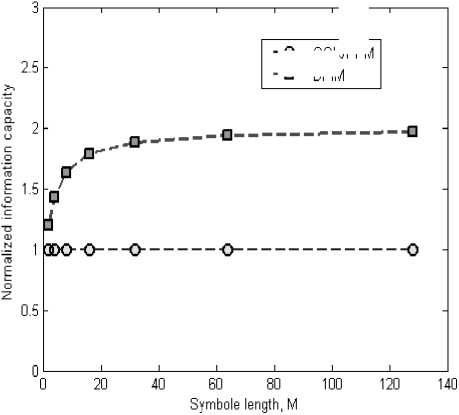
Figure. 3 Normalized information capacity of DPIM and DPPM versus the modulation level

-O-OOK/PPM

Assume the transmission capacity of OOK is M , the symbol time is T sook . And the mean of DPIM symbol time will be:

T sDPIM

M + 3 _т 2( M + 1) sOOK

The transmission capacity of DPIM will be:

т        2 b (2 ^b + 1)

T sOOK

CDPIM =T    =

T sDPIM     2+

Thus:

_ 2 b ( M + 1 )

DPIMM

The transmission capacity of DPPM modulation can be expressed as,

C DPPM

2b 2b b (M +1)

Since the average symbol length of DPMI with no guard slot has only half the length of a PPM symbol, the transmission capacity of the DPIM will increase as M increase.

Fig.3 shows the DPIM and OOK/PPM transmission capacities versus M . From the figure we can see that DPIM modulation offers a higher transmission capacity compared to PPM. Based on the figure, when M is large enough (≈128), the transmission capacity of DPIM will approach to 2M , twice of the OOK/PPM.

The DPIM modulation displays a higher transmission capacity compared to PPM modulation, since conversion is reinitiated immediately after the previous count value has been established; no additional time is wasted waiting for the expiry of a longer predetermined counting period.

The improvement is transmission capacity can be employed to improve either the power efficiency or the bandwidth efficiency of the system. The same average data rate can be supported with approximately half the slot frequency of PPM, therefore, improving the bandwidth efficiency of the modulation scheme although the power efficiency would be reduced due to the increased duty cycle.

Alternatively, a higher number of bits per symbol could be supported without an increase in slot frequency, thereby improving the power utilization efficiency.

• 3.2    Power requirements and Band width efficiency

The two constraints in wireless optical communications systems are: lower power consumption due to battery powered portable system, and lower band width requirement, where large area detectors used in the diffused system have large capacitance limits the receiver bandwidth.

Symbols length, M

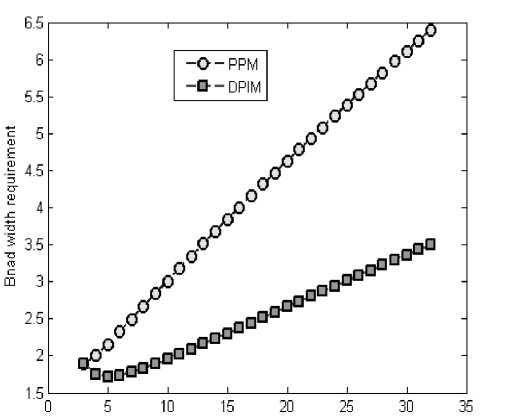
Figure. 4 Band width requirement of PPM and DPIM

Therefore, the modulation schemes used should have high power and spectral efficiency. The bandwidth and power efficiency normalized to OOK for the PPM and DPIM are listed in Tab.2.

Fig.4 presents the bandwidth requirements of PPM and DPIM under a wide range of the operating symbol length M. According to the figure, increasing the symbol length results in an increase in the bandwidth requirement (i.e. decreases the bandwidth efficiency and the allowable bit rate) for both PPM and DPIM with an advantage to DPIM. This leads to a decrease in the required average power (i.e. enhances power efficiency) as shown in Fig. 5 where PPM requires the least average optical power.

Fig.5 shows the power efficiency comparisons of DPIM, PPM in dB. We can see that the DPIM has lower power efficiency than PPM and this deference increases as M increase. Where in the case of M = 32, the DPIM requires approximately 2.6 dB more power than the PPM modulation. Which proofs that isochronous modulation are powerful in term of power efficiency and poor in term of spectral efficiency compared to anisochronous modulations.

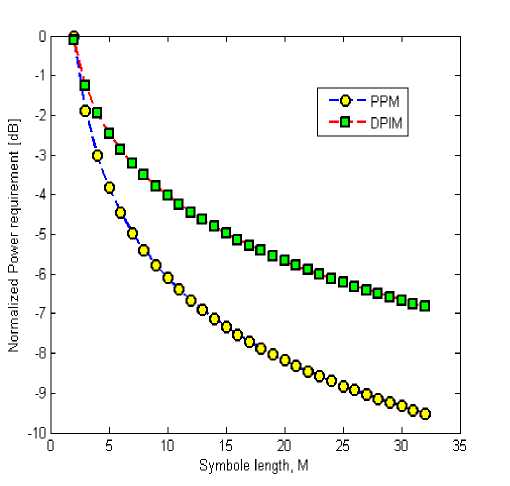
Figure. 5 Normalized average power requirement of PPM and DPIM

• IV.    CONCLUSION

In this paper, we have compared the transmission capacity, the spectral and the power efficiencies of two popular modulation schemes in optical wireless communication systems; PPM and DPIM in order to give a wide view about two modulation families that are suitable for optical wireless communication systems; isochronous and anisochronous modulation schemas.

PPM has poor clock recovery and resynchronization characteristics, since both slot and symbol synchronizations are required at the receiver, unless a framing pulse is used to mark the beginning of each modulated sequence; however this would increase the power requirement by a factor of two. Unlike PPM, DPIM does not require symbol synchronization since each symbol is initiated with a pulse, thus resulting in a much simplified receiver structure. Furthermore, DPIM displays a higher transmission capacity by eliminating all the unused time slots from within each symbol. It is concluded that the main advantage of anisochronous modulation schemes is the symbol synchronization ability which makes its strong candidates when synchronization comes into account, beside that; anisochronous are the most efficient scheme in terms of transmission capacity and band width requirements. And when it comes to power performance, isochronous modulations are more efficient.

For anisochronous modulations, note that the data rate is not a constant. To permit the continuous transmission of data, buffers will be required in both the modulator and demodulator to interface between the binary data stream and the variable frame width of the modulation signal.