Использование алгоритма ожидания и максимизации правдоподобия в марковской модели непрерывного профиля для синхронизации сигналов манипулятора

• I.    Манипулятор на основе прецизионного акселерометра

В данной работе рассматривается задача восстановления управляющего сигнала манипулятора, чувствительным элементом которого является прецизионный акселерометр [1]. Внешний вид манипулятора показан на рис. 1.

Рис. 1. Внешний вид манипулятора

Это устройство представляет собой манипулятор нового поколения. Он способен отслеживать вращательные движения руки оператора и использовать их для позиционирования курсора компьютерной мыши. Ключевым элементом устройства является прецизионный акселерометр типа MEMS (Micro–Electro–Mechanical System) (рис. 2).

Так как акселерометр обладает чувстви- тельностью к земной гравитации, то изменение его положения относительно направления ускорения ~g силы тяжести приводит к изменению значений проекций этого ускорения на чувствительные оси акселерометра x, y , z . Значения этих проекций используются для формирования управляющего сигнала.

Акселерометр, как и вся электронная часть устройства, помещена в корпус, который крепится на руке оператора. Таким образом, посредством наклонных движений руки производится позиционирование курсора компьютерной мыши.

Блок-схема, демонстрирующая принцип работы устройства, изображена на рис. 3. Аналоговые значения проекций ускорения периодически выбираются и конвертируются при помощи АЦП в набор цифровых выборок a x (n), a y (n), a z (n). Далее микроконтроллер производит цифровую обработку полученного сигнала и преобразует его в сигнал для позиционирования курсора компьютерной мыши.

Данные записываются с двух независимых акселерометров, установленных на печатной плате манипулятора. Так как в цепях питания акселерометров присутствуют электрические шумы, а также из-за неточной калибровки датчиков показания акселерометров могут отличаться друг от друга. Для восстановления управляющего сигнала манипулятора в данной работе используется марковская модель непрерывного профиля, параметры которой оцениваются при помощи алгоритма ожидания и максимизации правдоподобия.

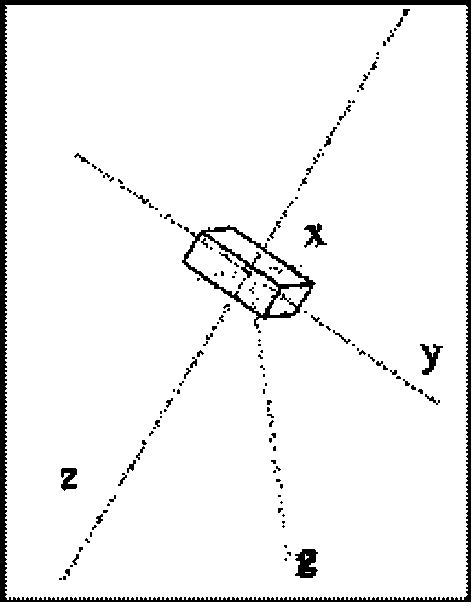
Рис. 2. Три чувствительных оси MEMS-акселерометра и ускорение ~g силы тяжести

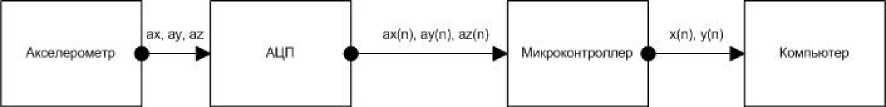
Рис. 3. Блок-схема управляющего контура дистанционного манипулятора

• II.    Марковская модель непрерывного профиля

Рассмотрим набор из K временных рядов xk = (xk, xk, ..., xNk). При этом частота дискретизации не обязана быть одинаковой для различных временных рядов из данного набора. Более того, она может не быть постоянной в пределах одного временного ряда ~xk . Для удобства считаем, что Nk = N для всех к. Данное ограничение не является требованием данной модели. Ее можно распространить и на случай различных Nk . Модель непрерывного профиля задается следующим образом: предполагается, что существует скрытая последовательность, z = (zi, Z2, ..., zm), каноническое представление набора зашумленных входных данных [2]. Любой временной ряд из данного набора моделируется как неравномерно во времени формируемая версия скрытой последовательности, к которой применены локальные преобразования масштаба. В идеальном случае M должно быть бесконечно большим, чтобы точки любого временного ряда могли быть отображены в соответствующие точки скрытой последовательности. На практике используется M = (2 + e)N, где Е < 0,2. В силу того, что длина скрытой последовательности больше, чем длина наблюдаемого временного ряда, наблюдаемое время может быть эффективно ускорено или замедлено. Локальное масштабирование, используемое при генерации каждого наблюдаемого временного ряда, задает- ся последовательностью скрытых состояний. Обозначим последовательность скрытых состояний для k-го временного ряда как ~πk . Каждое состояние из последовательности скрытых состояний состоит из состояния времени и состояния масштаба: πik → {τik,ϕik}. Состояния времени могут принимать целые значения в диапазоне (1, ..., M), состояния масштаба принадлежат упорядоченному набору (^1, ..., ^q). В описываемом эксперименте используется Q = 7 равноудаленных состояний в логарифмическом масштабе. Распределение вероятности элемента xik при условии скрытого состояния nk задается выражением: Ak (xk\~) = p(xk|nk, Z, о, uk) = N(xk; zTk^kuk, ст2), πi                                                        τi где N(x; ц, ст2) — плотность вероятности нормального распределения случайной величины x со средним значением ц и дисперсией ст2, uk — вещественные масштабные коэффициенты, каждый такой коэффициент является уникальным для временного ряда. Для того чтобы полностью определить данную модель, необходимо задать вероятности переходов из одного состояния в другое. Распределение вероятности переходов для состояний масштаба и состояний времени являются независимыми. Поэтому вероятность перехода из состояния πj в состояние πi задается выражением: Tk,ni = p(ni\nj) = p(^i\^j)pk(Ti\Tj). На модель накладывается дополнительное ограничение, что из данного состояния времени нельзя перейти более чем на J состояний вперед. Подобное ограничение существует и для переходов между состояниями масштаба. Из данного состояния масштаба возможны переходы только в соседние состояния. Данные ограничения обеспечивают сокращение времени работы алгоритма. Каждый наблюдаемый временной ряд имеет свое рас- пределение вероятностей переходов из одного состояния времени в другое состояние времени.

Распределения вероятности переходов из одного

состояния в другое для состояний времени и

состояний масштаба являются полиномиальными:

p ^k (r i = a \ T i - i = b) = <

d k , если a — b = 1, d k , если a — b = 1,

.

.

.

d J , если a — b = J,

0, иначе;

и

p(^ i = a \ ^ i — i = b) = <

• s o ,    если D(a,b) = 0,

• s i ,    если D(a,b) = 1,

s i , если D(a,b) = — 1,

0, иначе соответственно, где D(a,b) = 1 означает, что а на одно состояние масштаба больше, чем b, D(a,b) = —1 означает, что a на одно состояние масштаба меньше, чем b, и D(a,b) = 0 означает, что а = b. Условия нормировки: 2si + so = 1 и PJi dk = 1.

• III.    Обучение модели посредством алгоритма ожидания и максимизации правдоподобия

Для оценки параметров модели используется алгоритм ожидания и максимизации правдоподобия (EM-алгоритм) [3, 4]. На E -шаге используется алгоритм прямой и обратной рекурсии [5]. Этот алгоритм позволяет вычислить следующие условные вероятности: Y k (i) = p(n i = s \ ~) и £ s,t (i) = p(n i — i = s,n i = t \ x ^k ). На M -шаге оцениваются параметры модели. Логарифм правдоподобия K наблюдаемых временных рядов ~ ^k задается выражением: L ^P = L + P , где L — логарифм правдоподобия в скрытой марковской модели, и вычисляется посредством алгоритма прямой и обратной рекурсии, P — логарифм правдоподобия, отвечающий за априорные ограничения, наложенные на модель. Выражения для составляющих логарифма правдоподобия:

KNN

L = X log Р(п1) + Xlog Ani (xk\~) + Xlog Tk-i ,ni , k=i               i=i

T-1

P = — A X (z j +i — Z j ) ² + X log D(d k \{ n k } )+log D(s v \{ n V } ).

j=1

Первая составляющая P соответствует ограничению, связанному со сглаживанием скрытой последовательности, параметр λ контролирует степень сглаживания скрытой последовательности. Второй и третий члены отвечают за ограничения, наложенные на вероятности переходов из состояния в состояние, соответственно для состояний времени и масштаба. Параметры n k и nV — параметры распределения Дирихле. Данное ограничение необходимо для того, чтобы отличные от нуля вероятности переходов оставались ненулевыми. Обозначим через S общее число возможных состояний, тогда ожидаемый полный логарифм правдоподобия:

< L P >  п = P + P K _1 P S .1 Y* k q1) log T ^, + P K .1 P S =1 P N =1 Y k (i) log A . (x k | ~) + ...      .

... + Pt 1 P S .1 P S 0 .1 P N    . (i) log T ,^ ,                                           ( '

где T k_s = p(n 1 = s), Y k (i) и ^ k _s 0 (i) — условные вероятности, определенные посредством алгоритма прямой и обратной рекурсии. Оценки значений параметров модели получаются взятием производных по данным параметрам от математического ожидания логарифма правдоподобия (1) и приравниваем их к нулю. Для вычисления оценок значений для точек скрытой последовательности, получаем систему из M уравнений:

∂ < L ^P >  π

∂z j

_K E N =i [ 7 k ( i ) ^ s u k ( xk - Zj^

= 0 = X     X k = 1             {s|Ts=j}

—A(4z j — 2z j _— 1 — 2z j +1 )

для j = 1, ..., M.

Для случаев j = 1 и M соответственно члены Z j _— 1 и Z j+1 равны нулю. Получаем систему из M уравнений с M неизвестными. При этом каждое уравнение содержит только три элемента скрытой последовательности. Решая линейную систему уравнений с трехдиагональной матрицей, получаем скрытую последовательность. Аналитические формулы для ст ² и u k :

„2_ P S .1 P ,i =1 Y ,‘ (i)(x k — Z T s U ^k .

N             ’ uk = PS=1=T,.1 P' Yk(i)xk

P S =1 (z T s y . ) ² P" 1 Y k (i).

Выражения для оценок вероятностей переходов для состояний времени и состояний масштаба:

^k d _v

,        q      ENy € 00 (i)

_n k ₊ P S P i =² ,,, ⁿ v “T 2=1=1 2={_s⁰ I t , 0 — T , = v }

PJτ  k  PJτ PS P j=1 nj + 2=1=1 2= 1=1 2={.\t,o

— ■

T , = j } PE (i) ,

s v

n j + P K =1 P S =1 P _{ 1 00 c h (1,V) } P ,=2 ^ k. 00 (i)

P 1=0 n j + P K =1 P S =1 P _{ 1 00 _G H ( s, 1) ,H ( 1, 0) } P ,=2 ^ k,i 00 (i)

Выражения для оценок параметров ст ² , u ^k , z связаны между собой. Поэтому необходимо задать последовательность, в которой будет происходить оценка этих параметров. В работе использован следующий порядок вычисления: ст ² , z, u ^k . Два других параметра d k , s v никак не связаны между собой. Следует также отметить, что не используется нормировка в выражениях для распределения Дирихле, а также в показателе степени отсутствует минус единица: D(d* k \{ n^k } ) = Q J = 1 (d ^k ) ⁿ v , D(s v \{ n V } ) = Q V =o (s v ) ⁿ v . Макет программной реализации метода модели непрерывного профиля описан в [6].

• IV.    Синхронизация сигналов манипулятора

В данной работе проведен следующий эксперимент: произведена запись управляющих сигналов манипулятора одновременно с двух независимых датчиков ускорения при выполнении произвольного движения руки с данным манипулятором. При этом акселерометры имеют независимые цепи питания и независимые сигналы тактовой частоты. Запись сигналов производится только для одной чувствительной оси акселерометров. Полученные сигналы не синхронизованы во времени, а также имеют различную величину (рис. 4).

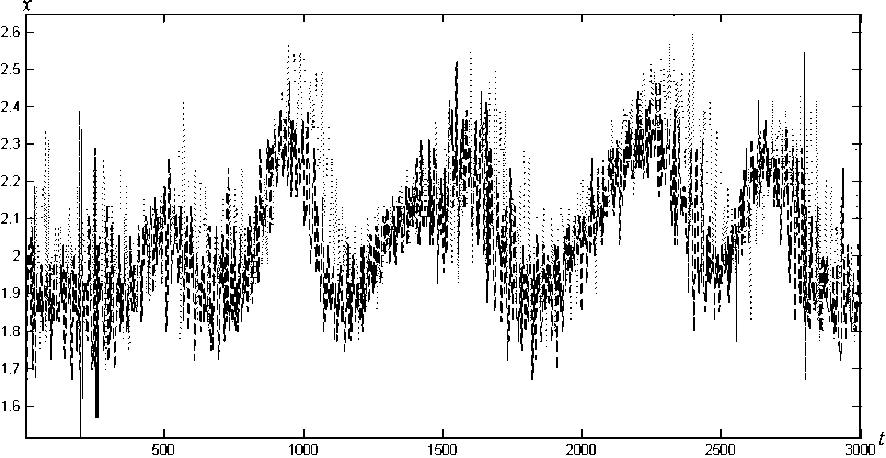
Рис. 4. Временные зависимости проекции ускорения x = x ( t ) , полученные для двух независимых датчиков. Точками обозначен сигнал с первого акселерометра, а пунктиром — со второго

х

500               1000              1500              2000              2500              3000

Рис. 5. Временные зависимости x ⁰ = x ( t )

Различия в величине сигналов вызвано несколькими факторами. Главные из них: неточная калибровка датчиков; шумы в цепях питания акселерометров; неточная установка датчиков, которая приводит к некоторому постоянному сдвигу в сигналах датчиков. В силу того что акселерометры используют независимые тактовые сигналы, которые не синхронизованы, в записях сигналов также наблюдается рассинхронизация.

Сигналы переведены в энергетический диапазон значений следующим образом:

P 2_ 1L ( w ( L + 1+ k ) x ( iL + k ) ) 2

• x ⁰ (i) = —=—²---- l          , где w — оконная функция Ханна, L — размер окна Ханна [7,

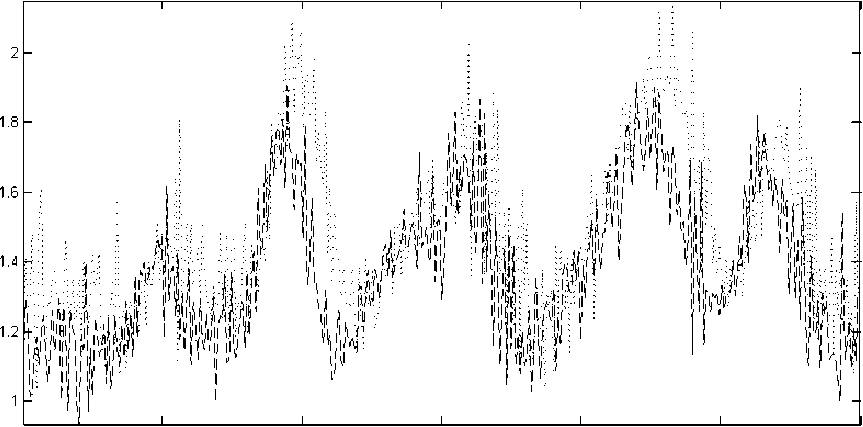
• 8]. В данной работе используется значение L = 8. Чтобы длина синхронизованных сигналов совпадала с длиной исходных сигналов, используется линейная интерполяция. Полученные сигналы показаны на рис. 5.

  

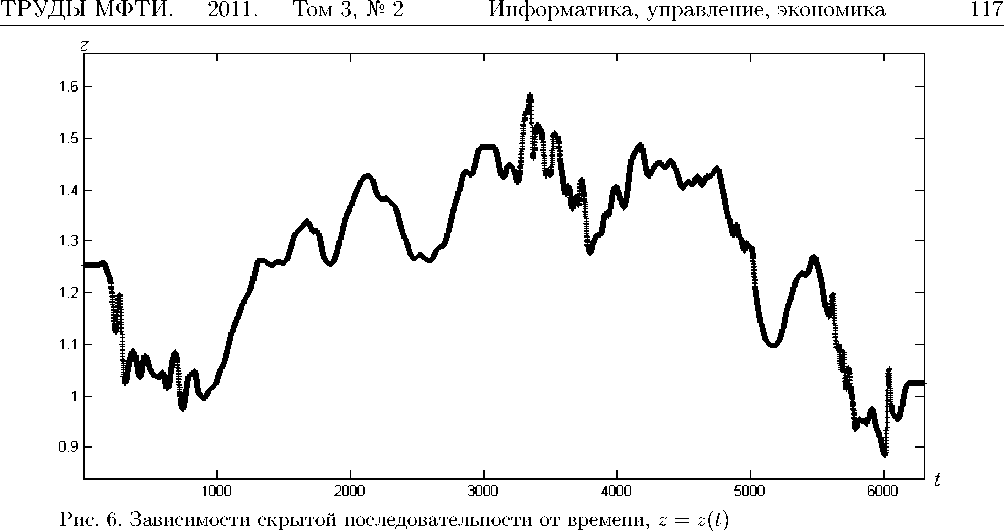
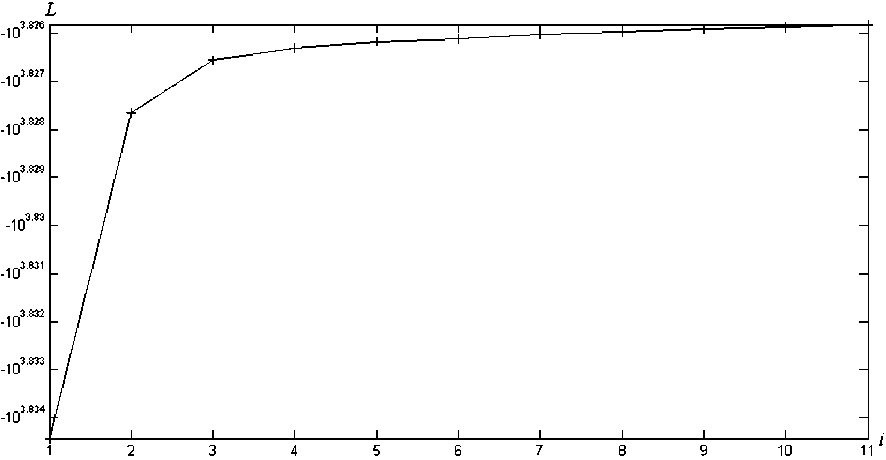
Рис. 7. Зависимость логарифма правдоподобия от числа итераций

Преобразованные сигналы x ⁰ = x ⁰ (t) прошли процедуру выравнивания при помощи марковской модели непрерывного профиля. Скрытая последовательность для данного набора из двух сигналов показана на рис. 6.

Обучение модели производилось при помощи алгоритма ожидания и максимизации правдоподобия. Этот алгоритм демонстрирует достаточно хорошую сходимость, что видно из графика зависимости логарифма правдоподобия (1) от номера итерации (рис. 7).

После обучения модели при помощи алгоритма ожидания и максимизации правдоподобия произведена синхронизация сигналов (рис. 5) при помощи алгоритма Витерби [9, 10]. Результат синхронизации сигналов изображен на рис. 8.

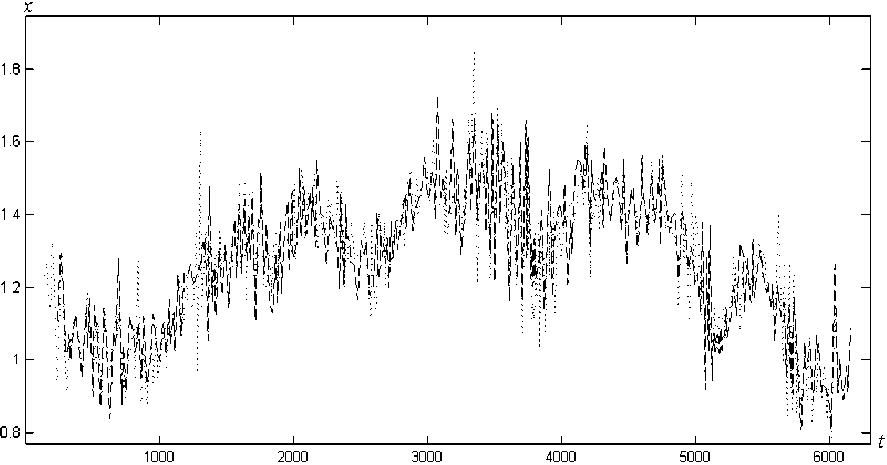
Рис. 8. Результат выравнивания сигналов