Использование априорной информации для построения полиномиальных моделей комплекса "судно-трал"

• 1.    Введение. Постановка задачи и методы решения

Натурные испытания судовых комплексов требуют вывода судна из нормального режима эксплуатации и связаны со значительными затратами времени, трудовых и материальных ресурсов. В то же время натурным испытаниям судового комплекса предшествует, как правило, большое количество теоретических и экспериментальных исследований отдельных его частей. Поэтому с целью сокращения объема экспериментальных исследований и правильной их организации для построения математических моделей необходимо максимально использовать эту априорную информацию.

Большую информацию об объектах управления содержат в себе экспериментальные данные, полученные в процессе ранее проводимых испытаний судового комплекса или его отдельных частей. Результатами этих испытаний, как правило, являются множества статических характеристик, каждая из которых связывает два-три, иногда четыре параметра.

Графическое представление взаимосвязей между отдельными параметрами элемента или системы обладает большой наглядностью. Однако, анализ большого количества кривых, расположенных на отдельных рисунках, выбор оптимальных режимов работы системы крайне затруднен без использования ЭВМ. В связи с этим возникает задача ввода графической информации в память машины.

Более рациональным решением данной проблемы является математическое представление исходной графической информации, т.е. аппроксимация статических характеристик математическими выражениями в виде полиномов, и введение в память машины коэффициентов этих выражений.

• – механические характеристики приводных электродвигателей ваерных лебедок и т.д.

• 3.    Особенности использования методов планирования эксперимента при аппроксимации статических характеристик

Математическое описание статических характеристик, связывающих три и более параметров, является сложной задачей. Предлагается использовать для этой цели методы планирования активного эксперимента.

Аппроксимация семейства статических характеристик производится обычно полиномом второго порядка вида k k k y = b0 + ∑ bixi + ∑ bijxixj + ∑ bii xi2. (1) i=1 i≠j i=1

Для определения коэффициентов полинома проводится эксперимент, под которым в данном случае понимается определение значений выходного параметра по известной статической характеристике. При этом значения входных параметров в каждом опыте задаются планом эксперимента. Тип плана определяется характером кривых с учетом особенностей использования МПАЭ для решения данной задачи.

Для аппроксимации сложных статических характеристик предлагается использовать ортогональные планы второго порядка (двухфакторный и трёхфакторный) или несимметричные планы типа М×М×М, описанные в ( Вознесенский , 1973).

Для рассматриваемой задачи ортогональный план весьма удобен, так как он позволяет очень просто найти коэффициенты полинома.

Следует отметить, что объектом исследования при использовании методов планирования экспериментов являются процессы, механизм которых, как правило, неизвестен.

Особенностью поставленной задачи является то, что объектом исследования является не сам процесс, а статические характеристики, описывающие этот процесс в установившемся режиме. При этом выходная величина y определяется практически без ошибки, и результаты каждого опыта точно воспроизводятся при его повторении, так как отсутствуют случайные воздействия.

В связи с этим нет необходимости в проверке однородности выборочных дисперсий воспроизводимости, в проведении рандомизации и дублировании опытов. В то же время возникает сложность при проведении оценки значимости коэффициентов и проверке адекватности математической модели в форме полинома; уровни факторов часто оказываются неравноотстоящими. Иначе говоря, факторы x 1 , x 2 ,…, x n не всегда варьируются на уровнях, отстоящих друг от друга через равные интервалы ∆ x i ; не для всех N опытов измерено значение выходного параметра.

Проверка адекватности аппроксимирующего выражения по F -критерию и значимости коэффициентов по t -критерию в данном случае неприемлема, так как дисперсия воспроизводимости при определении значений y по графику практически равна нулю. При этом все коэффициенты, даже мало отличающиеся от нуля, окажутся значимыми, а любое отклонение вычисленного по полиному значения Y от значений y , снятых с характеристики, формально делает модель неадекватной.

Аналогичная проблема адекватности и значимости коэффициентов возникает и при исследовании математической модели объекта на ЭВМ.

В этом случае наиболее приемлемы следующие пути:

• а)    считать все коэффициенты значимыми, так как практически дисперсия опытов отсутствует;

• б)    оценку проводить на основе принятого уровня точности аппроксимации, что связано с искусственным введением дисперсии воспроизводимости. Приняв значение ошибки опыта для выходного параметра, проверку адекватности модели можно произвести по F -критерию.

• 4.    Примеры использования априорной информации об объекте для получения математическоймодели элементов судового комплекса

  
  
  

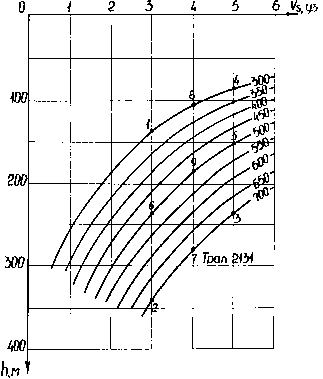
  Рис. 1. Тарировочная диаграмма трала

  
  

  На рис. 1 представлена тарировочная диаграмма трала 2131, которая показывает зависимость горизонта хода трала от скорости буксировки V_s и длины вытравленных ваеров L ( Шишло , 1975) .

Оценку соответствия аппроксимирующего полинома аппроксимируемой кривой или их семейству можно осуществить по максимальному абсолютному отклонению значений выходного параметра, вычисленного по полиному, от значений, определенных по статической характеристике.

Последний путь уступает в математической строгости первым двум. Однако, учитывая наглядность графического описания статических свойств объекта, этот путь вполне приемлем при аппроксимации статических характеристик.

К особенностям использования методов планирования эксперимента для математического представления статических характеристик следует отнести и то, что в этом случае на проведение эксперимента – определение значений выходного параметра по графику – не затрачивается много времени и ресурсов, т.е. эксперимент не является дорогостоящим. Поэтому вопрос о минимизации количества необходимых опытов не стоит так остро, как при планировании промышленных экспериментов . В большинстве случаев нет необходимости в последовательном характере эксперимента, поскольку характер статических характеристик уже известен.

Например, если статическая характеристика показывает, что связь y = f ( x 1 , x 2 ) является нелинейной, то, как правило, нет необходимости в первоначальном использовании более простых линейных планов .

Учитывая определенную сложность оценки адекватности модели, представляется целесообразным использовать нелинейные планы даже в тех случаях, когда нелинейность статических характеристик едва заметна. О степени нелинейности можно судить по величине коэффициентов при квадратичных членах полинома. Нелинейные планы более универсальны.

Введём обозначения независимых переменных: V_s – cкорость судна в кодированных координатах; L s – длина вытравленных ваеров в кодированных координатах. Ограничим описываемую область следующими значениями независимых переменных:

V s ^мин = 3 уз; V s ^макс = 5 уз; L в ^мин = 300 м; L в ^макс = 700 м.

Определим центр эксперимента

Vs0 = (Vsмакс + Vsмин)/2 = 4 уз, Lв0 = (Lвмакс + Lвмин)/2 = 500 м и интервалы варьирования независимых переменных

Δ V s = ( V s ^макс – V s ^мин)/2 = 1 уз, Δ L в = ( L в ^макс – L в ^мин)/2 = 200 м.

Коэффициенты полинома определяются по формулам (2)

9                                             9                                    99

b0= (1/9)∑ yu – 2/3(b11– b22); bii = (1/2)∑ (xiu2 – 2/3)yu; bi = (1/6)∑ xiuyu; bij = (1/4)∑ xiuxjuyu.(2)

u=1                                       u=1                               u=1

Подставив значения коэффициентов в (1) и учитывая принятые обозначения, получим полиномиальную модель тарировочной диаграммы трала.

ĥ = 185,7 – 40,0 V s + 88,3 L в – 14,0 V s L в + 6,5 V s ² + 6,6 L в ², м, где

V s = V s ^абс – 4; L в = ( L в ^абс – 500)/200.

Из табл. 1 видно, что максимальное отклонение расчётного значения от снятого с диаграммы не превышает 2 %. Аппроксимацию можно считать приемлемой. В противном случае следует уменьшить радиус обследуемой сферы, т.е. диапазон варьируемого участка.

Полином второго порядка с успехом можно использовать для аппроксимации многих статических характеристик и таким образом сократить объем собственных экспериментальных исследований.

На рис. 2 показана зависимость избыточной тяги судна, т.е. тяги, используемой для буксировки трала, от скорости судна и мощности гребного электродвигателя БМРТ Т = f ( V_s , N _гэд).

Для математического представления данного семейства кривых использован ОЦКП второго порядка (табл. 2).

Таблица 1. План эксперимента и расчётная матрица для построения полиномиальной модели h = f ( V s , L )

Номер точки	Уровни факторов					Результаты опытов	Результат расчёта
	x 1	x 2	x 1 2– 2/3	x 2 2– 2/3	x 1 x 2	h , м	ĥ , м	| h – ĥ| , м	| h – ĥ| ,%
1	–1	–1	1/3	1/3	+1	135	136,7	1,7	0,9
2	–1	+1	1/3	1/3	–1	340	340,4	0,4	0,2
3	+1	+1	1/3	1/3	+1	235	232,4	2,6	1,4
4	+1	–1	1/3	1/3	–1	85	84,0	1,0	0,5
5	+1	0	1/3	–2/3	0	150	151,9	1,9	1,0
6	–1	0	1/3	–2/3	0	235	231,9	3,1	1,7
7	0	+1	–2/3	1/3	0	280	279,9	0,1	0
8	0	–1	–2/3	1/3	0	105	103,9	1,1	0,6
9	0	0	–2/3	–2/3	0	185	185,7	0,7	0,4

Таблица 2. Ортогональный центральный композиционный план второго порядка для построения полиномиальной модели Т = f ( N _гэд, V_c )

Опыт	Уровни факторов					Результаты опытов	Расчет
u	x 1	x 2	x 1 2– 2/3	x 2 2– 2/3	x 1 x 2	Т , кгс	Tр , кгс	невязка Δ Т , кгс
I	–1	–1	1/3	1/3	+1	16000	15850	150
2	–1	+1	1/3	1/3	–1	4700	4550	150
3	+1	+1	1/3	1/3	+1	11300	11250	50
4	+1	–1	1/3	1/3	–1	24000	23950	50
5	+1	0	1/3	–2/3	0	20500	20300	200
6	–1	0	1/3	–2/3	0	13000	12900	100
7	0	+1	–2/3	1/3	0	8000	7900	100
8	0	–1	–2/3	1/3	0	20000	19900	100
9	0	0	–2/3	–2/3	0	16700	16600	100

Центр эксперимента задан точкой с координатами

V_s ⁰ = 4 узла; N _гэд⁰ = 1500 кВт.

Интервалы варьирования независимых параметров

∆ V s = 4 узла; ∆ N гэд = 300 кВт.

Проведено девять опытов. В результате определения коэффициентов получен полином

T^р = 16600 + 3700 N гэд – 600 V s –

2100 V² – 350 N гэд V s , кгс,       (3)

где T^р – вычисленные (расчетные) значения избыточной тяги судна.

В табл. 2 приведены значения избыточной тяги Т в точках плана, вычисленные значения T^р и абсолютные значения отклонений Δ Т в этих же точках.

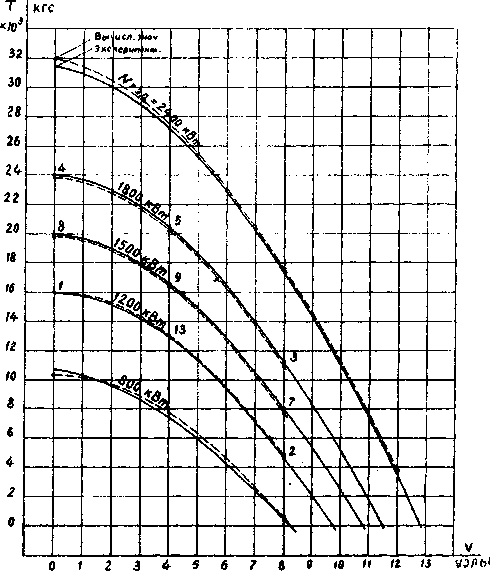
Рис. 2. График зависимости избыточной тяги судна от скорости судна и мощности гребного электродвигателя БМРТ