Использование атрибутивных признаков при спецификации регрессионной модели стоимости квартир

Введение. Для оценки влияния факторных переменных на результативный признак используются различные эконометрические инструменты [1–14]. Например, в опубликованной ранее работе [1] на основании стоимости квартиры в совокупности квартир, предлагаемых к продаже на рынке жилья в г. Красноярске в 2017 г., строится регрессионная модель, в которой в качестве объясняющих переменных (регрессоров) выступают количественные переменные (площадь общая, площадь жилая и др.). В результате получали характеристики, по которым судили о степени влияние какого-либо фактора [1–14]. При изучении совокупности квартир, предлагаемых к продаже на первичном рынке жилья в г. Красноярске в 2017 г. [15], было выявлено, что сильное влияние на стоимость квартиры, помимо количественных признаков, например общей площади квартиры, оказывают атрибутивные признаки: район города, в котором находится дом, и материал, из которого этот дом построен.

Если статистический анализ числовых признаков не вызывает затруднений, то при работе с качественными признаками возникают различные сложности: значение признака представлено словом – атрибутом, необходимо ранжировать совокупность, заменяя каждое значение рангом. Если при ранжировании заменять значения просто порядковыми номерами, то числовое значение будет искажать влияние на результативный признак. Например, при ранжировании по признаку «район» квартирам в Академгородке присвоен ранг 12, а квартирам в Покровке ранг 6. Получается, что квартиры в одном районе в два раза «больше», чем в другом. Возникает вопрос, почему именно в два раза и действительно ли «больше» или это просто неподтвержденная догадка исследователя?

Для исследуемой совокупности [5] предлагается применить новый метод оценки влияния атрибутивных признаков на эндогенную переменную. Выделим два атрибутивных признака: материалы стен и район, в котором построен дом. Разработаем этот метод для совокупности однокомнатных квартир, а затем протестируем его на совокупностях 2-, 3-, 4-комнатных квартир.

Метод фиктивных переменных. При исследовании влияния атрибутивных признаков будем использовать метод фиктивных переменных.

Оценим влияние района ( z ), в котором построен дом, на формирование цены квартиры ( y ) (структура изучаемого явления представлена на рис. 1).

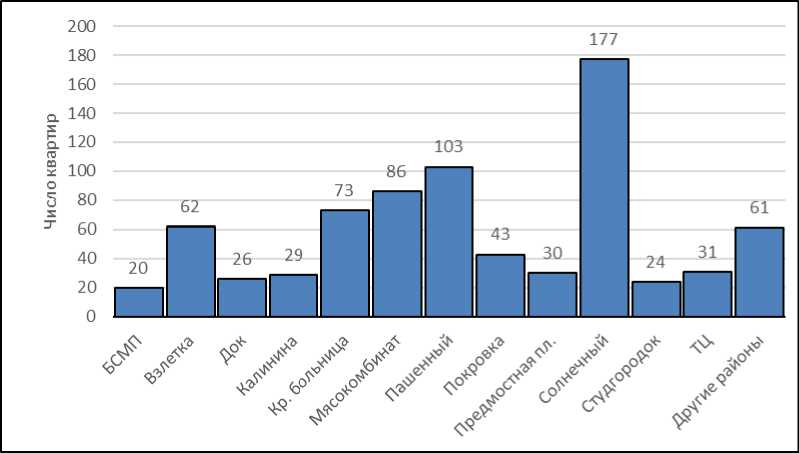
Рис. 1. Распределение предлагаемых к продаже однокомнатных квартир по районам, г. Красноярск, 2017 г.

Fig. 1. Distribution of offered for sale one-room apartments by district of the city Krasnoayarsk, 2017 year

Для учета атрибутивного признака (z) введем в регрессионную модель двенадцать фиктивных переменных z1, z2, …z12. По имеющейся выборке однокомнатных квартир (объем

765 элементов) рассчитаем оценки параметров уравнения регрессии. Уравнение регрессии будем строить в стандартизированном виде:

t =-0,011 + 0,251 -0,081 -0,011 -0,051 -0,301 -0,181 + y zzzzzzz

• - 0,68   ¹     11,78   ²      - 4,43   ³      - 4,63   ⁴      - 2,23   ⁵ - 13,42 ⁶      - 7,55   ⁷

  
  

+ 0,04 t - 0,14 t - 0,44 t - 0,04 t + 0,09 t + 0,60 t .

zzz z z x

1,96 ⁸      - 7,87 ⁹ - 16,5 8 ¹⁰ - 2,42 ¹¹      5,05 ¹² 33,98

где ty – стоимость квартиры (стандартизированная переменная, соответствующая стоимости y - У                                               1

квартиры 1y =-----), Iz , 1z ,.., lz   - стандартизированные фиктивные переменные, sy       12      12

соответствующие   атрибутивному   признаку «район», t _x – общая площадь

(стандартизированная переменная). Для оценки каждого параметра снизу указано наблюдаемое значение t -статистики.

В уравнении (1) скорректированный коэффициент детерминации составил 82,6 %, что говорит о высоком качестве и статистической значимости построенного уравнения.

Для оценки влияния атрибутивного признака ( z ) – «район», на основе построенной корреляционной матрицы рассчитаем совокупный коэффициент корреляции:

r       = в г + + в r = ( - 0,012 ) - ( - 0,029 ) + . + 0,092 ■ 0,268 = 0,404.

y|z 1 z 2 . Z 12 ^1 yz 1                  12 yz 12              ,                   ,                         ,             ,               ,

Доля влияния количественного признака в объясненной вариации составила 51,2 %, а атрибутивного признака – 48,7 %.

Далее, оценим влияние материала стен дома ( u ) на формирование цены квартиры ( y ) (структуру явления отразим на рис. 2).

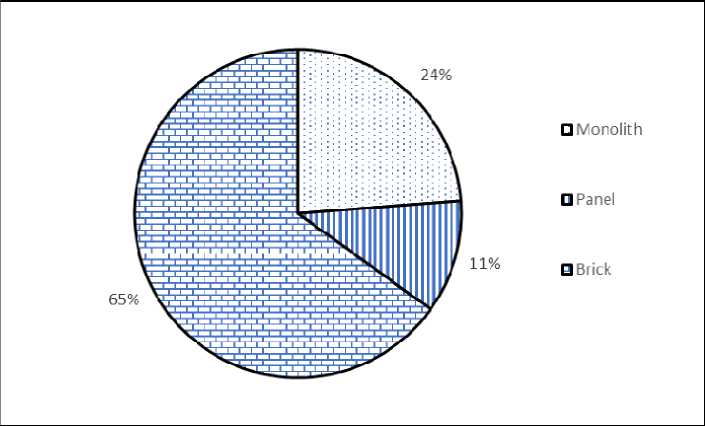
Рис. 2. Распределение предлагаемых к продаже однокомнатных квартир по материалу стен, г. Красноярск, 2017 г.

• Fig. 2.    Distribution of offered for sale one-room apartments by wall material, Krasnoyarsk, 2017 year

Для учета атрибутивного признака ( u ) введем в регрессионную модель две фиктивных переменных u 1 , u 2 . Построим стандартизированную регрессионную модель:

t y = - 0,11 t u + 0,05 t + 0,71 t x .                                 (2)

- 4,28          1,90          27,77

Для оценки влияния атрибутивного признака ( u ) – «материал стен», на основе

( 1 - 0,088 построенной корреляционной матрицы Q = 0174 v 0,709 совокупный коэффициент корреляции:

- 0,088  0,174  0,709 ' 1      - 0,198  0,045 рассчитаем - 0,198     1     0,145 0,045   0,145     1 v

r*, 2 = A r„ „ + e 2 r yu 2 = ( - 0,11 ) . ( - 0,088 ) + ( 0.05 ) . ( 0,174 ) = 0,018.

Ранжирование совокупности. В исходной совокупности заменим значения атрибутивных признаков соответствующими стандартизированными коэффициентами регрессии, присваивая таким образом каждому элементу «ранг».

Таблица 1

Замена значений атрибутивных признаков стандартизированными коэффициентами

№	Стоимость квартиры, тыс. руб.	Площадь квартиры, кв. м	Материал стен		Район
			Значение атрибута	Ранг	Значение атрибута	Ранг
1	1863	48,27	Монолит	–0,11	Мясокомбинат	–0,302
2	1262	31,77	Монолит	–0,11	Мясокомбинат	–0,302
3	1010	26,01	Монолит	–0,11	Мясокомбинат	–0,302
4	1010	26,01	Монолит	–0,11	Мясокомбинат	–0,302
5	1646	42,20	Монолит	–0,11	Мясокомбинат	–0,302
6	1646	42,20	Монолит	–0,11	Мясокомбинат	–0,302
7	1545	42,70	Монолит	–0,11	Солнечный	–0,435

687	1677	36,11	Кирпич	0,00	Солнечный	–0,435
688	1531	37,91	Кирпич	0,00	Мясокомбинат	–0,302
689	2315	42,09	Панель	0,05	Иннокентьевский	0,000
763	3162	51,00	Кирпич	0,00	Взлетка	0,242
764	1100	17,60	Кирпич	0,00	БСМП	–0,012
765	3162	51,00	Кирпич	0,00	Взлетка	0,242

Теперь в рассматриваемой совокупности все признаки количественные. Получим следующее уравнение регрессии:

t_v = 0,63 t_x + 0,09 1 „ + 0,55 t_z .                               (3)

yx uz

39,92         5,93         34,95

Уравнение (3) на 81,6 % объясняет изменение цены квартир (скорректированный коэффициент детерминации составил 0,815) и с вероятностью 99 % является статистически значимым, стандартная ошибка S = 0,43.

Апробация. Аналогично проведем анализ совокупности двухкомнатных квартир (547 единиц наблюдения). В этой совокупности средняя площадь квартиры – 55,13 кв. м, средняя цена 1 кв. м – 48,41 тыс. руб., средняя стоимость квартиры – 2668,93 тыс. руб. Структура совокупности отражена на рис. 3–4.

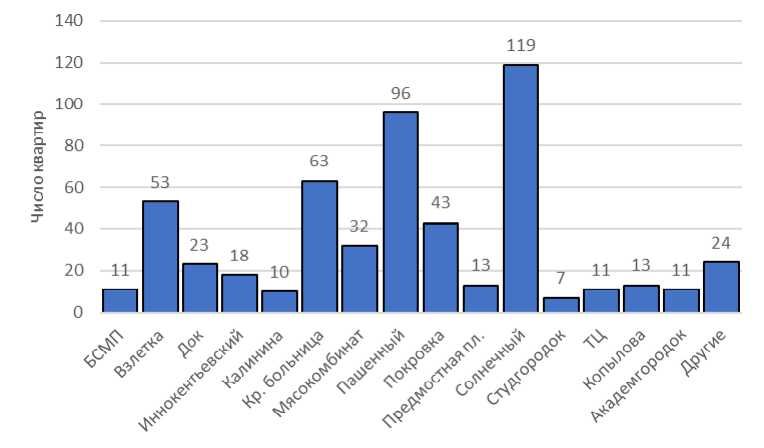
Рис. 3. Распределение предлагаемых к продаже двухкомнатных квартир по районам, г. Красноярск, 2017 г.

• Fig. 3.    Distribution of offered for sale two-room apartments by district of the city Krasnoayarsk, 2017 year

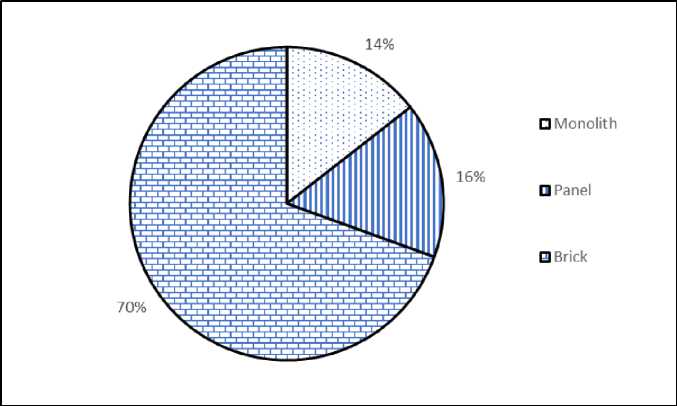
Рис. 4. Распределение предлагаемых к продаже двухкомнатных квартир по материалу стен, г. Красноярск, 2017 г.

Fig. 4. Distribution of offered for sale two-room apartments by wall material, Krasnoyarsk, 2017 year

В этой совокупности очень сильно влияние атрибутивных признаков – доля влияния атрибутивного признака в общем коэффициенте детерминации – 49,12 %. Полученное уравнение

^

t = 0,58 t — 0,02 t + 0,57 1 yxuz 30,47         — 1,24         29,31

статистически значимо с вероятностью 99 % (скорректированный коэффициент детерминации равен 0,818).

Далее проведем анализ совокупности трехкомнатных квартир (200 единиц наблюдения). В этой совокупности средняя площадь квартиры – 76,62 кв. м, средняя цена 1 кв. м – 51,05 тыс. руб., средняя стоимость квартиры – 3910,94 тыс. руб. Структура совокупности отражена на рис. 5–6.

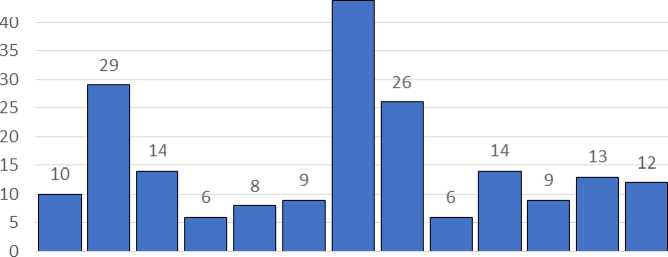
Рис. 5. Распределение предлагаемых к продаже трехкомнатных квартир по районам, г. Красноярск, 2017 г.

Fig. 5. Distribution of offered for sale three-room apartments by district of the city Krasnoayarsk, 2017 year

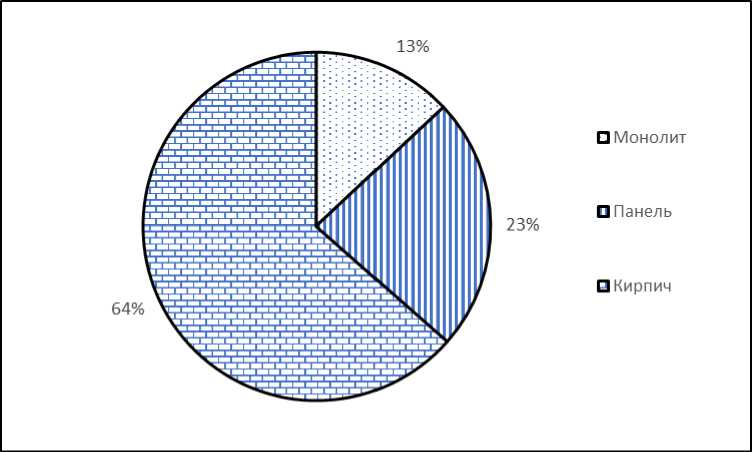
Рис. 6. Распределение предлагаемых к продаже трехкомнатных квартир по материалу стен, г. Красноярск, 2017 г.

• Fig. 6.    Distribution of offered for sale three -room apartments by wall material, Krasnoyarsk, 2017 year

По имеющимся количественным признакам ( y – стоимость квартиры, тыс. руб.; x 1 – площадь общая, кв. м; x 2 – площадь жилая, кв. м; x 3 – площадь кухни, кв. м) построим регрессионную модель в стандартизированном виде: ^

t = 0,78 1 + 0,06 1 + 0,05 1 yx x x 12,19 ¹ 1,28 ² 0,86 ³

Для этих моделей скорректированный коэффициент детерминации составил 71,4 % и уравнение регрессии статистически значимо с вероятностью 99 %. Низкие значения t -статистик говорят о том, что оценки параметров регрессии не являются статистически значимыми, а высокие значения коэффициентов корреляции между факторными признаками ( r xx 2 = 0,549; r_x 1 x ₃ = 0,648) сигнализируют о наличии мультиколлинеарности в модели. Попытаемся улучшить качество модели, добавляя атрибутивные признаки и исключая факторные признаки ( x 2 – площадь жилая, кв. м; x 3 – площадь кухни, кв. м), тесно связанные с признаком x 1 – площадь общая, кв. м.

Работая с атрибутивными признаками «материал стен» ( u ) и «район» ( z ) и количественным признаком «площадь общая» ( x ) по методике, представленной в этой статье ранее, получим стандартизированное уравнение:

t_v = 0,68 t_x + 0,01 t „ + 0,42 t_z . yxuz 24,31         0,39         14,31

Отметим, что корреляционная матрица не показывает тесной связи между факторными признаками: r xu = 0,272; r xz = 0,379; r zu = 0,390, следовательно, нет необходимости устранять мультиколлинеарность. Доля влияния атрибутивного признака в общем коэффициенте детерминации – 33,54 %. Такое уравнение является статистически значимым с вероятностью 99 % и скорректированный коэффициент детерминации составил 0,868.

Наконец, проведем анализ совокупности четырехкомнатных квартир (83 единицы наблюдения). В этой совокупности средняя площадь квартира – 107,82 кв. м, средняя цена 1 кв. м – 52,79 тыс. руб., средняя стоимость квартиры – 5692,53 тыс. руб. Структура совокупности отражена на рис. 7–8. Совокупность неоднородная (коэффициент вариации 41,2 %, преобладают квартиры в кирпичных домах).

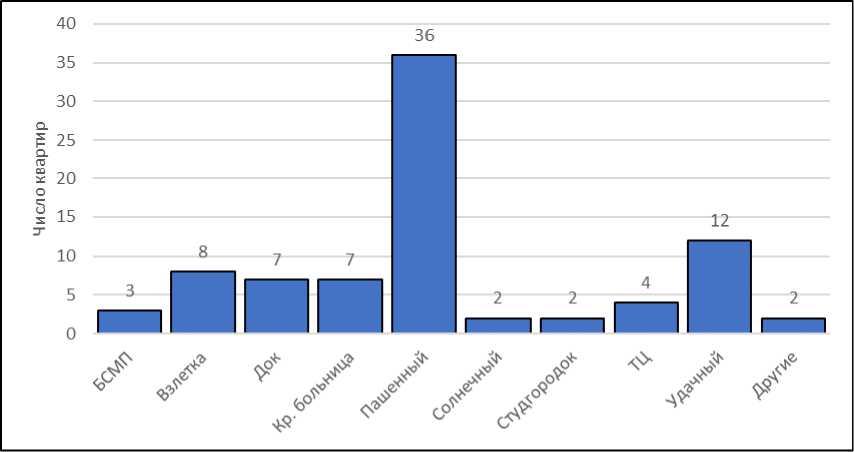
Рис. 7. Распределение предлагаемых к продаже четырехкомнатных квартир по районам, г. Красноярск, 2017 г.

• Fig. 7.    Distribution of offered for sale four-room apartments by district of the city Krasnoayarsk, 2017 year

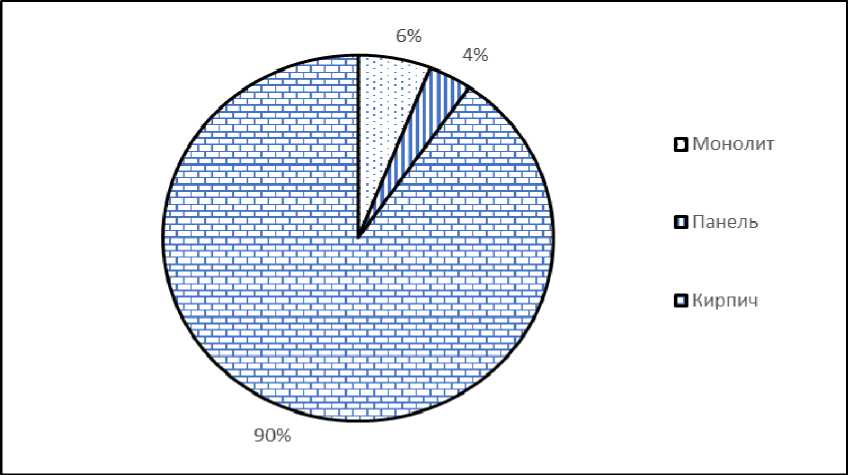
Рис. 8. Распределение предлагаемых к продаже четырехкомнатных квартир по материалу стен, г. Красноярск, 2017 г.

• Fig. 8.    Distribution of offered for sale four-room apartments by wall material, Krasnoyarsk, 2017 year

В модели, содержащей только количественные признаки, t = 1,11 t_x - 0,17 t_x yx x

18,11          - 2,74

скорректированный коэффициент детерминации составил 0,930 и уравнение регрессии статистически значимо с вероятностью 99 %.

Работая с атрибутивными признаками, получим уравнение

?_v = 0,96 t_x + 0,04 t_u + 0,001 t_z . yxuz 29,13          1,38           0,02

Заключение. Таким образом, предлагаемый метод позволяет анализировать статистические совокупности, элементы которых характеризуются и числовыми, и атрибутивными признаками. Это существенно улучшает качество моделей и учитывает большее количество факторов. Метод легко распространяется на произвольные совокупности.